特殊图类的Harmonic能量

刘海琴

(1.山西农业大学 基础部，山西 太谷 030801；2.中北大学 大数据学院，山西 太原 030051)

0 引 言

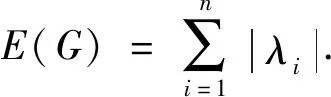
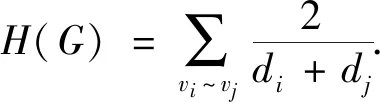
类似地，图G的Randic矩阵R(G)=(rij)n×n定义为

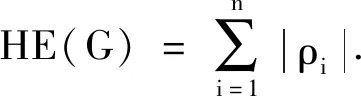
1 预备知识

下面给出路图Pn，圈图Cn，星图Sn，完全图Kn，完全二部图Km,n的具体定义.

定义1 若简单图G的顶点集为V={1,2,3,…,n}，边集为E={12,23,34,…,(n-1)n}，则简单图G称为n个顶点的路，记作Pn.

定义2 若简单图G的顶点集为V={1,2,3,…,n}(n≥3)，边集为E={12,23,34,…,(n-1)n，n1}，则简单图G称为n个顶点的圈，记作Cn.

定义3 若简单图G的顶点集为V={1,2,3,…,n}(n≥3)，边集为E={1n,2n,3n,…,(n-1)n}，则简单图G称为n个顶点的星图，记作Sn.

定义4 若简单图G的任意两个不同的顶点间恰有一条边，则此简单图称为完全图，记作Kn.

定义5 设G为简单图，若其顶点集V={1,2,3,…,n}可以分成两个互不相交的子集V1,V2，且V1中每个顶点都与V2中每个顶点相邻，则称G为完全二部图，记为Km,n,其中m=|V1|，n=|V2|.

2 路图和圈图的Harmonic特征多项式

定理1 当n≥5时，路图Pn的Harmonic特征多项式满足

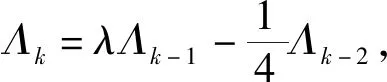
证明当k≥3时，定义

设HP(Pn,λ)=det(λI-H(Pn)),则有

HP(Pn,λ)=

将此行列式按照第一列展开可得

依次推导可得

HP(Pn,λ)=

所以

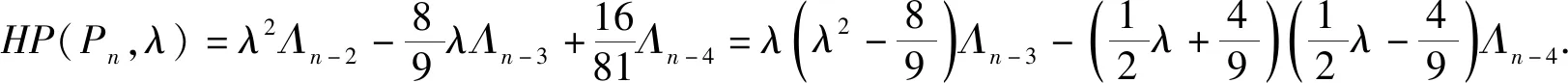
定理2 当k≥3时，圈图Cn的Harmonic特征多项式为

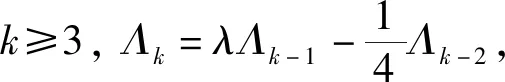
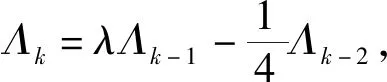
将此行列式按照第一行展开得

因此，

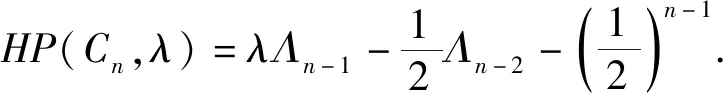
注当G是圈图Cn时，其Harmonic矩阵H(G)与Randic矩阵R(G)相等[2]，故对应特征多项式也相同.

3 星图、完全图、完全二部图的Harmonic能量的上界

对于星图Sn，完全图Kn，完全二部图Km,n，其Harmonic能量的上界均为2.下文中运用图的Harmonic特征多项式理论，给出了证明.

引理1[1]如果M是非奇异矩阵，则有

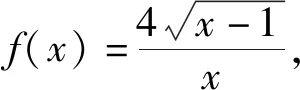
定理3 1)星图Sn=K1，n-1(n≥2)的 Harmonic 特征多项式为

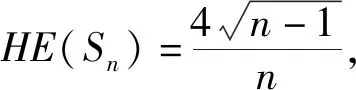
证明由于K1，n-1的Harmonic矩阵为

所以，

det(λI-H(Sn))=

由引理 1 可知，

det(λI-H(Sn))=

而

J(n-1)×1×J1×(n-1)=Jn-1,

所以，

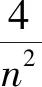
且

由引理 2 可得，当n≥2时，HE(Sn)≤2.证毕.

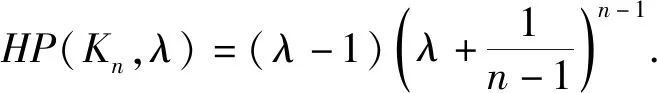
2)完全图Kn(n≥2)的Harmonic能量为HE(Kn)=2.

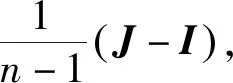
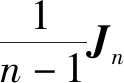
定理5 1)完全二部图Km,n(m,n≠1)的Harmonic特征多项式为

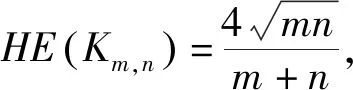
证明完全二部图Km,n的Harmonic矩阵为

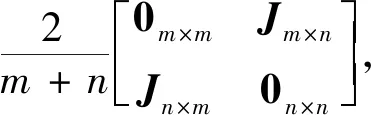
HP(Km,n,λ)=det(λI-H(Km,n))=

由引理 2 知

det(λI-H(Km,n))=

而

Jn×m×Jm×n=mJn,

则有

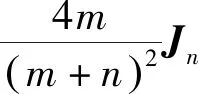
且有