融合经验共享Q 学习的粒子群优化算法

罗逸轩，刘建华+，胡任远，张冬阳，卜冠南

1.福建工程学院 计算机科学与数学学院，福州 350118

2.福建省大数据挖掘与应用技术重点实验室，福州 350118

粒子群优化算法（particle swarm optimization，PSO）是Kennedy 等受鸟群觅食行为的启发，提出的一种群体优化算法。自粒子群算法提出以来，因其易于实现和计算效率高等特点，在实际问题中得到广泛应用。但其也存在易陷入局部极小点，搜索精度不足等问题。针对这些问题，国内外学者提出参数调整、拓扑选择和与其他算法相结合等不同的改进方法。例如，文献[3-4]提出了自适应参数调整的粒子群算法，文献[5-6]通过改进拓扑结构来优化粒子群算法，文献[7-9]提出将其他优化算法（策略）与粒子群算法相结合，文献[10-11]将多种改进方法同时优化粒子群算法，以上改进均提升了粒子群算法的精度与性能。

近年来，随着强化学习发展，使用Q 学习解决粒子群算法的相关问题也逐渐受到国内外学者们的重视。Q 学习作为一种无模型的强化学习方法，具有无需环境模型的优点。因此，Q 学习与粒子群算法的结合可以应用于多种不同类型的目标函数并提升算法性能。文献[12]通过粒子群算法与强化学习相结合的方法，在噪声函数问题上取得了良好的效果。文献[13]提出了一种基于强化学习的模因粒子群优化算法，使用Q 学习帮助算法选择局部搜索策略，以提升算法的局部搜索能力。文献[14]提出了一种Q 学习的量子粒子群优化算法，将Q 学习方法用于算法的量子参数控制。文献[15]利用Q 学习的“经验”机制，定义了最佳个体的选择根据其累积绩效而不依靠每次评估中的瞬间绩效。文献[16]根据粒子群处在不同拓扑结构时搜索方式的不同，提出将Q 学习控制粒子群的拓扑结构，通过实时选择最佳的拓扑结构以提升种群的多样性。文献[17]提出一种基于Q 学习的自适应在线参数控制的粒子群算法，粒子群算法的参数决定着粒子的搜索行为，通过将粒子的参数选择作为粒子的动作，依靠Q 学习实时控制粒子参数，以此提升算法性能。

目前，将Q 学习运用到粒子群算法时，其状态、动作和奖励等参数的定义都具有主观性，若定义参数不当，不仅会使粒子缺乏灵活性，并且使Q 表无法收敛并无法有效指导粒子进行动作。在大部分结合的算法当中，仅单一地使用Q 学习来帮助粒子群算法的粒子选择动作，使得粒子过于依赖Q 学习，导致算法多样性与学习能力不足。如何将Q 学习与粒子群算法更好地结合，并且定义好参数组合，目前的文献没有进一步讨论。针对存在的问题，本文对Q 学习与粒子群结合算法的状态、动作和奖励函数进行研究与实验分析讨论，选出最优的定义参数组合，并提出了一种粒子之间经验共享的策略，形成一种融合经验共享Q 学习的粒子群优化算法（Q-learning PSO with experience sharing，QLPSOES）。对粒子均赋予一个Q 表，通过一种经验共享策略，在保持粒子自身的搜索机制之外，将粒子之间的Q 表进行了交互学习。不仅能加快Q 表的收敛，更快地学习到最优策略，也增强了粒子之间的学习能力，有利于算法在全局搜索与局部搜索当中的平衡，提升了种群的多样性与粒子群算法的性能。

1 相关知识介绍

1.1 粒子群算法

粒子群算法是一种群体智能算法。在粒子群中，个体（粒子）通过搜索多维问题解空间，在每一轮迭代过程中评价自身的位置信息（适应度值）。在整个粒子群搜索过程中，粒子共享它们“最优”位置信息，并且受到自身先前最优解的影响来调整它们自己的速度和位置。假设在维搜索空间中，粒子的速度和位置更新公式如式（1）和式（2）所示。

1.2 Q 学习方法

Q 学习方法（Q-learning）是由Watkins 等人提出的一种无模型的强化学习方法，其主要思想是通过智能体与环境的不断交互，并累计最大回报以得到最优的策略。Q 学习主要组成如图1 所示。Q 学习拥有一个可以指导智能体选择具有最大Q 值即最优动作的Q 表，其更新公式为：

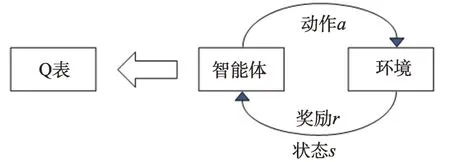
图1 Q 学习主要组成Fig.1 Composition of Q-learning

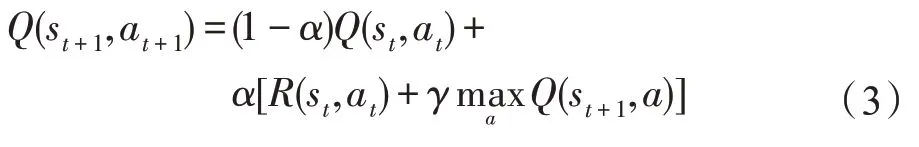
式中，s、s与a、a分别是第代与+1 代时的状态与动作；和分别是学习率和折扣系数，并且都在[0,1]内。(s,a)是智能体在状态s下执行动作a所获得的即时奖励，(s,a)是智能体在状态s采取动作a的期望Q 值。

1.3 QLSOPSO 算法原理

QLSOPSO（Q-learning-based single-objective particle swarm optimization）算法是一种基于Q 学习的粒子群优化算法。如图2 所示，将粒子群算法的粒子群当作Q 学习中的智能体，通过一系列的定义，能够使Q 学习对粒子群进行自适应的参数控制，以提升粒子群算法的性能。

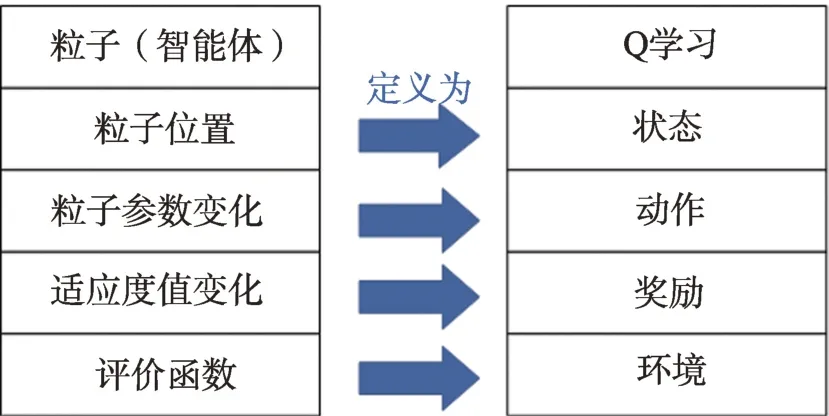
图2 QL 与PSO 算法的关系Fig.2 Correspondence between QL and PSO

该算法设计了一个三维Q 表，如图3 所示，它由粒子的状态平面与动作列组成。粒子的状态平面包括决策空间状态与目标空间状态，动作列设置不同动作参数用于控制粒子的探索与开发。其中，粒子的位置与全局最佳位置之间欧几里德距离（与搜索空间的大小相比）作为决策空间的状态，如图4 所示，可以将其分为四种状态：{最近，更近，更远，最远}。粒子与全局最佳适应度值和全局最差适应度值之差的相对性能作为目标空间的状态，如图5 所示，可以将其四等分为{适应度值大，适应度较大，适应度较小，适应度值小}。

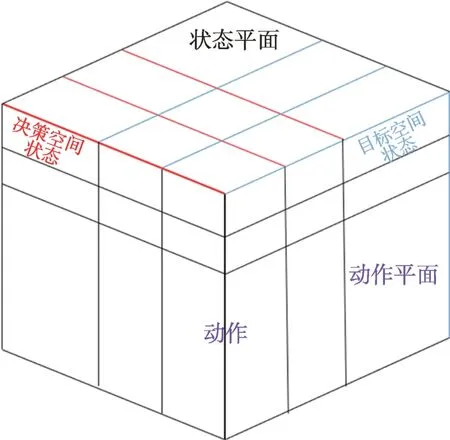
图3 三维Q 表Fig.3 3-D Q table

图4 决策空间状态Fig.4 Decision space state

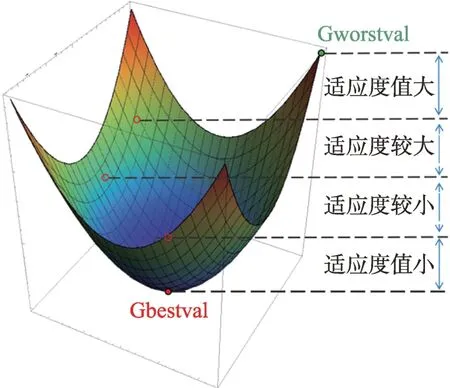
图5 目标空间状态Fig.5 Objective space state

该算法通过自适应的参数控制，一定程度上提升了算法的性能，但其存在粒子的动作参数选择不合理与Q 表收敛速度较快等问题，其定义见第2 章。

2 融合经验共享Q 学习的粒子群算法

在QLSOPSO 算法中，粒子的动作参数存在着主观性选择问题，其会导致算法的收敛性能不佳；并且所有粒子仅共享一个Q 表，使得Q 表收敛过快。针对其存在的问题，本文首先确定合适的粒子动作定义，提出将每个粒子均赋予一个Q 表，作为粒子“经验”，并设计一种经验共享的策略，即一种Q 表的交互方式，使粒子之间的信息有更多的交流。粒子的动作定义有助于粒子做出最优的行为；单个粒子的Q 表有利于粒子的局部搜索；经验共享策略增强了粒子的全局搜索能力，以改进算法的搜索性能。

2.1 粒子的动作定义

在图3 的Q 表中，粒子动作是控制粒子在不同状态下选择最合适的搜索行为。因此，动作的定义至关重要，主要由三个参数影响，分别为、和。为惯性权重，和为加速度系数，这三个参数会影响粒子的搜索行为，以决定粒子的探索与开发。决定粒子对当前速度继承性，越大，全局搜索能力越强，越小，局部搜索能力越强。同样地，设置较大的，有助于增强全局搜索，而较大的，会促使粒子收敛。

因此本文算法中设置三种动作行为，使其符合粒子的搜索行为，将粒子的动作分为三类：{全局探索（），综合搜索（），局部开发（）}。每一种动作会对应着不同的动作参数。通过对动作的不同选择，得到粒子群算法的不同参数，实现对粒子的搜索控制，从而改变粒子的飞行行为。设置方法如表1 所示，而参数的具体设置值在第3章的实验分析中得出。

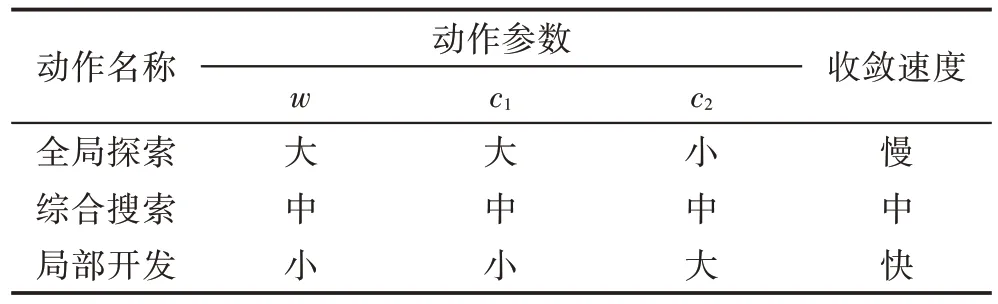
表1 动作Table 1 Action

2.2 单个粒子的Q 表

三维Q 表由状态平面与动作组成，如图3 所示，其状态平面由决策空间状态和目标空间状态组成。如图4，决策状态空间由粒子之间的相对距离衡量，反映了粒子的收敛状态。如图5，目标状态空间由粒子适应度值衡量，直接反映了粒子的性能。如表1 所示，动作决定了粒子的算法参数组合。综上所述，Q表的状态平面能够直观反映粒子所处的空间环境状态，而通过奖励函数更新后的Q 表，可以帮助粒子根据其状态来决定粒子的参数，因此Q 表对粒子的行为有着至关重要的影响。

本文提出将单个粒子赋予一个独立的三维Q 表，如图6 所示。若粒子群仅更新一个Q 表，Q 表的更新会受到每一个粒子的影响，使得Q 表的更新不稳定和收敛速度过快，且不能反映每一个粒子的之前的状态。单个粒子的Q 表设计，使得每一个粒子均成为“智能体”对环境进行探索。在算法前期通过粒子探索并存储单独的“经验”，而在算法后期再利用Q 表，能对搜索环境得到一个良好的反馈，从而更加准确帮助粒子确定合适的参数，调节种群的全局与局部搜索能力。

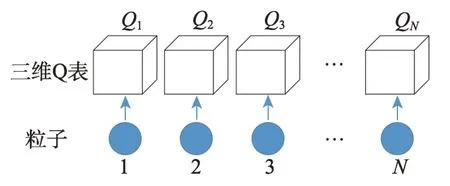
图6 每个粒子均赋予Q 表Fig.6 Q table of each particle

2.3 粒子之间的经验共享策略

粒子群算法通过改进粒子之间交互方式能够提升算法的性能，因此，本文设计一种学习经验共享策略，使得粒子之间具有更强的交互性。由于粒子均拥有一个Q 表，在迭代的过程中，可以将每个粒子的“行为经验”存储，而将当前最优位置粒子的Q 表作为“最优Q 表”。在粒子更新Q 表时，将作为“学习”对象，通过最优Q 表的“经验”更新粒子本身的Q 表，以达到经验共享。其步骤示意图如图7 所示。

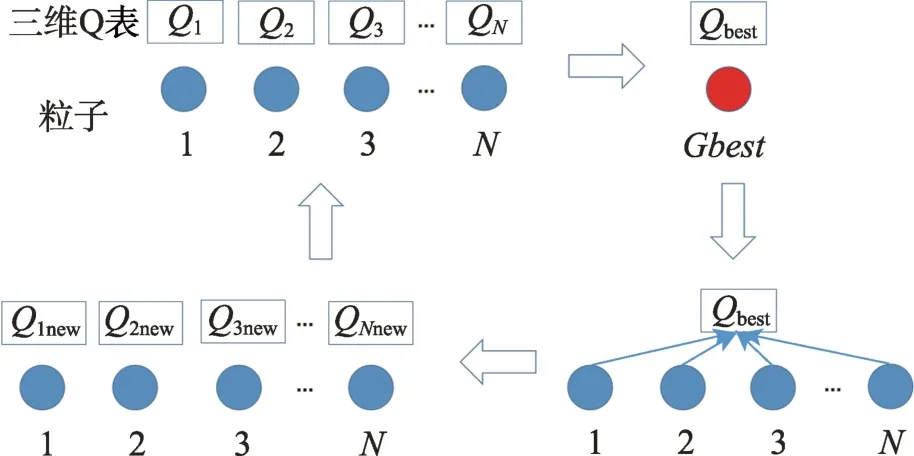
图7 经验共享策略Fig.7 Experience sharing strategy

通过共享策略，粒子之间的交流通信更像人类社会中人与人之间的相互学习、并向更优秀的人学习的学习方式。通过Q 表的交互，有利于Q 表的收敛。同时粒子保留自身的经验并能学习最优解粒子的策略，提升了种群的局部搜索能力与收敛于最优解的可能性。

2.4 QLPSOES 算法框架

算法具体伪代码如下：

输入：种群、最大迭代次数。

输出：最后一代全局最优解的适应度值。

算法的框图如图8 所示。

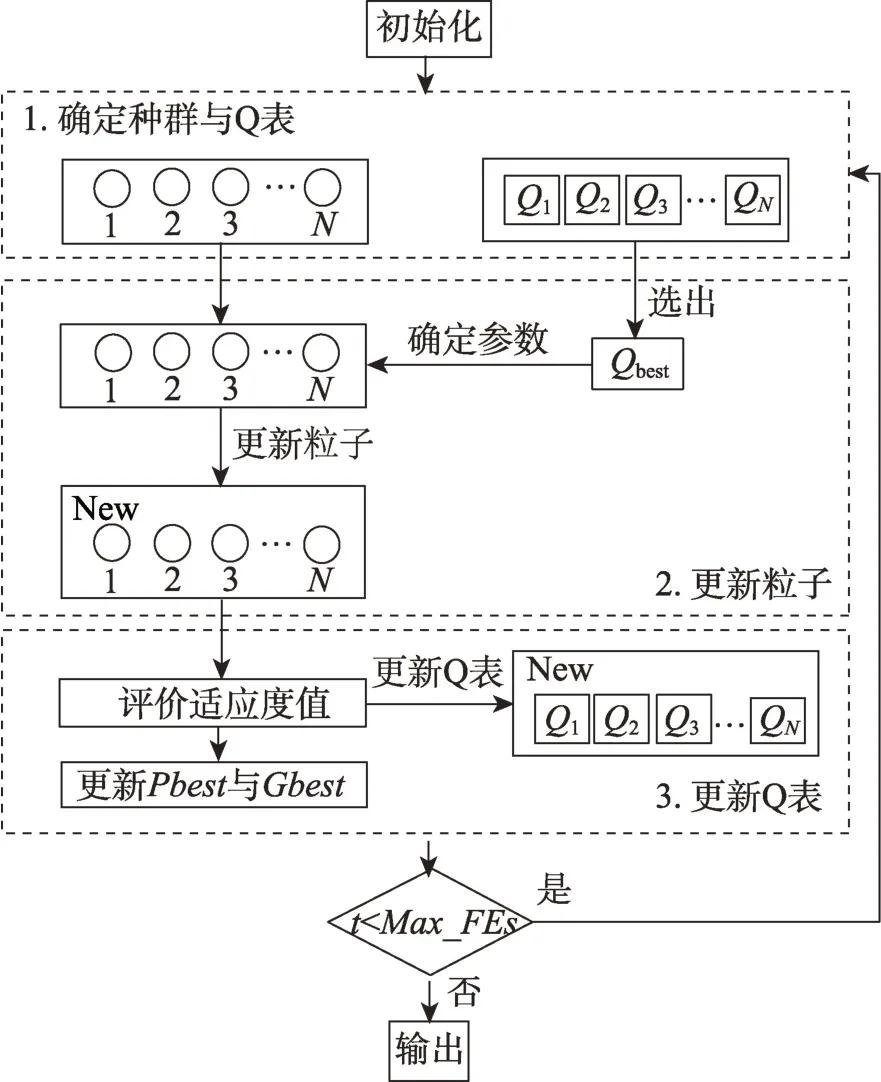
图8 QLPSOES 算法框架Fig.8 Framework of QLPSOES

2.5 时间复杂度分析

由QLPSOES 算法流程可知，其主要包括如下部分：（1）初始化，时间复杂度为(×)；（2）决定粒子的状态、动作与参数的时间复杂度均为(_×)；（3）粒子进行速度与位置的更新，时间复杂度为(_××)；（4）计算粒子适应度值，更新个体最优及全局最优的时间复杂度为(_××) ；（5）更新Q 表的时间复杂度为(_×)；（6）判断迭代是否停止的时间复杂度为(1)。因此，算法的时间复杂度为(_××)，与标准粒子群算法的时间复杂度保持相同。

3 QLPSOES 参数实验分析

在Q 学习与粒子群算法结合时，Q 学习的状态、动作和奖励函数等要素的确定对算法有着显著的影响。因此，粒子的状态、动作参数该如何设定，使其更加符合粒子的“行为”；奖励函数该如何设置，使其更加符合算法的收敛方式等。但是，目前文献对这些要素的设置带有主观性选择与盲目优化等问题，没有对该问题进行实验分析。本章通过实验方法，分析QLPSOES 中三种定义对算法的影响，并采用正交设计法对三个定义进行方案选择。通过CEC2013测试函数评判不同参数的好坏，以确定最优的参数组合。

3.1 实验设计方法

本文采用CEC2013 测试集中的28 个基准函数进行实验分析，28 个函数具体信息如表2 所示。其中1～5 为单峰函数，6～20 为多峰函数，21～28 为复杂函数，不同类型的函数有助于更全面更广泛地测试算法性能。在每一个维度的搜索范围均为[-100,100]。其中，种群规模设置为30，维度设置为10维，最大迭代次数设置为50 000，每种算法测试函数运行次数设置为30 次。

表2 CEC2013 测试函数Table 2 CEC2013 benchmark functions

3.2 实验中三个定义的备选方案

根据上文中的定义，粒子与在不同的相对距离时，决策状态能够帮助粒子选择最优动作。例如，在算法运行后期，若粒子与相距过远，决策状态就能使粒子选择收敛的动作参数。本小节分析实验确定了三种决策空间状态，分别命名为决策空间状态Ⅰ、决策空间状态Ⅱ、决策空间状态Ⅲ，其详细划分如表3 所示。表示粒子与全局最佳位置之间的欧几里德距离，Δ表示决策空间的范围，是指决策空间的上限和下限之差。

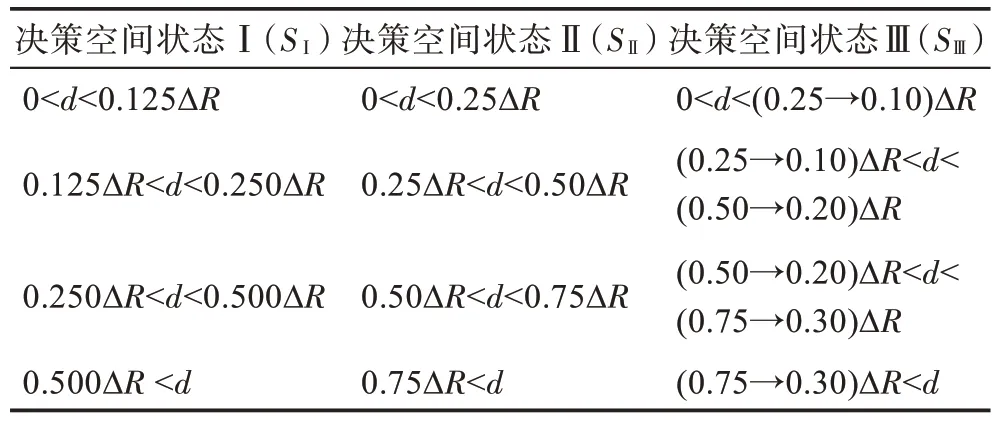
表3 决策空间状态参数设置Table 3 Setting of decision space state parameters

在粒子群算法当中，参数的设定对于算法性能有着较大的影响。许多学者对其的设定进行了研究与分析，例如，文献[3]推荐为固定的参数值，文献[23]提出惯性权重随迭代次数线性减少的策略，文献[24]提出线性递减、线性递增的策略。以上参数方案都提高了算法的性能。但在QLPSOES 算法中，动作是离散的，粒子的参数变化需以离散的形式表示，因此无法直接与连续的参数变化对应，需要选择合适的动作参数组合使得粒子做出的动作更好地符合实际的需求，以达到探索和开发的目的。本小节实验中设置了三种动作参数组合，详细的动作参数组合设置如表4 所示。

表4 动作参数设置Table 4 Setting of action parameters

在强化学习当中，奖励函数起到引导智能体学习方向的作用，若缺乏奖励信息会导致智能体学习进度缓慢甚至无法学习到最优策略。同样，粒子群算法与强化学习结合过程中，奖励函数的设定也十分重要。例如，文献[13，16]都提出不同的设定方法。本小节实验设置了三种奖励函数，详细的奖励函数设置如表5 所示。其中，代表适应度，代表位置多样性函数，为迭代次数，代表动作行为。

表5 奖励函数Table 5 Reward functions

3.3 参数设置实验分析

正交实验设计是针对多因素多水平问题的设计方法，其借助于一种规格化的正交表来用部分实验代替全面实验。正交实验设计具有实验次数少、分析方法简单等优点，能够通过代表性的少数实验找出最佳的参数组合。一个三因素三水平的实验，若采用完全实验方案，则共需要3=27 次的组合实验。而利用正交表，只需做9 次实验就能够反映实际情况，充分提高了实验的效率。正交实验方法作为一种高效处理多因素优化问题的科学计算方法，已经广泛应用于工业生产及科学研究。

本小节采用正交实验方法，具体步骤如下：

确定影响因素与因素水平。根据上文分析，主要影响算法性能的因素分别为粒子的决策空间状态、动作参数和奖励函数。将这三个参数设定为正交设计实验的三个因素，并分别对应因素1、因素2 和因素3，每一个因素有三个水平。其QLPSOES参数因素水平如表6 所示。

表6 参数因素水平表Table 6 Factors and levels of parameters

设计正交实验表。SPSS（statistical product and service solutions）是一款用于数据管理和数据分析的软件，因此本文运用SPSS23.0 进行正交实验表的设计与分析。

制定实验方案并实验。根据SPSS 设计的正交表，本文制定九种实验方案且不考虑各因素间的交互作用。按照表6 中不同参数组合的实验方案进行实验，运行环境参数设置同3.1 节的情况，评价指标为CEC2013 中28 个测试函数Friedman 检验的rank 得分。实验结果如表7 所示。

表7 正交方案与实验结果Table 7 Orthogonal experiment and results

实验结果分析。本文将通过极差分析法和方差分析法对实验结果进行分析。极差分析法可以直观形象地分析主次因素和最优组合等，方差分析法能更精细地分析各因素对结果的影响程度。

首先，利用极差分析法对实验结果进行分析，根据极差值可以确定因素的主次地位。极差分析结果如表8 所示，其中值代表极差值，值反映因素对结果的影响程度，值越大代表影响程度越大。从表8 可以看出，因素1 的值为0.573 3，因素2 的值为4.480 0，因素3 的值为0.883 3。因此动作参数对算法影响较大。三个因素对结果影响程度从大到小依次是动作参数、奖励函数和决策状态空间。rank 的评价指标是平均值误差，因此rank 值越小代表参数组合的性能越优。并通过极差分析法的指标，得出了初步最优组合为。

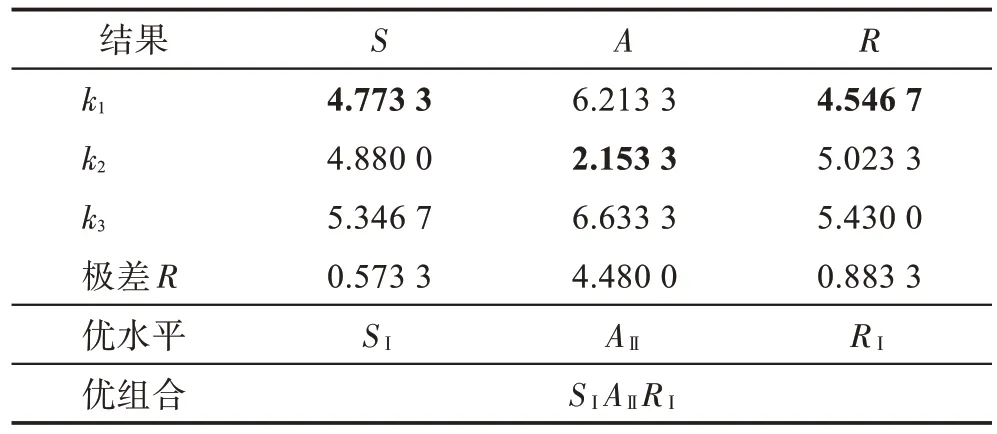
表8 极差分析表Table 8 Range analysis

同时，也采用方差方法分析实验结果，方差分析结果如表9 所示。表9 代表的是主体间效应的检验，其中值反映因素对结果的影响程度，值越大，因素对结果的影响程度越大；.是因素的显著性水平，显著性水平越小，代表其因素对结果的影响程度越大。根据表9 数据，QLPSOES 算法的参数影响排名从大到小为动作参数、奖励函数和决策状态空间。方差分析与极差分析得出的排名一致。动作参数的.小于0.05，代表动作参数会对算法性能产生显著性影响。通过上述实验结果可得，最优组合为，最终参数组合如表10 所示。

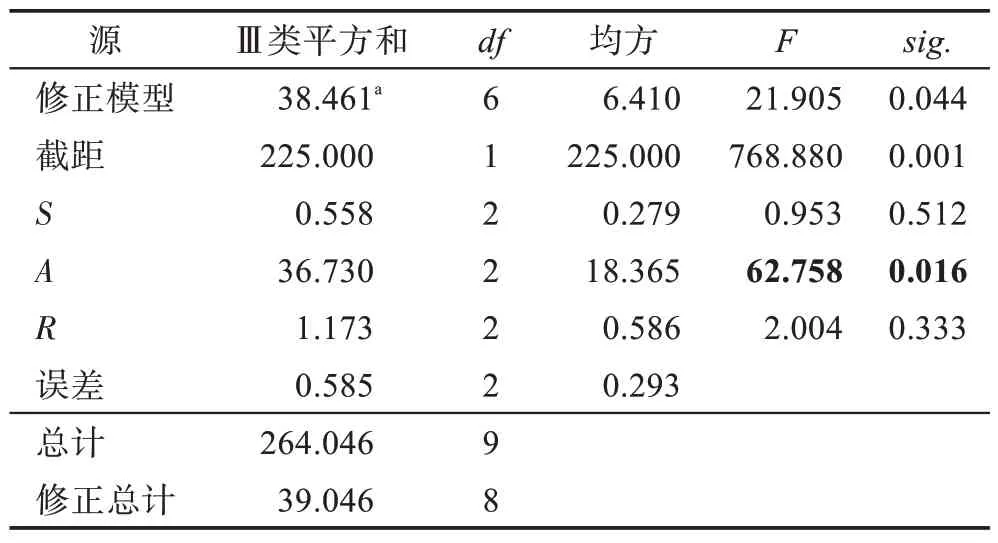
表9 主体间效应的检验（因变量：rank）Table 9 Test of intersubjective effect(rank)

表10 QLPSOES 参数组合Table 10 Parameters of QLPSOES

4 QLPSOES 算法的实验与比较

第3 章通过实验分析选取最优参数组之后，为了分析比较本文算法的有效性和适用性，本章选取CEC2013 中的28 个标准测试函数进行比较实验，将本文算法与其他Q 学习结合的粒子群算法（QLPSO-1D、QLPSO-2D、QLSOPSO）、HPSO（hybrid PSO with topological time-varying and search disturbance）和HCPSO（particle swarm optimization based on hierarchical autonomous learning）进行对比实验。这些算法的参数均采用其原始论文中的参数设置，实验的参数设置如表11 所示。

表11 实验的参数设置Table 11 Parameter setting for experiment

4.1 算法的精确性分析

表12 展示了6 种算法在28 个测试函数中的平均适应度值，表13 展示了各算法通过Friedman 检验对比的排名。从表12 可以看出，QLPSOES 算法在函数8、11、14、16、18、21、22、25、28 共9 个函数中获得最优的平均适应度值。结合表13 各算法的秩均值，QLPSOES 以2.55 的平均排名获得了最佳的综合性能。

表12 函数测试实验结果Table 12 Experimental results of function test

表13 算法的弗里德曼检测与时间复杂度比较Table 13 Friedman test and time complexity comparison of algorithms

在多 峰函数中，QLPSOES 算法在8、11、14、16、18 中获得最佳适应度值，同时，QLPSOES 算法在多峰函数的rank 排名第二，证明其在多峰函数中有着较好的优化效果。而在单峰函数中，QLPSOES并没有获得最优的适应度值，并从Friedman 检验可以看出，QLPSOES 的排名为第二，说明QLPSOES 算法在单峰函数中收敛情况一般。

针对复杂函数，QLPSOES 算法在8 个复杂函数中取得4 个最佳适应度值，且在函数23、24 中的收敛性能与最优算法差距较小，有着较好的收敛能力。结合Friedman 检验可以看出，QLPSOES 算法处理复杂函数的问题的排名明显优于其他对比算法，获得了最佳的综合表现，证明了该算法处理复杂函数的优越性。表13 同时给出各算法的时间复杂度，QLPSOES 算法在与标准粒子群算法持平的复杂度中取得较好的效果。

4.2 收敛性分析

图9 是各个算法在部分测试函数中的收敛情况，各在3 种类型的测试函数中选取两个函数，以表现算法在不同函数模型下的收敛情况。

从图9（a）和图9（b）可以看出，QLPSOES 算法在2、4 即单峰函数中与其他算法的收敛速度与收敛精度相当。从图9（d）和图9（e）看出，算法在18、23 上都只需较少的迭代次数就能找到全局最优解，有着较快的收敛速度。从图9（c）和图9（f）看出，算法不仅前期收敛曲线下降速度快，且在后期也具备一定的寻优能力，且其精度更高。综合看来，QLPSOES 算法在多峰与复杂函数中较其他算法具有更优的收敛性能。

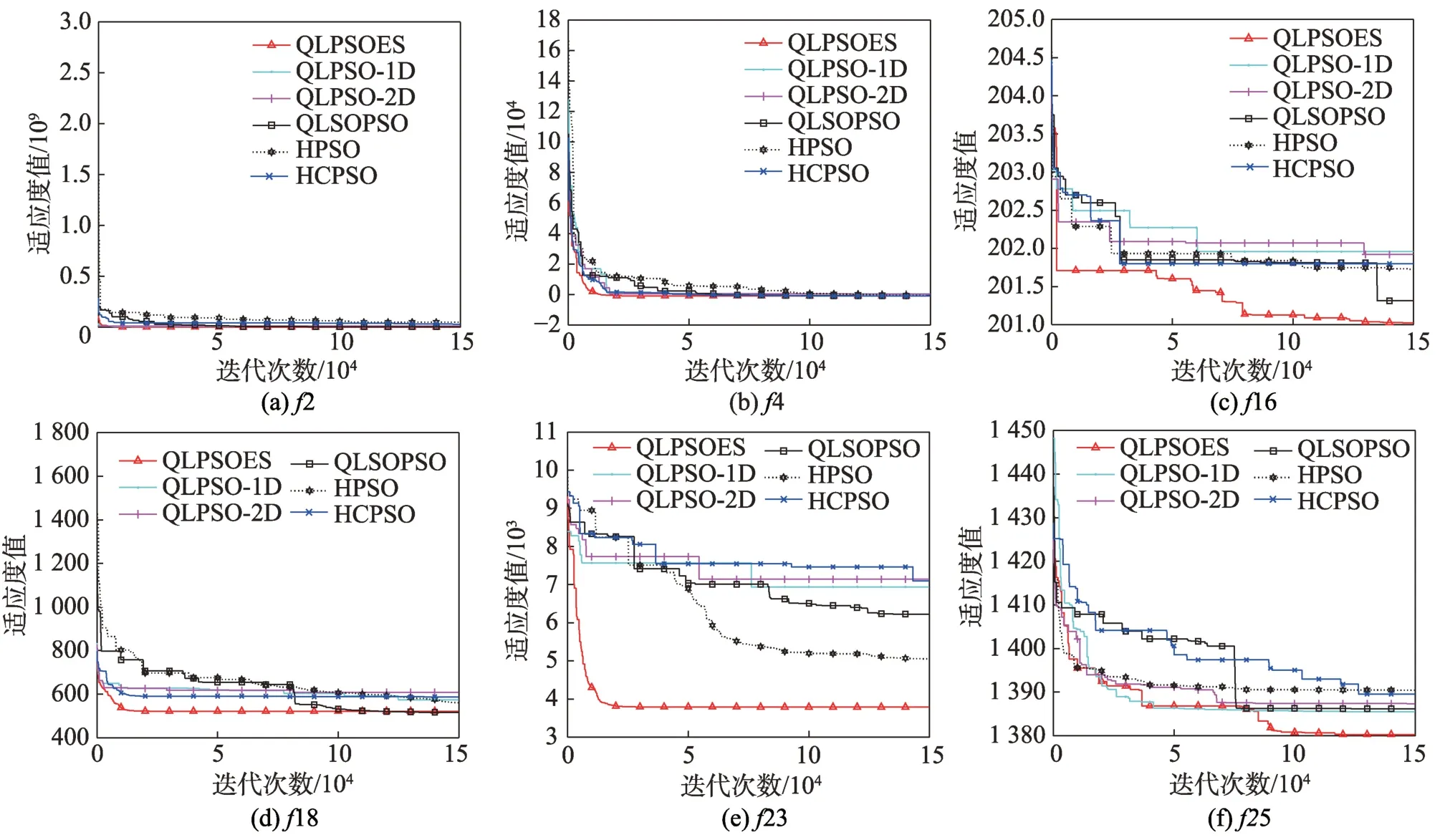
图9 六个测试函数的收敛曲线Fig.9 Convergence curves of six test functions

4.3 策略的有效性分析

本文提出将每个粒子均构建Q 表，并通过Q 表进行经验共享。为了进一步验证策略的有效性，本文对QLPSOES 算法及其两种变体QLPSO-A 和QLPSO-B进行比较，算法的具体设置如表14 所示。

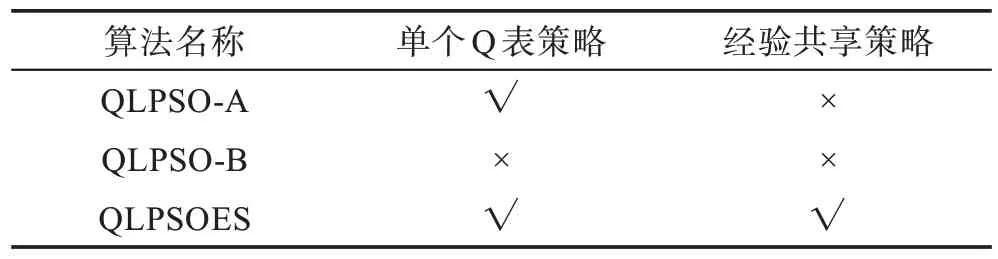
表14 对比算法的策略设置Table 14 Strategy setting of algorithms

为了更加直观地反映策略对算法的影响，以25为例，对三种算法进行比较。图10 是三个算法的种群动作数量变化图，其通过种群中的动作数量分布反映整个种群的搜索状态。图10（b）所示的QLPSOB 算法中，粒子仅更新一张Q 表，Q 表会快速收敛，使得种群在一定的迭代次数中，做出长时间相同的“动作”；前期几乎只做出探索的动作，而后期只做收敛的动作，导致前期收敛能力与后期的探索能力不足，容易陷入局部最优解。图10（a）所示的QLPSO-A 算法，相比仅更新一张Q 表，单个粒子的Q 表前期不易收敛，粒子的更新不依赖于Q 表，其会以原先的更新公式更新速度与位置，使其种群中的动作类型丰富，证明了单个Q 表的设计能够提升粒子的探索与勘探能力。但在Q 表收敛以后，也存在相同的种群缺乏动作类型的问题。

从图10（c）可以看出，加上经验共享策略后种群的动作数量变化更为平滑，提升了粒子动态参数选择的准确性。通过粒子的参数自适应变化，做全局搜索的粒子总体呈现随迭代次数减少，做局部搜索的粒子随迭代次数增加，符合前期探索、后期收敛的策略。种群在保证收敛的同时，保留部分粒子探索，有效地平衡了粒子全局搜索与局部搜索能力。

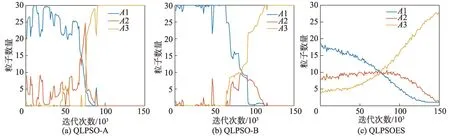
图10 种群动作数量Fig.10 Number of population actions

种群多样性不足是粒子群算法易陷入局部最优点的主要原因。为了体现种群位置多样性的变化情况，以23 和25 为例，将QLPSOES 与其变体和PSO 进行位置多样性对比。图11 给出了4 种算法的位置多样性的变化曲线。

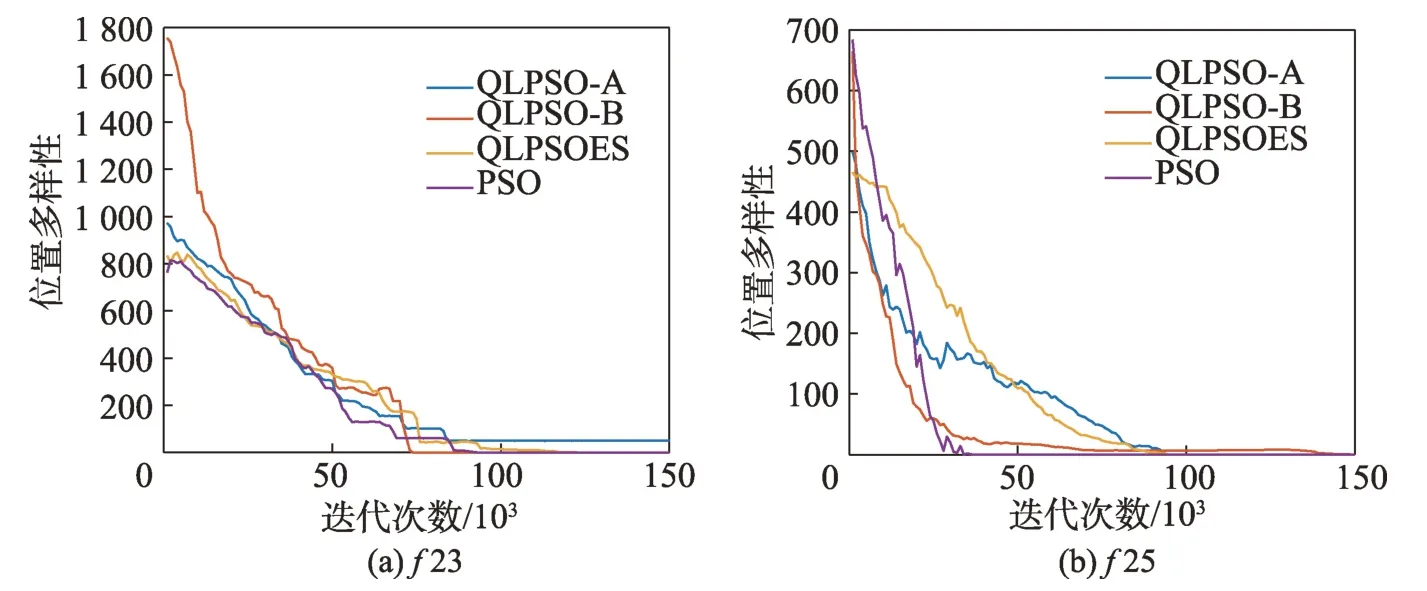
图11 位置多样性Fig.11 Position variety

从图11 可以看出，PSO 算法的多样性相比其他算法，在迭代初期就已呈现聚集状态。QLPSO-B 的种群多样性的初始范围相对较大，但收敛速度仍较快，不利于全局搜索。相比QLPSO-B，QLPSO-A 与QLPSOES 算法前期多样性的范围不大，但其变化较为稳定，粒子分布均匀，保持较强的探索能力。说明了单个Q 表的策略有利于保持算法的全局搜索能力。但在迭代后期，QLPSO-A 最终的收敛时间较长，不利于算法的局部搜索。QLPSOES 算法加上了经验共享策略，在中后期加速了粒子的收敛，提升算法中后期种群局部搜索的效果。

综上所述，在迭代前期，单个Q 表的策略有助于粒子的探索，粒子通过自身运动并累积“经验”，使得全局搜索能力较强，保持种群多样性；在迭代后期，累积经验后的Q 表通过经验共享策略，帮助粒子依据Q 表状态选择最佳参数，提升了局部搜索能力，提高了收敛精度。QLPSOES 能够在复杂函数取得较好的优化效果的原因在于两种策略的共同作用，其有利于平衡种群的全局探索和局部探索能力，种群在收敛的同时保持探索，避免了算法陷入局部最优。

5 结束语

本文针对传统粒子群算法易陷入局部与多样性不足等问题，提出了一种基于Q 学习且具有经验共享策略粒子群优化算法。首先利用Q 学习方法，通过每一个粒子赋予的Q 表帮助粒子进行参数选择，提高了种群多样性与全局搜索能力。其次，引入学习经验共享策略，通过强化学习中的“经验”机制，增强了粒子之间的学习能力，提升了种群的局部搜索能力。通过正交实验方法，确定了Q 学习方法运用到粒子群算法当中的主观性参数问题，提升了算法的性能。在CEC2013 测试函数中，与其他多种变体粒子群算法进行比较，验证了算法的有效性。在未来的工作中，将研究如何将强化学习与其他的进化算法相结合，进一步地提升算法性能。