柯西中值定理各元素分析及函数图形验证

◎郭 嘉 （集美大学航海学院，福建 厦门 361021）

1 引 言

罗尔定理、拉格朗日中值定理、柯西中值定理统称为微分学基本定理，它们应用广泛而又相互联系.柯西中值定理是高等数学中最主要的定理之一，关于它的证明，可通过采用利用辅助函数的方法，并利用罗尔定理来证明.其证明中的难点在于构造辅助函数.柯西中值定理相对于拉格朗日中值定理更为抽象，部分初学者中不易掌握参数方程及辅助函数，对柯西中值定理没有透彻地理解掌握，做题时也不能灵活应用.这点教学教师也深有体会：“在微分中值定理的教学中，应用其有效的几何现象，通过几何图形直观深入地探讨其理论内涵，并通过实例来说明定理的条件、结论、几何解释以及各定理间的联系和应用，特别是柯西中值定理在教材中没有举例说明，学生对参数曲线的柯西中值定理难以理解.”造成了学生在初学时对柯西中值定理的证明不易从原理上理解、掌握，有的学生只能通过死记硬背记住了“辅助函数”，以应对可能考出来的证明柯西中值定理题目.为了初学者能够透彻地掌握柯西中值定理，下面就从构成定理的每一个元素的坐标系、来源、作用、意义入手来分析定理.

2 柯西中值定理中的f（x），F（x），x，ξ四者的坐标系分析

2.1 拉格朗日中值定理元素分析

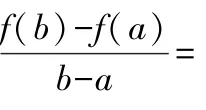
拉格朗日中值定理的6个元素，，，（），（），（）都在一个坐标系内，，，同属于自变量的范围，即属于坐标系的横轴；（），（），（）属于坐标系的纵轴.

2.2 柯西中值定理元素分析

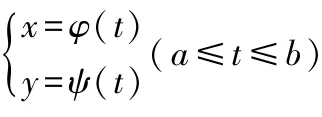
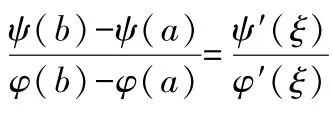
同时，3个坐标系的数据又是相互关联的，即，坐标系中，的值分别来自，坐标系及，坐标系.

2.3 利用拉格朗日中值定理推演柯西中值定理

建立新的坐标系，横坐标为，即（），纵坐标为，即（）.在［，］区间，根据拉格朗日中值定理（）-（）＝（）（-）可知，

2.3.1 中值定理式中的（），（）分别为新坐标系的（），（）.

2.3.2 中值定理式中的，分别为新坐标系的（），（）.

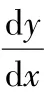
2.4 对于柯西中值定理，应建立以下三个概念

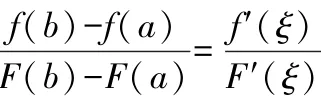
2.4.2（），（）分别对应于参数方程的（），（），（），（）分别对应于参数方程的（），（），不可把几个关系混淆，特别不可把，，，与混淆.

2.4.3（），（）在同一坐标系内，，在同一坐标系内，此时的等同于

3 用函数图形及实例函数验证柯西中值定理

教材在讲述和证明拉格朗日中值定理时，以图形的形式予以了说明，而讲述柯西中值定理时，没有使用图形，这就造成了从几何意义和物理意义理解柯西中值定理有了困难.为了更好地理解柯西中值定理，这里先把拉格朗日中值定理的几何意义、物理意义及图形简单表述一下.

3.1 拉格朗日中值定理的几何意义及物理意义

3.1.1 拉格朗日中值定理的几何意义

若连续曲线＝（）在（，（）），（，（））两点间的每一点处都有不垂直于轴的切线，则曲线在、间至少存在一点（，（）），使得该曲线在点的切线与割线平行，如图1所示.

图1 拉格朗日中值定理几何意义图Fig.1 The geometric meaning of Lagrange′s mean value theorem

3.1.2 拉格朗日中值定理的物理意义

3.2 用图形分析柯西中值定理

根据上部分叙述，要从图形上理解柯西中值定理，需要在3个坐标系内画图，即（1）在，坐标系画出，（）图形，（2）在，坐标系画出，（）图形，（3）在，坐标系画出（），（）图形.

用拉格朗日中值定理图形变换后的柯西中值定理图形：

根据上文“2.3”表述，将拉格朗日中值定理原图形中的，分别用（），（）代替；（），（）分别用（），（）代替；坐标轴，分别用（），（）代替；横坐标用（）代替，，，点的坐标分别为（（），（）），（（），（）），（（），（）），柯西中值定理的几何图形如图2所示.

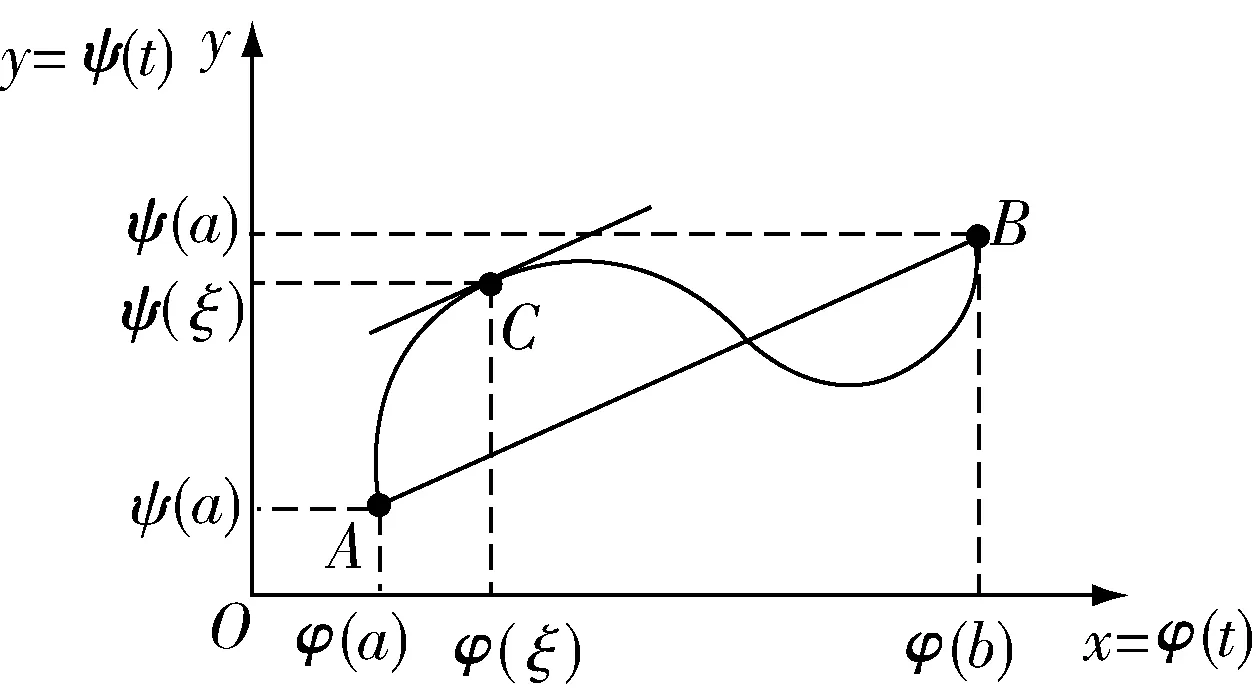
图2 柯西中值定理几何意义图Fig.2 Cauchy mean value theorem geometric meaning diagram

教材中柯西中值定理中的（），（）分别对应于参数方程的（），（），（），（）分别对应于参数方程的（），（）.

3.3 用一个实例函数图形来进一步分析验证柯西中值定理

3.3.1 建立实例函数：

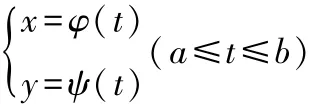
取两个常见的函数：

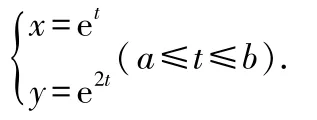
2）与参数方程等价的普通方程：＝.

3）参数方程分别对求导：

（）＝e，（）＝2e.

3.3.2 取值并验证

令＝0，＝5，则（0）＝1，（5）＝e，

（0）＝1，（5）＝e 10.

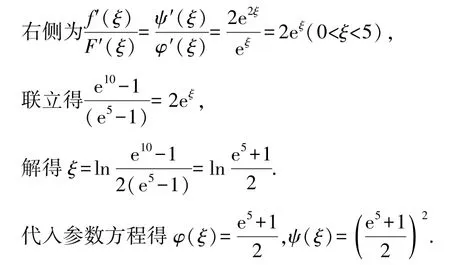
3.3.3 分别画出3个函数的图形（注：为了有效展示图形走势，轴、轴数值比例不等于1：1），如图3、图4、图5所示.

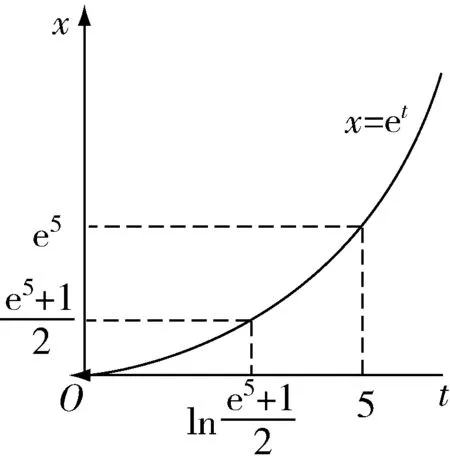
图3 参数方程x＝et图形Fig.3 Parametric equation x＝et graph

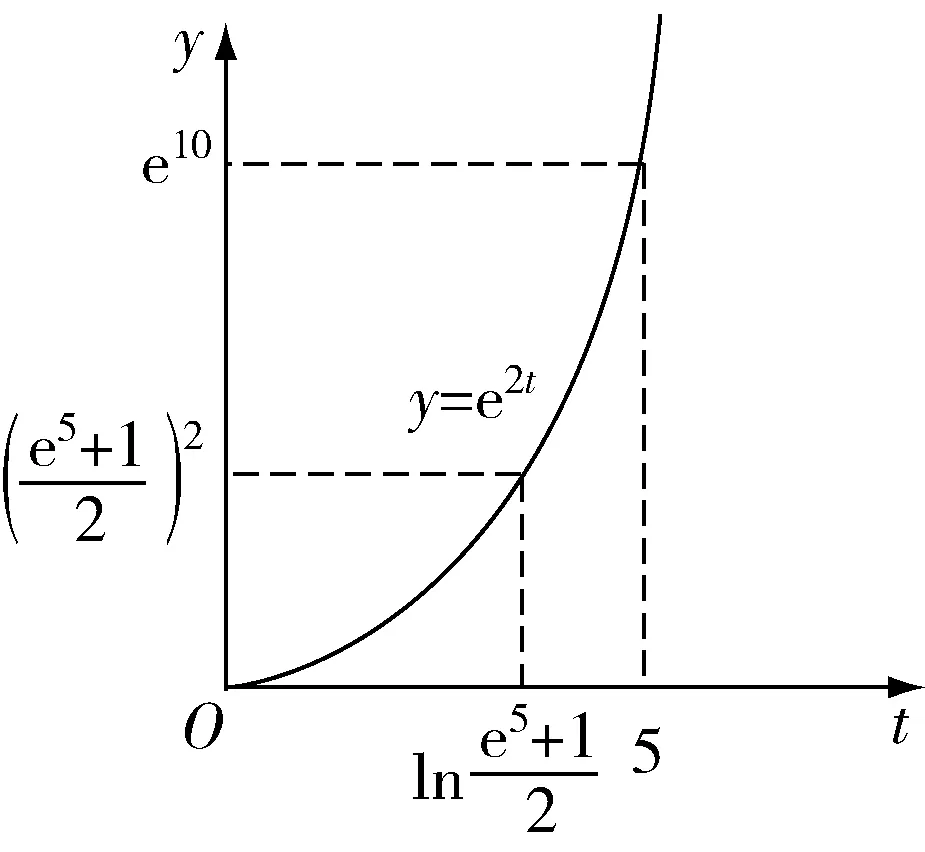
图4 参数方程y＝e2t图形Fig.4 Parametric equation x＝e2t graph

图5 与参数方程等价的普通方程图形Fig.5 Graphs of ordinary equations equivalent to parametric equations

4 并不一定存在同一个ξ，使得拉格朗日中值定理在两个参数方程及与参数方程等价的普通方程中同时成立

初学柯西中值定理，极易对参数方程的及的与参数方程等价的普通方程的混淆，认为是相等或者一致的，下面对其进行分析验证.

4.1 在x＝φ（t）（a≤t≤b）上应用拉格朗日中值定理

4.2 在y＝ψ（t）（a≤t≤b）上应用拉格朗日中值定理

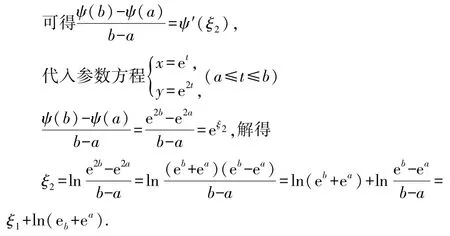
4.3 式中的ξ1与ξ2不一定相等

根据4.1与4.2的计算结果可知：≠.

4.4 在与参数方程等价的普通方程上应用柯西中值定理

4.5 结论

4.5.1 根据以上计算结果可知：≠≠，即参数方程及与参数方程等价的普通方程在（），（），（），（）相同的情况下，各自满足拉格朗日中值定理的不一定相等.

4.5.2 尽管≠≠，但柯西中值定理成立时的一定是来自（）、（）函数.此时当＝时，（），（）（≤≤）函数上应用拉格朗日中值定理不一定成立.

5 结束语

柯西中值定理和拉格朗日中值定理是一元微分学中最常用的两个工具，有很广泛的应用，如泰勒公式的证明、洛必达法则的证明、求极限等.中值定理是连接函数及其导数之间关系的桥梁，教材中要求掌握中值定理的证明也是研究生考试大纲范围，且有过真题.2009年硕士研究生考试数学一卷第18题（11分）就考查了拉格朗日中值定理证明：“证明拉格朗日中值定理：若函数（）在［，］上连续，在（，）可导，则存在∈（，），使得（）-（）＝（）（）.”本文通过对柯西中值定理的组成元素分析，及采用实例函数图形的直观表达，对柯西中值定理的证明有了另一个角度的理解，有利于学生更深入地掌握及灵活应用柯西中值定理.