基于“学材重构”的初中数学项目化课例设计——以“比一比，谁做的茶叶盒更大”为例

赵建平, 虞敬伟

(1.吴兴区教育局教学研究与培训中心，浙江 湖州 313000；2.吴兴区妙西学校，浙江 湖州 313000)

1 问题提出

初中九年级的学生已经有一定的空间观念、数感及符号感，加之八年级时已经历过“制作无盖长方体纸盒”的探究学习，九年级时进一步学习了立方体的表面展开图，感受了“从实际问题中抽象出数学问题—建立数学模型—综合应用已有的知识解决问题”的过程，项目开展时机相对成熟.浙江省湖州市吴兴区妙西镇是茶叶产销重镇，当地学生有真实的生活经历，在妙西学校开设一堂“比一比，谁做的茶叶盒更大”项目化学习的数学课具备一定的现实意义.

2 初步设想

本堂课秉承以解决学生身边的真实问题为项目任务，以项目活动中落实学生素养为主的原则，引导学生积极参与课堂，发挥学生的主观能动性.通过设计多个探究活动的方式让学生经历观察与猜测、实验与操作、抽象与交流、合作与展示、推理与反思等一系列数学活动，以学定教，体现学为中心的教学策略[1].同时，在教学中借助“几何画板”描绘图像，运用Excel辅助计算，让学生体会到信息技术是认识世界的有效手段和工具.思维导图如下：

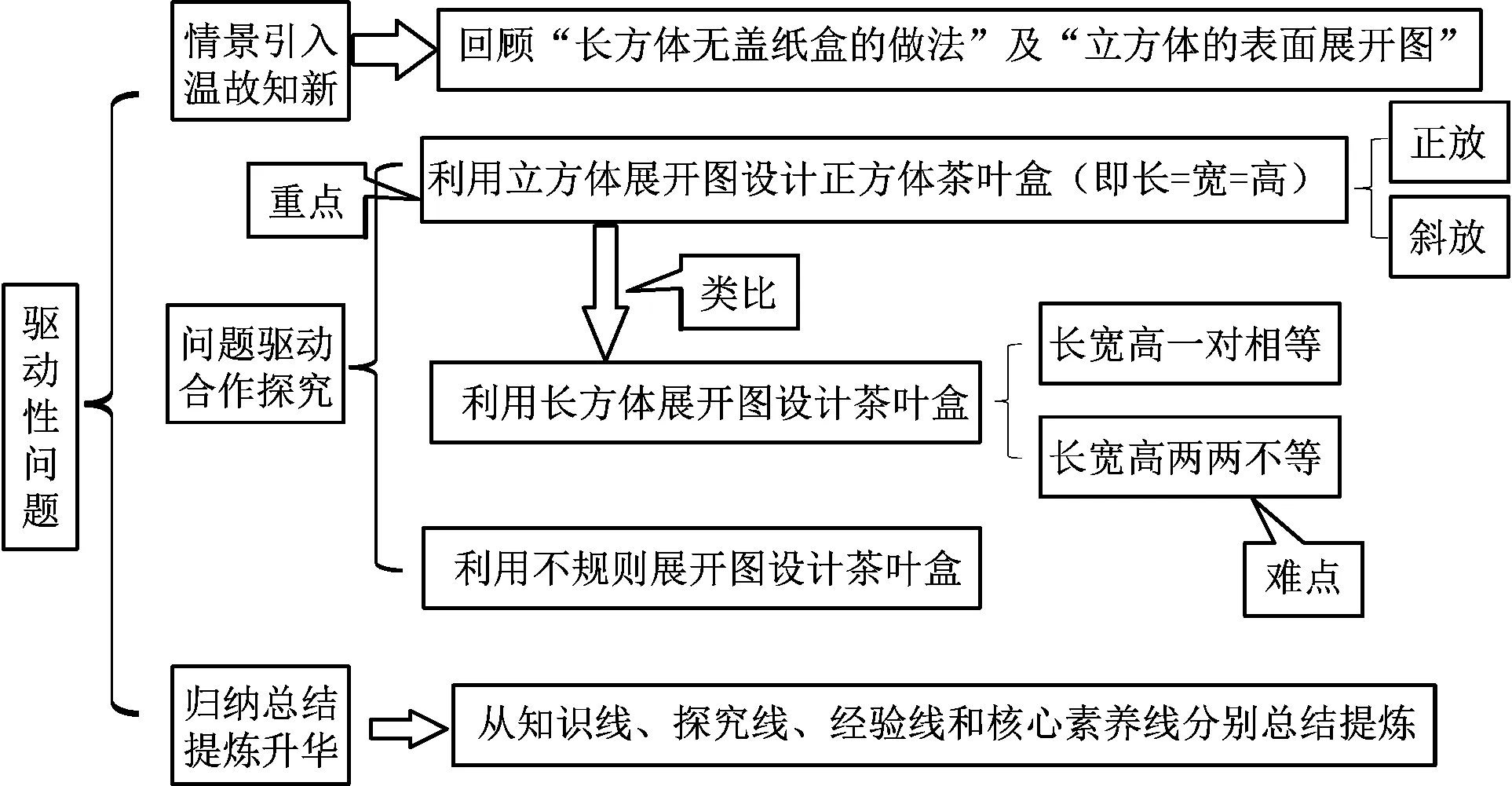
3 教学过程

3.1 情景引入，温故知新

妙西镇是茶叶产销重镇，是茶圣陆羽《茶经》撰写地.在当今节能减排的要求下，请将边长为20 cm的正方形纸片，经过适当裁剪，将剩余部分(必须是一张纸面)拼合成体积尽可能大的长方体(包括正方体)密闭茶叶盒(接缝不计).

问题1为了设计制作符合要求的茶叶盒，我们已经有哪些知识储备呢？

活动1师生一起回顾义务教育《数学》八年级下册探究学习了“无盖长方体纸盒”的制作和《数学》九年级下册学习的“立方体的表面展开图”.

设计意图通过PPT直观呈现，唤醒学生回忆相关的知识点，为下面的图形设计和计算论证做铺垫.

3.2 拆解项目，特例入手

请将一张边长为20 cm的正方形纸片，经过适当的裁剪，将剩余部分(必须是一张纸面)拼合成正方体密闭纸盒.

小组合作探究1在边长为20 cm的正方形纸片中正向设计立方体展开图(如图1).

图1

问题1请在边长为20 cm的正方形纸片中正向设计立方体展开图.

问题2比较你的设计方案和同学们的一样吗？孰优孰劣？

问题3小组合作，讨论影响体积大小的要素有哪些？

问题4通过本次活动，对你的方案改进有何启发？

设计意图分解项目，从特殊情况(正方体)展开学习，呈现言简意赅、指向明确的具体问题，起点较低,避免曲高和寡，利用磁力贴、正方形纸片、剪刀等工具，将学生置于有趣而富有挑战性的问题情境中.学生通过自己动手实践，在问题1和问题2的引导下观察、比较、归纳，通过问题3和问题4在操作中反思、提炼，积累数学基本活动经验，为后续进一步研究打好基础.

小组合作探究2在边长为20 cm的正方形纸片中斜向设计立方体展开图(如图2).

图2

设计意图经历探究1之后，学生已经具备了在正方形纸片内设计立方体展开图的经验，由此设置了探究2——在边长为20 cm的正方形纸片中斜向设计立方体展开图.此环节我们将选择有代表性的斜放方案进行展示，将重心由设计转到计算中来(正方形内接直角折线长度的求法)，同时感受图形的对称美.

3.3 类比探究，寻求一般

基于以上活动，若改成设计“长方体茶叶盒”，则体积会不会更大呢？我们将怎样开展研究呢？

小组合作探究3在边长为20 cm的正方形纸片中设计长方体展开图.

问题1小明同学思考：在相同条件下，把正方体茶叶盒改良成长方体茶叶盒，体积会不会更大？

他设计了如图3所示的方案：

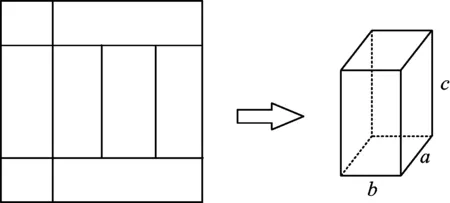
图3

问题2请尝试给展开图标注尺寸.

问题3请尝试用举例的方法，检验用小明的方案做的茶叶盒体积是否最大.

问题4我们分析得到了函数表达式V=b(10-b)(20-2b)是个“三次函数”，该如何探究它的最大值？请完成下列探究活动.

探究函数V=b(10-b)(20-2b)的最大值.

1)完成表1，判断当b在哪两个相邻整数之间时，V最大？

表1 b的值及对应的体积

2)观察表2，思考：我们是怎么提高精确度的？

表2 b的值及对应的体积

3)若要得到更精确的值，你将如何操作？

设计意图探究3学生将经历从特殊到一般的探究过程，类比正方体和长方体的区别和联系.从空间观念上从静态到动态的转变，需要更强的空间想象能力；从数与代数层面完成一元到二元、方程到函数的螺旋上升，具有一定梯度.通过问题1引导学生开展类比探究；以问题2为载体，帮助学生突破空间想象能力的瓶颈；问题3组织学生以举例的方式探求长方体茶叶盒体积的最大值，在此基础上驱动学生用函数观点刻画事物规律，“逼近法”呼之欲出；问题4学生将用“逼近法”探索函数的最大值，此环节要求较高，需要灵活运用函数解析法、列表法、图像法这3种表现形式，教师可以引导学生利用几何画板便捷地画出函数图像，用Excel快速地计算出相应的函数值.

3.3 回归特殊，创新思维

小组合作探究4探索有无体积更大的设计方案(如图4).

图4

设计意图回归特殊，进行正方体的不规则展开，发展学生的空间想象能力和创新思维能力，培养学生的发散思维能力与创造力.

4 教学反思

1)以串联教材多块知识解决问题为项目化学习框架，激发项目学习的“参与感”.

项目化学习的重要特征之一就是通过有意义的驱动性问题激发学生的兴趣，增加学生的学习热情，使其主动投入学习[2].本课着眼核心素养，结合地方特色，设计“比一比，谁做的茶叶盒更大”为驱动性问题，将学生置于现实的、有意义的、有挑战的实际问题中.教师着眼于“引”，引导学生发现问题、解决问题;学生着眼于“探”，自主合作探究知识、广泛交流，更加重视过程，学生获得正面的情感态度与价值观.本课把一元二次方程、正方体与长方体展开图、函数最值的探究串联在一起，一步步解决学生身边的真实问题，学生学习的积极性非常高.

2)以层次化驱动性任务为项目化学习的路径，注重知识建构的“可视化”.

本课学生需要经历从特殊到一般的研究过程，在活动中遵循“反复理解，螺旋上升”的规律[3].因此在学生完成特殊情况“正方体茶叶盒的设计”之后，引导学生进行复盘和反思，以思维导图为支架和辅助工具，提供学生交流反思的平台，让思维可视化，积累基本活动经验，为进一步研究指明方向.

3)以相关技术软件与直观教具为项目化学习的支持，提升问题解决的“可操作性”.

本课内容既有对已知知识的应用，也有对未知知识的探索，体现了层次性，开发了学生的探索潜能；同时驱动问题具有开放性，有利于点燃学生学习数学的兴趣和创新激情.基于问题本身的可操作性和探究性，在教学中教师多次利用教学工具做辅助，如利用“正方形纸片、磁力片、剪刀”等工具，组织学生进行操作探究，给学生创造“在‘做’中思考、在‘做’中发现、在‘做’中感悟”的平台；又如在探究“三次函数”最大值时，利用几何画板直观呈现函数图像，利用Excel计算工具替代机械运算，让学生真正投入到数学探究中去.

4)以知识与经验螺旋上升为项目化学习的感悟，落实核心素养的“渗透性”.

从知识角度看，本节课围绕“制作体积尽可能大的长方体茶叶盒”展开，将初中阶段长方体的表面展开图、特殊三角形、代数式(方程、函数)融为一体，强调知识的综合运用.课堂探究呈现从正方体到长方体、从“一元”到“二元”、从“低次”到“高次”的螺旋上升，最终以所学研究函数的经验探究“三次函数”的最大值.从基本活动经验的角度看，本堂课以活动为载体，以教学工具为辅助进行组织，从特殊情况到一般情况，结合手动、体动、脑动，促成结果的多样化和可对比性，在观察、猜测、实验、抽象、交流、合作、推理与反思等一系列活动中积累基本活动经验；从核心素养角度看，本堂课一开始从常规和已知的内容入手，通过反思和迁移，逐步发展到对未知知识的探索和对设计方案的创新中去，通过教师引导、学生探究所得，培养了学生数学抽象、逻辑推理和直观想象的数学核心素养，在结合图像分析的过程中，渗透数形结合思想[4].