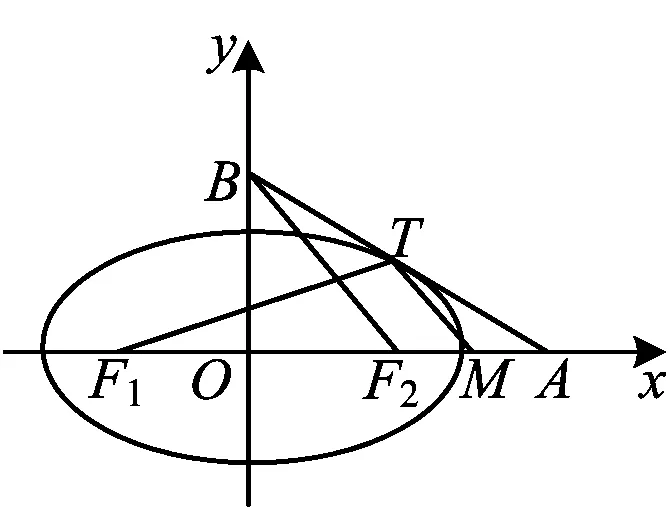
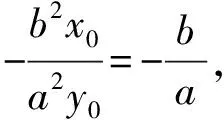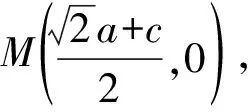关注生成教学 驱动深度学习

严丽香

(莆田市第四中学,福建 莆田 351100)

所谓深度学习，指的是学生在教师的引导下，围绕具有挑战性的学习内容，深度参与学习活动，从中体验与分享成功，从而获得发展的一种有意义的学习[1].由于学习的真正发生必须在个体已有知识经验的基础上生发出新的认知，即“生成知识”，因此基于深度学习的数学课堂教学，是在教师精心预设前提下的动态生成过程，是学生由未知走向成熟的过程.然而，在当前的高中数学课堂教学中，由于“生成教学”耗时长，不少教师常常选择回避，仍使用“灌输式”教学，直抛概念、结论，然后让学生进行大量的训练.“灌输式”教学表面上看似乎大大节约了课堂教学的时间，却忽视了学生思维成长中最重要的一个环节，为学生后续的学习留下了隐患，导致事倍功半.学生只有“生成”自己的理解，才能养成从数学的视角深层次地思考问题、解决问题的习惯，使体现数学本质、渗透数学思想、富有深度思维价值的课堂活动真正发生[2]，从而提升学生的关键能力，促进数学核心素养落地生根.

1 激活教材，在体验中生成

数学概念在其冰冷的形式化知识背后，隐含着生动活泼的、火热的数学思维.深度学习强调让学生亲历概念的发生、发展过程，使学生真切体验新知的来龙去脉.因此教师应精心设计教学活动，引导学生主动参与概念形成过程的观察分析、操作确认、抽象概括等一系列学习活动，把原本冰冷的静态的概念转化为学生火热的动态思考，促进学生的自主建构，提升数学抽象素养.

案例1人教A版高中《数学(必修2)》(新教材)“二面角”概念教学片段.

师：初中阶段我们学习了角的概念，它是如何定义的？

生1：从一点引出的两条射线所组成的图形称为角.

师：请类比角的概念来定义“二面角”.

生2:从一条直线出发的两个半平面组成的图形称做二面角.

师:很好！类比平面几何中角的记法∠AOB,我们应如何表示“二面角”？大家能举例说一说生活中存在的二面角模型吗？

生3：翻开的课本、打开的笔记本电脑等.

师:平时大家经常说“把门开大一点”,说明了二面角可以度量.我们应如何度量其大小呢？请回顾我们是如何刻画异面直线所成角、直线与平面所成角的？

生4：将“空间角”转化成“平面角”.

师：应该用什么样的“平面角”才能刻画二面角的大小呢？我们规定：如果两个半平面重合,那么二面角的大小是0°；如果两个半平面变成一个平面，那么二面角的大小是180°.请大家用卡片做个二面角,尝试画图找出刻画二面角大小的方法，并分组讨论.

(学生动手操作、讨论，教师选出小组代表进行多媒体展示，限于篇幅，图形略).

组1：过棱上任意一点分别在两个半平面内任作一条射线.

组2:我们在棱l上取一点O，在半平面α,β内分别作射线OA,OB，使它们与直线l所成的角均为60°.

组3：在棱l上取一点O，在半平面α,β内分别作射线OA,OB，使它们与直线l都垂直.

师:以上作法可以吗？

(大家思考、交流.)

生5:若按第一组的作法,则角的大小会随着所作的射线位置不同而大小不等，不满足“唯一性”.

生6:若按第二组作法,则所作的角也不唯一.当两个半平面重合时，出现平面角与0°矛盾的情形(如图1)；当两个半平面展开成一个平面时,出现平面角与180°矛盾的情形(如图2).

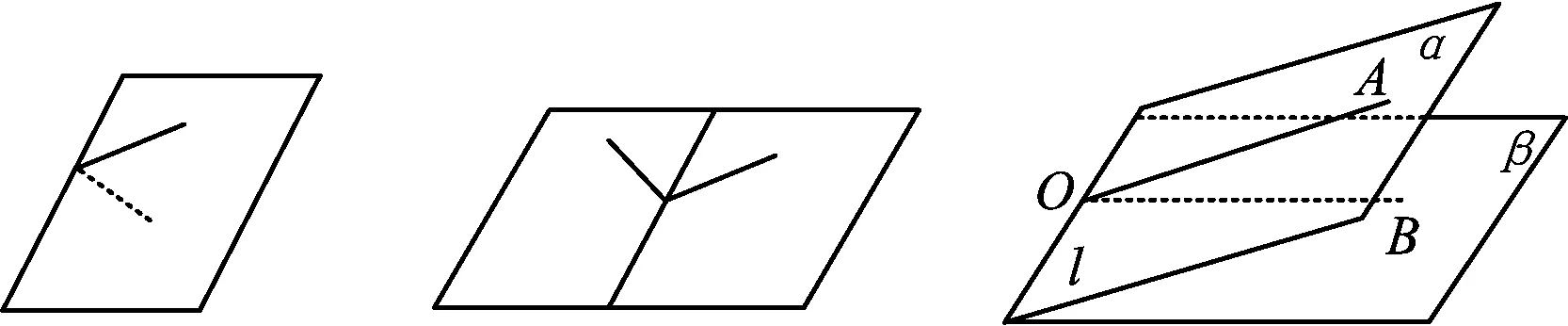
图1 图2 图3

生7:如图3，角的两边OA,OB都与棱l垂直,当二面角展开成平面时,射线OA,OB所成的角∠AOB为180°；当两个半平面重合时，平面角为0°.改变点O的位置时,由等角定理可知角的大小不变，具备唯一性，可以用来刻画“二面角”的大小.

师：分析得很到位！

教师利用多媒体展示二面角的平面角随二面角张开幅度变化的过程，让学生归纳概括“二面角的平面角”的定义.

如何度量二面角的大小是本节课的难点，突破难点的关键是引导学生根据已有的数学活动经验,用“平面化”的思想来刻画“二面角”.在案例1中，教师引导学生依据“直观感知—操作确认—抽象概括”的研究问题的一般方法，循序渐进地引导学生观察、操作、思维，并渗透类比、联想、化归等数学思想方法，启迪学生给出二面角的定义，并让学生亲身经历“二面角的平面角”的自然生成过程，使数学学习真正建立在学生自主探究的基础上，从而不断提升直观想象和数学抽象素养，达成深度学习.

2 善待偏差，在追问中生成

由于学生认知水平的局限，课堂生成难免存在一定的偏差.对于学生出现的错误，很多教师常常直接告知学生产生错误的原因与注意点.学生表面听懂了，但遇到类似情形，又会重复出现这种错误.究其原因，是这种“没有经过学生思考的直接告知”的方式，使他们对问题的认识处于浅层阶段，没有留下深刻的印象.因此教师应该把“告诉”改为“探究”，有针对性地引导学生在各种解法的分析比较中，暴露出可能存在的知识、能力等缺陷，并从差错中获得启迪，实现思维水平的进阶，从而让“错误”变得美丽，使课堂生成更具价值.

案例2已知二次函数f(x)=-x2+kx-1的图像与两端点分别为A(0,3),B(3,0)的线段有两个交点，求实数k的取值范围.

(教师用多媒体展示学生的一种典型错解，让学生思考.)

图4 图5 图6

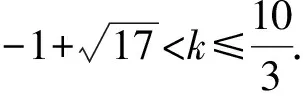
师：上面的解法对吗？

有的学生认为是对的，有的认为不对，但又说不出原因.教师没有直接指出错误，而是通过有针对性的点拨引导学生自己发现错因.学生们画图、思考，但不少学生仍没有找出错误原因.教师利用几何画板演示，学生终于发现以上方法以偏概全，忽视了图像的顶点在线段AB上或在AB下方的情况(如图5、图6).

师(追问)：本题是否可以换一个角度进行思考呢？

生1：本题可化归为方程-x2+kx-1=3-x,即x2-(k+1)x+4=0在区间[0,3]上有两个不相等的实数根.设x1,x2为方程的两个根，由于x1x2=4>0,只需0

生2：不对.如果取x1=2,x2=4,就能满足生1所说的条件，但x2=4>3.

师(追问)：很好!生2运用特殊值对答案的正确性进行了检验.那么，方程在[0,3]上有两个不相等的实数根的等价条件该如何用不等式进行表达呢？

生3：我认为应该等价于

即

师(追问):对！应该与0进行比较,才能找到等价条件,这是解题的关键.还有其他想法吗？

生4：可利用零点问题解决.设g(x)=x2-(k+1)x+4,问题转化为函数g(x)在区间[0，3]上有两个零点，由此得

师：生4将问题转化为g(x)在区间[0，3]上有两个零点，运用数形结合思想解决问题，很简洁.

师(追问)：是否可以对方程x2-(k+1)x+4=0进行变形，构造新的函数解决本题？

生6：当x≠0时，x2-(k+1)x+4=0,可化为

师：太棒了!生5和生6为大家提供了一种解决此类问题的简洁方法.若将方程x2-(k+1)x+4=0在[0,3]上有两个不等实数根变为不等式x2-(k+1)x+4>0在[0,3]上恒成立，求实数k的取值范围.你们能否类比以上方法求解吗？

引导学生从“合理性”的错误中学习，是促进课堂生成的一种艺术.一道“平凡”的习题，通过去伪存真、紧追不舍，启发学生探寻合理简便的解题途径，让学生从开始的迷茫到“懂得”，再到“精彩生成”，从而让学生对此类问题有了深度理解.实际上，学生认识上的偏差并不可怕，关键是教师要善于运用“合理性”的错误，引导学生展开辨析、讨论.通过合作交流引发学生识错、纠错，这样不仅深化了学生对问题本质的理解，而且完善了学生的认知结构，由“不识庐山真面目”向“会当凌绝顶，一览众山小”的境界升华，提升了数学核心素养[3].

3 反思感悟，在探究中生成

由于高中数学具有较强的抽象性、逻辑性等特点，许多学生的解题还仅仅停留在“模仿+练习”阶段，思维能力得不到应有的提高.因此解决问题之后，教师应留给学生体验与反思的时间，留给学生“顿悟”的机会，引领学生通过再思考、再认识，迸发出思维的灵性，深刻理解问题的内涵,促进课堂由“浅层生成”进入“深层生成”，使课堂教学取得事半功倍的效果[4].

1)求C的方程；

2)设C的左、右焦点分别为F1，F2，点M为线段AF2的中点，求证：∠ATM=∠AF1T.

为了提升问题的教育价值，当学生完成了本题之后,教师引导学生进行反思.

反思1第2)小题中∠ATM=∠AF1T是巧合，还是有规律可循？

学生思考并讨论，教师请学生代表发言.

师：生1很善于思考，我们一起来验证此猜想.

分析设T(x0,y0)，则切线l的方程为

可得

故

△TAM∽△F1AT，

即

∠ATM=∠AF1T.

反思2由上面的证明过程，有没有新的发现？

生2：我发现切点T是线段AB的中点，因此TM∥BF2，从而∠ATM=∠ABF2(如图7).又∠ATM=∠AF1T，由此我猜想点F1,F2,T,B共圆.

图7

师：生2思维敏锐，大家来验证一下他的结论是否成立.

学生经过证明，得到如下结论：

教师继续引领学生反思：

反思3椭圆有以上性质,双曲线是否有相似的结论呢？

课堂气氛非常活跃，学生们跃跃欲试,经过探究，得到如下结论：

图8

师：太好了！类比椭圆与双曲线之间的相似性质发现规律，这是数学发现的重要策略.

这种自省形式的反思一旦成为解题之后的自觉行动，就能促使学生以高远的观点、宽广的视野、理性的眼光去思考问题、解决问题，从思维、结构等方面寻求“生长点”，从而使数学课堂不断出新、出彩，在深度学习中让有限的数学课堂“生长”出无限的能力.