深度探究育思维 追根溯源促素养
——以一道期末试题的解法与背景探究为例
廖爱国
(云和中学,浙江 云和 323600)
数学思维能力,是指人们能够用数学的观点去提出问题、分析问题和解决问题的能力,它是学生数学学习的关键.教师通过研究新教材、设计教学方法、精选课后作业及研究试题命制,从而落实学生数学思维能力的培育,促进学生六大数学核心素养的提升.在新一轮高考改革中,面对新教材(2019年人教A版普通高中《数学》),高中数学教师面临着巨大的挑战,新教材的编写处处渗透着新课标的育人理念,值得每位教师在教学中细细体会,真正地把教材用好,避免在教学中“穿新鞋,走老路”.再则,浙江省将在2023年的高考中使用全国卷,认真研究数学高考全国卷,把握好高考命题方向至关重要!
下面笔者通过对一道浙江省丽水市高二数学期末试题的探究,分享自己对提升学生数学思维能力的一些想法.
1 探析解法,双重视角培育思维
1.1 试题呈现
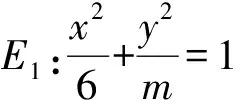
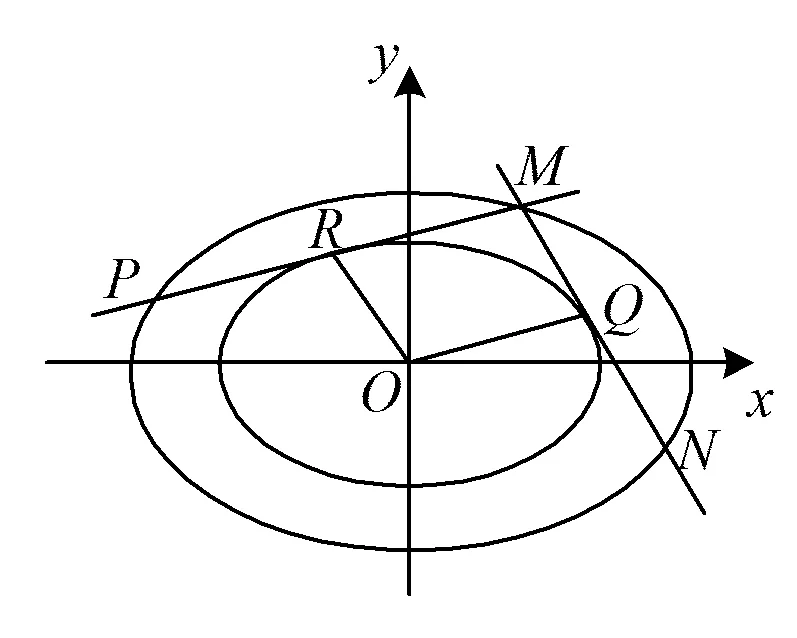
图1
1)求实数m的值;
2)求证:点Q是线段MN的中点;
3)求四边形OQMR面积的最大值.
笔者有幸参加了丽水市2021学年高二数学期末试题的命制工作.本题为试卷的最后一道解答题,是解析几何中有关直线与椭圆位置关系的综合题,考查了学生转化、逻辑推理、运算求解能力.试题背景丰富,起点低,坡度缓,解法多样,能很好地区分出学生不同的数学思维水平.本题全市去零平均分为3.78分,难度系数为0.27,学生答题情况不尽如人意,充分反映了学生在知识学习中的漏洞.
1.2 解法探究
视角1韦达定理结合面积公式.
易知m=3,下面分析第2)和第3)小题.
2)证法1若直线MN的斜率不存在,则由椭圆的对称性可知点Q必为线段MN的中点.若直线MN的斜率存在(设斜率为k),则直线MN的方程为y=kx+b,点M(x1,y1),N(x2,y2),Q(x0,y0).
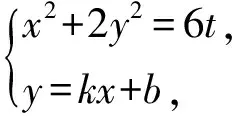
(1+2k2)x2+4kbx+2b2-6t=0.
(1)
因为直线MN与椭圆E2相切,所以由韦达定理得
由Δ=0,得
3t(2k2+1)=b2.
在式(1)中,令t=1,得
从而
即点Q是线段MN的中点.
3)解法1若直线MN的斜率不存在,则直线MN的方程为
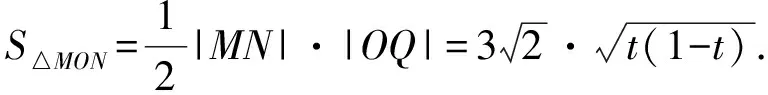
若直线MN的斜率存在(设斜率为k),则
结合3t(2k2+1)=b2,得
由上可知△MON的面积与直线MN的斜率无关,因此S△MOP=S△MON.而Q,R分别为MN,MP的中点,故
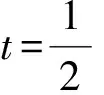
视角2椭圆仿射变换.
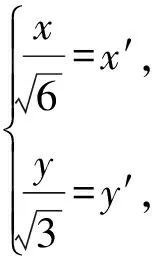
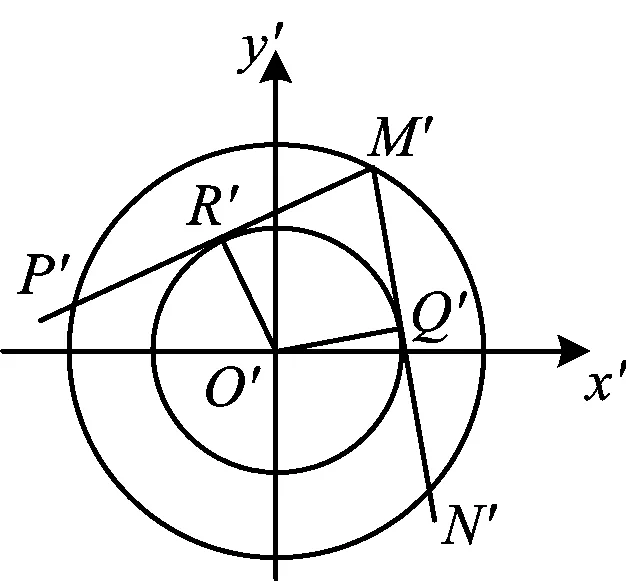
图2
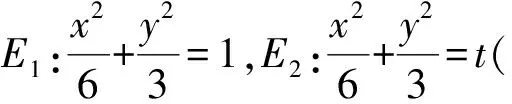
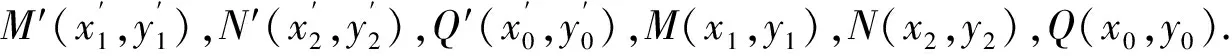
从而
即点Q是线段MN的中点.
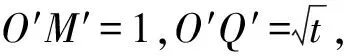
从而
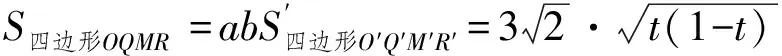
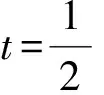
评注本题涉及直线与椭圆相交、相切及四边形面积问题.视角1按照“设、联、消、韦、面积公式”的常规思路求解,充分体现了解析几何用坐标法解决几何问题的核心思想,求解思路清晰,但有一定的运算量,对四边形面积的合理转化也是本题的难点.视角2借助椭圆仿射变换,化“椭”为“圆”,利用圆的性质求解,降低了计算难度,但是对椭圆仿射变换的性质还是需要先证后用,两个视角给不同数学思维水平的学生都有发挥的空间.
2 试题还原,命题点滴提升能力
2.1 试题初稿
著名数学家华罗庚曾说:“命题比解题难,命题要测得出水平,测得出能力.”[1]因此,题目需如玉石般经历千雕万琢方能成就好题,本道期末试题的命制也是几经修改、精心打磨的.下面选取命题时的其中一稿与读者分享.
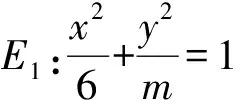
1)求实数m的值.
2)求△OMN面积的最大值.
3)如图3,椭圆E2的两条互相垂直的动切线l1,l2交于点P.记点P的轨迹为C,曲线C的切线l3与椭圆E1总有两个不同的交点A,B,切点为T,若|TA|·|TB|为定值,求椭圆E2的方程.
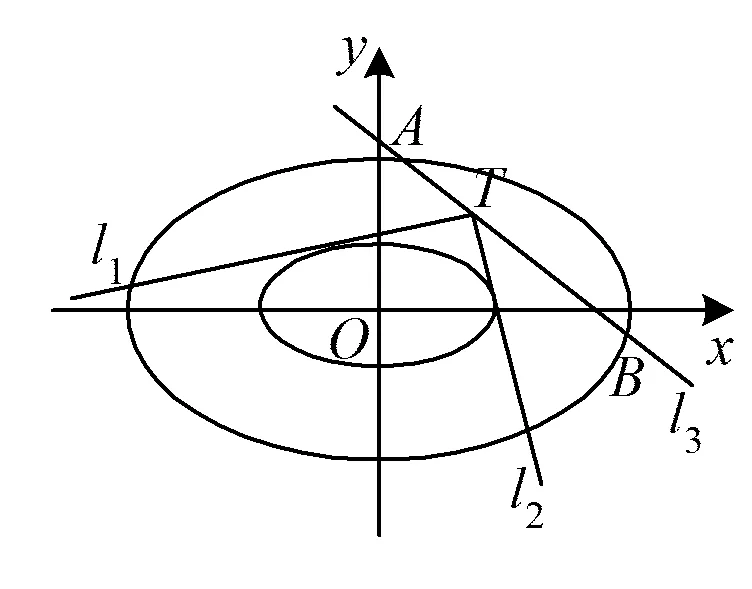
图3
2.2 解法探究
下面仅分析第3)小题.
解法1当切线l1,l2的斜率都存在时,设过点P(x0,y0)的椭圆E2的切线方程为
y-y0=k(x-x0).
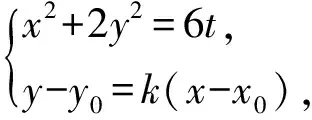
(1+2k2)x2+4k(y-kx0)x+2(y0-kx0)2-6t=0,
由Δ=0,得
因此,动切线l1,l2的斜率k1,k2是此方程的两个根,故
即
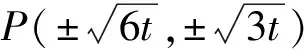
故点P的轨迹C的方程为
x2+y2=9t(其中0 ①当切线l3的斜率不存在时, ②当切线l3的斜率为0时, |TA|·|TB|=6-18t. 下面只需证明当切线l3的斜率存在且不为0时,恒有|TA|·|TB|=2成立. ③当切线l3的斜率存在且不为0时,设切线l3:y=kx+b,点T(x0,y0),A(x1,y1),B(x2,y2),由相切得 即 b2=2(1+k2). (1+2k2)x2+4kbx+2b2-6=0, 从而 |TA|·|TB|=(1+k2)|x0-x1|·|x0-x2| |TA|·|TB|=2=|TO|2. 为此,要证明情形③中的|TA|·|TB|=2恒成立有以下解法: =(1+k2)x1x2+kb(x1+x2)+b2 得 |TA|·|TB|=|TO|2=2. 下同解法1. 评注本题是一道直线与椭圆、圆位置关系的综合问题,考查了学生的数学运算与逻辑推理素养,涉及解析几何的分类讨论、同构式等思想.3个小题层层递进,能较好地考查学生的数学思维能力.命题时,总体感觉本题计算量过大,涉及结论性的内容较多,试题结构不够漂亮,为此在后面修改时,既降低了题目的难度,又力求表述更加简洁. 罗增儒教授说过:“数学学习中真正发生数学的地方都无一例外地充满着数学解题活动.”至此,虽然我们已经完成了对例1与例2的解法探究,但是解题活动仍然在继续.对试题背景溯源,真正明白命题者的出题背景与命制意图,才能进一步拓宽我们的视野,高观点下思考问题,进而指导我们更好地为教学服务! 试题命制的背景之一为蒙日圆,例2第3)小题中点的轨迹即为蒙日圆,它交汇了椭圆、切线、圆等重点内容,是命题者的重要素材.蒙日圆又能延伸出许多重要的性质和结论. 相似椭圆是例1与例2的另一重要背景,例1中第2)和第3)小题正是相似椭圆的两个重要性质.而相似椭圆在2015年山东省数学高考理科卷中也出现过,与相似三角形类似,若两个椭圆的长轴与短轴对应成比例,则称两个椭圆相似[2].根据定义可以得到相似椭圆有如下优美性质: 2)过椭圆C1上一点P引椭圆C2的两条切线PA,PB,分别交C1于点A,B,切点分别为M,N,则直线OP平分椭圆C2的弦MN; 以上定理1与性质1的证明不再赘述,留给读者思考. 数学是思维的学科,在《普通高中数学课程标准(2017年版2020年修订)》中明确提出:要发展学生的数学思维能力.而学生的数学思维能力并不是一朝一夕养成的,它需要数学教师在日常教学中慢慢渗透、耐心培养,通过对学生数学思维能力的培育,促进学生数学核心素养的提升.经历了前面的试题命制与探究的整个过程,笔者有以下几点启示: 1)重视三基,落实通法,夯实学生数学思维的基础性. 学生扎实掌握数学的基础知识、基本技能,领悟数学的基本思想方法是解决数学问题的核心.纵观整个探究过程,虽然问题解决不乏好的方法,但是其最根本的方法始终围绕着解析几何的本质,即用代数方法研究几何问题[3].在教学中,我们应更加重视学生对基本概念的理解和基本方法的训练,抓常规、重落实,打好培养学生数学思维的基础性. 2)勤于探究,拓宽视野,助力学生数学思维的发散性. “教而不研则浅,研而不教则空”.作为学生数学学习的引路人,教师只有不断地学习与积累,才能成就自身更扎实的专业素养,特别是对一些好的试题,它是一个命题者甚至是整个命题团队的智慧结晶,更加值得我们学习.通过试题研究,挖掘试题的本质,看透其数学背景,我们才能在高观点的指引下,助力学生培育数学发散思维,落实数学核心素养. 3)激发兴趣,培养意志,培育学生数学思维的坚韧性. 一题一世界,数学中的难题往往都是一个个小题组成的,由浅入深,因此学生在解题时,要树立解题信心,遇到思维与运算困难,要有坚定的意志力.教师在教学中不仅需要传授知识与技巧,更要多采用启发式教学,激发学生的学习兴趣,并注重对学生数学思维品质的培养.
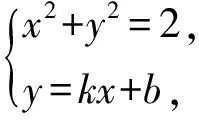
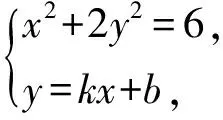
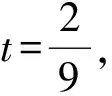
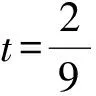
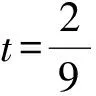
3 背景溯源,高观点下促进素养
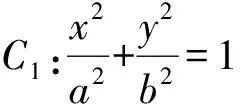
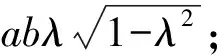
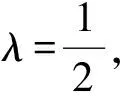
4 基于学生数学思维能力培育的探究启示

