FRP筋异强混凝土叠浇梁挠度与延性研究

张建波,陈升平,卢应发

(湖北工业大学土木建筑与环境学院，武汉 430068)

0 引 言

纤维增强聚合物(fiber reinforced polymer， FRP)筋混凝土结构多用于易腐蚀的环境中，以解决因钢筋锈蚀而引起的安全性和经济性问题[1]。而与钢筋混凝土梁相比，FRP筋混凝土梁具有较大的变形和脆性等问题，同样限制了其在工程中的应用与推广。为解决FRP筋混凝土梁变形较大以及延性较低的问题，研究人员在FRP筋混凝土梁中掺入钢纤维，利用钢纤维的增韧作用来提高梁的整体性能。研究[2]结果表明，钢纤维的掺入可以有效抑制FRP筋混凝土梁的变形。

然而，当FRP筋钢纤维混凝土梁开裂后，裂缝间的钢纤维更易受到锈蚀，同样会引起结构的耐久性不足等问题[3]。由于钢纤维的掺入可以提高混凝土极限状态下的压缩应变[4]，构件的破坏从脆性向韧性发展。因此，为发挥出FRP筋、钢纤维对构件的增韧和延性作用，梁受压区域采用钢纤维混凝土,受拉区采用素混凝土制作成FRP筋异强混凝土叠浇梁，利用提高受压区的极限压缩应变来提升FRP筋混凝土梁的延性。该类型梁将钢纤维的增强、增韧作用与素混凝土的经济性结合起来，具有良好的经济效益。

挠度与延性是FRP筋混凝土梁的重要设计指标，要求结构在满足承载力的同时，还需要有一定的延性。延性结构有利于吸收和消耗动荷载作用下的能量，在破坏前具有明显的预兆，有效减轻结构的损伤。程晟钊[5]通过16根玄武岩纤维增强聚合物(basalt fiber reinforced polymer, BFRP)筋钢纤维混凝土梁的受弯试验，测得BFRP筋钢纤维混凝土梁的延性系数均大于4，表明钢纤维的掺入有效改善了BFRP筋混凝土梁的脆性问题。陈升平等[6]以钢纤维体积率为变量，通过6根FRP筋梁的四点弯曲试验，研究了钢纤维对FRP筋混凝土梁延性的影响，结果表明，钢纤维可以显著提升FRP筋混凝土梁的延性。目前，对于FRP筋混凝土梁的研究都集中于单一强度，而从FRP筋混凝土梁的受弯破坏模式中可以看出，受拉区域的混凝土强度并没有得到充分发挥[7]。Iskhakov等[8]、周威等[9]通过对异强混凝土梁的弯曲试验，验证了异强混凝土叠浇梁的可行性。本文结合已有的研究成果，探讨了FRP筋异强混凝土叠浇梁的弯曲性能，并提出了适用于FRP筋异强混凝土叠浇梁的挠度计算公式和延性评价方法。

1 实 验

1.1 试验梁设计

由于FRP筋具有较大的脆性，对FRP筋混凝土梁的设计规范一般将该类梁设计为超筋破坏。设计6根尺寸为150 mm×300 mm×2100 mm的超筋试验梁，第一组以钢纤维混凝土叠浇层厚度180 mm为定量，叠浇层钢纤维的掺量(体积分数)依次为0.5%(F2)、1.0%(F3)、1.5%(F4)。第二组以钢纤维1.0%的掺量为定量，钢纤维混凝土叠浇层厚度依次为180 mm(F3)、210 mm(F5)、300 mm(F6)。对照组为1根FRP筋混凝土梁(F1)。试验梁尺寸如图1所示，试验梁参数如表1所示。

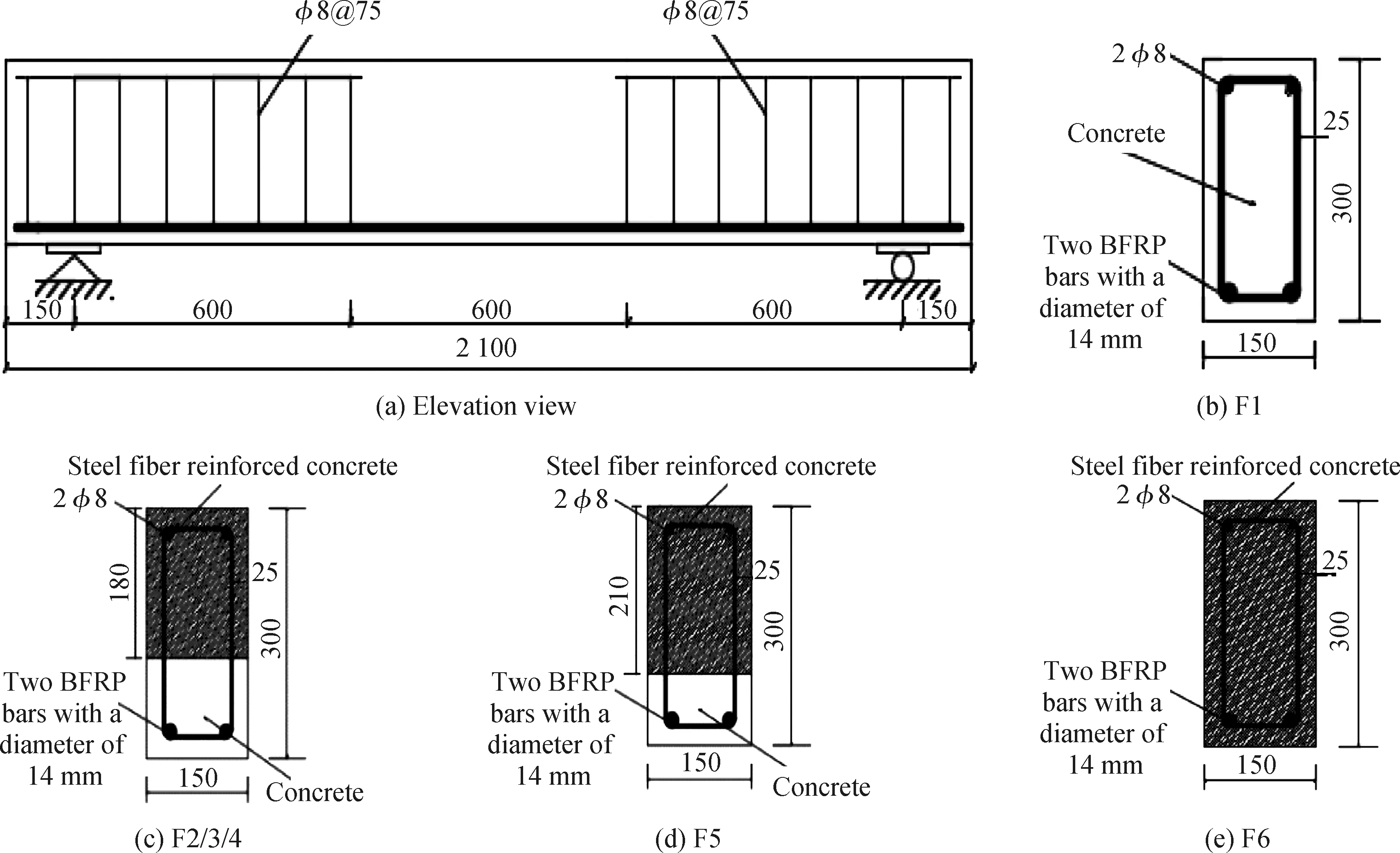
图1 试验梁尺寸示意图(单位：mm)Fig.1 Schematic of test beam size (unit: mm)

表1 试验梁参数Table 1 Parameters of test beam

1.2 试验梁原料

试验梁所用原料如下：细骨料采用河砂，适量聚羧酸高性能减水剂，铣削波浪型钢纤维，水泥采用P·O 42.5级普通硅酸盐水泥，一级粉煤灰，石子采用碎石，受力筋为BFRP筋，实验室用水，架立筋与箍筋采用三级螺纹钢筋。试验梁混凝土配合比如表2所示，筋材力学性能如表3所示，钢纤维力学性能如表4所示。

表2 试验梁配合比Table 2 Test beam mix ratio /(kg·m-3)

表3 筋材力学性能Table 3 Mechanical properties of reinforcement material

表4 钢纤维力学性能Table 4 Mechanical properties of steel fiber

1.3 主要测试内容

本次试验采用电液伺服微机压力控制实验机对试件梁进行三分点弯曲试验，加载设备如图2所示。应变与荷载采集采用DH3816N静态应变测试系统，裂缝的记录采用裂缝测宽仪、尺子。记录内容包括：开裂与限荷载、应变数据、跨中位移与裂缝宽度等。进行预加载时，观察各项设备读数是否正常。

图2 加载设备Fig.2 Loading device

2 结果与讨论

2.1 破坏模式

FRP筋混凝土梁(F1)的破坏如图3所示。在达到承载力极限后，FRP筋混凝土梁受压区混凝土突然崩裂，破坏时无明显征兆，具有明显的脆性。而FRP筋异强混凝土叠浇梁在达到承载力极限后，试验梁上部钢纤维混凝土缓慢隆起，随着荷载的施加，隆起的钢纤维混凝土不断升高直到试验梁受压破坏，相较于试验梁F1具有明显的延性，FRP筋异强混凝土叠浇梁的破坏如图4所示。且相较于试验梁F1，钢纤维的掺加使FRP筋异强混凝土叠浇梁的极限承载力提升了9%～33%。

图3 FRP筋混凝土梁Fig.3 Concrete beam with FRP bars

图4 FRP筋异强混凝土叠浇梁Fig.4 FRP bars reinforced concrete superposed beams

2.2 钢纤维对跨中挠度的影响

钢纤维掺量对跨中挠度的影响如图5所示。在加载初期，跨中挠度与荷载呈线性增加，当裂缝出现后梁的整体刚度降低，跨中挠度随荷载的施加呈曲线增长。随着钢纤维掺量的增加，相较于FRP筋混凝土梁，FRP筋异强混凝土叠浇梁在正常使用状态下跨中位移减少了4%～21%,这是由于钢纤维的掺入增强了试验梁的局部抗压强度，从而增强了试验梁的抗弯性能。

图5 钢纤维掺量对挠度的影响Fig.5 Effect of steel fiber content on deflection

钢纤维叠浇层厚度对跨中挠度的影响如图6所示。随着叠浇层厚度的增加，FRP筋异强混凝土叠浇梁在正常使用状态下跨中位移减少了14%～18%，这是由于钢纤维的分布高度增强了梁的整体刚度。

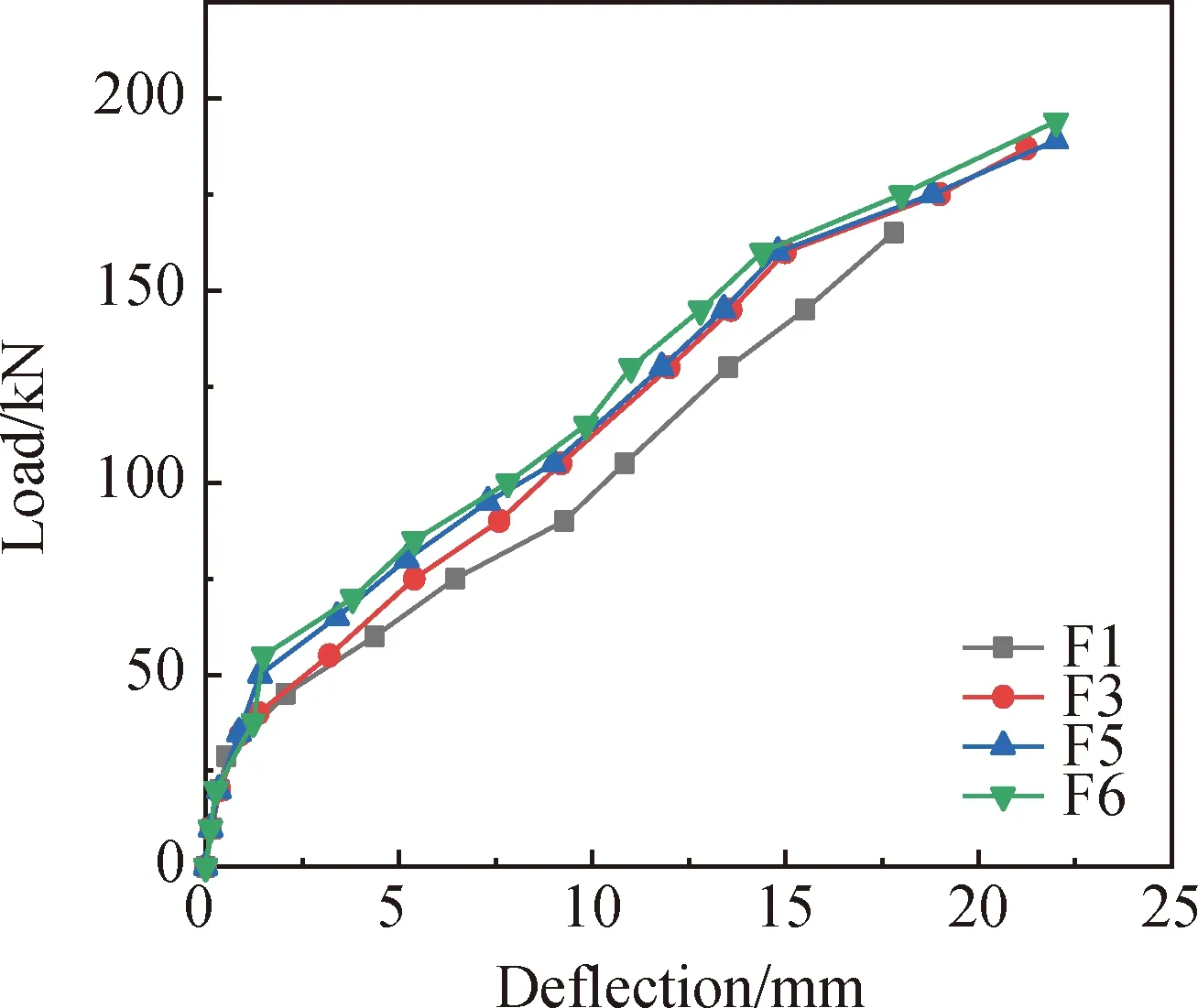
图6 钢纤维混凝土叠浇层厚度对挠度的影响Fig.6 Effect of thickness of steel fiber reinforced concretesuperposed layer on deflection

2.3 钢纤维对裂缝宽度的影响

钢纤维掺量对最大裂缝宽度的影响如图7所示。FRP筋异强混凝土叠浇梁在正常使用状态下裂缝宽度的发展与试验梁F1相似，这是由于正常使用状态下构件的抗裂作用主要由受力纵筋承担，而FRP筋异强混凝土叠浇梁的下部受拉区并未掺入钢纤维，此时钢纤维的作用并不明显。当施加荷载超过正常使用极限状态后，随着钢纤维掺量的增加，钢纤维对裂缝宽度的抑制越明显，这是由于裂缝间钢纤维传递应力。相较于试验梁F1，在极限荷载状态下FRP筋异强混凝土叠浇梁最大裂缝宽度减少了19%～28%。

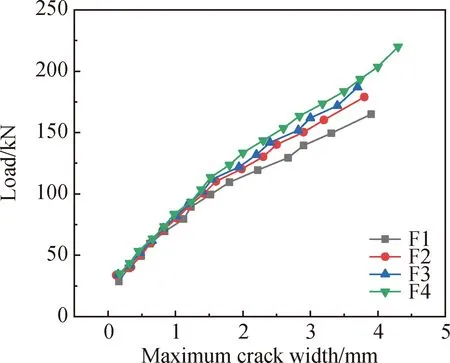
图7 钢纤维掺量对最大裂缝宽度的影响Fig.7 Effect of steel fiber content on maximum crack width

钢纤维叠浇层厚度对最大裂缝宽度的影响如图8所示。在钢纤维掺量相同的情况下，钢纤维叠浇层厚度越大，对最大裂缝宽度的限制越明显。在极限荷载状态下FRP筋异强混凝土叠浇梁最大裂缝宽度减少22%～38%。

图8 钢纤维混凝土叠浇层厚度对最大裂缝宽度的影响Fig.8 Effect of thickness of steel fiber reinforced concretesuperposed layer on maximum crack width

3 挠度计算与延性评价

3.1 挠度计算

我国对于FRP筋混凝土挠度的计算沿用了钢筋混凝土梁的计算方法：

f=Pa48EcIe(3l2-4a2)

(1)

式中：f为三分点加载方式下受弯构件的跨中位，mm；P为荷载，kN；l为试验梁跨度，mm；a为支座到加载点的距离，mm；Ec为混凝土的弹性模量，MPa;Ie为有效惯性矩，mm。

由于FRP筋变形较大的特点，以及钢纤维的加入改变混凝土梁的截面刚度，因此有必要对FRP筋异强混凝土叠浇梁的挠度计算公式进行修正。

文献[10]在考虑了FRP筋的弹性模量和粘结性能等因素下，建立了梁的截面有效惯性矩的计算公式：

Ie=Icr+(βIg-Icr)(McrM)3

(2)

式中：Ie为截面有效惯性矩，mm4；β为类型系数；Icr为开裂截面惯性矩，mm4；Ig为初始截面惯性矩,mm4；Mcr为开裂弯矩,kN·mm；M为使用弯矩，kN·mm。

(1)修正BFRP筋类型系数

由于钢纤维的掺加，对于FRP筋异强混凝土叠浇梁引入钢纤维特征值λsf，则对于BFRP筋β1的计算公式如下：

β1=α(EfEs+1)(1+υλsf)

(3)

λsf=lfdfvf

(4)

式中：β1为调整后的系数；Ef、Es为相同直径的BFRP筋、钢筋的弹性模量，MPa；α为粘结影响系数，取值0.5；υ为折减系数，建议取值0.2;lf为钢纤维长度；df为钢纤维的等效直径；vf为钢纤维体积率。

(2)修正FRP筋异强混凝土叠浇梁的初始截面惯性

采用材料力学的计算方法换算截面惯性矩如图9所示。将FRP筋异强混凝土叠浇梁进行截面换算：

x0=αEfcbd22+b(h-d)(h+d2)+nAfh0(αEf-1)αEfcbd+b(h-d)+nAf(αEf-1)

(5)

I′g=αEfcb(d-x0)33+αEfcbx303+b(h-d)(h+d2-x0)2+b(h-d)312+nAf(h0-x0)2(αEf-1)

(6)

式中：I′g为FRP筋异强混凝土叠浇梁初始截面惯性矩,mm4；αEfc为钢纤维混凝土与混凝土的弹性模量之比；αEf为BFRP筋与混凝土弹性模量之比；b为梁宽,mm；d为钢纤维混凝土叠浇层厚度,mm；h0为截面有效高度,mm；x0为修正后的截面形心到梁上表面的距离,mm；n为纵筋根数;Af为FRP筋的截面面积。

(3)修正FRP筋异强混凝土叠浇梁开裂截面惯性矩

由于钢纤维掺加在试验梁的受压区域，因此将受压区的钢纤维等效为钢筋。等效简化原则如下：

1)钢纤维混凝土的高度与梁受压区高度相同；

2)不考虑受拉区钢纤维的作用；

3)钢纤维在受压区域内分布均匀。

钢纤维等效为微钢筋如图10所示。钢纤维数量采用增强有效系数代替[11]：

nfasf=ηsfbxcrvf

(7)

式中：nf为钢纤维根数；asf为单根钢纤维截面面积，mm2；ηsf为钢纤维的有效系数，根据文献[12]取0.16；xcr为受压区高度，mm。

由拉压区对中和轴的矩等值得到：

b-bsf2x2cr+αEfcasfnxcr2=nAf(h0-xcr)

(8)

钢纤维等效宽度：

bsf=nfαEfcasfxcr=αEfcηsfbvf

(9)

式中：bsf为等效后的微钢筋宽度,mm。

xcr=-(αEfcasfnf2+nAf)+(αEfcasfnf2+nAf)2+2(b-bsf)nAfh0b-bsf

(10)

I′cr=(b-bsf)x3cr3+nAf(h0-xcr)2+bsfx3cr12+aEfcnfasf(xcr2)2

(11)

式中：I′cr为FRP筋异强混凝土梁的开裂截面惯性矩。

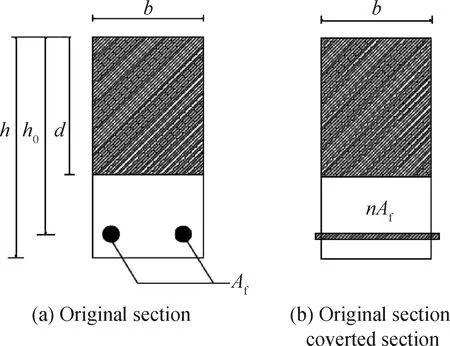
图9 截面换算Fig.9 Cross section conversion

图10 等效截面Fig.10 Equivalent section

3.2 延性评价方法

(1)传统延性指标法

传统钢筋混凝土的位移延性因子：

μD=DuDy

(12)

式中：μD为位移延性因子；Du为极限变形；Dy为初始屈服时的变形。

(2)延性的综合性能指标

由于FRP筋具有较高的抗拉强度，祁皑等[13]将FRP筋混凝土梁的荷载-挠度曲线理想化为一条直线，提出FRP筋混凝土梁延性的综合指标：

S=MUM0.001

(13)

D=φUφ0.001

(14)

J=SD=[φUφ0.001][MUM0.001]

(15)

式中：MU为极限弯矩，kN·mm;φU为极限弯矩所对应的曲率，mm-1；M0.001、φ0.001分别为混凝土受压边缘应变为εc=0.001时对应的弯矩(kN·mm)与曲率(mm-1)。

(3)FRP筋异强混凝土叠浇梁延性评价方法

在ACI440.1R-15[14]规范中对于FRP筋混凝土梁的设计由其满足适用性的变形控制，因此对于FRP筋混凝土梁延性的评价为极限状态所消耗的能量与正常使用极限状态(跨中位移为l/200时)下所消耗的能量之比，此评价方法具有较好的适用性。因此，对于FRP筋异强混凝土叠浇梁的延性可评价为：

μ=EuEscr

(16)

式中：Eu为极限状态下消耗的能量，kN·mm；Escr为正常使用极限状态下消耗的能量，kN·mm。

4 试验结果验证

由于FRP筋梁的变形较大，其设计通常由满足适用性的变形要求控制，因此在使用状态下，将试验值、跨中挠度计算值和规范GB 50608—2010[15]计算值进行对比，计算结果对比如图11所示，计算值与试验值吻合较好。

图11 挠度对比曲线Fig.11 Comparison curves of deflection

FRP筋异强混凝土叠浇梁的延性计算结果如表5所示。从表中可以看出，相较于试验梁F1，试验梁F2、F3、F4的延性提高了22%、35%、89%，试验梁F5、F6的延性提高了34%、34%。

表5 延性计算结果Table 5 Ductility calculation results

5 结 论

(1)FRP筋异强混凝土梁在受弯过程中的整体性较好，叠浇界面在受弯过程中未出现剪切滑移现象，且其破坏形态均符合超筋延性破坏的特征。

(2)FRP筋异强混凝土叠浇梁与FRP筋全截面钢纤维混凝土梁在极限状态下的破坏形态相近，与FRP筋混凝土梁相比表现出明显的韧性。

(3)受压区钢纤维的掺量对试验梁延性的影响较为显著，而钢纤维混凝土叠浇层厚度对试验梁延性的影响较小。

(4)FRP筋异强混凝土叠浇梁在正常使用状态下最大裂缝的发展与FRP筋混凝土梁较为相近，但在极限承载力状态下能够有效抑制裂缝的发展。

(5)建立了适用于FRP筋异强混凝土叠浇梁挠度计算公式和延性评价方法，为FRP筋异强混凝土叠浇梁在实际工程中的应用与推广提供理论依据。