基于强震动数据的等强度延性谱影响因素分析

来庆辉　胡进军　刘璇　谢礼立

要：基于5 500余条峰值加速度大于50 gal的水平向地震动数据，采用双线性模型计算了单自由度体系弹塑性反应，从地震信息参数和地震动参数2方面分析了影响等强度延性谱的因素。首先在场地分类的基础上按震中距和震级大小将地震动分组，分析了震中距远近和震级大小对等强度延性谱的影响;然后在地震动参数方面分析了反映幅值、频谱以及持时的峰值速度（PGV）、有效峰值加速度（EPA）以及Bolt持时等代表参数，并且根据PGV，EPA和Bolt持时的大小分组，分析了其对等强度延性谱的影响，结果表明：①在大部分周期內，各组等强度延性谱值差异较大，在各个场地内震中距和震级较大时，对应的延性谱值较大;②分组效果最好的地震动参数为PGV，其次是Bolt持时，当根据EPA分组时，分组结果最不理想。

关键词：地震动参数;非弹性反应;等强度延性谱;影响因素

中图分类号：P315.91 文献标志码：A 文章编号：1000-0666（2019）04-0594-07

0 引言

弹塑性时程分析方法经常被用于预测结构地震响应和抗震性能评估。Newmark和Hall（1973）最早提出了“等能量原理”和“等位移原理”来研究屈服强度系数和延性系数的关系。近年来更多的专家和学者倾向于研究弹塑性反应谱（何海健等，2018;薛尚铃等，2017），翟长海等（2006），Xie和Zhai（2003）利用实际地震动记录研究了恢复力模型、阻尼比等结构参数对等延性地震抗力谱的影响;易伟建和张海燕（2005）对等延性强度需求谱和等强度延性需求谱的优缺点进行了对比和分析;Miranda（1993）对100多条地震动记录研究发现，结构的弹塑性反应谱与场地因素有关;周定松（2004）研究认为场地分类和设计分组对等强度延性谱有显著影响;翟长海等（2008）和Zhai等（2007）根据峰值速度、峰值加速度与速度的比值以及最大增量速度等地震动参数对近断层脉冲型地震动进行分组，研究近断层脉冲型地震动非线性位移谱比的变化情况，得出不同地震动参数对不同周期内位移谱比的影响。因此越来越多的研究人员将重心从研究等延性强度反应谱转移到研究等强度延性反应谱上。

本文结合相关研究成果和文献，使用Newmark方法计算非线性体系的动力反应。通过动力非弹性反应来分析等强度延性谱在地震信息参数和地震动参数影响下的变化规律，并对这种规律进行分析。

1 调幅因子对等强度延性谱的影响

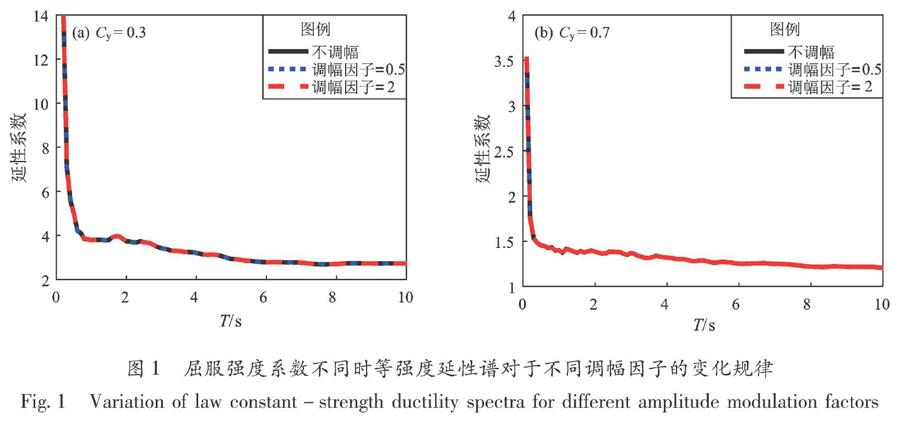
在抗震设计中，最常用的挑选地震动的方法就是将地震动记录调幅使其与设计谱相匹配，然后输入到结构中进行验算（冀昆等，2016）。按PGA对地震动进行调幅之后，相关的幅值参数、频谱参数以及能量参数等都会发生变化。而本文的主要目的是为了研究地震信息参数以及地震动参数等对等强度延性谱的影响，以及调幅之后是否有影响。本文基于Monte Carlo原理从5 500余条地震动记录中随机抽取200条进行研究，分别给出了屈服强度系数Cy为0.3和0.7时，调幅因子不同时平均等强度延性需求谱的变化，以解释等强度延性谱随着调幅因子变化的规律，如图1所示。

由图1可见，对于确定地震动记录，无论调幅因子增大还是减小，其等强度延性谱不会发生变化，与未调幅之前完全重合。所以对等强度延性谱的影响因素进行分析时，可直接选用未调幅的地震动记录进行分析。

2 地震信息参数对等强度延性谱的影响分析

地震信息参数主要包括震中距和震级等，这些因素不同也会使等强度延性谱发生变化。在国内外很多文献中均涉及到当震中距和震级不同时对等强度延性谱影响的研究（周定松，2004;Zhai et al，2017）。为了研究地震信息参数对等强度延性谱的影响，本文将5 500余条地震动按美国USGS场地分类方法，划分为A，B，C，D共4类场地，在场地分类基础上根据震中距和震级再次细分，其分类情况如表1所示。

2.1 震中距对等强度延性谱的影响分析

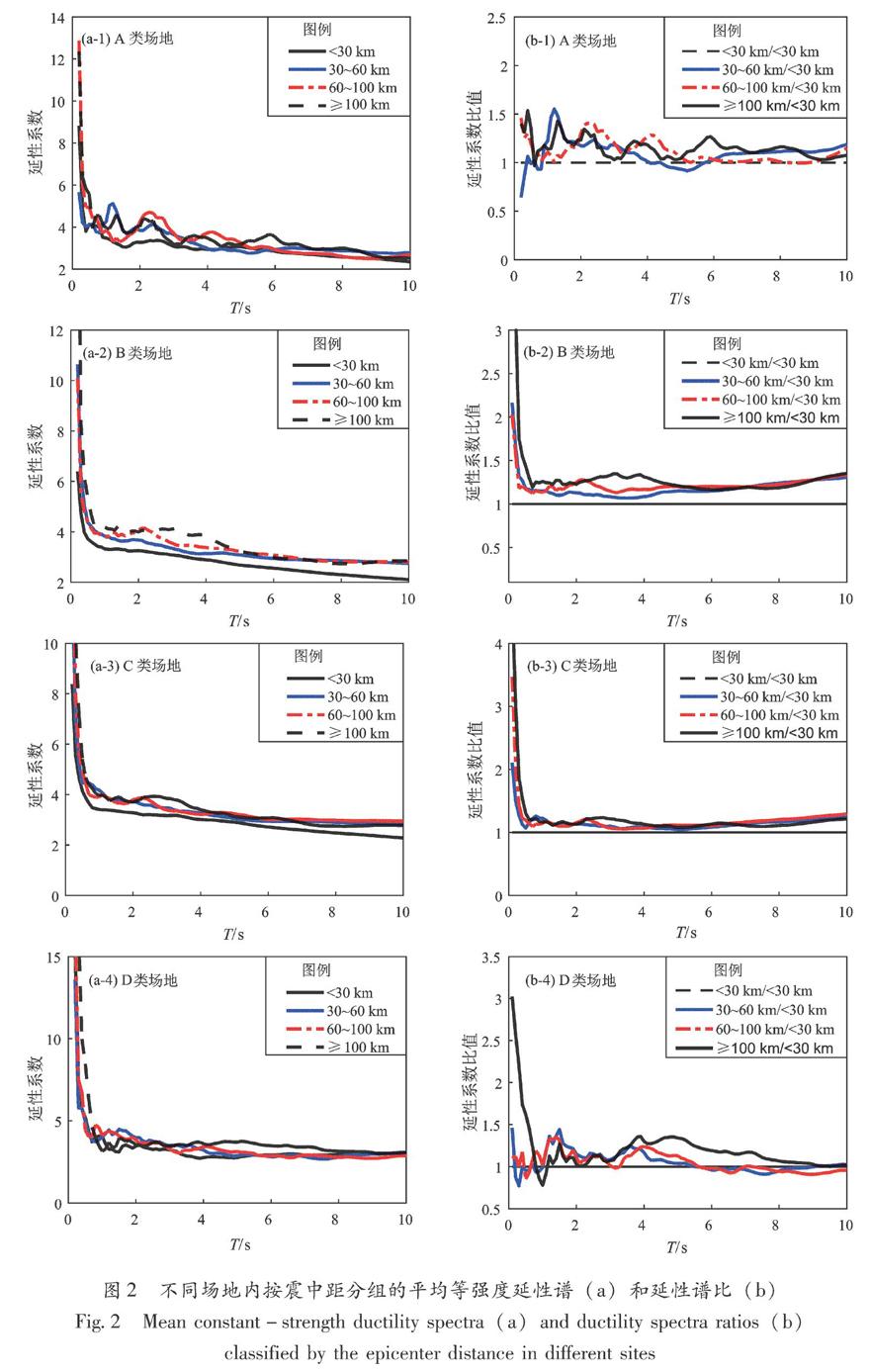
为了研究震中距对等强度延性谱的影响，本文在场地分类的基础上按震中距大小将地震动记录划分为4组，其中第1组震中距小于30 km，包含了较多的脉冲型地震动。分析了屈服强度系数为0.3时，震中距不同时平均等强度延性谱变化规律，如图2a所示;计算得到不同分组与第1组的谱比，如图2b所示。

由图2可见，各组平均等强度延性谱有明显差异。震中距越小，这种变化趋势越明显，震中距大于30 km的平均等强度延性谱值明显大于震中距小于30 km的。总体来说，在所有周期范围内，当震中距越远时，平均等强度延性谱值一般较大;相反，当震中距越近时，平均等强度延性谱值相对较小，这种变化趋势在B，C场地表现较为明显，在A，D类场地内表现较弱。

2.2 震级对等延性强度谱的影响分析

为了研究震级对等强度延性谱的影响，在场地分类的基础上，按震级大小将地震动记录分为4组，其分组情况如表1所示。地震震级不同时平均等强度延性谱变化规律如图3a所示;得到不同分组与第1组谱比，如图3b所示。

由图3可见，将地震动记录按震级大小分组之后，在各分组内分别计算平均等强度延性谱，各平均等强度延性谱呈现明显差异，震级小于5级时得到的平均等强度延性谱值明显小于震级大于5级时得到的;总体上，震级越大，得到的平均等强度延性谱值越大，这一规律除在D类场地长周期范围不明显，在其他场地内都比较明显。与震中距分组相比，根据震级分组规律性更明显一些。

3 地震动参数对等强度延性谱影响分析

结构的弹塑性反应与地震动本身的性质密切相关，地震动记录本身的性质主要从幅值、频谱和持时方面体现。因此本文分别选取了地震动峰值速度（PGV）、有效峰值加速度（EPA）以及Bolt持时进行分析。PGV是由地震动直接得到的参数;Bolt持时是指地震动记录的加速度绝对值首次和末次超过阈值所经历的时间，本文阈值取50 gal;EPA的计算如下：

EPA=S_a/2.5（1）

式中：Sa是阻尼比为5%的加速度反应谱在周期0.1～0.5 s之间的平均值。分别按照3个参数进行分组，得到各组的平均等强度延性谱以及不同分组与第1组比值，如图4所示。

由图4可见，根据地震动参数分组时，分组规律最明显的地震动参数为PGV，其次是Bolt持时，分组规律最不明显的为EPA。平均等强度延性谱与PGV和Bolt持时有较好的正相关性，PGV和Bolt持时越大，平均等强度延性谱值越大，然而当Bolt持时大于20 s时，Bolt持时与平均等强度延性谱值规律不再明显。

延性系数随着EPA的变化没有明显规律。但是可以看出在较短周期时，EPA大于40 gal时计算得到的延性需求小于EPA小于40 gal时计算所得到的;而在中长周期时，EPA大于40 gal时计算得到的延性需求大于EPA小于40 gal时计算所得到的。

4 结论与讨论

为了分析地震信息参数和地震动参数对等强度延性谱的影响，将地震动记录按地震信息参数和地震动参数分组，研究各组间平均等强度延性谱的变化规律。从NGA-West2数据库中选取了5 500条水平向地震动记录计算平均等强度延性谱，主要得到以下结论：

（1）无论是根据地震信息参数分组，还是根据地震动参数分组，建立的等强度延性谱都会有明显的差异，因此等强度延性谱受多个因素影响。

（2）在场地分类的基础上，根據震中距和震级对地震动记录分组，分析不同分组平均等强度延性谱的变化。在大多数周期范围内，当震中距大于30 km时，平均等强度延性谱值明显大于震中距小于30 km时所得到的，B，C场地内该规律尤为明显;当震级越大时，得到的平均等强度延性谱值较大，当震级越小时，得到的平均等强度延性谱值越小。

（3）根据地震动参数分组时，按照PGV，EPA以及Bolt持时对将地震动记录进行分组。按PGV分组时与平均等强度延性谱有很好的正相关性，其次为Bolt持时，根据EPA分组时变化规律最不明显。

因此，在基于强地震动记录建立等强度延性谱时需要考虑震中距、震级和PGV等多个参数的综合影响。

感谢PEER发布的NGA-West2数据库为本研究提供数据支持。

参考文献：

何海健，徐孟豪，苏亮，等.2018.结构弹塑性时程分析中输入地震动的选取数量研究[J].地震工程与工程振动，38（2）：150-156.

冀昆，温瑞智，任叶飞.2016.中国抗震规范强震记录选取的初选条件研究[J].防灾减灾工程学报，36（1）：44-49.

薛尚铃，余周，徐革，等.2017.银川德丰大厦弹塑性动力时程分析[J].建筑结构，（5）：37-42.

易伟建，张海燕.2005.弹塑性反应谱的比较及其应用[J].湖南大学学报，32（2）：42-45.

翟长海，李爽，谢礼立，等.2008.近场脉冲型地震动位移比谱特征研究[J].土木工程学报，41（10）：1-5.

翟长海，谢礼立，张茂花.2006.阻尼对工程结构等延性地震抗力谱的影响分析[J].哈尔滨工业大学学报，38（10）：1705-1708.

周定松.2004.考虑场地类别与设计分组的延性需求谱和弹塑性位移反应谱[J].地震工程与工程振动，24（1）：39-48.

Chopra A K.2007.Dynamics of Structures：Theory and Applications to Earthquake Engineering[M].California：Earthquake Engineering Research Institute.

Miranda E.1993.Evaluation of Site‐Dependent Inelastic Seismic Design Spectra[J].Journal of Structural Engineering，119（5）：1319-1338.

Newmark N M，Hall W J.1969.Seismic design criteria for nuclear reactor facilities[J].Building Practices for Disaster Mitigation，4（2）：37-50.

Xie L L，Zhai C H.2003.Study on the severest real ground motion for seismic design and analysis[J].Acta Seismologica Sinica，16（3）：260-271.

Zhai C，Ji D，Wen W，et al.2017.Constant Ductility Energy Factors for the Near-Fault Pulse-Like Ground Motions[J].Journal of Earthquake Engineering，21（2）：343-358.

Zhai C，Li S，Xie L，et al.2007.Study on inelastic displacement ratio spectra for near-fault pulse-type ground motions[J].Earthquake Engineering and Engineering Vibration，6（4）：351-355.

Analysis of Influencing Factors on the Constant-strength Ductility Spectrabased on the Strong Ground Motions

LAI Qinghui，HU Jinjun，LIU Xuan，XIE Lili

（Key Laboratory of Earthquake Engineering and Engineering Vibration，Institute of Engineering Mechanics，China Earthquake Administration，Harbin 150080，Heilongjiang，China）

Abstract

To study the effect of different factors on the constant-strength ductility spectra，based on more than 5500 horizontal ground motion data with peak ground acceleration greater than 50 gal，the elastoplastic response of single degree of freedom system（SDOF）is calculated by bilinear model，and the factors affecting the constant-strength ductility spectra are analyzed mainly from the aspects of seismic information parameters and ground motion parameters.First，in the analysis of seismic information parameters，ground motions are grouped according to the epicenter distance and magnitude on the basis of site classification，and the effects of epicenter distance and magnitude on the constant-strength ductility spectra are analyzed.Second，in terms of ground motion parameters，the representative parameters reflecting amplitude，frequency spectrum and duration，such as peak ground velocity（PGV），effective peak acceleration（EPA）and Bolt duration，are analyzed，and their effects on constant-strength ductility spectra are analyzed by grouping them according to the magnitude of PGV，EPA and Bolt duration.The results show that：①In most of the periods，there is a greater difference in the constant-strength ductility spectra of each group，and when the epicenter distance and magnitude are larger in each site，the corresponding ductility spectrum values are larger.②The best grouping effect is PGV，followed by Bolt duration.When grouped according to EPA，the grouping result is the most unsatisfactory.Therefore，when establishing constant-strength ductility spectra based on the strong ground motion records，it is necessary to consider the comprehensive effects of epicenter distance，magnitude，PGV and other parameters.

Keywords：ground motion parameters;constant-strength ductility spectra;inelastic response;influencing factors