超长混凝土单跨梁曲线预应力筋参数影响分析
杨寒 李志黎


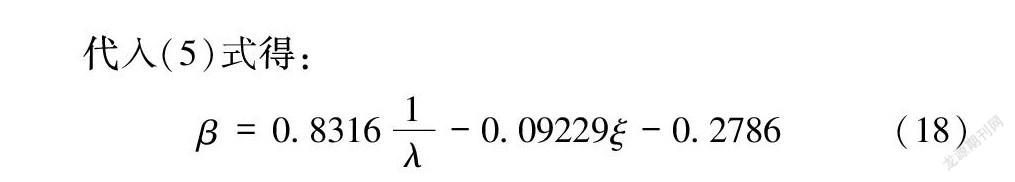



[摘 要]:曲线预应力筋矢高与预应力度对超长混凝土单跨梁的裂缝宽度、承载力和延性均有影响。文章为探究其在超长混凝土单跨梁中的合理设置,通过弯矩二次分配法,推导在二级和三级裂缝控制等级下预应力筋矢高比的表达式,得到了预应力筋矢高设计下限值,并结合某车站工程单跨预应力梁截面设计,利用XTRACT软件进行参数分析。结果表明:矢高比越大,截面延性系数越大、承载力越小;当矢高比小于0.61时,截面极限弯矩随预应力度增大而增大,当矢高比大于0.61时,截面极限弯矩随预应力度增大而减小。
[关键词]:矢高比; 预应力度; 极限弯矩; 延性
TU378.2A
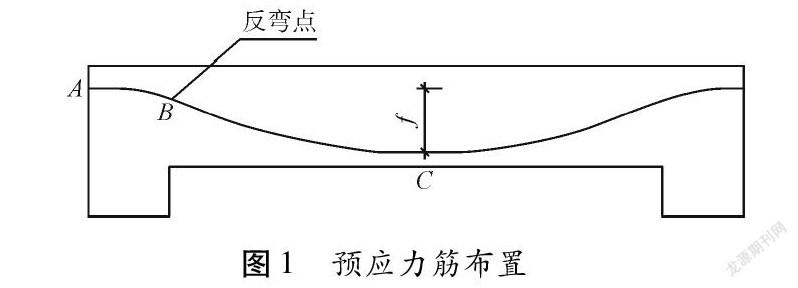
在预应力结构设计中,预应力筋外形和位置设计对结构的抗震性能具有显著影响。理论上,预应力筋线形布置应与均布荷载作用下的弯矩分布图一致,但是为了施工方便,使端部锚具垂直于截面,多数大跨工程采用多波曲线预应力筋的线形布置[1](图1)。关于预应力筋位置,杨建明等[2]建议梁端预应力筋应尽量下移,同时考虑降低预应力筋矢高对梁承载力带来的不利影响;王新玲等[3]基于预应力混凝土构件在施工阶段预拉区的抗裂要求,推导了预应力筋布置偏心距的表达式,以此作为超静定梁预应力筋布置的依据。
为综合考虑预应力筋位置及预应力度对混凝土梁裂缝、承载力以及延性的影响,本文以预应力筋矢高作为参考量,基于裂缝控制等级条件和梁截面极限承载力推导预应力筋矢高比关于预应力度和截面相对受压区高度的关系式,根据规范[4-5]中预应力度和截面相对受压区高度限值要求,计算得到预应力筋矢高比下限值,并利用XTRACT软件对预应力梁梁端截面进行计算,分析预应力筋矢高与预应力度对预应力梁截面延性及承载力的影响规律。
1 参数定义
大跨预应力梁预应力筋布置如图1所示,A点和C点之间的垂直距离为矢高。
定义预应力筋矢高比:
β=f/h(1)
式中:f为预应力筋矢高;h为梁截面高度。
文献[6]指出预应力度λ对预应力混凝土框架抗震性能有直接影响并对其限值进行了规定。为简化计算,根据文献[7]取λ=Apfpy/(Apfpy+Asfy),其中,Ap、As分别为预应力筋和普通钢筋面积,fpy、fy分别为预应力筋和普通钢筋屈服强度。
2 预应力筋矢高下限值推导
预应力混凝土梁的设计,需首先满足抗裂要求,确定预应力筋用量[8]。以下从理论上分析裂缝控制等级分别为三级和二级时预应力筋用量,再从截面极限承载能力的角度确定预应力用量,并结合单跨预应力梁内力与预应力筋矢高的关系,推导曲线预应力筋矢高比表达式,进一步确定矢高比下限值。
2.1 单跨预应力梁内力表达式
根据文献[9]推导出的单跨预应力混凝土框架次弯矩简化计算方法,并结合文献[10]对梁柱线刚度比的研究,取梁柱线刚度比1.5,分别得到梁的次弯矩M2和综合弯矩Mr:
M2=47(23β-γ-13αβ)Nh(2)Mr=(37γ+1721αβ+821β)Nh(3)
式中:γ为预应力筋偏心距与截面高度比;α为预应力筋反弯点到支座距离与跨长的比值;N为预拉力。
令:
ωr=37γ+1721αβ+821β(4)
ω2=47(23β-γ-13αβ)(5)
则次弯矩和综合弯矩可分别简化为:M2=ω2Nh;Mr=ωrNh。
2.2 预应力筋矢高比表达式
2.2.1 三级裂缝控制
目前,使用纵向受拉钢筋的等效应力σsk估算预应力筋数量并进行裂缝宽度控制的方法应用广泛[11]。有相关研究[12]发现:当σsk≤190 MPa其最大裂缝宽度总能控制在0.2 mm以内,有学者对规范中σsk的计算方法进行简化[7],得到表达式:
σsk=N(e-z)(Ap+As)z(6)
N=σpeAp(7)
z=0.87-0.12(1-γ′f)(h0e)2h0(8)
e=ηse0+ys(9)
e0=Mk-MrN(10)
式中:σpe为预应力钢筋有效预应力;e为轴向压力作用点至纵向受拉钢筋合力作用点的距离;e0为初始偏心距;z为纵向受拉钢筋合力作用点至受压区合力作用点的距离;ηs为使用阶段的轴向压力偏心距增大系数;ys为截面重心至纵向受拉钢筋合力作用点的距离;Mk为外荷载作用下的弯矩。
工程结构杨寒,李志黎: 超长混凝土单跨梁曲线预应力筋参数影响分析
取极限值σsk=190 MPa,得到三级裂缝控制等级下预应力筋用量:
Ap=Mkσpeh0.516781λ-0.02023+ωr(11)
由承載能力极限状态计算预应力筋用量[8]:
Apu=Mufpy·1γsh0+1λ-1h0-α′s(12)
式中:γs为截面力矩系数;h0为截面有效高度;α′s为受压钢筋压应力合力作用点至截面受压边缘距离;Mu为截面极限弯矩。
构件配筋同时满足抗裂要求和承载力要求时,Apu=Ap,依据文献[13]取Mu/Mk=1.25,σpe=1000MPa ,fpy=1320MPa,γ=0.35,h0-α′s=0.95 h0,α=0.2,γs=1-0.5ξ,ξ=x/0.9h[7],联立解得:
ωr=0.357411λ-0.4752ξ+0.06775 (13)
代入式(4)得:
β=0.658391λ-0.87537ξ-0.15151(14)
2.2.2 二级裂缝控制
有学者推导二级裂缝控制等级预应力混凝土构件在极限状态下内力表达式[8]:
Mk=2Nepn+M2(15)
式中:epn为净截面重心至预应力作用点距离。
将式(2)代入式(15)中计算得:
Ap=Mk2σpeepn+αβh+ω2h(16)
依据文献[7]取γsh0/epn=0.24,Mu/Mk=1.25,σpe=1000MPa ,fpy=1320MPa,同理联立式(12)和式(14),并取γs=1-0.5ξ,计算得:
ωr=0.451441λ-0.0501ξ-0.35124-0.2β(17)
代入(5)式得:
β=0.83161λ-0.09229ξ-0.2786(18)
2.3 矢高比下限值
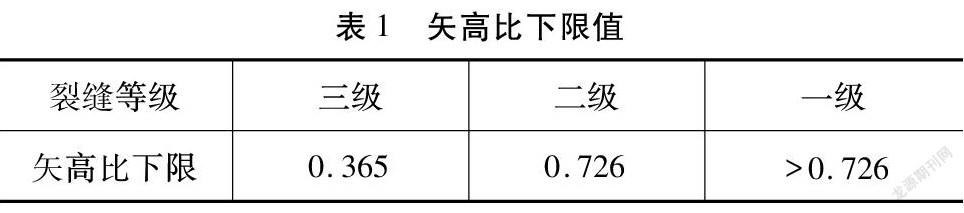
由式(14)和式(18)可知,在三级裂缝和二级裂缝控制等级下,预应力筋矢高比随着预应力度或截面相对受压区高度增加而降低,GB 50011-2010《建筑抗震设计规范》[4]指出,二级和三级抗震等级条件下,截面相对受压区高度ξ上限值为0.35。由文献[6]知,二级至四级抗震等级条件下,预应力度λ上限值为0.8。由此,将规范限值代入式(14)和式(18),计算曲线应力筋矢高比下限值如表1所示。
3 梁截面受力性能分析
由表1知一级与二级裂缝等级要求矢高比β≥0.726,而矢高比过大引起的次弯矩对结构的不利影响往往不容忽视,且考虑到预应力度限值,裂缝等级宜尽量采用允许出现裂缝的三级[5]。故以下探讨三级裂缝控制等级下,预应力筋矢高与预应力度对单跨梁极限承载力与延性的影响。结合某车站工程,其顶层为单跨结构,跨度22.8 m,混凝土强度等级C40,有粘结预应力筋,抗拉强度标准值:1 860 MPa,控制应力1 320 MPa,截面参数设置见图2,利用XTRACT软件对其梁端截面进行计算分析。
3.1 截面延性分析
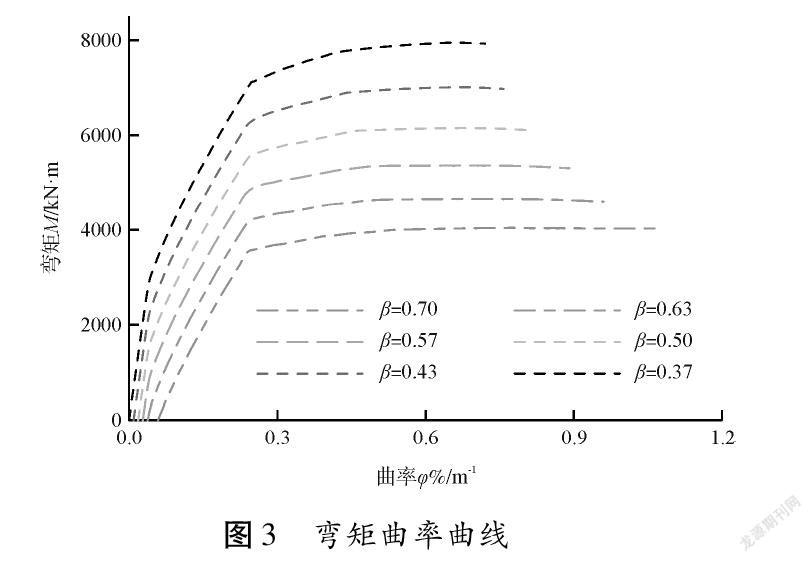
由图2配筋知,截面预应力度为0.746,改变预应力筋位置,并保持其他参数不变,设置预应力筋矢高比分别0.7、0.63、0.57、0.50、0.43、0.37,得到不同梁端截面弯矩-曲率曲线(图3)。
由图3知,矢高比从0.7降低到0.37,对应的极限曲率值分别为1.064% m-1、0.96% m-1、0.89% m-1、0.81% m-1、0.76% m-1、0.70% m-1,极限弯矩值分别为4 026 kN·m、4 600 kN·m、5 305 kN·m、6 104 kN·m、6 976 kN·m、7 928 kN·m,即随着预应力筋矢高比的降低,截面变形能力不断下降,弯矩承载力不断上升。
为评价预应力梁梁端截面延性性能,本文将曲率延性系数μ定义为:
μ=(φu-φ0)/(φy-φ0)(19)
式中:φu为极限曲率,1/m;φy为屈服曲率,1/m;φ0为初始曲率,1/m。
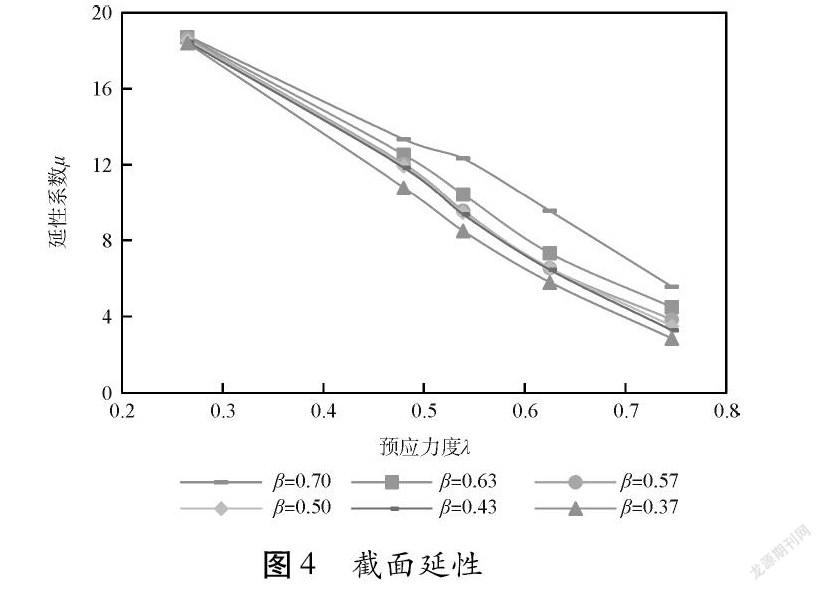
设计5组不同预应力度的截面(分别为0.746、0.625、0.539、0.48、0.265),每组截面含6种矢高比(分别为0.7、0.63、0.57、0.5、0.43、0.37),截面延性系数与预应力度的关系如图4所示。
由图4知,截面延性随预应力度呈显著线性变化,预应力度越大,延性系数越小,随着预应力筋矢高比的增加,截面延性系数随之增加;延性系数呈斜锐角三角形分布,锐角度越小,矢高比对截面延性影响越小,为比较预应力度与预应力筋矢高比对截面延性系数的影响程度,定义延性系数平均增幅比i:
φi=Δφm/Δi(19)
式中:Δφm为参数i对应的延性系数平均值差;Δi为参数i区间长度。
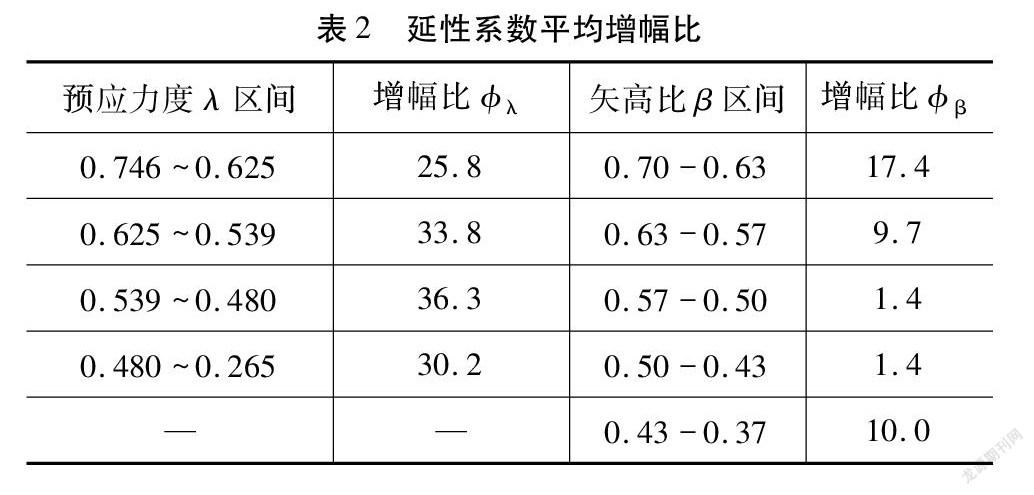
各参数不同区间截面延性系数平均增幅比如表2所示。
由表2知,预应力度对截面延性系数的影响程度明显大于预应力筋矢高比,故对截面延性进行优化设计时,优先考虑降低预应力度,其次再增加预应力筋矢高比。
3.2 截面承载力分析
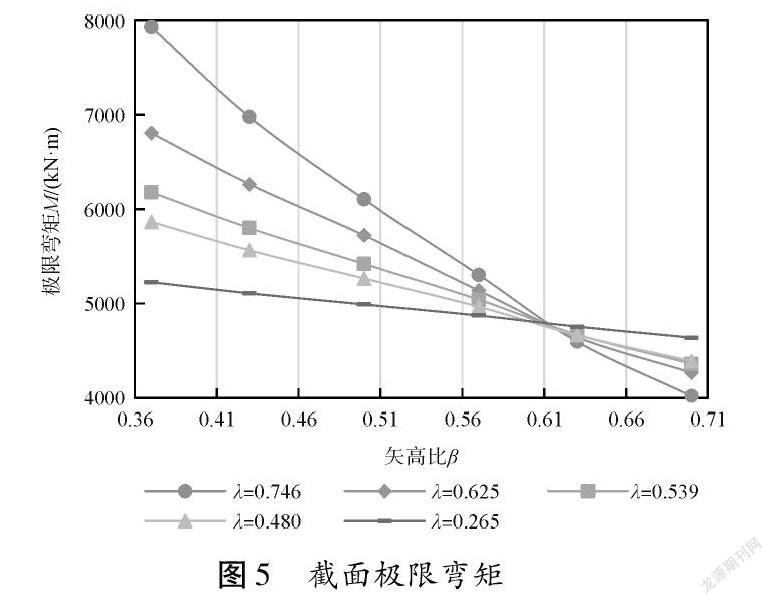
为综合评价预应力矢高比与预应力度对单跨预应力梁承载力的影响,分析不同预应力度对应的预应力矢高比与极限弯矩关系,结果如图5所示。
截面极限弯矩呈对角三角形分布,极限弯矩随矢高比增加而减小,矢高比为0.37、0.43、0.5、0.57时,截面极限弯矩随预应力度增加而增加,矢高比为0.63、0.7时,截面极限弯矩随预应力度增加而减小。定义临界矢高比βc,当β=βc时,截面极限弯矩不受预应力度变化的影响,由图5知,βc≈0.61,即当β>0.61时,可适当减小预应力度以保证截面承载力。
4 结论
本文基于裂缝控制等级和梁截面极限承载力推导超长混凝土单跨梁曲线预应力筋矢高比的表达式,并利用XTRACT软件对梁端截面进行计算分析,得到总结:
(1)三级裂缝控制等级下,曲线预应力筋矢高下限值为0.37倍截面高度,二级裂缝控制等级下,曲线预应力筋矢高下限值为0.72倍截面高度。
(2)截面延性随矢高比增大而增大、随预应力度增加而减小,承载力随矢高比增加而减小,且矢高比对截面延性的影响程度小于预应力度、对弯矩承载力的影响程度大于预应力度。
(3)预应力梁截面存在一个弯矩承载力临界矢高比,当设计矢高比大于临界矢高比时,可适当减小预应力度以保证截面承载力。
参考文献
[1] 邱剑, 王东峰, 叶志雄. 预应力筋布置对框架结构设计的影响分析[J]. 建筑结构, 2012(S2):384-387.
[2] 杨建明, 杨宗放. 框架结构中预应力筋合理布置的研究[J]. 建筑结构,1993(1):10-14.
[3] 王新玲, 赵更奇, 杨广宁. 预应力混凝土超静定梁的预应力筋布置分析[J]. 工业建筑,2004(6):39-41.
[4] 建筑抗震设计规范: GB50011-2010[S].北京:中国建筑工业出版社,2010.
[5] 预应力混凝土结构抗震设计标准: JGJ/T140-2019[S].北京:中國建筑工业出版社,2019.
[6] 唐九如, 吕志涛, 张敏. 预应力混凝土延性框架抗震配筋限值研究[J]. 建筑结构学报, 1996(1):20-28.
[7] 张江. 预应力度取值对PC框架结构抗震性能影响的研究[D]. 武汉:华中科技大学,2016.
[8] 张耀庭,张江,杨力. 预应力度对预应力混凝土框架结构抗震性能影响研究[J]. 工程力学,2017,34(2):129-136.
[9] 张玉明, 孟少平. 预应力混凝土框架次弯矩简化计算方法探讨[J]. 工业建筑, 2006(3).
[10] 田北平. 制盐厂房框架柱计算长度的确定及梁柱适宜刚度比[J]. 中国井矿盐, 2002(3).
[11] 于琦, 孟少平. 部分预应力混凝土受弯构件裂缝宽度计算方法探讨[J]. 建筑结构,2009,39(3):31-33.
[12] 谢姣姣垄, 鲁兆红, 张瀑. 预应力混凝土框架梁裂缝控制实用方法的研究[J]. 四川建筑科学研究,2014,40(1):129-131.
[13] 潘其健. 预制预应力混凝土框架结构抗震能力的试验研究[D]. 南京: 东南大学, 2006.

