远场地震作用下累积延性比谱的建立
马翠玲,黄镜渟
(合肥学院城市建设与交通学院,安徽 合肥 230601)
0 引言
地震作为自然灾害之一,对人类危害极大。我国58%的国土面积位于Ⅶ度及以上高烈度区,数次强震均造成了不同程度的财产损失和人员伤亡。
1992年,美国学者提出了基于性态[1]的结构抗震设计理念,随后,国内外学者对此展开了一系列研究,成果颇多[2-15]。基于性态的抗震设计方法,可按大类分为基于位移、基于损伤和基于能量方法等。其中,基于能量方法既可以考虑力与位移两个因素,又兼顾地面运动持时所引起的结构累积损伤,概念清晰,因此该方法自Housner于1956年提出以来便迅速成为研究热点,并取得了不少成果[16-17]。
承受底部激励的单自由度体系能量方程为:
(1)
式(1)可写为:
Ekr+ED+EE+EH=Elr
(2)
式中:Ekr为动能;ED为阻尼能;EE为弹性应变能;EH为滞回耗能;Elr为输入能。
作为远场地震作用下结构塑性累积损伤的主要指标,结构的累积滞回耗能与结构单调推覆耗能并不对应,因此,基于能量的性态设计方法需要研究二者之间的关系。
Akbas等[18]研究了结构基本周期与总输入能、滞回耗能、阻尼能的图解关系文献,建立了结构累积滞回耗能需求与累积耗能间的关系。Choi等[19]将滞回耗能谱、累积延性谱用于屈曲约束支撑钢框架基于能量的设计,用20条地震波建立了滞回耗能谱和累积延性谱。Kim等[20]基于滞回耗能谱、累积延性比谱提出了屈曲约束支撑钢框架结构的能量抗震设计方法。孙国华等[21]引入累积延性比,建立了标准化滞回耗能谱、累积延性比谱,但谱的场地类别划分与我国抗震规范不对应。文献[22-24]利用文献[21]的标准化滞回耗能谱、累积延性比谱,分别对远场地震下K型偏心支撑钢框架、抗弯钢框架、人字形中心支撑钢框架进行了基于能量设计方法的研究。
本文选取按中国场地分类的750条远场水平地震记录,按照中国抗震规范的场地类别划分、设计地震分组对其进行了分类,得到15组地震记录。根据给定的结构恢复力模型、目标延性系数μ,通过不断改变单自由度(single degree of freedom, SDOF)体系的周期T,获得在目标延性下结构的累积延性比RH谱的数学表达式。
1 累积延性比谱影响因素分析
结构耗散的滞回耗能取决于其所经历的塑形变形,结构在远场地震作用下由于无规律的往复侧移形成的累积延性可以通过累积延性比谱表征。累积延性比RH可视为结构经历的所有塑性变形与结构屈服侧移之比,其定义见式(3)。
(3)
式中:EH为结构的累积滞回耗能;Fy为结构的屈服承载力;dy为结构的屈服侧移。
本节分析场地类别、地震波幅值、设计地震分组和结构阻尼比、延性系数、后期刚度对累积延性比谱的影响。考虑到地震的离散性和随机性,本文延性比值采用大样本地震波所获结果的平均值。
1.1 谱分析参数
以弹塑性SDOF体系为研究对象,选用双线性恢复力模型,后期刚度p取值为0、0.02、0.05、0.10、0.20、0.50,结构阻尼比ζ取值为0.01、0.02、0.035、0.05、0.10、0.20,延性系数μ取值为2、3、4、5、6、7、8。
1.2 场地类别的影响
利用谱分析软件可以得到,不同类别场地下,延性系数μ=3、后期刚度p=0.05、阻尼比ζ=0.05的弹塑性SDOF体系当地震波幅值PGA(峰值加速度,peak ground acceleration)为0.2g时对应的累积延性比谱如图1所示。由图1可知,随着场地类别的变化,累积延性比谱的形状和数值均有所变化。从谱形状上分析,Ⅱ类场地累积延性比谱最为平滑,Ⅳ类场地累积延性比谱较为离散,Ⅰ类(含Ⅰ0和Ⅰ1两个亚类)、Ⅲ类场地累积延性比谱形状离散程度介于二者之间,这应该与各类场地所选用的地震波的样本空间不同有关,Ⅳ类场地地震波数量相对偏少。从谱值上分析,在周期全长范围内,各类场地的谱值上下浮动较小,故下文以不同周期下各谱值的平均值为代表来考虑场地类别的影响。其中,Ⅱ类场地累积延性比谱值最小,Ⅳ类场地累积延性比谱值最大,Ⅰ类(含Ⅰ0和Ⅰ1两个亚类)、Ⅲ类场地累积延性比谱值介于二者之间。

图1 场地类别对累积延性比谱的影响(μ=3,p=0,ζ=0.05)
1.3 幅值的影响
为了考察地震波幅值对累积延性比的影响,选择阻尼比为0.05、延性系数为3、后期刚度为0.1、双线性恢复力模型的弹塑性SDOF体系为研究对象,选取不同场地类别不同设计分组的2条地震记录RSN2358E和RSN5608E输入谱分析软件中,数据处理后得到幅值分别为0.2g、0.4g和0.52g时的累积延性比谱,如图2、图3所示。
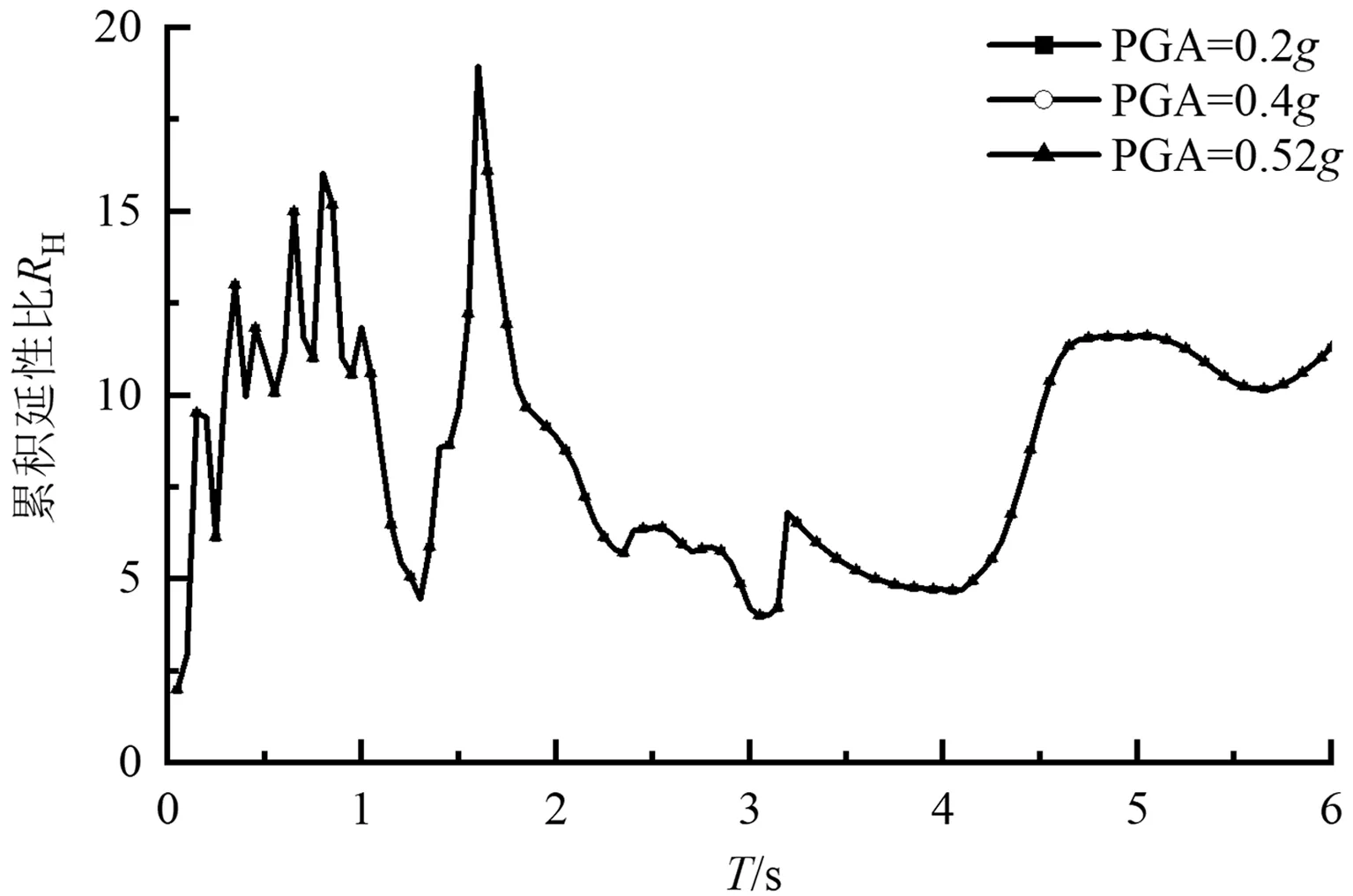
图2 地震波RSN2358E作用下加速度峰值不同时的累积延性比谱(μ=3,p=0.1,ζ=0.05)
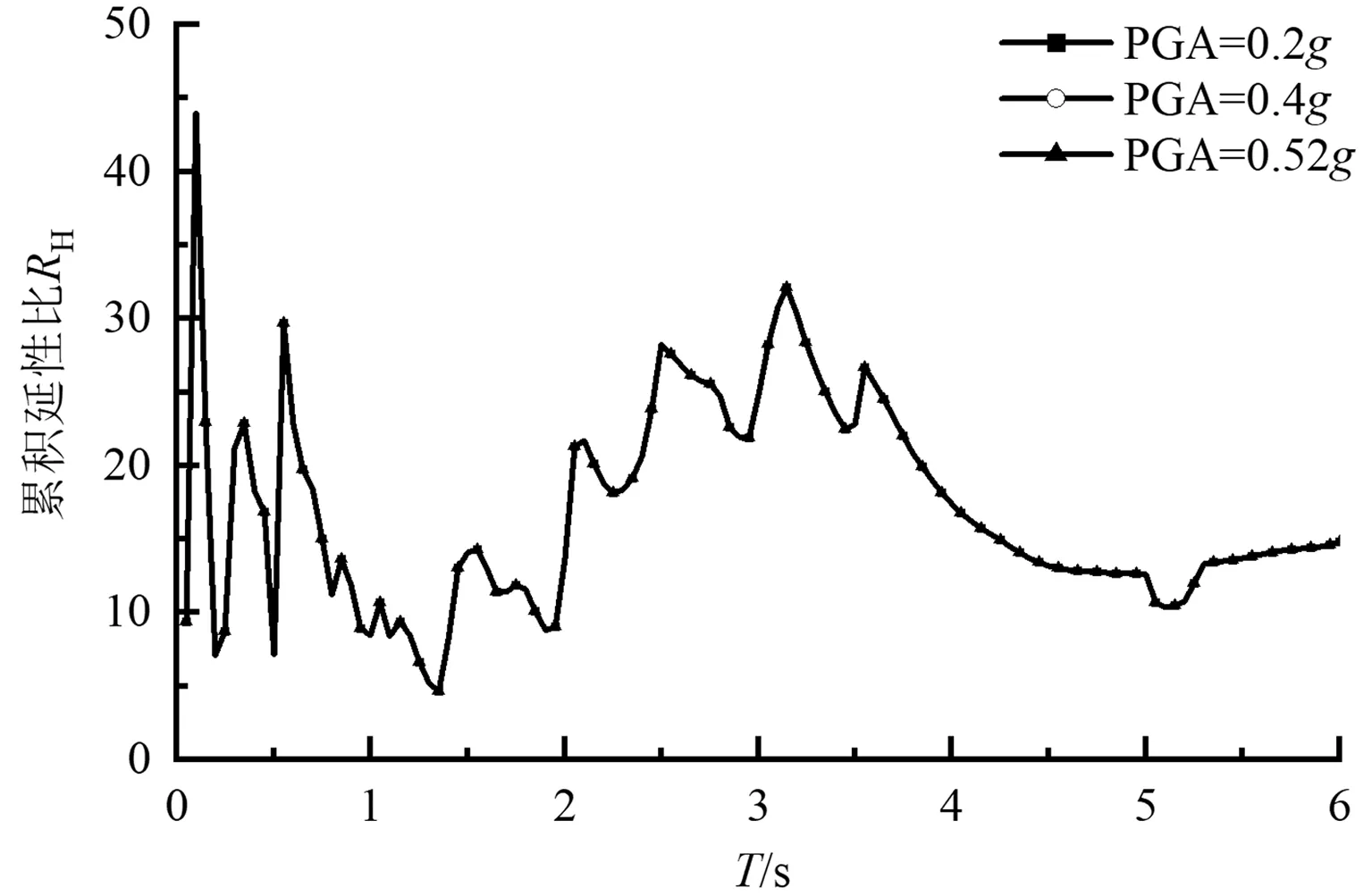
图3 地震波RSN5608E作用下加速度峰值不同时的累积延性比谱(μ=3,p=0.1,ζ=0.05)
由图2、图3可以看出,随着加速度幅值的增大,在周期全长范围内累积延性比谱重合,其形状及数值均不变,即地震波幅值大小对累积延性比谱没有影响,因此下文在归纳分析累积延性比谱的数学表达式时不需要考虑幅值参数。
1.4 频谱特征的影响
地震波的频谱特征可通过设计地震分组表征。分析时,选用延性系数为3、后期刚度为0.05、阻尼比为0.05的弹塑性SDOF体系为研究对象,利用谱分析软件可得到Ⅱ类场地对应不同设计地震分组时累积延性比谱,如图4所示。

图4 设计地震分组对累积延性比谱的影响
由图4可知,设计地震分组对累积延性比谱有一定影响,其中,第二组对应的谱值比第一组、第三组普遍偏大;第三组累积延性比谱最为平缓,其次是第一组、第二组。当结构周期T不小于0.5 s时,在同一周期下,第三组与第一组对应的谱值之比介于0.95~1.20,所有比值的平均值为1.04;第二组与第一组对应的谱值之比介于0.93~1.52,所有比值的平均值为1.20。
1.5 阻尼比的影响
为了考察阻尼比对累积延性比谱的影响,选择延性系数分别为4、6、8,后期刚度为0,阻尼比分别为0.01、0.02、0.035、0.05、0.10和0.20的弹塑性SDOF体系,恢复力模型选择双线性,采用Ⅱ类场地第一、二、三组所有地震记录PGA调幅为0.2g后作为地震波输入,利用谱分析软件得到结构阻尼比变化时的累积延性比谱,如图5所示。

(a)第一组,μ=4,p=0

(b)第一组,μ=6,p=0

(c)第一组,μ=8,p=0
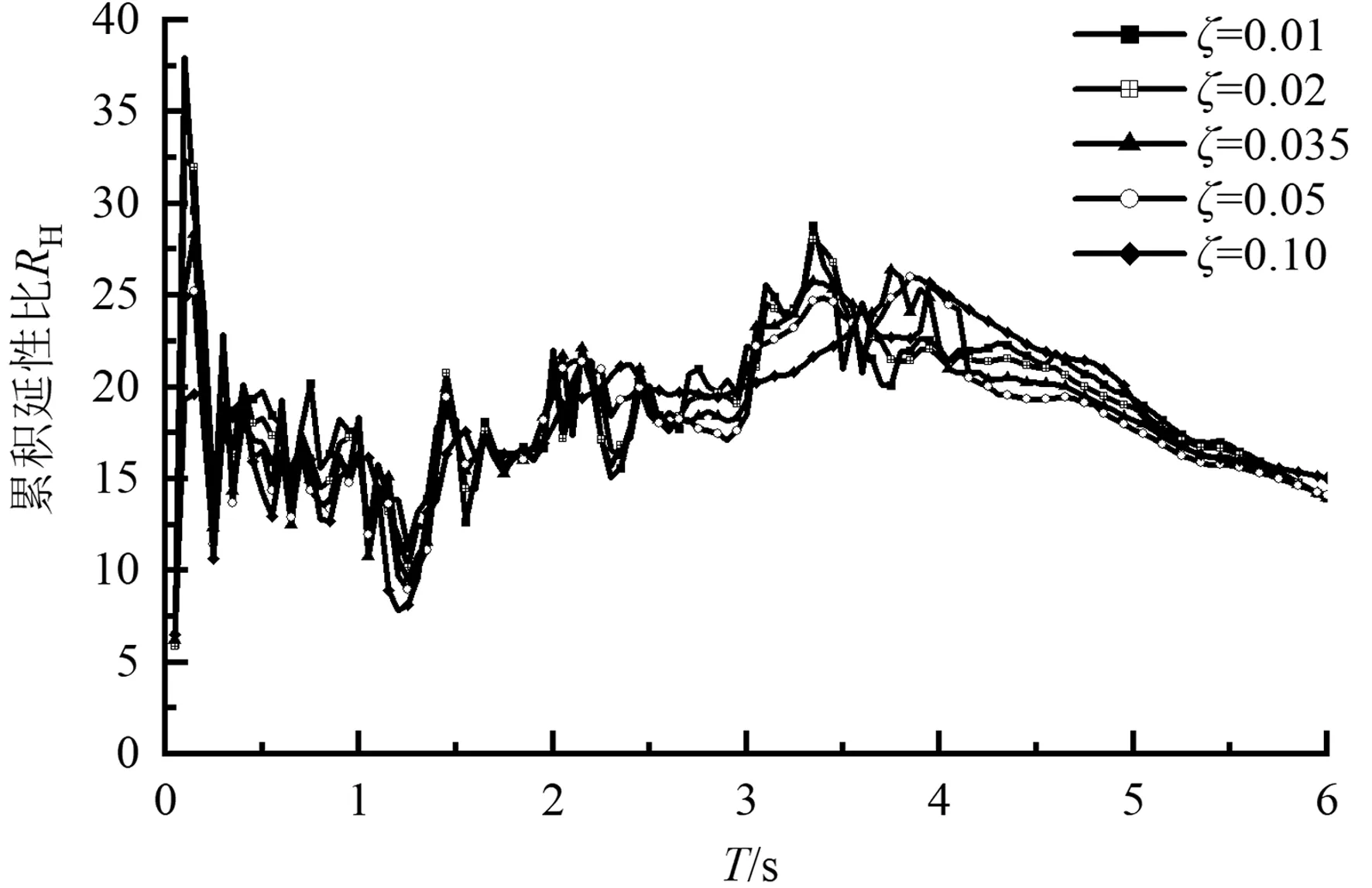
(d)第二组,μ=4,p=0
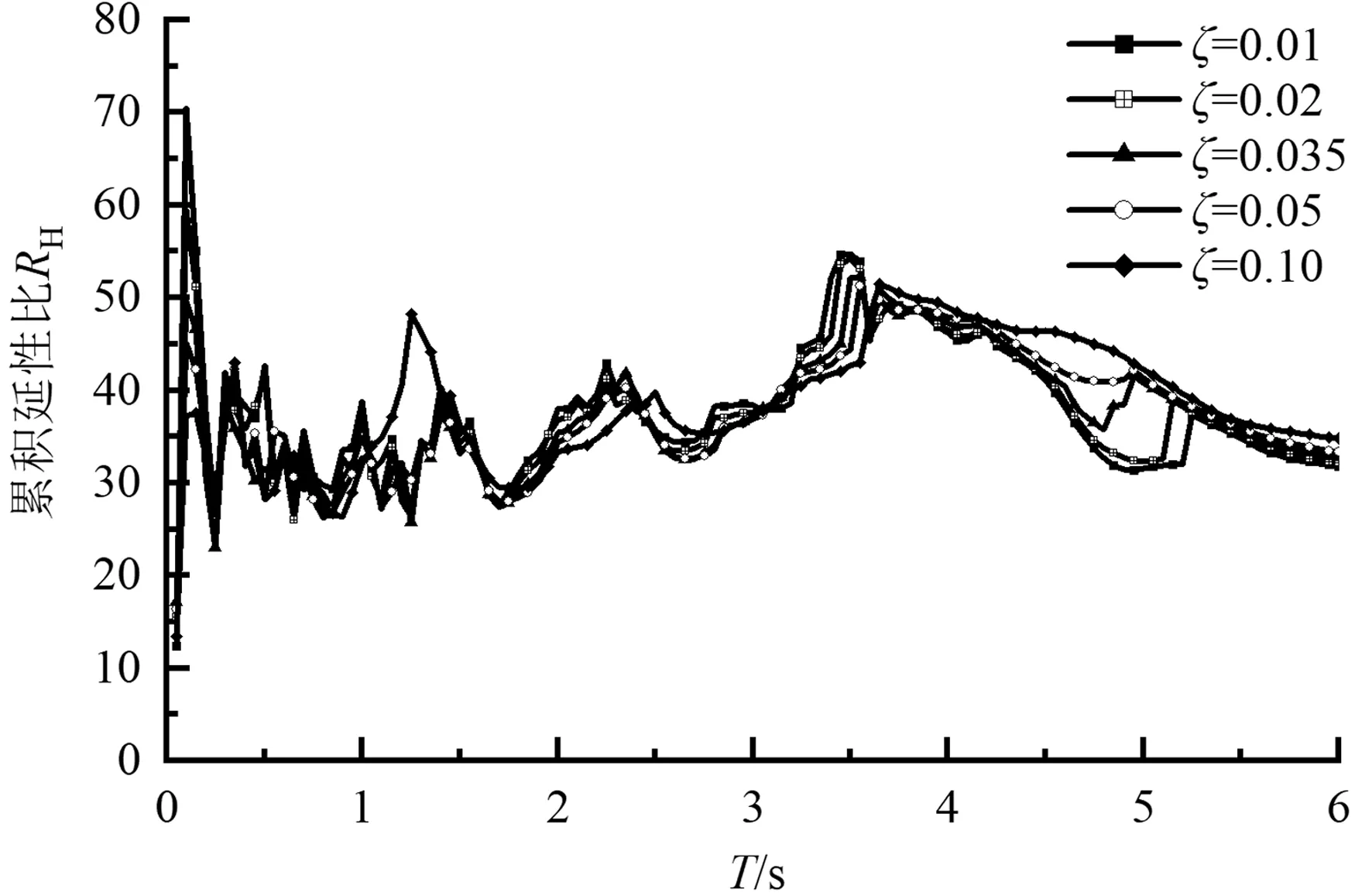
(e)第二组,μ=6,p=0

(f)第二组,μ=8,p=0

(g)第三组,μ=4,p=0
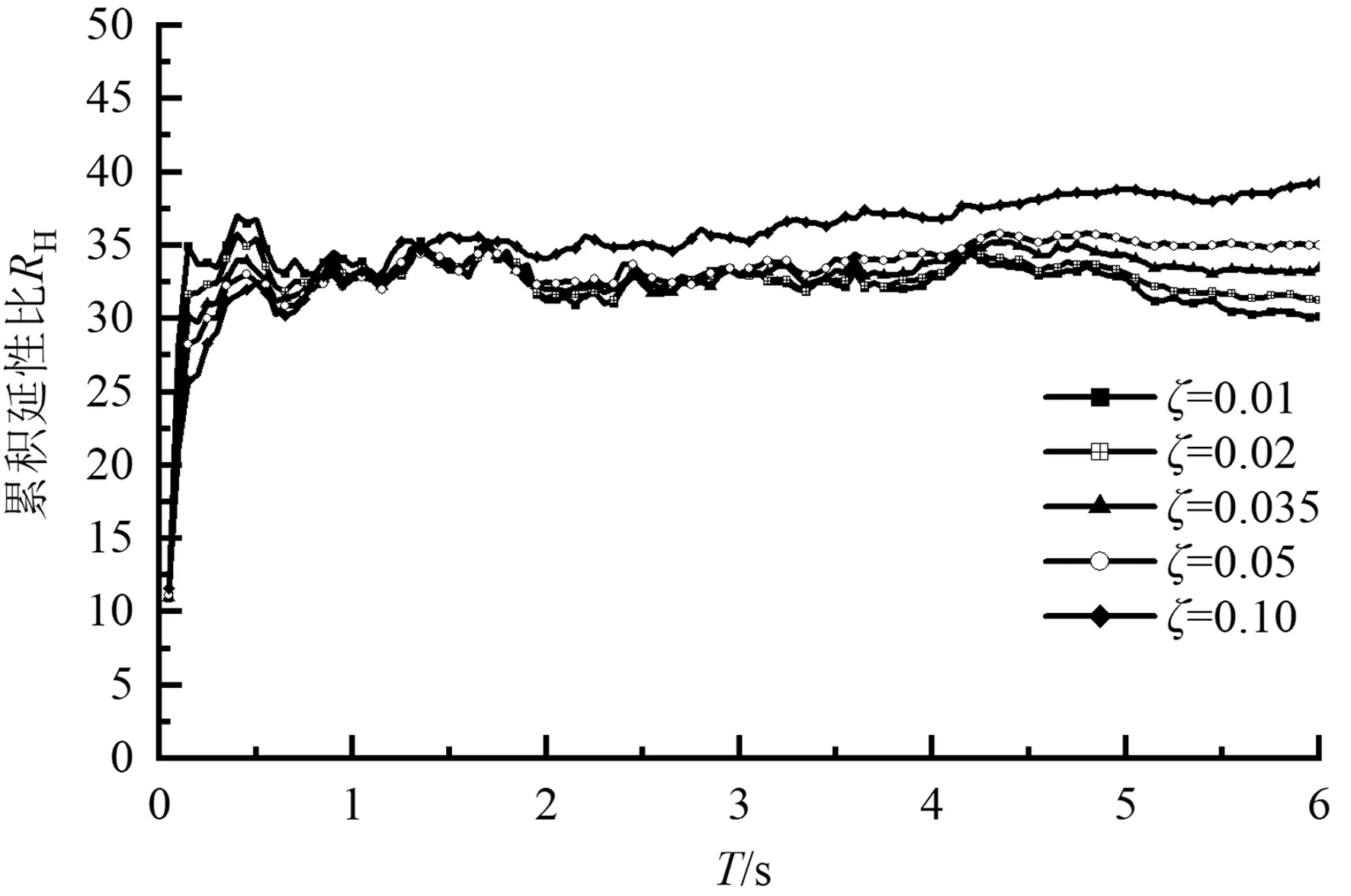
(h)第三组,μ=6,p=0

(i)第三组,μ=8,p=0图5 阻尼比对累积延性比谱的影响
观察图5可以得到,累积延性比谱随阻尼比的增加而趋于平滑。当延性系数增加时,阻尼比的影响更为明显,体现了延性系数对累积延性比谱的影响不可忽略。同时,当设计地震分组为第一、三组时,当阻尼比分别为0.01、0.02、0.035时累积延性比较稳定,当阻尼比为0.05、0.10、0.20时累积延性比呈轻微增大趋势,尤其是中长周期范围内,但增大幅度有限。
1.6 延性系数的影响
延性系数反映了结构的非线性特性,其对累积延性比谱有影响。为了考察延性系数对累积延性比的影响规律,选择阻尼比为0.05、后期刚度为0.05的弹塑性SDOF体系为研究对象,以Ⅱ类场地第一、二、三组并调幅至PGA为0.2g后作为地震波输入,借助谱分析软件得到延性系数分别为2、3、4、5、6、7、8时的累积延性比谱,如图6所示。对不同地震分组,当结构的阻尼比和后期刚度给定时,延性系数对累积延性比值的影响明显:一方面,随着延性系数的不断增大,累积延性比逐渐增大,主要原因考虑为延性系数体现结构塑性变形的能力,该系数越大,则意味着结构在强震中能够消耗的地震能量越多,相应的累积延性比越大;另一方面,当延性系数等量递增变化时,其对应的累积延性比也几近呈等量递增变化。结构延性系数对谱形状影响较小。此外,累积延性比谱值随周期变化上下浮动不大,可认为全长周期内累积延性比数值稳定,即可不考虑周期对延性比谱的影响。

(a)Ⅱ类场地,第一组,ζ=0.05,p=0.05

(b)Ⅱ类场地, 第二组,ζ=0.05,p=0.05

(c)Ⅱ类场地, 第三组,ζ=0.05,p=0.05图6 延性系数对累积延性比谱的影响
1.7 后期刚度的影响
为了考察双线性弹塑性模型中不同后期刚度对累积延性比谱的影响,以阻尼比为0.05,延性系数μ分别为2、4、6的弹塑性SDOF体系为研究对象,以Ⅱ类场地第一组并将PGA调幅至0.2g后作为地震波输入,借助谱分析软件,经数据处理得到模型不同后期刚度时的累积延性比谱,如图7所示。由图7可知,随着后期刚度的不断增大,累积延性比随之变化。其中当周期相同后期刚度分别为0.02、0.05、0.10、0.20时,累积延性比逐渐增加,且增幅随着周期的不断增大有减小趋势。当后期刚度由0.20增大到0.50时,累积延性比数值变小。同时,累积延性比数值随周期增大呈减小趋势。

(a)Ⅱ类场地,第一组,ζ=0.05,μ=2

(b)Ⅱ类场地,第一组,ζ=0.05,μ=4

(c)Ⅱ类场地,第一组,ζ=0.05,μ=6图7 后期刚度对累积延性比谱的影响
2 累积延性比谱的建立
根据各参数对累积延性比谱的影响规律,参考文献[21],根据原始数据呈现的散点图统计规律,确定累积延性比谱的数学模型为式(4)。
RH=q1q2f(T,ζ,μ,p)=q1q2f(ζ)f(p)f(μ)
(4)
式中:q1、q2分别为考虑场地类别影响和设计地震分组影响的参数;参数ζ、p、μ依次为阻尼比、后期刚度、延性系数;f(ζ)、f(p)、f(μ)分别为一次函数、二次函数、二次函数。经分析,地震波幅值对累积延性比谱没有影响,结构周期对累积延性比谱影响较小,均可忽略不计,故最终数学模型式(4)中参数不含地震波幅值及结构周期。
2.1 模型参数拟合方法
由于Ⅱ类场地地震波样本空间较大,故本节分析时主要以Ⅱ类场地对应的累积延性比谱为基准,其他Ⅰ、Ⅲ、Ⅳ类场地谱值主要用于验证累积延性比谱表达式的合理性。
1)采用Ⅱ类场地所有记录计算弹塑性SDOF体系对应不同阻尼比的累积延性比谱;
2)首先计算给定阻尼比及后期刚度但延性系数不同时的弹塑性SDOF体系的累积延性比谱,接着计算给定阻尼比及延性系数但后期刚度不同时的弹塑性SDOF体系的累积延性比谱;
3)对不同的延性系数,按照式(3)利用最小二乘法进行拟合,从而得到二次函数f(μ)中的各系数(常数);
4)当阻尼比、后期刚度改变时重复步骤3可分别得到一次函数f(ζ)、二次函数f(p)中的各系数(常数);
5)经前文分析知,在周期全长范围内,累积延性比谱值基本稳定,故可利用不同场地下的累积延性比谱值的平均值考虑场地类别影响,从而确定系数q1。同理,可得系数q2。
2.2 模型参数的确定
基于前文选取的地震波的弹塑性时程分析,通过变化结构周期T(0.05~6.00 s)、阻尼比ζ(ζ为0.01、0.02、0.035、0.05、0.10、0.20)、延性系数μ(μ为2、3、4、5、6、7、8)和后期刚度p(p为0、0.02、0.05、0.10、0.20、0.50),提取弹塑性SDOF体系输入每组地震波后进行时程分析所得累积延性比的平均值,拟合出累积延性比谱的数学表达式(5)~(8),分析得到的结果也表明地震波幅值对弹塑性SDOF体系的累积延性比没有影响,结构周期影响较小,均可忽略不计。
RH=q1q2f(T,ζ,μ,p)=q1q2f(ζ)f(p)f(μ)
(5)
f(ζ)=0.52ζ+0.75
(6)
f(p)=-6.2p2+4.0p+0.856
(7)
f(μ)=1.63μ3+0.75μ-2.38
(8)
式中:q1为场地类别影响系数,当为Ⅰ0、Ⅰ1、Ⅱ、Ⅲ、Ⅳ类场地时,q1分别取1.1、1.1、1.0、1.2、1.3;q2为设计地震分组影响系数,当设计地震分组为第一、二、三组时,q2分别取1.0、1.1、1.0。
图8~10分别为改变阻尼比、延性系数、后期刚度时Ⅱ类场地不同设计地震分组累积延性比谱与拟合谱的对比。由图可知,不同设计地震分组时累积延性比谱的形状变化较大,设计地震分组为第一组时地震波高频成分偏多,周期较小时累积延性比较大,设计地震分组为第三组时地震波低频成分偏多,多发生累积损伤,累积延性比较稳定。其中图10显示:当p为0.2和0.5时,累积延性比的相应拟合值与分析值相差较大且偏于保守,主要因为累积延性比可视为结构累积的塑性侧移与屈服侧移之比,反映了地震激励下结构累积损伤的程度;后期刚度系数反映了结构的屈服后行为,后期刚度越大,结构的屈服后行为越接近弹性,因此后期刚度为0.02时拟合精度最高。由图8~10可知,本文提出的模型能较好地对累积延性比谱进行估计,具有合理性。

(a)第一组

(b)第二组

(c)第三组图8 不同阻尼比下Ⅱ类场地累积延性比谱的比较(μ=4,p=0)

(a)第一组

(b)第二组

(c)第三组图9 不同延性系数下Ⅱ类场地累积延性比谱的比较(ζ=0.05,p=0.05)

(a)第一组
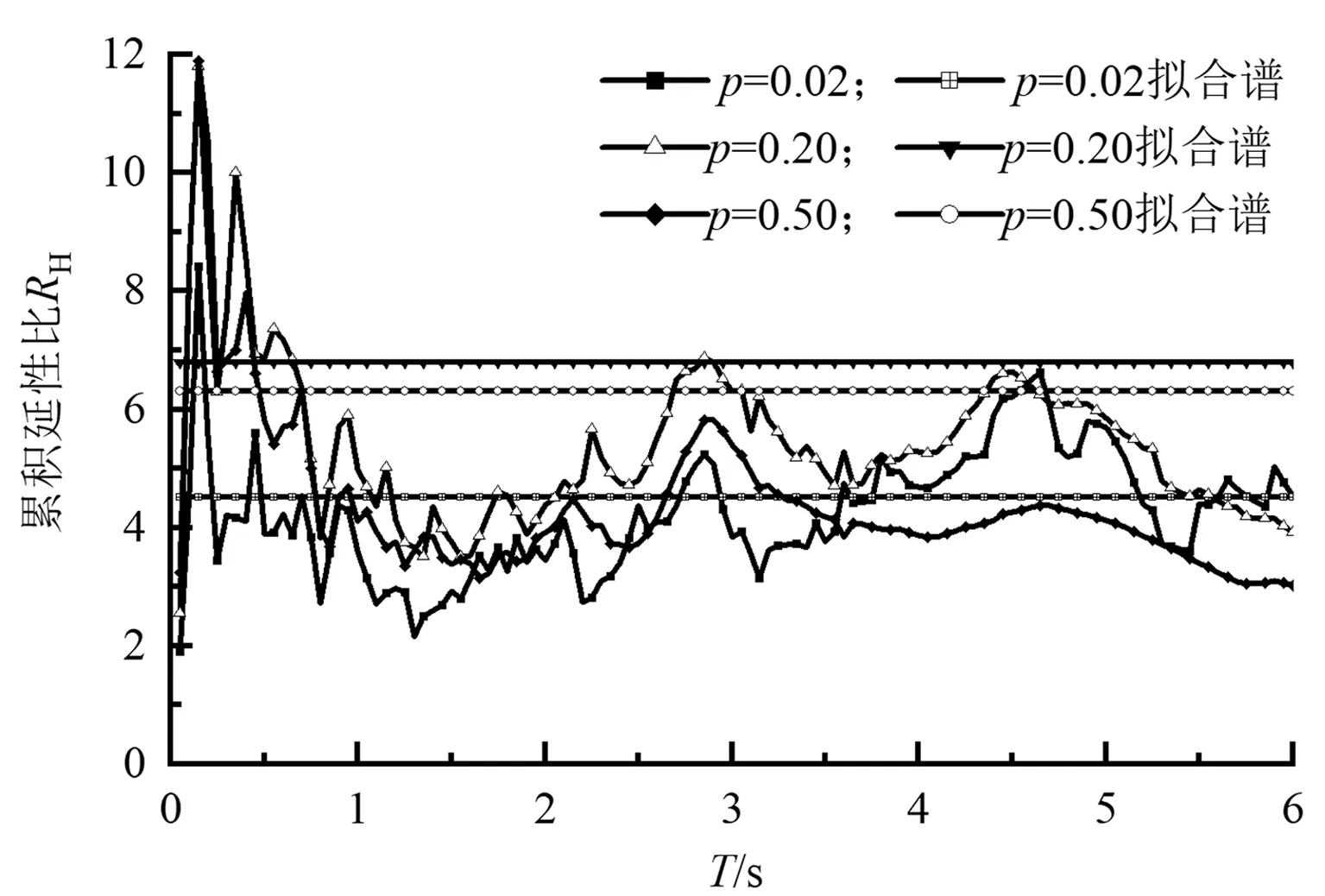
(b)第二组
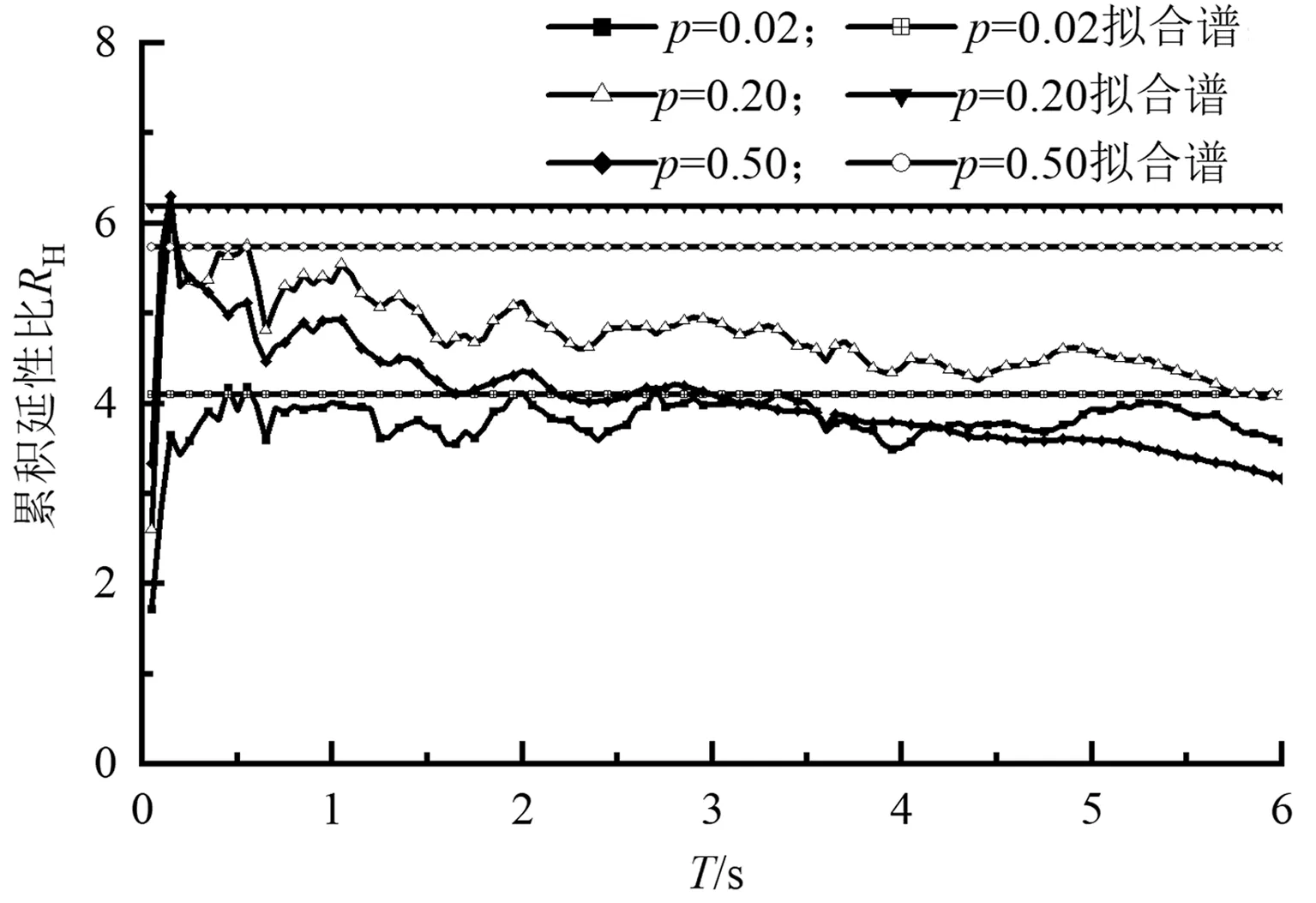
(c)第三组图10 不同后期刚度下Ⅱ类场地累积延性比谱的比较(ζ=0.05,μ=2)
3 结语
本文的主要工作是建立了基于能量性态设计所需的累积延性比谱。为与我国现行抗震规范接轨,采用已明确场地类别的750条天然地震记录,并在每一类场地中按特征周期指标进行设计地震分组,将15组地震记录输入谱分析软件中进行弹塑性时程分析,从而得到了地震波幅值、结构周期、阻尼比、延性系数、后期刚度、场地类别、设计地震分组等因素对累积延性比谱的影响规律。分析表明:累积延性比谱形状、大小均与地震波幅值无关,与结构周期关系不大,可以忽略;当阻尼比和延性系数分别增大时,累积延性比呈增大趋势,另外,后期刚度、场地类别、设计地震分组对累积延性比谱均有不同程度的影响。分析各因素的影响规律后建立了符合中国场地分类的累积延性比谱,明确了结构累积滞回耗能需求与结构单向推覆耗能之间的关系。

