基于随机有限断层方法的唐山地震强地面运动模拟
兰景岩 王延伟 刘娟 齐文浩
摘要:基于动力学拐角频率的随机有限断层模型,以1976年唐山大地震的极震区为研究目标,通过梳理前人的研究成果,建立了目标区的计算模型并确定了震源模型参数,依靠目标区的局部场地资料和场地动力学参数,利用四分之一波长法,获取局部场地放大效应参数;利用随机有限断层模型地震动模拟方法,给出了唐山大地震近场强地震动场模拟结果,并与历史地震宏观烈度进行对比,结果表明:在Ⅷ、Ⅸ度影响烈度的范围与宏观资料吻合较好。
关键词:唐山地震;强地面运动;随机有限断层模型
中图分类号:P315.913 文献标志码:A 文章编号:1000-0666(2019)04-0503-07
0 引言
由地震引发的强地面运动是造成工程结构破坏和地表地质灾害的主要触发因素,强地震动的发生、传播和运动学特性是工程地震学的主要研究内容。科学合理地预测、估计和模拟强地面运动是有效减轻地震灾害损失的重要途径和手段。
强震动观测记录是工程抗震设防依据和工程地震学研究的重要基础数据,对于缺乏强震记录地区,用定量化的表现形式来模拟强地面运动基本参数(幅值、频谱、持时)是非常重要的研究内容。目前,关于强地面运动模拟方法归纳起来有3种:确定性方法(Aki,1968;Hartzell,1978;Irikura,1983)、随机方法(Beresnev,Atkinson,1998;Boore,2003;Zeng et al,1994;Irikura,1983)以及混合方法。相比较而言,基于随机方法的有限断层模型因能够较好地反映短周期地震动的随机性,模拟近场和大震高频成分地震动效果较好,并且能够模拟区域地震动场形成理论地震图或烈度图,近十几年来利用有限断层模型开展地震动场模拟和预测,已在大多数城市活动层断层技术工作中得到了积极的推广(陶夏新,王国新,2003;王国新,史家平,2008;刘海明等,2010;盛俭等,2012;申文豪等,2013;张冬峰等,2018),并取得了一系列丰富的成果。
针对近些年的几次强震,例如美国加州Landers7.3级地震(Pacor et al,2005)、汶川8.0级地震(王卫民等,2008;王国新,史家平,2009;常莹等,2012)、玉树7.1级地震(王海云,2010)、美国西部Northridge6.7级地震(张翠然等,2011)、卢龙5.7级地震(李启成等,2012)、芦山7.0地震(孙晓丹等,2013)、鲁甸6.5级地震(王振宇,2017;魏勇等,2018),通过对比近场强震动实测记录,均能够较好地验证随机有限断层模型方法在近场强震动模拟中的适用性和可行性。1976年发生的唐山7.8级大地震,至今已过去40多年,限于当时强震动观测手段和记录的缺失,无法利用近场强震记录对现阶段的地震动模拟结果进行有效检验,尽管如此,关于唐山大地震近断层强地面运动研究也未曾停止,至今已积累了比较丰富的研究成果。Dan等(1993)利用唐山第二大余震MS6.9的实测记录,采用经验格林函数方法,模拟了唐山主震和几个余震的强震区近场加速度时程及特征谱。谢礼立等(1994)建立了非均匀的唐山主震断层模型,利用广义反射-透射系数矩阵和离散波数法,给出了唐山及周边地区地震动时程的数值模拟结果。罗奇峰和胡聿贤(1997)通过建立非均匀的唐山地震断层模型,基于改进的经验格林函数法,利用唐山余震记录模拟了唐山主震近场及远场台的加速度时程。蔡永恩等(1999)利用LDDA方法,模拟了唐山地震断层的破裂、错动和应力释放的整个动力过程。Robinson和Zhou(2005)研究了唐山地震主震和余震之间的静态应力相互作用。杜晨晓等(2010)利用三维有限差分断层瞬态破裂动力学模型,对唐山地震发震断层的动态破裂及近断层地表运动特征进行了仿真模拟和计算。刘启方和李雪强(2011)基于显式并行有限元方法,利用有限移动源模型和随机地震动合成方法模拟了高频地震动,利用宽频带地震动模拟技术,估计了唐山近场地震动分布,给出了极震区加速度时程和反应谱。
在总结前人研究的基础上,本文基于强震近场地震动特征,将1976年7月28日唐山大地震极震区作为研究区,考虑到强震近场特征及近断层效应,利用Motazedian和Atkinson(2005)基于随机有限断层方法合成地震动的Exsim-Beta程序,给出唐山大地震近场强地面运动模拟结果,并与实际的宏观烈度进行对比,印证该方法的可靠性和适用性。
1 随机有限断层模型方法
随机有限断层模型方法的基本思路是将地震断层面视为由若干个(NL×NW)个子断层的集合,每个子断层即为一个点源(或子源)。地震的破裂过程是从破裂起始点以一定的破裂速度(一般为剪切波速的0.8倍)向外呈辐射状传播,当传播到每个子源的中心时,该子源被触发,每个子断层在观测点产生的加速度时程由随机点源模型计算得到,整个断层在观测点所产生的加速度时程a(t)是在考虑子断层合理的时间延滞的基础上叠加得到的:
式中:NL,NW分别为沿着断层走向和倾向划分的子断层数;Δtij为地震波从破裂起始点传播至第ij个子源的时间延迟与该子源至观测点的传播时间延迟之和;aij(t)为第ij个子源在观测点由剪切波引起的地震动。
根据Motazedian和Atkinson(2005)的动力学拐角频率来描述震源谱的模型,将第ij个子源的震源加速度谱定义为:
式中:M0為地震矩(单位:dyne-cm);C为比例系数;Hij是保证子源高频辐射守恒的标度因子,是包含品质因子Q,κ因数等参数的函数形式(Atkinson,Boore,1995)。f0为拐角频率,定义为:
式中:Δσ为应力降(单位:bar);β为震源附近剪切波速度(单位:km/s)。
2 模型的建立和计算参数的确定
2.1 目标区震源模型参数的确定
本文以1976年唐山地震为例,建立随机有限断层震源模型,并确定该模型的相关参数。根据国家地震局(1982)提供的发震构造分析和震源机制结果,唐山地震是一个近乎走滑型地震,发生在唐山菱形块体内的唐山断裂带上。张之立等(1989)按照重新定位后的震源位置及更多的补充资料,重新计算出可能破裂长度为77 km,这与陈运泰等(1979)用地形变反演得到的结果(84 km)基本一致。考虑到这些结果,本文选取的唐山地震的平面几何模型如图1所示。参考Beresnev和Atkinson(2002)提出的子断层划分依据和原则,结合杜晨晓(2010)年给出唐山主震的断层面位移滑动分布,绘制了唐山地震的子断层及滑动模型图(图2)。
研究区域(39°~40°N,117°~119°E)网格精度为0.03°(~3 km),共计1 984个网格点。计算每个网格点的峰值加速度(PGA)、峰值速度(PGV)、峰值位移(PGD)以及网格点到断层的最短距离D。综上所述,用于模拟1976年唐山地震的模型参数如表1所示。
2.2 目标区场地放大效应
用于评价场地放大效应的方法主要有标准谱比法、地脉动法和波阻抗法。对于特定的场地,只有弄清场地土层分布和波速结构等,才能合理估算场地对基岩地震动的影响。标准谱比法需要一个处在稳定基岩的台站作为参考台,且假设2个台站接收到的地震波是一致的,并忽略地震波在2个观测台站之间的衰减作用。地脉动法是基于单台的谱比法,由于其简单便捷而受到工程界的广泛应用,但是其重要假设基岩处的HVSR谱比值为1,在有些的研究中,这种假设尚值得商榷。波阻抗法又称四分之一波长法(Boore,2013),依靠研究区的局部场地资料和场地动力学参数,经过统计分析给出的,适合于工程地质资料、剪切波速资料丰富的地区,且浅部的场地模型能够更加真实地反映场地的放大效应。
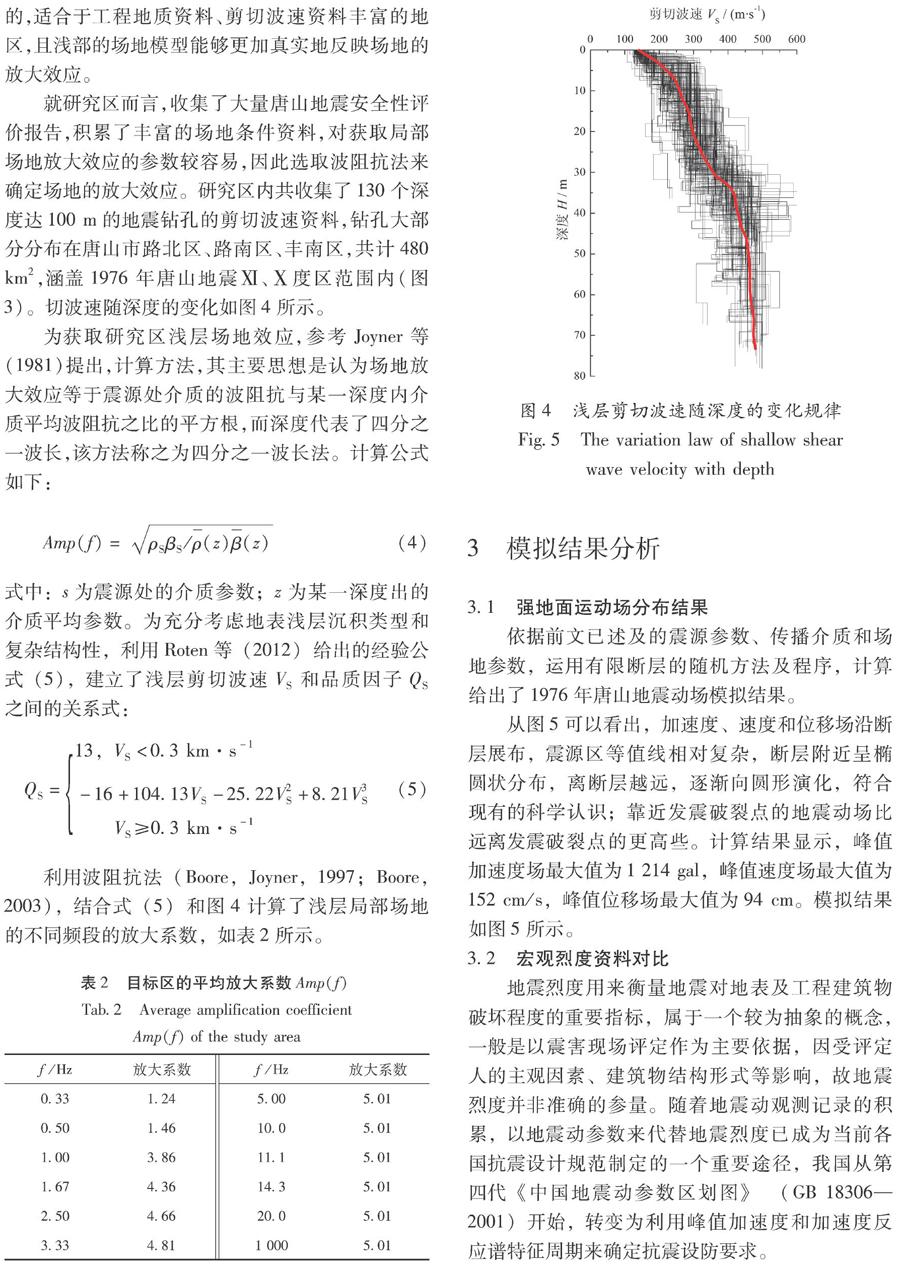
就研究区而言,收集了大量唐山地震安全性评价报告,积累了丰富的场地条件资料,对获取局部场地放大效应的参数较容易,因此选取波阻抗法来确定场地的放大效应。研究区内共收集了130个深度达100 m的地震钻孔的剪切波速资料,钻孔大部分分布在唐山市路北区、路南区、丰南区,共计480 km2,涵盖1976年唐山地震Ⅺ、Ⅹ度区范围内(图3)。切波速随深度的变化如图4所示。
为获取研究区浅层场地效应,参考Joyner等(1981)提出,计算方法,其主要思想是认为场地放大效应等于震源处介质的波阻抗与某一深度内介质平均波阻抗之比的平方根,而深度代表了四分之一波长,该方法称之为四分之一波长法。计算公式如下:
式中:s为震源处的介质参数;z为某一深度出的介质平均参数。为充分考虑地表浅层沉积类型和复杂结构性,利用Roten等(2012)给出的经验公式(5),建立了浅层剪切波速VS和品质因子QS之间的关系式:
利用波阻抗法(Boore,Joyner,1997;Boore,2003),结合式(5)和图4计算了浅层局部场地的不同频段的放大系数,如表2所示。
3 模拟结果分析
3.1 强地面运动场分布结果
依据前文已述及的震源参数、传播介质和场地参数,运用有限断层的随机方法及程序,计算给出了1976年唐山地震动场模拟结果。
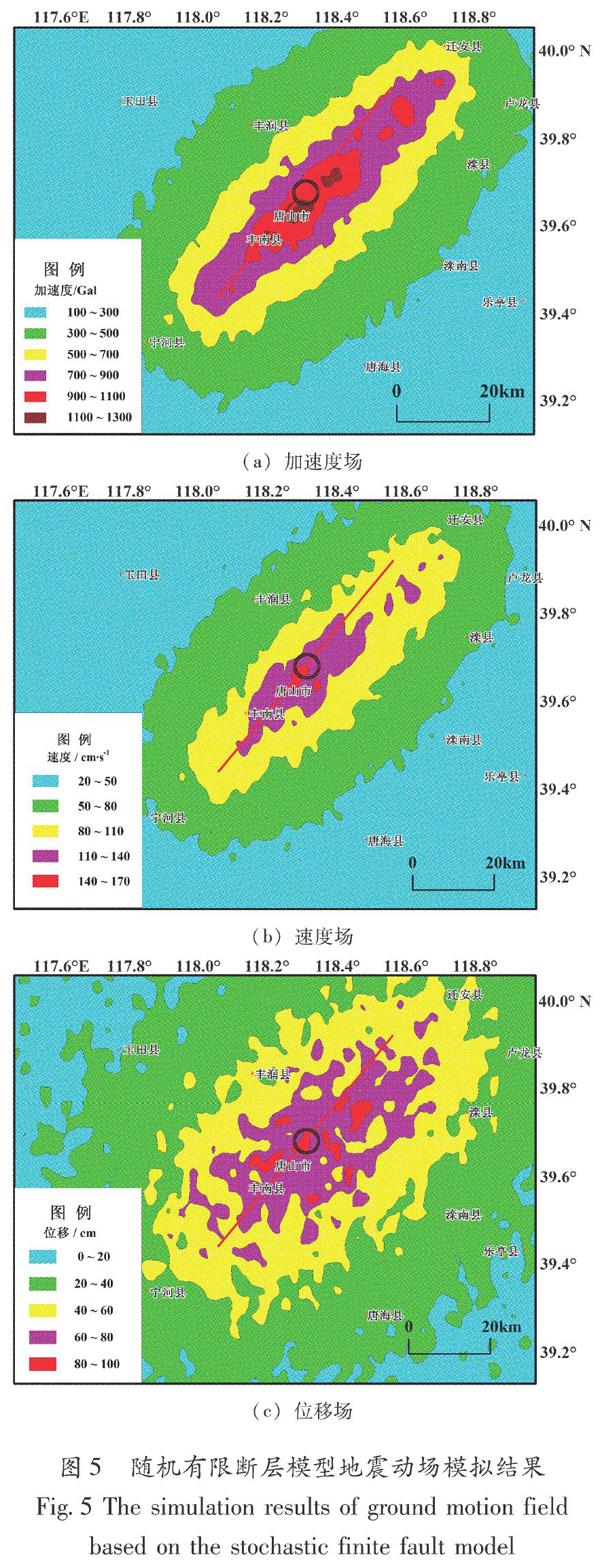
从图5可以看出,加速度、速度和位移场沿断层展布,震源区等值线相对复杂,断层附近呈椭圆状分布,离断层越远,逐渐向圆形演化,符合现有的科学认识;靠近发震破裂点的地震动场比远离发震破裂点的更高些。计算结果显示,峰值加速度场最大值为1 214 gal,峰值速度场最大值为152 cm/s,峰值位移场最大值为94 cm。模拟结果如图5所示。
3.2 宏观烈度资料对比
地震烈度用来衡量地震对地表及工程建筑物破坏程度的重要指标,属于一个较为抽象的概念,一般是以震害现场评定作为主要依据,因受评定人的主观因素、建筑物结构形式等影响,故地震烈度并非准确的参量。随着地震动观测记录的积累,以地震动参数来代替地震烈度已成为当前各国抗震设计规范制定的一个重要途径,我国从第四代《中国地震动参数区划图》(GB 18306—2001)开始,转变为利用峰值加速度和加速度反应谱特征周期来确定抗震设防要求。
(a)加速度场
(b)速度场
(c)位移场图5 随机有限断层模型地震动场模拟结果
在我国现行抗震设计规范中,峰值加速度和地震烈度之间存在一定的转换关系,有研究表明,单一的使用某一种地震动参数转化烈度存在一定的不合理性,主要原因在于地震烈度与峰值加速度(PGA)、峰值速度(PGV)有高度相关性,峰值加速度(PGA)随距离衰减较快,能够反应近场烈度分布,而峰值速度(PGV)随距离衰减较慢能够反应远场烈度分布(申文豪等,2013)。美国地质调查局的研究人员利用美国加州地震数据,给出了不同类型地震动参数与修正麦卡利烈度(简称:MMI)的经验关系,并指出结合2种地震动参数得到的MMI比单一地震动参数得到的MMI的标准偏差要小(Worden et al,2012)。
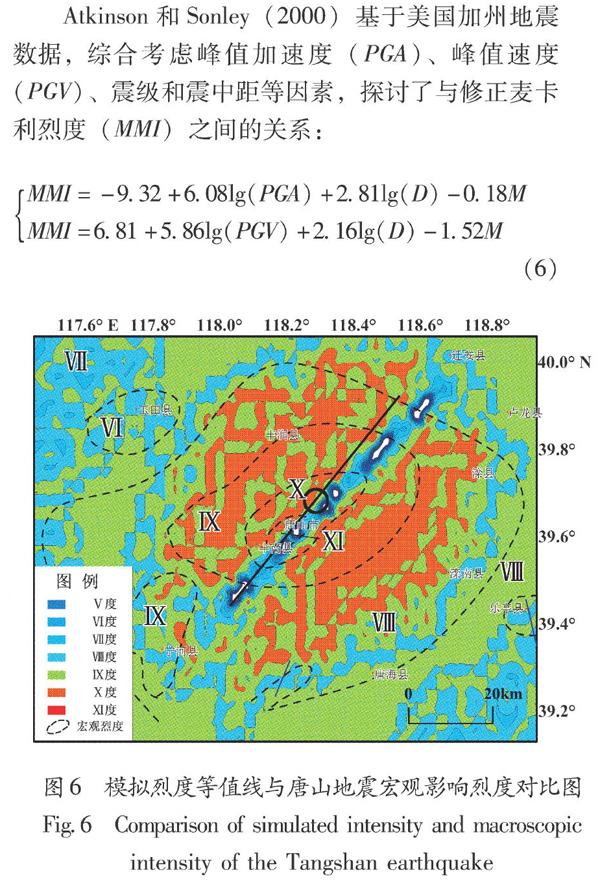
Atkinson和Sonley(2000)基于美国加州地震數据,综合考虑峰值加速度(PGA)、峰值速度(PGV)、震级和震中距等因素,探讨了与修正麦卡利烈度(MMI)之间的关系:
MMI=-9.32+6.08lg(PGA)+2.81lg(D)-0.18M
MMI=6.81+5.86lg(PGV)+2.16lg(D)-1.52M(6)
鉴于MMI与《中国地震烈度表》(GB/T 17742—2008)中规定的烈度定义和分级较为接近,利用式(6),计算了研究区的MMI,将结果与1976年唐山地震宏观烈度调查得到的等震线进行对比(图6),可以看出,随机模拟结果在Ⅷ、Ⅸ度影响烈度的范围与宏观资料吻合较好,但由于受到式(6)本身的限制,断层附近区域的烈度要远小于宏观资料的极震区范围。另外,式(6)是基于美国加州地震数据给出的经验公式,由于
各个地方地质构造和场地衰减特征不同,转换公式的系数也会有所差异,在实际应用中结果与实际情况也会存在一定差异。对于加速度、速度以及位移的随机模拟不可避免地存在结果上的不确定,由于唐山主震记录的缺失,使得这种不确定性难以较正,进而会间接影响MMI计算结果的偏差,故模拟烈度与宏观烈度在一定范围内存在着差异和区别也是较符合客观实际的。
4 结论
在充分利用唐山地震钻孔资料、工程地质资料、地震活动性、活断层探测和地震危险性评价的研究成果的基础上,结合前人的工作成果,确定了区域地震应力降、地壳衰减参数(品质因子、交叠距离)和场地高频衰减因子等计算参数,基于震源运动学模型,确定所有的震源全局参数和局部参数,应用随机有限断层模型方法计算给出了目标区活动断层(唐山—古冶断裂)的强地面运动预测结果,主要结论如下:
(1)收集研究区内130个钻孔剪切波速资料,建立了浅层剪切波速VS和品质因子QS之间的关系式,利用波阻抗法确定了研究区的浅层放大系数。
(2)依据所确定的震源参数、传播介质和场地参数,运用有限断层的随机方法及程序,给出了唐山断裂所产生的地震动加速度场、速度场以及位移场,其结果的分布與发震构造唐山—古冶断裂的展布方向一致。
(3)利用地震动参数与烈度之间的转换关系,计算了模拟烈度等值线结果,并与宏观震害影响烈度进行了对比,验证了随机有限断层模型方法在高频地震动模拟方面的可行性和适用性。
(4)第五代《中国地震动参数区划图》(GB 18306—2015)虽然已将唐山极震区的基本设防烈度从过去的0.20 g提升至0.30 g,但限于概率性地震危险性方法本身的原因,无法充分考虑近断层对工程场地的重要影响,因此本文利用随机有限断层方法开展的地震动场模拟结果,对于现阶段高烈度和近断层地区的工程抗震研究工作是十分重要的补充内容,同时对于唐山极震区开展重大工程建设和制定城市防震减灾规划工作,具有一定的工程意义和参考价值。
参考文献:
蔡永恩,何涛,王仁.1999.1976年唐山地震震源动力过程的数值模拟[J].地震学报,21(5):469-477.
常莹,周红,俞言祥.2012.汶川地震强地面运动模拟[J].地震学报,34(2):224-234.
陈运泰,林邦慧,王新华,等.1979.用大地测量资料反演的1976唐山地震的位错模式[J].地球物理学报,22(3):201-217.
杜晨晓,谢富仁,张扬,等.2010.1976年MS7.8唐山地震断层动态破裂及近断层强地面运动特质[J].地球物理学报,53(2):290-304..
国家地震局.1982.一九七六唐山地震[M].北京:地震出版社,31-130.
郭慧,江娃利,谢新生.2011.对1976年河北唐山MS7.8地震地表破裂带展布及位移特征的新认识[J].地震地质,33(3):506-524.
黄聪.2013.基于PGA的地震紧急处置有效预警时间研究[D].哈尔滨:中国地震局工程力学研究所.
拉巴次仁.2013.随机有限断层方法模拟地震动[J].华中师范大学学报(自然科学版),47(4):583-586.
李启成,池红岩,宋志勇.2012.卢龙地震动场的预测[J].地震研究,35(2):240-245.
刘海明,陶夏新,孙晓丹,等.2010.马衔山北缘断裂西段地震动场估计的震源模型[J].世界地震工程,26(3):60-66.
刘启方,李雪强.2011.唐山大地震近场宽频带地震动模拟[J].地震工程与工程振动,31(5):1-7.
罗奇峰,胡聿贤.1997.1976年唐山地震近、远场加速度的半经验合成[J].地震学报,19(3):275-282.
申文豪,仲秋,刘博研,等.2013.基于改进的随机有限断层模型进行区域烈度速报[J].地球物理学进展,28(2):695-705.
盛俭,薄景山,佴磊,等.2012.近断层地震动场预测——以长春市为例[J].地震工程与工程振动,32(2):48-53.
孙晓丹,王罡,刘成清.2013.芦山地震有限断层混合震源模型模拟[J].地震工程与工程振动,33(4):15-20.
陶夏新,王国新.2003.近场强地震动模拟中对破裂的方向性效应和上盘效应的表达[J].地震学报,25(2):191-198.
王国新,史家平.2008.近场强地震动合成方法研究及地震动模拟[J].东北地震研究,24(2):4-10.
王国新,史家平.2009.随机有限断层法在汶川强地震动模拟中的应用[J].自然科学进展,19(6):664-669.
王海云.2010.2010年4月14日玉树MS7.1地震加速度场预测[J].地球物理学报,53(10):2345~2354.
王卫民,赵连峰,李娟,等.2008.四川汶川8.0级地震震源过程[J].地球物理学报,51(5):1403-1410.
王振宇.2017.高频地震动随机模拟方法研究[D].哈尔滨:中国地震局工程力学研究所.
魏勇,崔建文,王秋良,等.2018.基于合成地震動的2014年鲁甸MS6.5地震场地效应分析[J].地震研究,41(1):32-37.
谢礼立,张敏政,曲传军.1994.唐山主震近场地震动的模拟[J].地震工程与工程振动,14(3):1-10.
张翠然,陈厚群,李敏.2011.采用随机有限断层法生成最大可信地震[J].水利学报,42(6):721-728.
张冬峰,付长华,吕红山,等.2018.随机有限断层法及其工程应用中的问题分析[J].震灾防御技术,13(4):784-800.
张之立,王成宝,方兴,等.1989.唐山地震破裂过程的雁行断裂模式及理论和试验的模拟[J].地震学报,11(3):291-302.
赵翠萍,陈章立,华卫,等.2011.中国大陆主要地震活动区中小地震震源参数研究[J].地球物理学报,54(6):1478-1489.
Aki K.1968.Seismic displacements near a fault[J].Journal of Geophysical Research,73(16):5359-5376.
Atkinson G M,Boore D M.1995.Ground-motion relations for Eastern North America[J].Bulletin of the Seismological Society of America,85(1):17-30.
Atkinson G M,Sonley E.2000.Empirical relationships between modified Mercalli intensity and response spectra[J].Bulletin of the Seismological Society of America,90(2):537-544.
Beresnev I A,Atkinson G M.1997.Modeling finite-fault radiation from the ωn spectrum[J].Bulletin of the Seismological Society of America,87(1):67-84.
Beresnev I A,Atkinson G M.1998.FINSIM--A Fortran Program for Simulating Stochastic Acceleration Time Histories from Finite Faults[J].Seismological Research Letters,69(1):27-32.
Beresnev I A,Atkinson G M.2002.Source parameters of earthquakes in eastern and western North America based on finite-fault modeling[J].Bulletin of the Seismological Society of America,92(2):695-710.
Boore D M,Joyner W B.1997.Site amplifications for generic rock sites[J].Bulletin of Seismological Society of America,87(2):327-341.
Boore D M.2003.Simulation of ground motion using the stochastic method[J].Pure and Applied Geophysics,160(3):635-676.
Boore D M.2013.The uses and limitations of the square-root-impedance method for computing site amplification[J].Bulletin of the Seismological Society of America,103(4):2356-2368.
Dan K,Ishii T,Ebihara M.1993.Estimation of strong ground motions in meizoseismal region of the 1976 Tangshan,China,Earthquake[J].Bulletin of the Seismological Society of America,83(6):1756-1777.
Hartzell S.1978.Earthquake aftershock as Greens function[J].Geophysical Research Letters,5(1):1-4.
Irikura K.1983.Semi-empirical estimation of strong ground motions during large earthquake[J].Bull Disas Prev Res Inst,Kyoto Univ.,35(2):63-104.
Joyner W B,Warrick R E,Fumal T E.1981.The effect of quaternary alluvium on strong ground motion in the Coyote Lake,California,Earthquake of 1979[J].Bulletin of the Seismological Society of America,71(4):1333-1349.
Motazedian D,Atkinson G M.2005.Stochastic finite-fault modeling based on a dynamic corner frequency[J].Bulletin of the Seismological Society of America,95(3):995-1010.
Pacor F,Cultrera G,Mendez A et al.2005.Finite fault modeling of strong ground motions using a hybrid deterministic-stochastic approach[J].Bulletin of the Seismological Society of America,95(1):225-240.
Robinson R,Zhou S.2005.Stress interactions within the Tangshan,China,Earthquake Sequence[J].Bulletin of the Seismological Society of America,95(6):2501-2505.
Roten D,Olsen K,Pechmann J.2012.3D simulations of M7 earthquakes on the Wasatch Fault,Utah,part II:broadband(0-10Hz)ground motions and nonlinear soil behavior[J].Bulletin of the Seismological Society of America,102(5):2008-2030.
Worden C B,Gerstenberger M C,Rhoades D A,et al.2012.Probabilistic relationships between ground-motion parameters and modified Mercalli intensity in California[J].Bulletin of the Seismological Society of America,102(1):204-221.
Zeng Y,Anderson J G,Yu G.1994.A composite source model for computing realistic synthetic strong ground motions[J].Geophysical Research Letters,21(8):725-728.
GB/T 17742—2008中國地震烈度表[S].
Strong Ground Motion Simulation of the Tangshan EarthquakeBased on the Stochastic Finite Fault Method
LAN Jingyan1,2,WANG Yanwei1,2,LIU Juan2,3,QI Wenhao3
(1.Beijing university of technology,Beijing 100022,China)(2.Guilin University of technology,Guilin 541004,Guangxi,China)(3.Institute of Engineering Mechanics,China Earthquake Administration,Harbin 150080,Heilongjiang,China)
Abstract
Based on the stochastic finite fault model of the dynamic corner frequency,we take the meizoseismal area of the Tangshan earthquake in 1976 as the research goal.The calculation model of the target zone is established and the parameters of the source model are determined by summarizing the research results of predecessors.The local site amplification is obtained by using the quarter-wavelength method based on the site condition data and soil dynamics parameters.The simulation results of the near-field strong ground motion field of the Tangshan earthquake are obtained by using the stochastic finite fault model ground motion simulation method.The results show that the ranges of VIII,IX degree simulated are similar to macro intensity comparing with the macroscopic intensity of historical earthquakes.
Keywords:the Tangshan earthquake;strong ground motion;stochastic finite fault model

