复连续小波变换实现地震波在任意时-频域随机相位的方法
谢皓宇 本田利器 郑万山

摘要:动力分析过程中输入地震波的选择非常重要,通过扰动自然波生成人工地震波是丰富设计地震波池的方法之一。提出使用复连续小波变换来修改、扰动自然波的方法来拟合人工地震波,以2000年日本鸟取MW6.7地震为研究对象,对比Shannon小波基和Gabor小波基在生成人工波过程中的特点。结果表明:使用改进方法可以在任意指定的时-频域上修改地震波的相位谱从而产生人工波,且Shannon小波对地震波能量的保留优于Gabor小波,故 Shannon小波基是更好的选择。
关键词:抗震设计;人工地震波;小波变换;地震动输入
中图分类号:P315.91 文献标志码:A 文章编号:1000-0666(2019)04-0510-06
0 引言
随着基于性能的抗震设计(Deierlein et al,2003;吕大刚等,2006)理念的出现和发展,时程动力分析成为了现代抗震设计中的一个重要方法。近年来,越来越多的普通学者和设计人员也能够利用具备足够能力的计算机进行复杂的数值分析,而在抗震设计领域时程动力分析的过程中,设计输入地震波的选择尤为重要。
传统上设计输入地震波的选择方法通常包括:通过设计反应谱拟合出人工地震波(胡聿贤,何训,1986;张郁山,赵凤新,2014);通过断层物理模型模拟人工地震波(Koller et al,1996;Kamae,Irikura,1998;Hata et al,2011);直接使用历史记录的自然地震波,通过修改扰动自然地震波生成人工地震波。3种方法各有优缺点,通过设计反应谱拟合人工地震波方法使用反应谱与功率谱密度之间的近似数学关系,将得到的功率谱密度转化成傅里叶幅值谱之后进行多次迭代,最终得到人工地震波,这个方法快速、经济,但反应谱和功率谱密度之间的数学关系还无法准确地模拟,使得反应谱拟合精度有限,另外靠此法生成的人工波在波形和频谱上仍和自然波存在较大差异。通过断层物理模型模拟人工波,比如经典格林方程的方法,它的缺点是于对长周期部分模拟精度较低。直接使用目标场地附近历史记录的自然波作为设计输入需要面对自然波记录的数量有限的问题。通过信号处理的手段随机修改扰动自然地震波生成人工地震波的方法能保留自然波的大部分特性,同时丰富了设计地震波池,综合来说是更先进的方法。
除上述3种方法外,还有一种随机方法(Boore,2003),通过傅里叶变换将自然波信号分解成傅里叶系数,即幅值谱与相位谱,在保留幅值谱的情况下扰动相位谱之后逆变换形成人工新波。
该方法利用基底的时移不变性以及正交性,使得产生的新波在总能量上不会有太大波动,同时逆变换的新波具有唯一性。但随机方法仍有2个问题,首先eift作为基底使得扰动在会在时域的-∞到+∞分布,因此扰动无法人为任意地落在特定局部的时域上,其次人工波在时域上的能量分布也会较原始波发生明显的变化,原始波时域上能量集中的部分将会在人工波中分散。
小波变换作为与傅里叶变换类似的信号处理方法,和傅里叶变换不同的是可以同时解析出信号在时域和频域的成分。基于这个特点,本文采用小波变换作为扰动自然波生成人工波的工具,提出一种新的计算方法,实现连续小波对地震波信号处理的逆变换。
1 复小波变换的相位谱
传统的利用傅里叶变换扰动自然波的随机方法过程如下所示。
分解原始波并体换相位谱:
通过傅里叶逆变换重构地震波:
式中:Δt为原始信号的采样间隔;Δf为频谱的采样间隔;σ(fk)则是人为修改傅里叶相位谱的扰动谱。可以看到,随机方法中使用eift作为基底对于扰动时空控制仅处在频域而不在时域。
小波变换利用脉冲母小波ψ(s,τ)对信号波的卷积,将信号分解为时移成分(τ)和尺度成分(s),分别描述了信号波在时域和频域的分布情况。针对使用小波变换来随机修改自然波,需要解决小波变换没有明晰的相位谱的问题。
Honda等最早提出使用复离散解析小波变换来分析信号波(Honda,Ahmed,2011;Honda,Khatri,2012),解析小波母波本身具有正交性可以使正变换和逆变换保持唯一性,同时解析小波的母波在频域范围内只有正频率的部分,因此可以使原始波与新波在实数范围保持能量不变;而使用复小波生成的小波系数为复数,将复数角定义为相位,类似随机方法。
与式(1)对应,使用复离散解析小波分解原始信号:
并修改相位谱:
与式(2)对应,离散小波逆变换重构成为新的信号(人工波):
式中:W(j,k)为小波系数;ψ(j,k)为母小波;j,k分别代表尺度和时移;过程中小波系数的复数角θ(j,k)与随机方法中的相位角θ(fk)数学形式相似,可以抽象地描述为小波变换后的相位谱。
模拟结果显示,新生成的人工波和原始波之间频域、时域的能量分布在一定分辨率下得到保持,同时总能量基本稳定。但存在使用离散小波仍无法任意指定时-频域的问题,因为离散小波系数的分布是固定的,尺度上分辨率高的部分自然在时移上的分辨率就低。这个问题只能使用连续小波变换来解决。
2 连续小波变换逆变换的方法
和离散小波变换不同,连续小波变换可以在任意的时-频域位置对信号小波系数的相位进行修改。但使用连续小波变换需要解決在有限的计算机运算性能约束下实现小波变换逆变换的问题。按照使用离散小波变换扰动自然波的思路,可以简单地将过程中离散求和的部分替换成积分,但这种方法对计算机的积分精度要求过高,普通工程师和设计人员使用的计算机通常难以实现高精度的连续小波的逆变换,而只有高精度的连续小波逆变换才能准确实现人工波的重构。同时,传统的小波变换逆变换要求小波基的正交性,这使得一些性质良好,适合用于扰动自然地震波的小波基无法在研究中得到使用。
于是本文提出改进方法,在不用进行全时-频域积分的条件下利用连续小波实现原始信号在时-频域的扰动修改,过程如下文所示。
首先,使用连续小波变换将离散信号分解到目标的时-频域内:
式中:s,τ分别代表尺度和时移。将原始离散波减去计算出的小波系数,再对小波系数添加扰动相位θ(s,τ)后加上去,并乘以经验系数c控制时-频域的精度:
为了进一步提升本方法的随机程度,尤其是对能量扰动的随机程度,并考虑到复数角的性质,再增加一个扰动相位,此时2个随机扰动相位分别为θ1(s,τ)和θ2(s,τ):
本文分别采用以Shannon小波(Cattani,2008)和Gabor小波(Lee,1996)为母波的复连续小波变换作为研究工具。Shannon小波的定义为:
式中:FB代表小波带宽;FC代表小波的中心频率。使用复Shannon小波的原因是复Shannon小波为解析波,即对实数小波逆变换可以是新波与原始波之间的能量保持一致。同时Shannon小波母波具有正交性,满足逆变换的唯一性。Gabor小波的定义为:
式中:x0代表脉冲中心;a代表指数衰减速率;k0代表控制调幅率。Gabor小波不具备正交性,按照连续小波变换定义中的逆变换本无法对人工波进行重构,但根据本文提出的新的逆变换方法,参考式(10),则可以使用Gabor小波来重构人工波。Gabor小波最大的特点是将时-频域中标准差的内积压缩到了最小,也就是可以将小波变换的分辨率提高,将时-频信息的不确定性压缩到最小。
3 数值模拟
本文将2000年日本鸟取MW6.7地震作为研究对象,震中位于日本鸟取县米子市和松江市之间。鸟取地震是一次典型的发生在城市的强震。
本文使用的地震波数据由日本防灾科学技术研究所强震观测网提供,观测站点号为KYT001,使用FW向成分数据,持时119 s,采样频率100 Hz。经过0.1~10 Hz范围之外的降噪处理以及增幅处理后,波形和对应的傅里叶幅值谱见图1。
由图2可见,Shannon小波与Gabor小波的幅值谱在时域(时移)上与傅里叶谱基本一致,而在频域(尺度)上也有高度类似的形状,区别的原因在于母波的基频不同,因此在频域上2个幅值谱呈倍数关系。根据小波幅值谱的峰值分布特点,本文使用Shannon小波对地震波进行扰动时选择时移为15~45 s,选择尺度为0~3;使用Gabor小波对地震波进行扰动时选择时移为15~45 s,选择尺度为0~0.5。考虑计算机性能的限制,将在设定的区域内取10 000个随机点作为扰动点,再根据式(10)取10 000对随机相位θ1及θ2作为扰动相位,各进行20次扰动模拟。
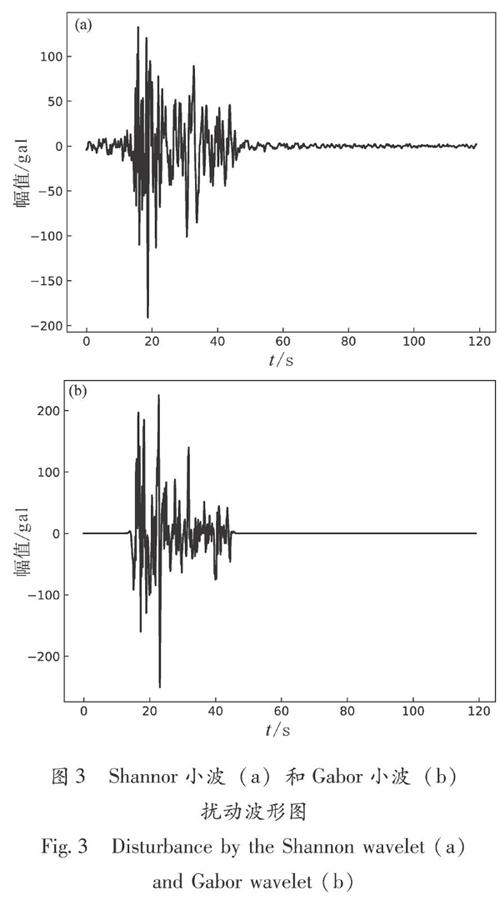
Shannon小波扰动鸟取地震的模拟结果显示,扰动如预期集中在了设定的时域范围内,在地震波的总能量控制上,20次模拟中有10次能量增加以及10次能量减少,变化范围在2%以内。抽取其中一次模拟结果,扰动见图3a。
Gabor小波扰动鸟取地震的模拟结果显示,扰动集中在设定的时域范围内,效果比Shannon波更好。但在地震波的总能量控制上,和Shannon波模拟中取相等的经验系数c时,20次模拟中能量几乎都是增加。抽取其中一次模拟结果,扰动见图3b。
由于Gabor小波基有复数小波基中最小的标准差内积,因此它生成的扰动在非目标时域内的噪音比Shannon小波更小。但Gabor小波基不具备正交性以及对地震波实数部分能量的保留,因此无法做到Shannon小波生成新波对总能量的约束。需要注意的是,本次模拟的经验系数c都取的0.05,在Gabor扰动模拟中调整经验系数的取值获得的能量更接近原始设计波的结果,而本文统一经验系数的取值主要是为了方便对比Shannon小波扰动和Gabor小波扰动的差异。Shannon小波和Gabor小波扰动20次模拟得到的人工地震波能量分布如图4所示。可以看到Shannon小波比Gabor小波相比更能约束人工波的能量变化。从这个角度来说Shannon小波与本文所提出的新方法之间适性更高。
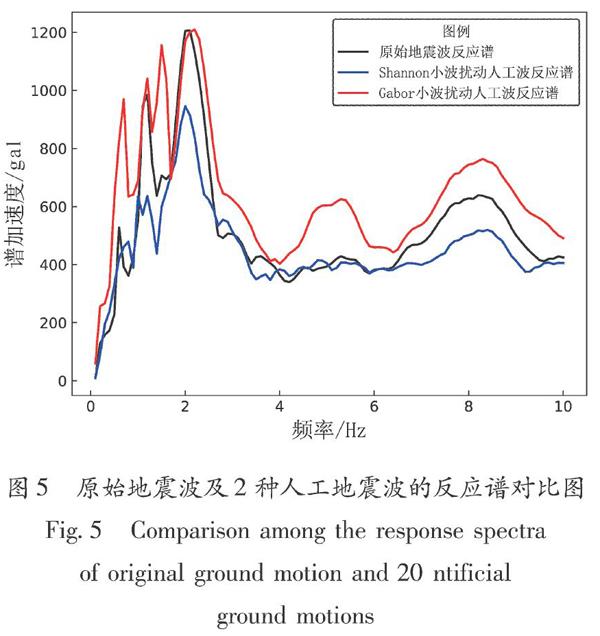
Shannon小波和Gabor小波扰动产生的人工波各自对应的反应谱与原始自然波反应谱对比见图5所示。可以看到通过复连续小波变换的扰动,人工波与原始波的反应谱谱形在特定的频域范围内变化较大,这和本文通过生成人工波,提高设计地震波池多样性的目标是一致的。
通过鸟取地震的模拟算例可以看到,对于随机方法中不可避免的全时域扰动的问题,以及离散小波变换无法任意制定扰动时-频域的问题,本文方法都体现出了独特的优越性,扰动在0~15 s及45 s之后的幅值几乎为0,而且扰动所存在的时-频域也是连续的。
4 结论
针对使用信号处理方法扰动自然地震波生成新的人工地震波的问题,本文提出了一个新的计算方法,使复连续小波可以在任意指定的时-频域上修改地震波的相位谱从而产生人工波,这是传统方法所不具备的特性。在这个过程中目标域外的地震波在时-频域的幅值信息得到了保留,同时人工波的性质包括反应谱等较原始波都有了较大的改变。
本文还对比了扰动过程中使用Shannon小波和Gabor小波的优劣,其中Shannon小波对地震波能量的保留优于Gabor小波,Gabor小波則对非目标时-频域的噪音更小,出于研究人员及工程师对人工波在地震动能级上保持一致的需求,Shannon小波基是更好的选择。
在经验系数c的取值能显著影响本文方法的效果,如何选取一个更合理的经验系数还有待进一步研究。
参考文献:
胡聿贤,何训.1986.考虑相位谱的人造地震动反应谱拟合[J].地震工程与工程振动,6(2):37-51.
呂大刚,李晓鹏,王光远.2006.基于可靠度和性能的结构整体地震易损性分析[J].自然灾害学报,15(2):107-114.
张郁山,赵凤新.2014.基于小波函数的地震动反应谱拟合方法[J].土木工程学报,47(1):70-81.
Boore D M 2003.Simulation of Ground Motion Using the Stochastic Method[J].Pure and Applied Geophysics,160(1):635-676.
Cattani C.2008.Shannon Wavelet Theory[J].Mathematical Problems in Engineering,28(1):24-25.
Deierlein G G,Krawinkler H,Cornell C A.2003.A framework for performance-based earthquake engineering[C].New Zealand:2003 Pacific Conference on Earthquake Engineering.
Hata Y,Nozu A,Ichii K.2011.A practical method to estimate strong ground motions after an earthquake based on site amplification[J].Bulletin of Seismological Society of America,101(2):688-700.
Honda R,Ahmed T.2011.Design input motion synthesis considering the effect of uncertainty in structural and seismic parameters by feature indexes[J].Jouranl of Structural Engineering,137(1):391-400.
Honda R,Khatri P P.2012.Discrete analytic signal wavelet decomposition for phase localized in time-frequency domain for generation of stochastic signal with phase uncertainty[C].Lisboa:World Conference on Earthquake Engineering.
Kamae K,Irikura K.1998.Source model of the 1995 Hyogo-ken Nanbu earthquake and simulation of near-source ground motion[J].Bulletin of the Seismological Society of America,88(1):400-412.
Koller M G,Lachet C,Fourmaintraux D.1996.Seismic hazard assessment with the aid of Empirical Greens Functions[C].Mexico:Eleventh World Conference on Earthquake Engineering.
Lee T S.1996.Image representation using 2D Gabor Wavelets[J].IEEE Trans.Pattern Analysis and Machine Intelligence,18(10):15-27.
Phase Randomization of Ground Motions with Arbitrary Time-frequencyRange Using Complex Continuous Wavelets
XIE Haoyu1,HONDA Riki2,ZHENG Wanshan1
(1.CMCT Research & Design Institute Co.,LTD,Chongqing 400060,China)(2.Graduate School of Frontier Science,The University of Tokyo,Kashiwa 277-8561,Chiba,Japan)
Abstract
For dynamic analysis,selection of input ground motions is of huge importance.The diversity of the set of input ground motions could be enhanced by simulating the artificial ground motions from natural earthquakes.A methodology utilizing complex continuous wavelets to simulate artificial ground motions areput forward,taking the 2000 Tottori earthquake(MW6.7)as aresearch target,and the characteristics of the Shannon wavelet and the Gabor wavelet are compared in the article.The result shows that the new methodology could have time-frequency domain arbitrarily oriented,and the Shannon wavelet is the optimal choice as it could maintain the power better than the Gabor wavelet.
Keywords:seismic design;artificial ground motion;wavelet transform;input ground motion

