WBK方程的分岔与行波解
韩青秀,刘红霞,伍 芸
(贵州师范大学 数学科学学院,贵州 贵阳 550025)
1 研究背景和预备知识
考虑如下的WBK方程[1-2]:
(1)
这是一个浅水波方程,已经被广泛地应用于物理学的许多分岔,在物理和数学中都有很大的作用,特别是它的解,可以帮助人们解释一些物理现象.许多学者已用不同的方法经研究了(1+1)维的WBK方程,例如扩展的辅助方程方法[3]、其次平衡法[4]、最优同伦渐近方法(OHAM)[5]、广义统一方法(GUM)[6]求解变系数等,在这里主要运用动力系统定性理论和分岔方法[7-13]研究.
为了研究式(1)的行波解,设c是波速且c>0,令u(x,t)=φ(ξ),H(x,t)=ψ(ξ),ξ=x-ct并代入式(1)可得:
(2)
对式(2)中的第1个方程积分,得:
(3)
积分常数为g.将式(3)代入式(2)中的第2个方程:
2(a+b2)φ‴-3φ2φ′+6cφφ′-2(c2-g)φ′=0
积分上式,并令积分常数为零,得到:
(4)
令φ′=y,得到下面的平面系统:
(5)
很明显,系统(5)的Hamiltonian函数为:
(6)
令:
f(φ)=φ3-3cφ2+2(c2-g)φ,Δ=c2+8g
显然,有下面的结果:
(1)当Δ>0时,f(φ)有3个零点φ0,φ1,φ2,它们的表达式为:
(2)当Δ=0时,f(φ)有2个零点φ0,φ*,它们的表达式为:
(3)当Δ<0时,f(φ)有1个零点φ0,它的表达式为:φ0=0.

其中θ=a+b2.根据动力系统定性理论[6],有如下结论:

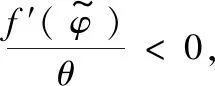
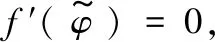
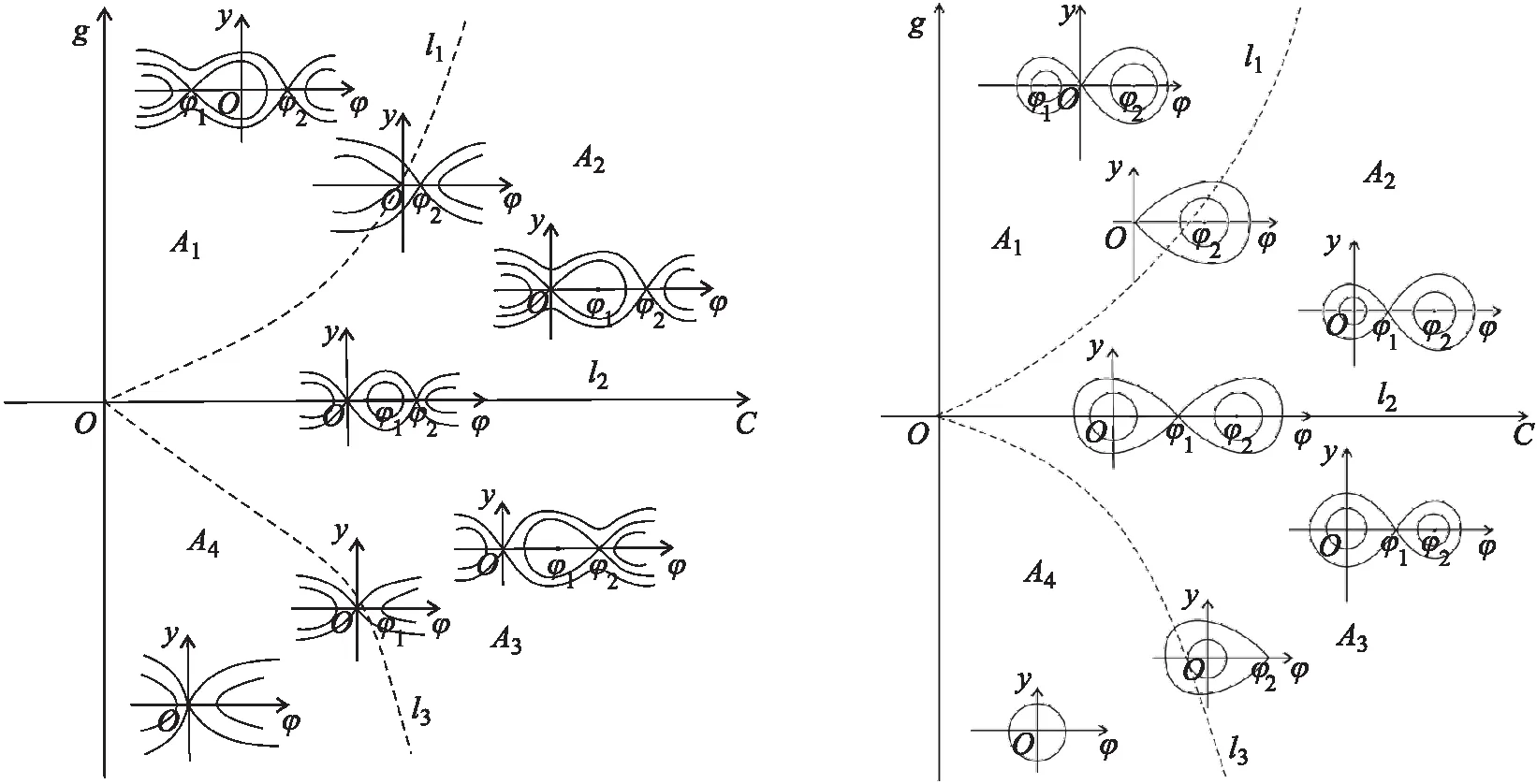
在c-g参数平面,令l1、l2和l3分别表示下面的3条曲线:
令Ai(i=1,2,3,4)表示被l1、l2和l3及坐标轴包围的区间,见图1.
2 扭波的分岔
接下来,将展示扭波可以由其他3种波分岔得到.
2.1 来自于钟形孤立波的分岔
命题1当θ>0且g (7) (8) θ>0 θ<0图1 系统(5)的分岔相图Fig.1 Bifurcation phase portraits of formula (5) 这些解有着如下的性质: (9) (10) 它们分别表示1个扭波和反扭波. (11) 在情形1中,当(c,g)属于A2区域且g→0+时,这2个钟形孤立波相应变成扭波式(9)和反扭波式(10),对此变化过程,见图2和图3. 证明:在式(6)中,令H(φ,y)=H(0,0),则有: (12) (13) 其中v是任意常数.将式(13)完全积分并解出φ,则有: (14) (a)g=1/32 (b)g=10-3 (c)g=10-4 (d)g=10-6图2 当c=1,g→0+时,的变化过程(钟形孤立波分岔为扭波)Fig.2 When c=1 and g→0+, the change process(The kink wave is bifurcated from the bell-shaped solitary wave) (a)g=1/32 (b)g=10-3 (c)g=10-4 (d)g=10-6图3 当c=1,g→0+时,的变化过程(钟形孤立波分岔为反扭波)Fig.3 When c=1 and g→0+,the change process(The anti-kink wave is bifurcated from the bell-shaped solitary wave) 在式(7)和式(8)中,令g=0时,则可以得到式(9)和式(10).由此可证明命题1的(1). 因此,可证明命题1的(2)和(3). 特别地,在情形1中,当(c,g)属于A3区域且g→0-时,这2个爆破波相应变成扭波式(9)和反扭波式(10),对此变化过程,见图4和图5. 类似于命题1的证明,可以得到命题2的结果. (15) (16) 特别地,当g→0-时,这2个峡谷形孤立波相应变成扭波式(9)和反扭波式(10),对此变化过程,见图6和图7. (a)g=-1/9 (b)g=-10-3 (c)g=-10-4 (d)g=-10-6图4 当c=1,g→0-时,的变化过程(爆破波分岔为扭波)Fig.4 When c=1 and g→0-,the change process(The kink wave is bifurcated from the blow-up wave) (a)g=-1/9 (b)g=-10-3 (c)g=-10-4 (d)g=-10-6图5 当c=1,g→0-时,的变化过程(爆破波分岔为反扭波)Fig.5 When c=1 and g→0-,the change process(The anti-kink wave is bifurcated from the blow-up wave) (a)g=-10-2 (b)g=-10-3 (c)g=-10-4 (d)g=-10-6图6 当c=1,g→0-时,的变化过程(峡谷形孤立波分岔为扭波)Fig.6 When c=1 and g→0-,the change process(The kink wave is bifurcated from the valley-shape solitary wave) (a)g=-10-2 (b)g=-10-3 (c)g=-10-4 (d)g=-10-6图7 当c=1,g→0-时,的变化过程(峡谷形孤立波分岔为反扭波)Fig.7 When c=1 and g→0-, the change process(The anti-kink wave is bifurcated from the valley-shape solitary wave) 证明:当(c,g)属于A3时,(φ2,0)在它的左边有1条轨线Γ和它相连,见图8. 图8 Γ的轨线相图Fig.8 The orbital diagram of Γ 在式(6)中,令H(φ,y)=H(φ2,0)=h2,则有: (17) (18) 将式(18)完全积分并解出φ,则有: (19) 其中η=η(v)是任意常数.从式(19)中可以得到形如式(15)和式(16)的解. 令g→0-,则有: 当g→0-时,积分以后可以得到扭波式(9)和反扭波式(10). 因此,证明了命题3. 命题4当θ<0且g (20) (1)如果(c,g)属于l1,那么uc表示周期爆破波解;(2)如果(c,g)属于A2,那么uc表示周期波解. 特别地,当g→c2-时,周期波就分岔成了周期爆破波.对此分岔过程,见图9.当g→0+时,周期波变成了线波u=2c,对此分岔过程,见图10. 令g→c2-,则有: 有: 至此,证明了命题4. (a)g=c2-10-1 (b)g=c2-10-2 (c)g=c2-10-3 (d)g=c2-10-5图9 当c=1,g→c2-时,uc的变化过程(周期波分岔为周期爆破波)Fig.9 When c=1 and g→c2-, the uc change process(The periodic blow-up wave is bifurcated from the periodic wave) (a)g=10-1 (b)g=10-2 (c)g=10-3 (d)g=10-5图10 当c=1,g→0+时,uc的变化过程(周期波分岔为线波)Fig.10 When c=1 and g→0+, the uc change process(The periodic wave becomes the trivial wave) 该文主要研究了WBK方程的分支现象和一些精确行波解,通过Maple得出系统的图形的变换,利用动力系统的定性理论判断系统奇点的类型,利用积分公式求解出行波解,并且揭示了2种分岔现象.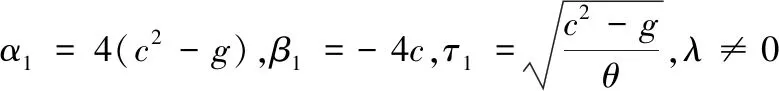
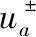
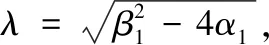

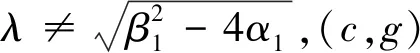




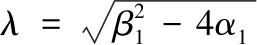
2.2 来自于爆破波的分岔
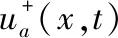

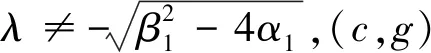
2.3 来自于峡谷形孤立波的分岔





3 光滑周期波的分岔

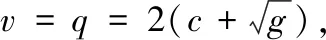
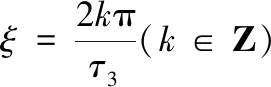


4 结 论

