基于反距离加权随机森林的空间推测方法研究

焦思佳，吴田军，董世英，王长鹏

(长安大学 理学院，陕西 西安 710064)

0 引 言

20世纪60年代，以卫星定位系统、地理信息系统和遥感为支撑的空间信息技术逐渐发展起来，大量带有空间位置的数据被采集、处理并应用[1-2].相比于其他数据，空间数据因其时空相关性的特性，难以使用变量独立性假设的经典统计学方法，这使得几何空间中的牛顿推测等方法并不适用.1970年，Toblert[3]提出“地理学第一定律”，为空间数据的分析和应用提供了理论基础.在该领域，将离散点的测量数据转化为连续数据表面的空间推测是最为重要研究问题之一.经过几十年的持续发展，空间推测算法不断完善，并逐渐被应用到土壤水质、海洋环境、地质勘探、空气质量等诸多领域.但随着生产力的进步，社会以及经济生活对地理空间信息的精细性、时效性需求进一步凸显，这也倒逼各领域对空间推测算法提出更高的要求.因此，进一步发展空间推测模型，提升专题制图水平，具有重要现实意义.

目前，典型的空间推测方法大致可分为以下四类：(1)以反距离加权(Inverse Distance Weighted, IDW)为代表的确定性推测方法.IDW[4]是一种以距离作为权重的滑动平均加权推测方法，伴随着实际问题数据集的复杂性，基本的IDW满足不了空间推测需求，因此，在之后的研究中其经过不断改进发展，例如，王可伟等[5]在IDW中引入圆形窗口与夹角权因子，有效地提高建模的效率与精度.(2)以克里金(Kriging)为代表的地统计推测方法.克里金方法是1951年南非地质学家克里金(Krige)首次提出，后经法国著名数学家Matheron发展深化[6].由于克里金将空间相关性考虑在内以及使用克里金标准偏差量化推测误差这一优点，成为主流方法，随后也有一定的扩展，例如泛克里金(Universal Kriging, UK)[7]、具有外部漂移的克里金(Kriging with External Drift, KED)[8].刘婕[9]运用UK推测北京市六城区预估点的PM2.5，并验证统计值通过F检验及t检验.邬春明等[10]提出基于线性动态变化因子结合柯西变异粒子群算法对变异函数的拟合模型参数进行最优化估计，同时在适应度函数中引入克里金地理权重来增强变量的空间相关性，有效地提高推测精度并改善变异函数拟合曲线误差过大的问题.(3)以回归克里金(Regression Kriging, RK)代表的组合方法.Mohanasundaram等[11]运用RK推测预估点的地下水位，证明推测结果优于其他克里金方法.当然，机器学习(Machine Learning, ML)的不断发展同时促进RF与克里金组合，例如，Li等[12]将RF、广义线性模型与地统计方法组合，证明这些组合方法比传统模型精度更高.(4)以ML为代表的推测方法.2001年，Breiman[13]提出RF，并且说明RF适用于回归问题，同年，Rigol等[14]首次提出在运用神经网络(Neural Network, NN)推测时，将回归趋势与空间关联性一同考虑.2011年，Li等[15]提出将RF应用到环境变量的空间推测中，并与普通克里金(Ordinary Kriging, OK)、IDW组合，表明提出方法的有效性以及对输入变量的敏感性.WU等[16]提出基于地理图斑的RF空间推测方法，相较于传统的基于规则网格的方法，该方法在推测精度方面有一定的提高.尽管ML在空间推测方面非常成功，但在直接使用该类技术时大多没有考虑到观测值是具有地理空间自相关的.因此，在之后的研究中，经度、纬度等地理背景相关的推测因子被引入到模型构建中.Behrens等[17]提出将地理空间自相关的欧式距离与ML组合，并证明比RK、地理加权回归(Geographically Weighted Regression, GWR)等方法更具优势.Hengl等[18]在2018年提出“Random Forest for spatial prediction (RFsp)”模型，其以预估点到样本点的缓冲距离作为推测因子，证明其相较于线性地统计建模与克里金等传统方法，提高了推测精度.2020年，Sekulic等[19]提出“Random Forest Spatial Interpolation (RFSI)”模型，其将邻近点的观测值以及到预估点的距离作为推测因子引入模型中，并验证RFSI的推测结果优于克里金以及RFsp.

RFsp、RFSI分别以预估点与所有样本点的缓冲距离、邻近点的观测值与其到预估点的距离作为推测因子来弥补RF在空间推测方面的不足，但RFSI对于距离的应用仍存在潜在问题，且模型中运用的邻近点被考虑在同一等级水平中，这并未充分体现地理学第一定律的空间相关性原则.有鉴于此，针对RFSI的上述不足，本文提出基于位置距离的反距离加权随机森林(Random Forest with Inverse Distance Weighted based on location distance, RFIdw)模型，主要针对样本点的观测值与到预估点的距离实施反距离加权策略，将距离因素的远近考虑在内，离预估点越近的样本点将赋予更高的权重.另外，由于反距离加权组合之后，建模过程中的推测因子减少，随机森林的mtry等参数设置将会在更小的范围，从而减少模型拟合时间.本文通过Spatial Interpolation Comparison 97 (SIC97)数据对RFIdw与RK、RFsp、RFSI加以比较，验证RFIdw在空间推测方面的有效性.

1 研究区及数据集介绍

降水量由于受地区、海拔等各种因素影响，往往呈现出复杂的空间分布趋势，因此，在空间推测研究方面被广泛应用.本文通过SIC97数据集所对应的研究区以及包含的具体数值加以介绍，更好地阐明RFIdw模型的应对问题.

1.1 研究区概况

本文选取瑞士作为研究区域如图1所示，该区域地处欧洲中南部，位于北纬45°49′～47°48′，东经5°57′～10°29′之间，国土面积约为4.1万km2，地域虽小，但各地气候差异很大.阿尔卑斯山由东向西伸展，形成了瑞士气候的分界线，以北地区受温和潮湿的西欧海洋性气候和冬季寒冷夏季温热的东欧大陆性气候的交替影响，变化较大；以南地区则属地中海气候，全年气候宜人.全国年降水量在 1 000～2 000 mm 之间，3/4地区平均年降水量超过 1 000 mm.该区域的降水深受地形的影响，高山峻岭处降水量远远超过中部高原一些地区及河谷地带.

图1 瑞士DEM与站点图Fig.1 Station locations in Swiss on top of DEM of study area

1.2 实验数据集

本文数据集包括了站点观测的降水量数据集、DEM、CHELSA(Climatologies at high resolution for the earth’s land surface areas)降水量数据等，具体说明如下.

1) 降水量数据.研究采用的降水量数据是1997年4月在环境研究所(Joint Research Centre, EC, Ispra)放射性环境监测机构下组织的一项活动中所收集，该数据集包括1986年5月8日测量的100次降水量以及估计的367个站点降水量，单位为 0.1 mm[20].具体信息如表1所示.

2) DEM数据.研究采用的DEM数据是从https://www.usgs.gov/获取，空间分辨率为 1 km，具体信息如图1所示.

3) CHELSA降水量数据.由于向上的气流加剧山顶斜坡位置的云和降水形成，而局部环流系统沿山谷轴线的下沉分支导致云溶解相应地降低谷底的降水量这种特殊的地形降水效应，阿尔卑斯山山顶可能会有较高的降水量.CHELSA降水量数据则是对其降水效应进行近似，并将其运用到ERA-Interim气候再分析降尺度模型中输出的结果[21].

2 空间推测方法与模型

2.1 空间推测方法

目前，空间推测技术的发展主要分为两个阶段，前一阶段主要是克里金等传统方法的发展，但其理论性高，有诸多假设条件，并且由于数据集的复杂性，很难满足.因此，后一阶段二十一世纪初兴起的ML弥补了传统方法的部分缺点，引发了空间推测方法的进一步提升，并被广泛应用到各领域.而本文就是在RFSI模型的基础上加以改进，提出RFIdw模型.

2.1.1 RFSI方法与模型

由于RF中忽略了样本点之间的空间自相关性，可能会导致推测结果不准确，为弥补这项不足，构建了RFSI模型，其是在RF的基础上引入邻近点的观测值以及到预估点的水平位置距离，公式表达式如下：

(1)

式中：covj(s0)(j=1,…,m)为预估点s0类似海拔、温度、NDVI等的推测因子，z(si)为第i个邻近点si的观测值，dloci(i=1,…,n)是第i个邻近点si与预估点s0之间的水平位置距离.RFSI将邻近点的信息考虑在内，相比RF、RFsp更加接近空间推测原理.

2.1.2 RFIdw方法与模型

RFSI采用邻近点的观测值以及到预估点的水平位置距离反映推测位置的信息，但是由于模型构建的最终目的是实现降水量的精准推测，而在RFSI模型训练的过程中，当邻近点到预估点的距离小于或者大于一定范围时，推测的过程以相同的方式进行，这将导致推测结果出现偏差.因此，为减小距离对模型训练过程中的影响以及充分体现地理学第一定律，本文在RFSI的基础上加以改进提出RFIdw模型，其大致可以分为反距离加权和模型构建两部分，核心思想是针对RFSI中选取的邻近点的观测值以及到预估点的距离反距离加权，其组合值与原有的环境推测因子构建形成RFIdw模型.模型的表达式为：

(2)

(3)

对于ωi(s0)，其表达式为：

(4)

(5)

式中：(xi,yi)为第i个邻近点si的位置，(x0,y0)为预估点s0的位置，l为反距离的指数.结合SIC97降水量数据，本文基于RFIdw模型执行空间推测过程的算法伪代码如表2所示.

2.2 模型评价标准

为验证RFIdw模型推测结果的效性以及准确性，选取RK、RFsp、RFSI三种方法与其进行比较，并利用平均绝对值误差(Mean Absolute Error, MAE)、均方根误差(Root Mean Square Error, RMSE)、判定系数(Coefficient of Determination,R2)、一致相关系数(Concordance Correlation Coefficient, CCC)这四个评价标准加以比较，公式如下：

(6)

(7)

(8)

(9)

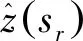
表2 基于RFIdw模型的空间推测算法伪代码

3 SIC97数据空间推测结果分析与讨论

3.1 空间推测制图结果分析

基于RK、RFsp、RFSI以及RFIdw模型的空间推测结果以及不确定性如图2、图3所示，其中(d)为RFIdw的推测结果图与不确定性图.由图2(d)推测结果可知，降水量呈由西南角到东北角带状分布趋势，其中，瑞士西部区域降水量较多，中部区域降水量较少.由图3(d)的不确定性结果可知，绝大部分区域推测标准差保持在较小的水平，较大的区域主要在瑞士的东部区域，结合图1的DEM数据可知，瑞士的东南部区域海拔比其他区域高，导致站点数据稀缺，以致空间推测方法难以在这一区域捕捉到有效信息，如需更准确地掌握该区域的降水量情况，还需要进一步获取样本点的信息.

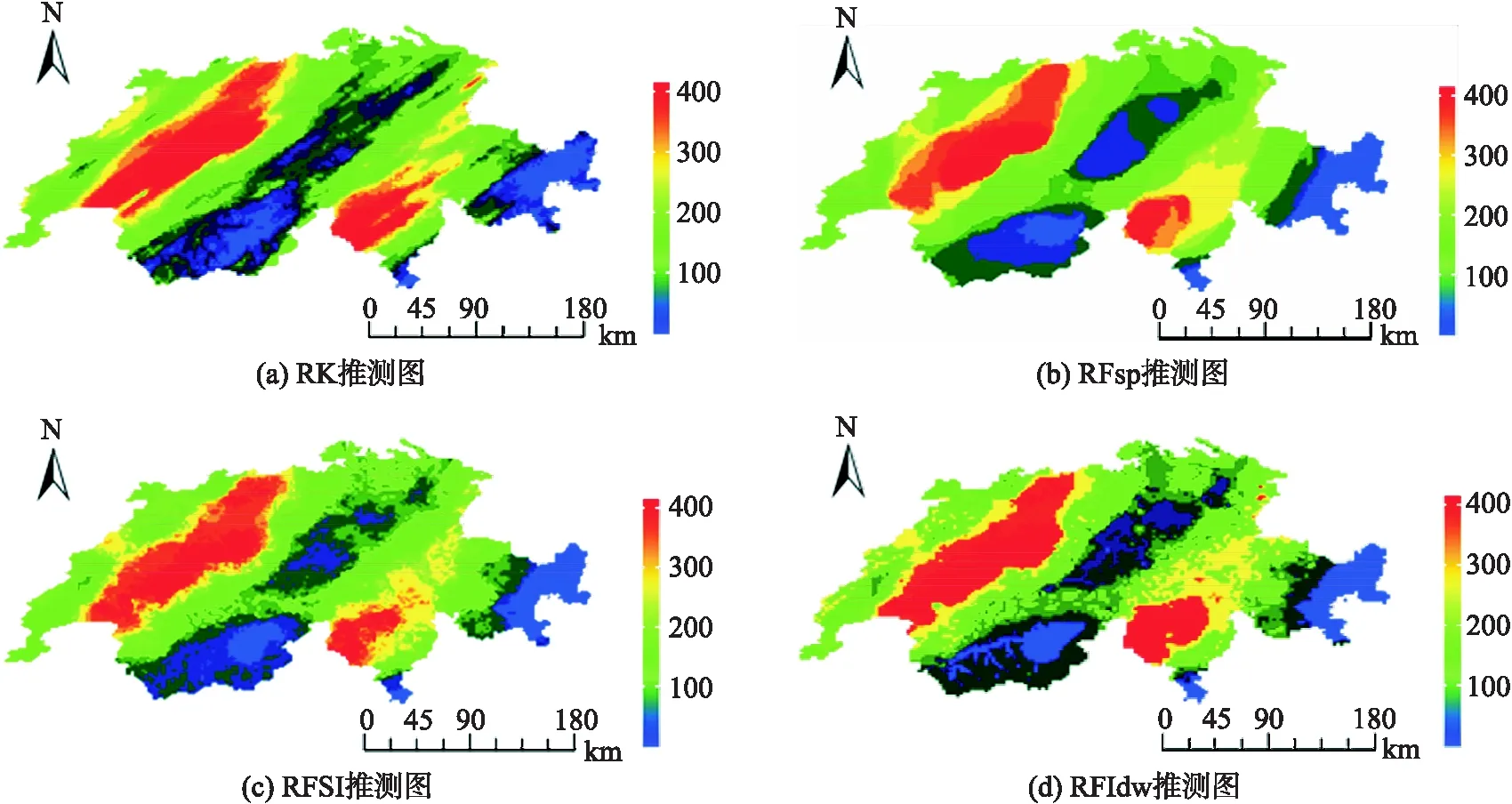
图2 RK (a)、RFsp (b)、RFSI (c)、RFIdw (d)瑞士降水量推测图Fig.2 RK (a)，RFsp (b)，RFSI (c)，RFIdw (d) spatial prediction results of Swiss rainfall

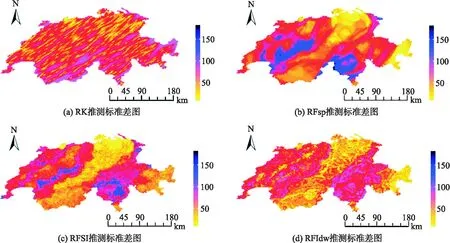
图3 RK(a)、RFsp(b)、RFSI(c)、RFIdw(d)瑞士降水量推测标准差图Fig.3 RK(a)，RFsp(b)，RFSI(c)，RFIdw(d) Swiss rainfall prediction standard error

结合RK、RFsp、RFSI空间推测以及不确定性图与RFIdw相比较，降水量的推测结果总体趋势大致相同，但在局部个别区域中差异明显，主要集中在瑞士阿尔卑斯山以南海拔较高的区域，相比于RFsp、RFSI，RFIdw推测结果更加精确.在不确定性方面，本文以标准差为评价指标，其中，RK标准差的表达式为：

(10)

式中：C0、C1是变异函数的参数，c0是预估点与样本点之间的协方差向量，q是推测因子的n×(p+1)维矩阵，C是样本点之间n×n维的协方差矩阵，q0是预估点s0处的p+1维推测因子向量，对于RFsp、RFSI、RFIdw的标准差则为：

(11)

相对RFsp、RFSI、RFIdw三种方法的标准差图，RK标准差相对较小，但是其标准差呈现均匀分布的趋势，对不确定信息的衡量包含的信息相对较少，即特殊点(预估点周围样本点相对较少)的标准差无法更加标准地度量.基于RF的三种空间推测方法RFIdw、 RFsp、RFSI在推测标准差方面不同之处主要集中在瑞士偏东南的区域中，RFsp的标准差基本保持在150相对较高的水平，RFSI虽然减小部分区域的标准差，但仍有小部分区域保持在较高水平，相对于RFsp、RFSI，RFIdw的误差对于东南的区域明显降低.结合四种空间推测方法的推测结果与不确定信息来看，RFIdw推测结果保持着较高的精度，并且在不确定性方面，RFIdw与RFsp、RFSI相比，标准差更小，与RK相比，不确定性更加具有信息性，因此，RFIdw对于空间推测的结果更加合理.

3.2 交叉验证结果分析

本文提出的RFIdw模型与RK、RFsp、RFSI交叉验证结果如表3所示.对比发现，在推测精度方面，RK最大，RFsp最小；在推测标准差方面，则相反.此外，从图4观测值与推测值的相关图可得知，相较于RFIdw，RFsp、RFSI是相对分散的，同时证实了表3中RFsp、RFSI方法较高的RMSE，较低的R2、CCC.

表3 基于五折交叉验证四种推测方法的精确度

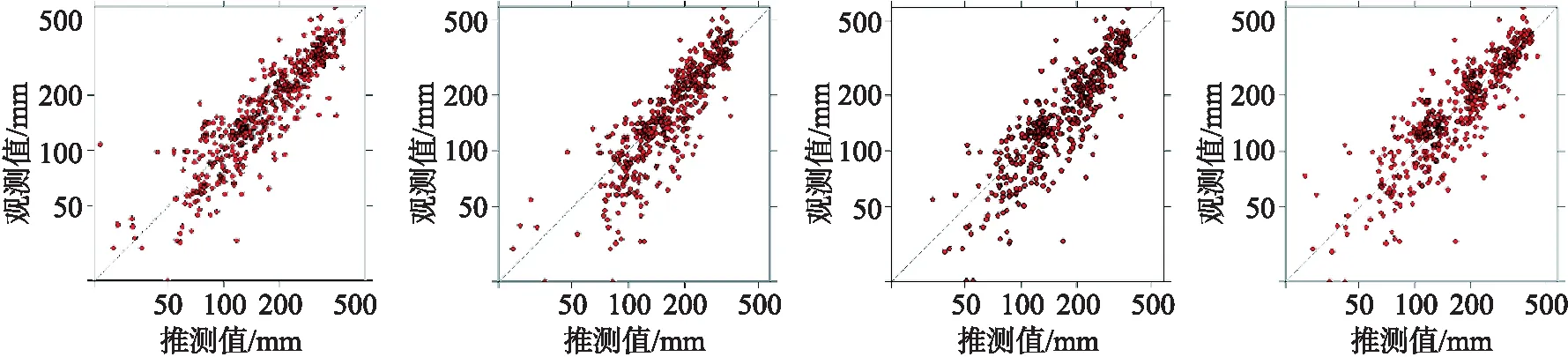
(a) RK相关图 (b) RFsp相关图 (c) RFSI相关图 (d) RFIdw相关图图4 RK (a)、RFsp (b)、RFSI (c)、RFIdw (d)基于观测值与推测值的相关图Fig.4 RK (a),RFsp (b),RFSI (c),RFIdw (d) correlation plots based on observations and predictions

进一步分析，由于RK是克里金与多元线性回归的组合，其具有克里金平稳性、残差服从正态分布等假设条件，虽然在SIC79数据推测结果方面，其表现出更高的推测精度，但是，在复杂的实际问题中，这些理想化条件往往很难满足，以致于结果可能会出现偏差；RFsp虽然将空间位置关系考虑在内，但缓冲距离计算的过程往往缓慢，并且在本次实验中，并没有很高的推测精度；RFSI将样本点之间的空间自相关性考虑在内，但是模型训练过程中距离的应用可能导致推测结果的偏差.因此，相较于RK、RFsp、RFSI，RFIdw在空间推测方面不失为一种好的选择.

4 总结与展望

为获得精确的空间推测结果，本文发展了一种基于水平位置距离的反距离加权随机森林RFIdw模型，不仅考虑了邻近点的观测值以及到预估点的距离，并对每个邻近点赋以权重，从而更好地体现了地理学第一定律的思想.为了验证RFIdw在空间推测准确性与不确定性等方面，本文通过SIC97数据进行了对比实验，将RFIdw与RK、RFsp、RFSI这三种空间推测模型加以比较，从推测制图效果、不确定性以及交叉验证精度分析，RFIdw相较于RK，减少了例如克里金模拟变异函数等的过程；相较于RFsp，减少计算缓冲距离的过程，提高模型训练的速度；相较于RFSI，有效地解决模型训练过程中应用距离的问题，并且得出RFIdw在推测结果方面优于RFsp、RFSI这两种方法，在不确定性表达方面更加具有信息性.

虽然本文中的RFIdw模型在空间推测方面有一定的有效性与准确性，但仍存在问题亟待解决：首先，针对本文的推测结果，RFIdw的结果稍逊于RK，可能由于在RFIdw模型中考虑的只是简单的反距离加权，因此，未来应该对权重设计开展更加深入的研究，例如引入邻近点之间的距离以及对权重指数的复杂化[22]，使权重更加合理化；其次，本文对距离的刻画只是两点之间的水平位置距离，没有考虑到海拔等距离的因素，导致可能两点之间虽然几何空间中距离相近，但在地理空间中两点并不相似，以致选取的邻近点可能有失偏颇，今后可以考虑地理空间中的测地距离[23]；最后，对RFIdw模型的评价方面，目前只考虑了推测结果及其不确定性，今后还可考虑其他方面的因子，以便更加全面地衡量模型性能.