基于GTMOPSO算法的交直流混合微网优化配置研究
焦艳丽,樊小朝,2,史瑞静,2,王维庆,刘少名,于春伟,陈 军,高 超,郝雁峰
(1.新疆大学 电气工程学院,新疆 乌鲁木齐 830047; 2.新疆工程学院 新能源科学与工程系,新疆 乌鲁木齐 830023;3.新疆金风科技股份有限公司,新疆 乌鲁木齐 830026)
0 引 言
微电网是集发电、配电和用电一体的综合电网系统,可以实现分布式电源产生的电能直接供给用户使用.合理利用微电网被认为是促进分布式能源友好并网和多能互补集成优化的有效手段[1-2].通过对微电网中的各设备容量进行合理优化,可使微电网更加经济、可靠和环保.文献[3]提出一种改进的风光储系统容量优化配置方法,针对独立和并网的不同模式,优化微电网中的风、光、蓄电池的供电能力;文献[4]以经济性和电力平衡稳定为优化目标,利用改进的粒子群算法对所提微电网容量进行优化;文献[5]以经济性为目标,综合考虑充放电效率、全寿命周期成本和荷电状态,提出一种基于改进希尔伯特-黄变换的混合储能容量优化配置方案;文献[6]以成本最小为目标,引入需求侧响应概念,对独立的风、光、储微电网进行容量优化配置,提高负荷需求与供电的匹配度,建立包含经济性和环保性的多目标优化模型,通过队列竞争优化算法对配置结果进行求解;文献[7]提出一种考虑需求侧响应的孤岛微电网容量配置模型,以全寿命周期成本最低为目标,采用粒子群算法进行求解;文献[8]以满足偏远地区电力用户需求为目标,综合考虑了投资总成本、电力平衡状态、能源出力波动等优化目标,提出离网型风/光/储微电网的优化方案,采用具有自适应交叉和变异操作的改进遗传算法进行求解.
上述研究大多以风、光、蓄电池装置相互结合进行容量的配置优化,对引入氢储能装置以及将用户侧用电行为加入到微电网容量配置优化的决策较少.而由于混合储能装置的引入,使得微网拓扑结构趋于复杂,运行模式也更加趋向多样化.因此,风光出力的随机性和波动性、用电负荷的不确定性及微网系统的复杂性对微网的容量配置都带来了极大的挑战.
基于此,本文首先提出了包含氢储能和蓄电池储能的多级混联储能系统(Hybrid Energy Storage System, HESS),采用交直流混合策略实现交流侧电力供交流负载使用,直流侧电力供直流负载使用,交直流母线间通过换流设备进行能量交换,“闲电”通过HESS系统储存,“余电”进行上网处理;然后在用户侧引入分时电价机制,考虑到用户的负荷量的多时段响应机制,引入电量电价间平衡关系及多时段弹性矩阵,将用户侧的负荷调控纳入到系统容量配置决策中,鼓励用户积极参与到微电网优化问题;接着提出基于博弈理论和混沌映射多目标粒子群优化算法(Game Theory Multi-Objective Particle Swarm Optimization Algorithm, GTMOPSO),引入博弈理论和混沌映射有效改善粒子群算法容易陷入局部最优解的缺陷,以更好地保护算法多样性,使用经典测试函数ZDT2、ZDT3验证改进算法的优越性;最后通过实际的风光和负荷数据制定多模式运行策略和不同的配置方案,对微电网的等年值成本和换流损耗进行分析.
1 微网系统结构
本文所研究的微电网系统结构如图1所示.光伏机组与风电机组分别与直、交流母线相连,为直、交流负载提供电能,在最大化消纳可再生能源发电的前提下减少系统内部的换流设备.储能装置包括以蓄电池为主的电化学储能装置和以燃料电池、储氢罐和电解槽3者耦合形成的氢储能装置.
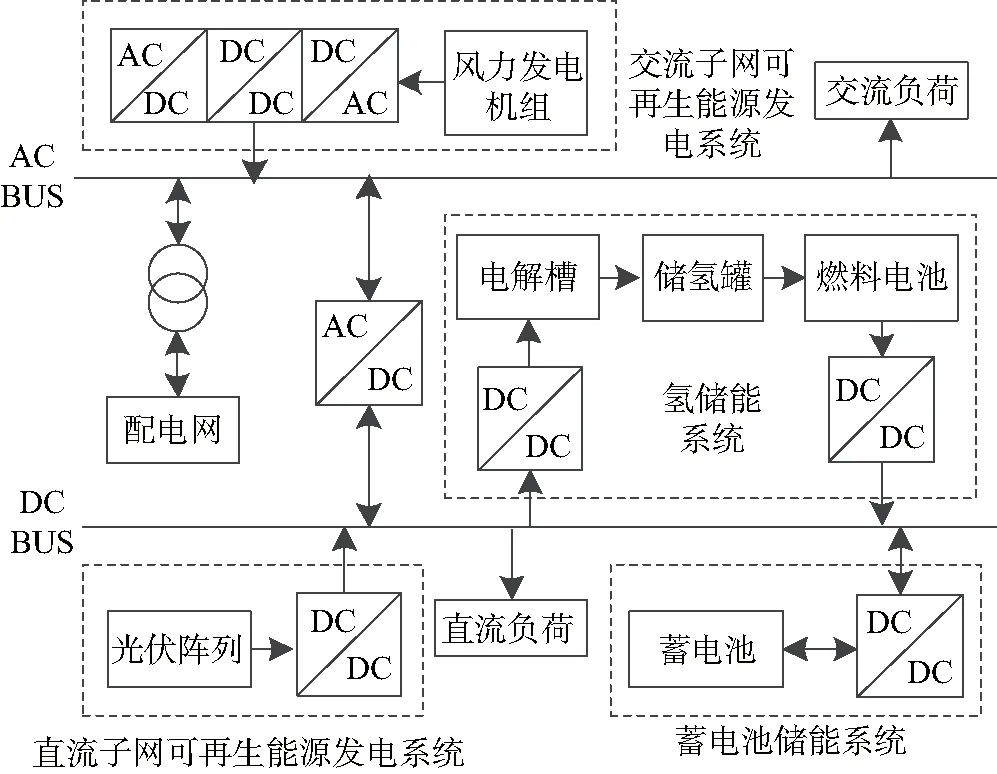
图1 HESS交直流混合微网结构 Fig.1 Structure of HESS AC-DC hybrid microgrid
1.1 微网电源模型
1.1.1 风机模型
风机的出力主要与所处环境风速有关,其数学模型[9]为:
(1)
式中:PW为风机输出功率,kW;Pr为风机额定功率,kW;vci为风机切入风速,取 3 m/s;vr为额定风速,取 6.5 m/s;vco为切出风速,取 20 m/s.
1.1.2 光伏发电模型
光伏电池输出功率受所处环境的辐照强度和温度影响,数学模型[10]为:
(2)
式中:PPVR为光伏组件额定输出功率;S(t)为太阳能辐射强度,W/m2;SST为太阳能标准辐射强度,取 1 000 W/m2;λ为温度系数,本文取λ=0.004 85/℃;Ta(t)为组件实际环境温度,℃;TN为标准工作温度,取 25 ℃;ηPv_dc-dc为光伏逆变器转化效率,此处取值0.9.
1.2 混合储能系统模型
氢储能系统具有较强的多能联供能力,可以改善能量失衡,而微电网系统可以促进能量平衡并进行综合调控,因此氢储能系统在微电网系统中具有广阔的前景[11].在HESS系统中,风、光出力首先满足蓄电池的容量约束目标,然后将多余的电能利用电解槽转化为氢气储存.当蓄电池储存电量不够用户使用时,由燃料电池将储氢罐中的氢气转化为电能以供使用.
1.2.1 蓄电池模型
根据能量守恒定理,蓄电池充放电时的能量[12]可分别表示为:
蓄电池充电时:
Ebat(t)=Ebat(t-1)(1-δ)+Pch(t-1)ηchηbat_dc-dcΔt
(3)
蓄电池放电时:
(4)
式中:Ebat(t)为t时刻蓄电池储存的能量,kW·h;δ为蓄电池自放电率,取0.04/d;Pdh为蓄电池充电功率,kW;Pch为蓄电池放电功率;ηch为蓄电池充电效率,ηdh为蓄电池放电效率,ηbat_dc-dc为蓄电池的换流器效率,均取0.9;Δt为时间步长,本文取值为 1 h.
1.2.2 氢储能系统模型
氢储能系统中,选取质子交换膜燃料电池和质子交换膜电解槽,其输出率可分别表示为:
PEb2Hs=PEbηEb
(5)
PFc=PHs2FcηFc
(6)
式中:PEb为输入功率;ηEb为电解槽效率,取0.8;PHs2Fc为储氢罐与燃料电池的交互功率;ηFc为质子交换膜燃料电池的工作效率,取0.8.
为了更好地管理和控制储氢罐的运行状态,以燃料电池和电解槽侧充放电过程中的功率值计算储精罐的剩余容量,储氢罐储能的数学模型可表示为:
(7)
式中:EHs(t)为t时刻储氢罐储存的能量,kWh;ηEb_dc-dc、ηFc_dc-dc分别为电解槽和燃料电池的换流器工作效率,均取0.9.
综上,电解槽与燃料电池的最大输出功率为:
(8)
(9)
式中:CEb为电解槽容量,kW;CFc为燃料电池容量,kW;EHs为储氢罐容量;EHsmax为储氢罐最大储能容量;EHsmin为储氢罐最小储能容量,储氢罐容量单位均为kW·h.
1.3 分时电价模型
分时电价下,用户的负荷量不仅是对当前时段电价的响应结果,还会受到其他时段电价的影响,即为多时段响应[13].基于此,本文引入电量电价间平衡关系以及基于分时电价的弹性矩阵以更好地描述用电行为,通过分时电价机制对负荷使用情况进行处理,以进一步使交直流负荷与风电和光伏机组出力情况更匹配.其中,电量电价弹性可表示为:
(10)
式中:r为电量电价弹性;L和e分别为用电量与电价;ΔL、Δe分别为其对应的变化量.
为了更好地描述由于分时电价实施时用户受其他阶段电价影响的用电量关系,提出基于分时电价的弹性矩阵R,具体表达式为:
(11)
式中:rPP、rff、rVV分别代表峰、平、谷时段自弹性系数,其余为互弹性系数.
在已知电量电价弹性矩阵的前提下,可得到用户各时段用电量与电价变化量之间的关系式:
(12)
式中:L0和LTOU分别代表施行分时电价前后各时段用电量,kW·h.;L0,P、L0,f、L0,V分别表示可进行负荷转移时段的初始用电量,kW·h.
2 微网优化配置模型
2.1 待优化变量
选取光伏电池容量Cpv、风电机组容量Cw、蓄电池容量Cba、燃料电池容量CFc、电解槽容量CEb、储氢罐容量EHs和换流器容量Ccon作为微网配置中待优化变量.
2.2 目标函数
微网系统优化目标包括经济性、环保性和供电可靠性等.本文所配置系统为并网型系统,未加入柴油发电机等备用电源,因此未考虑环保性目标,且将可靠性指标加入到了配置系统的约束条件中.因此,主要考虑所提微网系统经济性指标中的等年值成本F和交直流混合微网中交直流母线间的换流损耗Pt-loss作为待优化目标.
2.2.1 经济性指标
本文经济性指标即考虑全寿命周期的等年值成本F,详细目标函数为:
(13)
(14)
式中:CI为微网设备初始投资成本;R为系统寿命,取20年;r为贴现率,取0.04;C(k)为第k年的其他成本,包括各设备第k年的运行维护成本、置换成本等;B(k)为第k年的其他收入及支出,包括微网系统电能不足用户使用或满足使用后电量有盈余时产生的购售电成本、可再生能源发电的补贴收益以及各设备折现成本,万元;CRF(r,R)为资金收回系数.
2.2.2 换流损耗指标
本文微网采用交直流混合策略实现交流侧电力供交流负载使用,直流侧电力供直流负载使用,交直流母线间通过换流器进行能量交换,母线之间的换流损耗计算公式为:
Pt-loss=(1-ηcon)Pac/dc
(15)
式中:Pac/dc为交直流母线间换流功率;ηcon为换流器换流效率,取0.9.
2.3 约束条件
在微电网系统容量优化过程中,必须对各优化变量以及所优化目标值建立相应的约束,使其在约束范围内寻求最优值,保证优化结果的有效性.本节主要针对分布式电源出力、系统功率平衡、各设备装机容量、储能系统充放电深度以及系统的供电可靠性5个方面进行约束.
1)系统中分布式电源的出力约束不能大于其固定容量的额定输出功率:
(16)
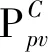
2)在交直流混合微电网中,由交流侧电源直接为交流负载供电,直流侧电源直接为直流负载供电,在微电网系统中的各微源与负荷之间需要有一个功率状态平衡约束,而交直流母线间通过进行能量传输,以维持交流子网与直流子网的功率平衡,微电网系统功率平衡约束为:
(17)
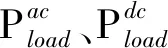
3)考虑到实际工程中受各种条件的限制,需要对微网内各分布式电源及储能装置装机容量范围约束.考虑到蓄电池和储氢罐的放电深度对设备的影响,进行储能装置容量配置时,留出一定的备用容量.各装置的配置容量约束为:
(18)
4)为提高实施分时电价时用户总体满意度,设置用户侧响应后单位时段用电费用不得高于响应前费用,具体约束为:
(19)
式中:e0为实施分时电价前的单一电价;ep、ef、ev分别表示峰、平、谷时段的电价,元/(kW·h);Lc0,h(t)、Lc,h(t)为实施分时电价前后的用电量,kW;Eh、E0,h为时间步长下分时电价后和分时电价前的用户购电成本,万元.
5)微电网系统的终极目标就是实现“自发自用,自治自理”,因此需要对整个系统的供电可靠率有较高的要求,本文将供电可靠性作为微电网容量配置的主要约束之一.将微电网年运行过程中总负荷需求量与分布式电源输出功率的差值同分布式电源输出功率的比值定义为负荷失电率(Load Power Shortage Rate, LPSR),具体表达式为:
(20)
式中:Pload、PDG为单位时间内交直流负荷总量以及风机和光伏系统输出功率总量.为使微电网有较高的供电可靠性,取LPSRmax=0.5%.
3 优化目标求解方法
微电网系统常见的配置方法包括分析法、配置软件求解法以及智能算法等,本文主要采用智能算法中需要较少预设参数、迭代更新方式和计算方式也较简单的粒子群算法(Particle Swarm Optimization, PSO)进行求解.
3.1 算法介绍
传统的PSO算法中,粒子的速度和距离更新公式[14]如下:
(21)
(22)
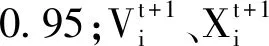
然而,用于解决复杂问题时,PSO算法容易出现粒子“早熟”现象(即陷入局部最优解),导致寻优效果较差.因此,在解决微电网容量优化问题中,需要对算法进行改进以更好获得本文优化变量和目标值最优解.
3.2 算法改进
基于以上分析,提出一种基于博弈理论和混沌映射的多目标粒子群优化算法,引入博弈机制[15]和混沌映射机制有效改善粒子群算法在寻优过程中易陷入局部最优解的缺陷.
博弈机制是用于解决粒子群优化算法的一个变体,通过提取的两个粒子进行博弈竞争,优胜的粒子将会引领失败的粒子前进从而更新粒子的速度和位置,直接过渡到下一轮循环,将每一个粒子作为最优解来带领其他粒子进行更新,不需要历史最优粒子一直引领,可以有效解决粒子全局寻优效果不佳问题.博弈机制的中心思想如图2所示,其中P(t)和P(t+1)分别表示进行粒子迭代更新前后的集合名称.
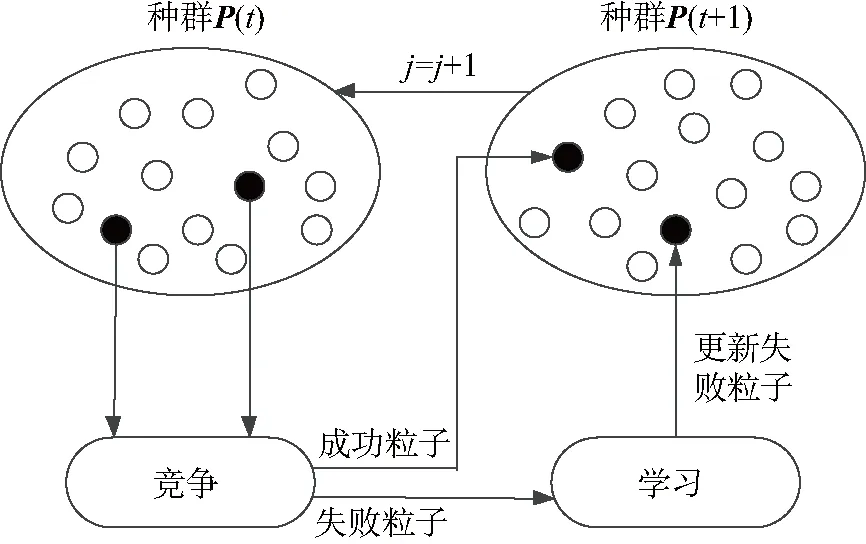
图2 博弈主要思想Fig.2 Main ideas of Game Theory
而博弈更新机制主要采取夹角角度比较,不再是以适应度数值进行比较,精英粒子a和b从精英集中被选出后与非精英粒子x进行博弈,比较所形成的夹角θa和θb的大小,形成角度小的粒子被定义为成功粒子,引导非精英粒子x进行位置和速度的更新,失败粒子继续向成功粒子学习,以更新自身粒子速度和位置,如图3所示,粒子a则为博弈成功粒子.
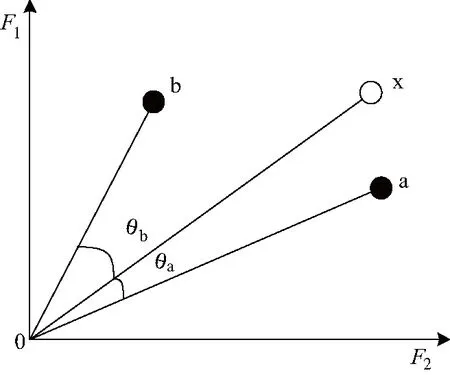
图3 两精英粒子进行博弈Fig.3 Game between two elite particles
精英粒子之间进行博弈和学习后进行粒子的速度和位置更新,公式如下:
(23)
Xd,i(t+1)=vd,i(t+1)+Xd,i(t+1)
(24)

混沌映射作为全局最优处理机制,可以有效地避免搜索过程中粒子陷入局部最优解的状况.本文采用的混沌映射公式[16]为:
(25)
式中:Xj是混沌数;j为迭代次数.
引入混沌机制和博弈理论机制后产生的新精英集内的粒子速度和位置更新公式为:
(26)
(27)
式中:c6和c7是[0,1]之间的随机产生的向量;Xs是上一次博弈成功粒子的位置;Xj是非精英粒子位置;vj是非精英粒子速度.
3.3 算法测试
通过以上2种改进方法,加强传统PSO算法的全局搜索与局部寻优能力.将改进后的基于博弈机制和混沌映射机制的GTMOPSO算法与PSO算法分别对经典的测试函数ZDT2、ZDT3[16]随机运行100次,所得函数逆代距的平均值和标准偏差的对比结果如表1所示.

表1 算法的测试函数逆代距平均值和标准偏差
从测试结果可以看出,GTMOPSO算法在两组测试函数中皆取得了最小的逆代距,逆代距值越小,算法得出的结果越优.且从图4中2种算法对2个测试函数的帕累托前沿(Pareto frontier,PF)的比较中可以观察出,GTMOPSO能基本覆盖本文中2种测试函数的PF,且分布较PSO算法更均匀.

图4 PSO与GTMOPSO帕累托前沿对比Fig.4 Comparison of Pareto front between PSO and GTMOPSO
3.4 算法应用
根据以上分析,采用GTMOPSO算法对微电网系统优化配置模型进行求解,主要步骤如下:
1) 读入风速、辐照强度、温度及交直流负载数据,设定系统中氢储能以及蓄电池的初始荷电状态,并输入设备相关参数,编入第2节内容中所给出的包含氢储能和用户侧响应的微电网数学模型与约束条件,以及设置的微电网系统混合储能侧协调控制策略.
2) 初始化1组待优化变量,并随机生成粒子的位置与速度,其中每个粒子代表1组解.将粒子值代入公式(13)和(14)中,计算微电网系统经济性指标与换流损耗值指标,获得各个目标的适应度值,更新个体最优解与全局最优解.
3) 进行粒子非占优排序和拥挤距离分层选取,选择2个精英粒子a和b与非精英粒子x进行博弈,将博弈成功粒子以及博弈失败进行重新学习的粒子替换原种群中的非精英粒子,完成新精英粒子集的重构.
4) 通过混沌更新公式(25)对全局最优解进行混沌搜索,比较混沌搜索粒子与原粒子的支配关系,确定并更新系统全局最优解.
5) 利用公式(26)与(27)更新粒子的速度与位置,判断是否达到中止条件,满足则输出目标函数及待优化变量值,否则返回步骤(3).
具体求解流程见图5所示:
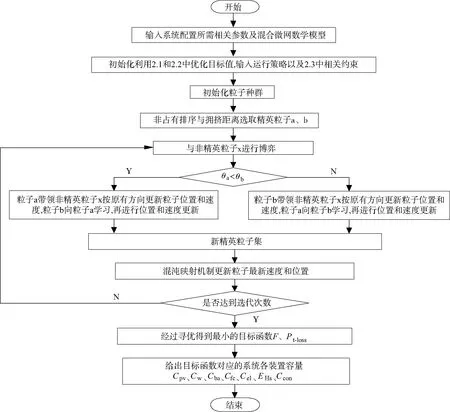
图5 算法流程图Fig.5 Algorithm flow chart
4 算例分析
4.1 仿真场景
根据本文搭建的数学模型,微网系统部分参数及分时电价数据见表2和表3.表4为引入的分时电价弹性矩阵中各自弹性系数和互弹性系数取值.选取某地区的风光数据和交直流负载数据作为系统输入数据,仿真步长为 1 h,全年 8 760 h,全年平均光照强度和风速分别为 166 W/m2、6.12 m/s,平均交直流负荷量分别为 128.037 9 kW/h 和 182.911 3 kW/h,具体数据如图6所示.

表2 不同设备的成本参数
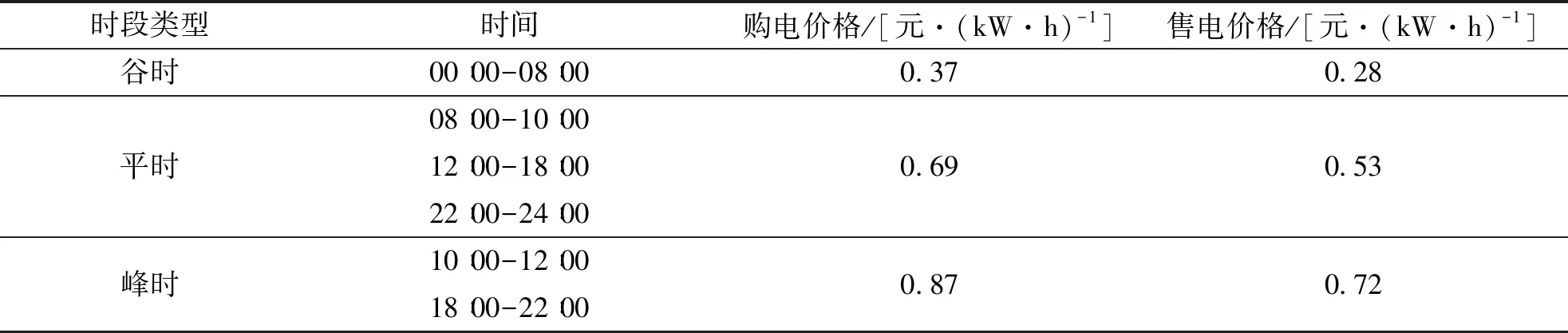
表3 分时电价

表4 分时电价弹性矩阵各系数值
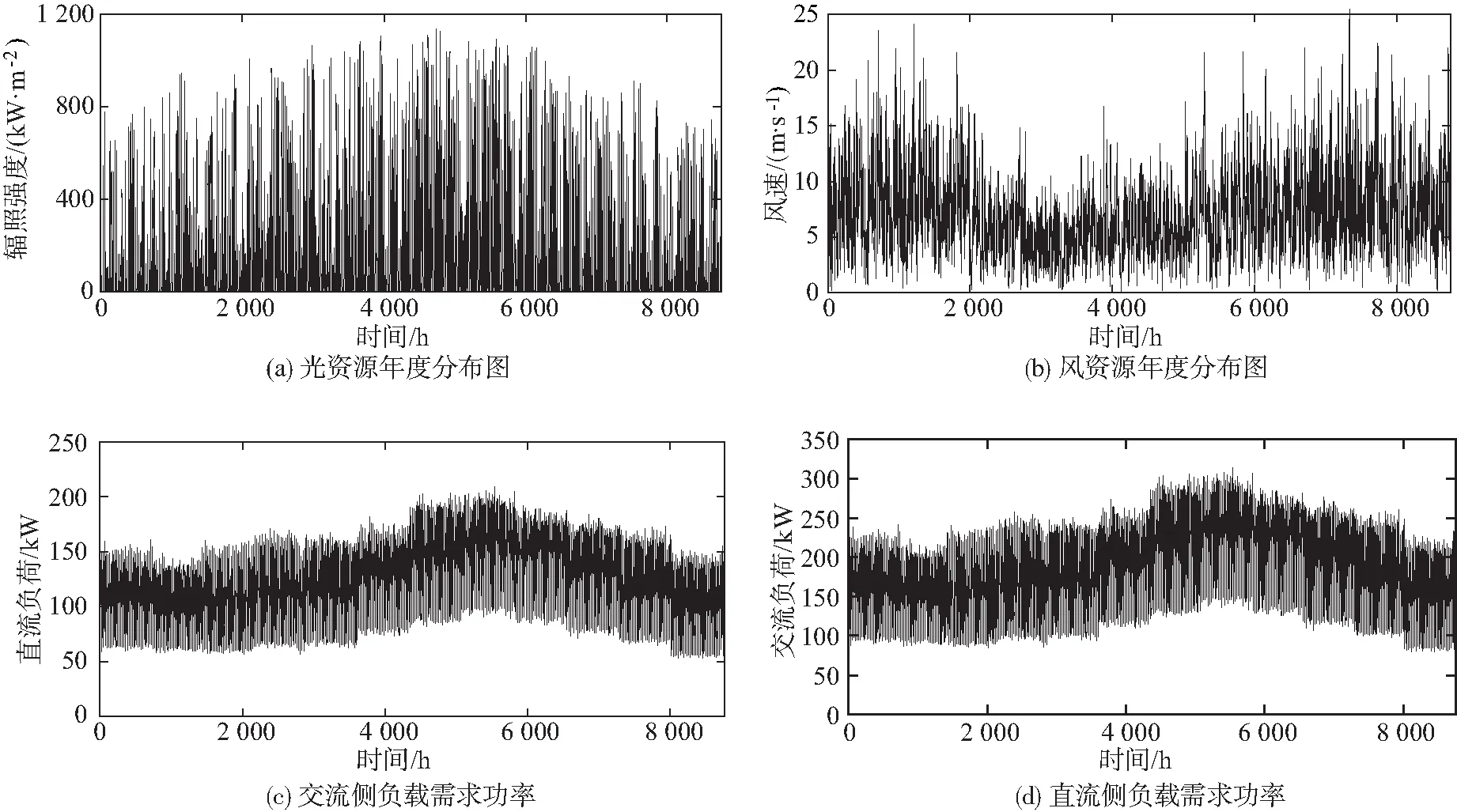
图6 年度风、光及交直流负载数据Fig.6 Annual wind, sunlight and AC-DC load data
4.2 仿真结果及分析
根据本文所提容量优化配置方法,设置粒子种群数量为30,迭代次数为100,同时与标准PSO算法得出的优化结果作为对比,根据是否实施基于弹性矩阵M的分时电价得到4种配置方案,具体配置方案如下:
方案1:不引入分时电价弹性矩阵,利用PSO算法对目标函数和待优化变量进行求解;
方案2:引入分时电价弹性矩阵,利用PSO算法对目标函数和待优化变量进行求解;
方案3:不引入分时电价弹性矩阵,利用GTMOPSO算法对目标函数和待优化变量进行求解;
方案4:引入分时电价弹性矩阵,利用GTMOPSO算法对目标函数和待优化变量进行求解.
根据4种方案对目标函数和优化变量进行求解,得到结果如表5所示.

表5 优化配置结果和目标函数值
由表5可得,2种优化算法在不同场景下均能得到最优的配置方案,对比方案1、2和方案3、4可以看出,GTMOPSO优化算法得出的微网等年值成本F和换流损耗Pt-loss相较于PSO算法在考虑非分时电价机制和分时电价机制下分别降低了2.67万元、0.77 MW 及3.21万元、0.79 MW;对比方案1、3和方案2、4可以看出,方案2、4由于分时电价机制的引入,有效降低了分布式电源和储能装置源的总容量,但随着其他成本的增加,微电网等年值成本相差不大,引入分时电价弹性机制后,2种不同优化算法得出的经济性优化目标值相较于未引入本文所提基于用户侧机制分别降低了2.07万元和1.54万元.交直流混合微网中基于分时电价弹性矩阵机制的引入,使得交直流用户用电行为更贴近交直流子网分布式电源的出力情况,并有效降低了风机、光伏以及储能装置的总装机容量,通过交直流子网自发自用,交直流母线间的等年换流损耗值也得到明显的降低.对比表5可以看出,2种优化算法得出的换流损耗值分别降低了 5.63 MW 和 5.62 MW.
5 结 论
对微电网的容量进行优化配置可以对风光资源进行合理利用,降低风光资源的浪费,进一步提高微电网系统的经济性.通过4种不同的方案进行仿真,可得到以下结论:
1) 对交直流混合微网进行自发自用,可有效降低交直流母线间的换流损耗值,在交流母线和直流母线两侧的负荷量分别引入分时电价弹性矩阵后,可通过影响用户侧的负荷结构,使得交直流负荷值与风机和光伏系统输出功率值更吻合,进一步减少微电网中各微源的配置容量,降低微电网的投入成本和运行成本,提高微电网系统的经济性和可靠性.随着微电网成本的降低,更有利于可再生能源的渗透.
2) PSO和GTMOPSO优化算法都能得到相应目标函数下微电网容量配置的最优方案,但通过仿真实验可以得出,改进后的寻优方案较改进前得到的寻优效果更好,所得配置方案目标函数更优.

