一类奇摄动分数阶微分方程的渐近解
李金洲,包立平
(杭州电子科技大学理学院,浙江 杭州 310018)
0 引 言
近些年来,分数阶微分方程不仅在热传导[1]、粘弹性力学[2]等物理学问题上应用广泛,而且在初值问题[3]、边值问题[4-5]、稳定性理论[6]等分数阶微分方程理论方面取得了重大进展。奇摄动分析作为解决理论和应用问题的重要工具,在研究分数阶微分方程边值问题方面起到重要作用。文献[7-8]用微分不等式方法得到了奇摄动分数阶微分方程边值问题的一系列结果。本文讨论一类奇摄动分数阶线性微分方程边值问题,运用双参数展开法得到解的高阶形式展开以及边界层矫正项,并运用极值原理[9]进行余项估计。
1 奇摄动问题外部解
一类分数阶奇摄动微分方程边值问题如下:
(1)
y(0)=α,y(1)=β
(2)

(3)

(1)a(x)在区间[0,1]连续,且对于任意x∈[0,1],a(x)≥m>0,m与ε无关;
(2)b(x)在区间[0,1]连续,且对于任意x∈[0,1],b(x)>0。
构造原边值问题(1)—(2)的外部解展开式为Y(x,ε,μ),令
(4)

再进行ε和μ双参数展开,令等式两端ε和μ同次方幂系数相等,可得:
(5)
Yn,m(0)=0n>0或m>0
(6)


(7)

退化解Y0,0的微分方程式为:
(8)
Y0,0(0)=α
(9)
由式(8)—式(9)得到Volterra积分方程:
(10)
2 边界层矫正项
由奇异摄动理论构造x=1点处的内解,设边值问题(1)—问题(2)的解为:
y(x)~Y(x,ε,μ)+Z(τ,ε,μ)
(11)
(12)

H1(x)=Zn,m(x)-Zn,m(0)

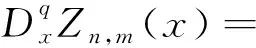

(13)



(14)
将式(4)、式(11)—(14)代入式(1),得到:
(15)
Z0,0(0)=β
(16)
Zn,m(0)=0n>0或m>0
(17)
Zn,m(∞)=0
(18)
式中,Wn,m(τ)为由Z0,0(τ),…,Zn,m-1(τ),…,Zn-1,m(τ)决定的已知函数,当n=m=0时,W0,0(τ)=0。将式(15)进行q阶积分,得到:
(19)
式中,C1为任意常数。结合定解条件(16),对分数阶微分方程(19)求解,得到:
(20)
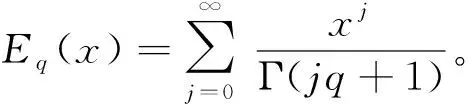
将式(18)代入式(20),得到C1=0,由此可得:
(21)
为了使内解存在,令Wn,m满足如下条件
(22)
当n或m>0时,将式(15)两边进行q阶积分后再p次迭代,得到
(23)


(24)
3 余项估计
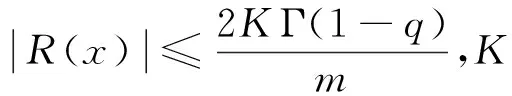
证明将解y(x,ε,μ)=Y(x,ε,μ)+Z(x,ε,μ)+R(x)εN+1μM+1代入式(1)、式(2),得到
(25)
由形式渐近展开式构造,可得:
(26)
R(0)=0,R(1)=0
(27)

(28)
(29)
结合式(26)、式(28)、式(29)可以得到:
(30)

(31)

(32)

4 结束语


