基于HHT变换和近似熵的管道泄漏检测方法

钟 华，邢懿鹏，丁颖铖，赵荣华

(杭州电子科技大学通信工程学院，浙江 杭州 310018)

0 引 言

目前，我国供水系统中，较长的服役期、逐渐腐蚀的介质和老化的材料使得城市供水管道泄漏成为了不可避免的问题，及时发现管道泄漏不仅可以避免安全事故的发生，还可以降低因漏水导致的财产损失[1]。管道泄漏检测技术的研究已取得不少成果。文献[2]运用相关分析法对管道漏点定位技术展开研究，通过分析水管首、末端采集信号的互相关程度实现了供水管道的泄漏检测及定位，但检测结果受噪声影响较大。文献[3-4]在经验模态分解(Empirical Mode Decomposition, EMD)的基础上，提取能量特征，提高了高信噪比时的管道漏点定位准确度，但低信噪比时的定位效果差。针对管道泄漏信号的非平稳特性，文献[5]通过设置频率幅值阈值的方法，根据泄漏信号集中频段和频率幅值特征进行泄漏检测，但检测性能受初始阈值影响较大；文献[6]采用EMD和小波包相结合的处理方法，解决了低信噪比时泄漏信号去噪难的问题，但小波包的分解效果受小波基的选择影响较大。

希尔伯特黄变换(Hilbert-Huang Transform，HHT)分为EMD分解和Hilbert变换两部分。对非线性信号进行EMD分解就是将其转换为线性信号，这种方法也适用于非平稳信号的平稳化，并保留了信号的本身特性[7]。EMD分解无需选择基函数就可把复杂信号按照频率由高到低依次分解为若干本征模态分量(Intrinsic Mode Function, IMF)和1个残余分量。Hilbert变换从根本上突破了传统傅里叶变换理论的限制，观察Hilbert时频谱和边际谱信号的幅频分布情况有助于深入分析信号的本质，特别适合处理非平稳信号，如泄漏信号。

1991年，为了衡量时间序列的复杂程度，Pincus[8]提出了近似熵，用于度量振动信号中产生新模式的概率。通过对比近似熵可以区分HHT提取出的泄漏信号和噪声信号，从而实现泄漏信号的检测。本文提出一种基于HHT和近似熵相结合的水管泄漏检测方法。

1 泄漏信号模型

水管泄漏时，管内外存在压力差，于是产生不同频率的振荡信号。裂开的管道和包裹管道的土壤等介质和管内喷出的高压水发生不同程度的摩擦，产生频率不同的振荡信号，水管泄漏信号的模型如图1所示。此外，复杂的采集环境中，采集器还会随机获取干扰噪声信号，所以，采集信号是泄漏信号与噪声信号的组合，属于非平稳随机信号，采集信号模型表示如下：

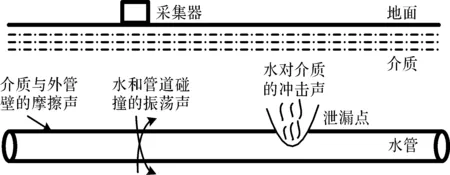
图1 水管泄漏信号模型

(1)

式中，ai和wi分别表示第i个振幅和振荡频率，r表示泄漏点到采集器的距离，v表示泄漏信号在管道中的传播速度，n表示频率成分的个数，n(t)表示随机干扰噪声。

2 泄漏检测原理

本文提出的泄漏检测方法包括HHT和近似熵求解。由于时域信号包含有效信息较少，所以，先对采集信号进行HHT，得到信号的Hilbert边际谱，并在频域将泄漏信号和噪声区分开来；再以泄漏信号的Hilbert边际谱为输入对象，求出特定频段内的近似熵，以此作为判决对象，构建定量的泄漏检测标准。

2.1 希尔伯特黄变换

HHT分为EMD分解和Hilbert变换。

EMD分解就是通过特征时间尺度获得若干IMF分量和1个残余项，再由IMF分量分解时间序列数据[6]。EMD分解的实现过程如下：

(1)将极大值点和极小值点通过三次样条函数依次连接，记m1(t)为x(t)的上下包络线平均值，分离出m1(t)后的原始信号h1(t)为：

h1(t)=x(t)-m1(t)

(2)

假设经过k次分离处理后的h1k(t)满足IMF的基本条件，即由数据序列的局部极值点确定的上下包络线平均值为0，则得到第1个IMF分量c1(t)=h1k(t)[9]。

(2)把c1(t)从信号x(t)中分离出来，得到r1(t)作为新的原始数据，依次重复以上过程，直到分离出所有满足式(1)中IMF的基本条件的IMF分量，原始信号x(t)便可以表示为这些IMF分量和1个无法分解的残余项rn(t)的组合：

(3)

式中，记IMF的分解次数为s；按由高到低的顺序记不同频段中的IMF分量为c1(t)，c2(t)，…，cn(t)；能够反映信号的整体变化趋势的残余项记为rn(t)。

爆品影响力可从两个维度进行判断：从用户层面，爆品具有话题感，渗透力和极佳的口碑；从行业层面，爆品具有标杆意义，能够形成现象级案例，像“芸保凯”一样在培训中、在制定企业战略时被广泛引用。

x(t)的另一种表现形式可以通过构造解析函数得到，即对每个IMF分量作Hilbert变换[7]，得到：

(4)

式中，ai(t)表示构造所得解析函数的幅度，φi(t)表示构造所得解析函数的相位，j表示复数的虚数单位。其频谱通常用H(w,t)表示：

(5)

在频域对解析函数做积分处理，得到Hilbert边际谱：

(6)

式中，T表示信号的持续时间。h(w)可以精确地表现信号的幅频变化规律，同时也表示全部统计数据长度的累加幅度，因而，Hilbert边际谱特别适合处理非平稳随机信号。

为了验证HHT对非平稳信号的处理效果，采用塑料管道系统进行实验，实验系统示意图如图2所示，实验环境如图3所示。将自来水通过快速接口引入管道的进水口，在距离进水口1 m处安置1个压力表测试进水水压，并以针孔阀代替泄漏点，通过调节其开度来设置泄漏情况，分为小口泄漏、中口泄漏以及大口泄漏。用于采集振动信号的2个压电传感器分别置于泄漏点的两端距离泄漏点L1和L2的位置，进入管道的水从出水口处通过水龙头放出。管道外部不包裹任何介质，周围背景噪声已提前采取。实验参数设置如表1所示。

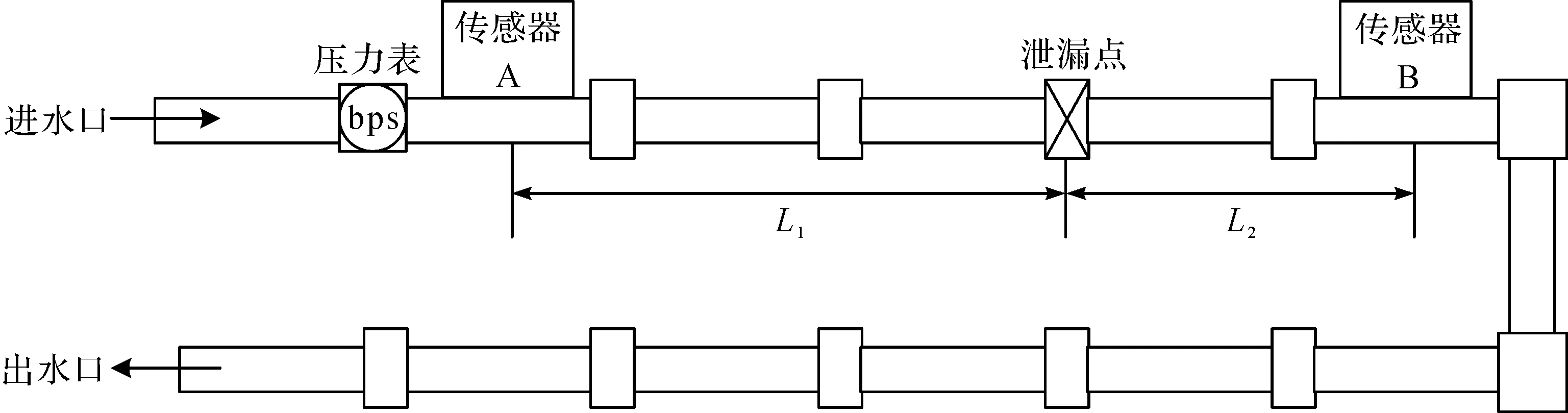
图2 管道系统的示意图

图3 实验环境实拍图

表1 管道系统实验参数

选用采集到的一组小口泄漏信号进行仿真，得到的噪声信号和泄漏信号的功率谱图如图4所示。从图4可以看出，噪声信号的功率谱和泄漏信号的功率谱在形状上存在一定的相似性且没有明显的规律性，较难直接根据功率谱将干扰噪声信号和泄漏信号区分开来。

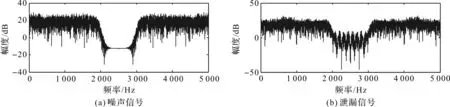
图4 噪声信号和泄漏信号的功率谱图

经EMD分解后的泄漏信号IMF分量如图5所示，其中残余分量较小，忽略不计，前4个IMF分量的功率谱图如图6所示。从图6可以看出，IMF分量由高频到低频依次分布，体现了EMD分解的特点，其中IMF1分量主要为噪声信号，而泄漏信号主要分布在IMF2分量上。采集信号经过Hilbert变换后得到的边际谱图如图7所示。

图5 经EMD分解后的泄漏信号IMF分量

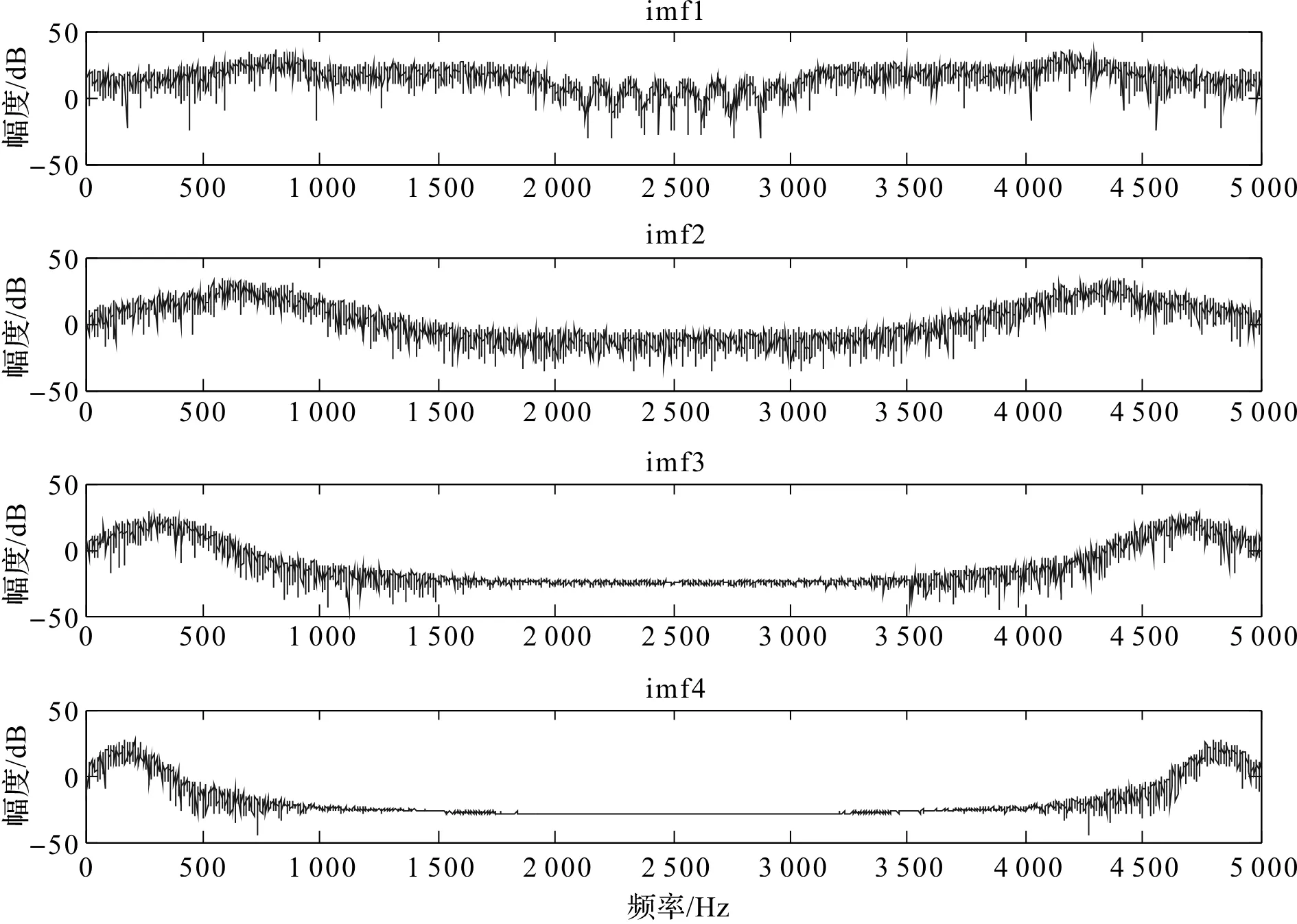
图6 IMF1～IMF4分量的功率谱

图7 采集信号的Hilbert边际谱

2.2 近似熵计算

为了区分噪声信号和泄漏信号，需要对Hilbert边际谱作进一步的定量处理，本文采用近似熵方法对有效频段内(600～1 000 Hz)的边际谱求解近似熵，作为最终的检测标准。近似熵作为一种时间序列的度量方法，可以表征信号的复杂性和规律性。随着维数的改变，序列相应的近似熵和其复杂程度成正比[8]。给定长度为N的一维序列{u(p),p=1,2,…,N}，该序列的近似熵求解过程如下。

(1)根据原始序列u(p)重构m维向量，即

Xp={u(p),u(p+1),…,u(p+m-1)},p=1,2,…,N-m+1

(7)

(2)计算任意向量Xp与其余向量Xq(q=1,2,…,N-m+1,q≠p)之间的距离：

dpq=max|u(p+q)-u(q+k)|,k=0,1,…,m-1

(8)

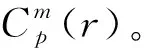
(9)

(5)将m增加1，重复以上步骤得到φm+1(r)，从而求出近似熵A为：

(10)

本文提出的基于HHT和近似熵相结合的供水管道泄漏检测方法的流程如图8所示。

图8 供水管道泄漏检测方法流程图

3 实验结果与分析

为了保证实验数据的真实性与可靠性，本文通过塑料管道实验系统进行模拟实验。对实验中采集到的多组泄漏信号进行仿真实验。首先对3种泄漏情况下的声信号进行时频分析，信号在不同泄漏情况下的功率谱图如图9所示。

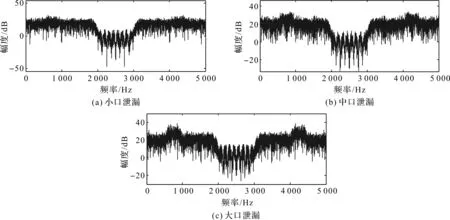
图9 不同泄漏情况下的信号功率谱图

从图9可以看出，管道背景噪声的频率成分充满整个频带，而不是集中在某段频带内；在大口泄漏情况下，由于信噪比较大，有效泄漏信号较为明显，在低频600～1 000 Hz内出现谱峰，这主要是由管内高压水在管内流动时引起的管道振动产生的；小口泄漏和中口泄漏情况下，由于信噪比较小，有效泄漏信号基本无法辨别，很难直接根据信号的功率谱来区分噪声信号和有效泄漏信号。

分别采取3种泄漏信号以及噪声信号各20组样本，计算其Hilbert边际谱在有效频段内的近似熵，结果如图10所示。

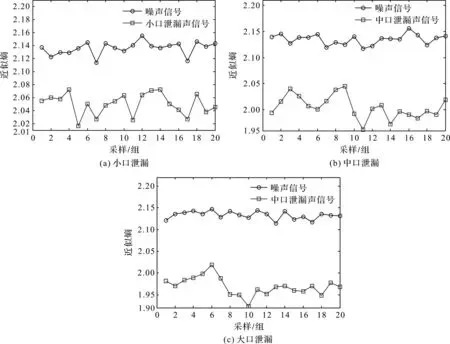
图10 3种泄漏信号Hilbert边际谱的近似熵

从图10可以看出，噪声信号边际谱的近似熵始终保持在2.11～2.16之间，而3种泄漏信号边际谱的近似熵分别保持在2.02～2.07，1.97～2.05，1.92～2.02之间，均小于噪声信号的近似熵，表明泄漏信号边际谱的能量更加集中。此外，噪声信号的近似熵最小值为2.11，而泄漏信号的近似熵最大值为2.07，小于噪声信号的近似熵最小值。所以，可以将近似熵数值的大小作为区分噪声信号和泄漏信号的标准。

取实验采集到的噪声信号以及3种泄漏信号各120组，分别采用文献[5]的频率幅值法和本文提出的基于HHT与近似熵的管道泄漏检测方法处理噪声信号和3组泄漏信号，结果如表2所示。

表2 不同检测方法的检测结果比较

从表2可以看出，本文方法的检测准确率达到了95%以上，文献[5]方法的中小口泄漏信号检测准确率明显低于本文方法。

4 结束语

本文通过分析采集信号的频域特征，引入近似熵作为泄漏检测的判决对象，提出一种基于HHT与近似熵的管道泄漏检测方法。实验结果表明，相比于传统的频域检漏方法，基于HHT与近似熵的管道泄漏检测方法具有更高的检测准确率，为其他类型的管道泄漏检测提供了新的研究思路。如何将本文研究的结果应用于泄漏点定位和泄漏等级分类中是下一步研究的重点。