立足本质 多元化说理

文|林荧荧

构建小学数学说理课堂是学生深度学习的有效策略，它体现了当代前沿的教育教学理念，是站在儿童立场的教学。数学说理能让课堂回归育人的原点，促进教师对教材的本位解读，促进儿童思考力、表达理解力的培养。在教学中怎样践行说理呢？下面，笔者结合《2、5 的倍数特征》这一节课，谈谈在备课、研课、上课中的所思所悟。

一、多版本对比，求同知异，深研教材

《2、5 的倍数特征》是一节看似简单却富有探究空间的课。对于五年级的学生来说一般都能通过观察，自主发现与陈述2、5 的倍数特征。人教版、苏教版和北师大版的教材都采用了百数表，让学生先按要求进行圈数、框数，然后在观察比较中自主探究2、5 的倍数特征，接着在反馈交流中总结明晰规律，最后三个版本教材都是通过对话的形式，呈现和完善2、5 的倍数特征。按照教材的呈现方式，教师常见的教学方式是依托教材呈现的百数表组织学生探究总结出2、5的倍数特征，最后根据特征判断一个数是否是2、5 的倍数。这样的教学直击“掌握2、5 的倍数特征”的目标，却少了对“2、5 的倍数特征”的理性思考。

在三个版本的教材中，只有人教版的教材在本单元末“你知道吗”中对2、5 的倍数特征的原理以算式表达的形式加以介绍，如：

24=20+（ ）

2485=2480+（ ）

因为20、2480 都是2 或5 的倍数，所以一个数是不是2 或5 的倍数，只需要看个位数。

这样的拓展阅读能启发学生的思考，特别是那些善于动脑、喜欢寻根究底的学生。但是小学生是以形象思维为主，这种算式表达式的呈现方式是比较抽象的，对于一般的学生来说，还是比较难以理解的。

带着对教材的研究，再来研读台湾康轩版的教材，台湾版教材将2、5、10 的倍数特征整合成一节课，教材设计了一个数字机器的游戏，激发学生探究的兴趣，然后让学生先找出符合要求的数，再通过观察，发现其中的规律。最后在“做做看”中，基于2、5 倍数的特征，判断哪些数是2、5 的倍数。

对比四个版本的教材，引发深度思考：2、5 的倍数的教学是不是就止步于对特征的探究呢？五年级的学生，在本节课教学前基本上已经知道了2、5 的倍数特征了，那基于学情，本节课新的“生长点”又会是什么呢？带着思考，继续研读台湾版教材《3 的倍数特征》，台湾版教材对“3 的倍数特征”的探究，更注重以数形结合的形式，让学生在分方块中明白每个数位上的数就刚好是3 个分一堆后剩下的数，从而引发学生思考，悟到“为什么3 的倍数只要看各数位上的数的和”的道理。

多种表征，数形结合，直击本质，这样的课堂是不是更有“深度”呢？以《3 的倍数特征》为鉴，我们《2、5的倍数特征》的教学又有哪些地方可借鉴的呢？一节简单的《2、5 的倍数特征》，怎样才能把它上得更厚，更有“数学味”呢？基于学生素养的发展，《2、5 的倍数特征》的教学，不应只停留在“特征认识”的教学上，而应提高到“特征原理”的探究上，不仅要让学生知其然，而且要知其所以然。

二、多元化析理，立足本质，重构课堂

1.以形明理，显直观。

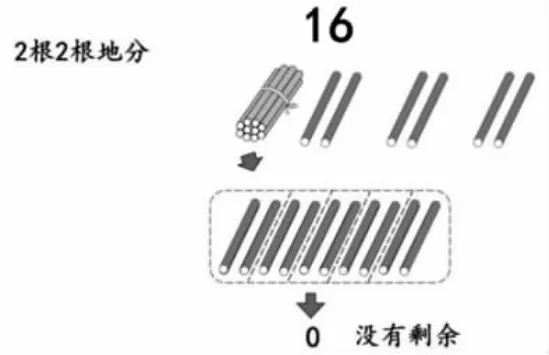
“数缺形时少直观，形少数时难入微。”小学生以形象思维为主，所以教师可以通过分小棒、分方块，让学生直观看到分的过程，让学生明确：十位上的数不管是几，2 根2 根或5 根5 根地分都是没有余数的，也就是说不管是几十都能整除2 和5，所以只要看个位上的数就可以了。以此类推到三位数：如126，百位上的1 表示100，2 个2 个地分是没有余数的；十位上的2，表示20，2 个2 个地分也是没有余数的，所以也是只看个位上的数就可以了。通过借助小棒或方块的“形”，达到阐述“数理”的效果，直观地让全体学生都领悟到其中的道理。

2.拆数释理，见本质。

如果说“以形释数”画图比较麻烦，也可以利用拆数法，举例来说理，可以有以下两种拆数的方法，方法虽然不同，但殊途同归。

（1）根据位值制拆成“几百”加“几十”加“几”。

如54=50+4，50 是10 的倍数，10 的倍数就一定是2 或5 的倍数，所以只要看个位4 是不是2 或5 的倍数，因为4 是2 的倍数，不是5 的倍数，所以54 是2 的倍数，不是5 的倍数。

又如125=100+20+5，100 是10 的倍数，就一定也是2 或5 的倍数；20 也是10 的倍数，也一定是2、5的倍数；所以看个位，5 是5 的倍数，但不是2 的倍数，所以125 是5 的倍数，不是2 的倍数。

（2）拆成“10 的倍数”加“个位数”。

把125 拆成120+5，因为120 是10 的倍数，一定是2、5 的倍数，所以判断125 是不是2、5 的倍数只要看个位就可以了。

通过拆数可以发现所有非0 的自然数都可以拆成“10 的倍数”加“个位数”的形式，其中10 的倍数部分一定是2、5 的倍数，所以只要看余下的个位是否是2 或5 的倍数，就可以判断是否是2 或5 的倍数。

3.演绎推理，巧建构。

举例验证是不完全归纳法，如果觉得举例不够严谨，还可以用代数式的方法证明结论。

可以假设这个数为P（P 为整数），当P 是两位数时，P=10b+a（a、b 为整数）。因为10b=5×2×b，所以10b是5 或2 的倍数，只要个位a 是5 或2 的倍数，那么10b+a 就是5 或2 的倍数，P 就是5 或2 的倍数。

当P 是三位数时，P=100c+10b+a=（10c+b）×10+a；（10c+b）×10 是10 的倍数，一定也是5 或2 的倍数，所以只要看个位a 是否是5 或2 的倍数，就可以判断P 是否是5 或2 的倍数。

同理，当P 是四位数时，P=1000d+100c+10b+a=（100d+10c+b）×10+a；（100d+10c+b）×10 是10 的倍数，也就是5 或2 的倍数，所以只要看个位a 是否是5 或2 的倍数，就可以判断P 是否是5 或2 的倍数。

三、基于本质延伸，适时拓展，丰实教学

《2、5 的倍数特征》这节课的教学基于学科本质，教师的教学不仅可以“深”下去，还可以“远”开来。如在最后出现表示位值制的字母表达式后，教师可以再抛出延伸性的问题：看到这个式子，你还有什么启发？你还能想到什么？想想看，用这样的方法还能发现其他数的倍数特征吗？比如4 的倍数特征。

感兴趣的学生课后还可以继续深挖，如果是6的倍数、8 的倍数或是其他数的倍数又会是怎样的结果呢？

从“是什么”到“为什么”，再到“还可以是什么”，教师把重点放在对“为什么”的探究上时，其实就为学生洞察现象背后的本质提供了“真探究”的契机，这样的学习是有深度的，可以延伸出后续的更多精彩，这样的教学厚度更丰实。

总之，数学是讲道理的，理越辩越明。教师应让学生学会“讲道理”，以“核心问题”为驱动，引领学生质疑、讲道理，通过多样化数学工具，让学生进行数学表达，提升学生的数学理性精神，培养数学素养。