输流管道弯曲和振动的有限元分析*

随岁寒 李成

(1. 商丘工学院 机械工程学院， 商丘 476000)(2. 常州工学院 汽车工程学院，常州 213032)(3. 暨南大学 “重大工程灾害与控制”教育部重点实验室， 广州 510632)

引言

输流管道广泛应用于石油化工、航空航天和海洋工程等领域，对其弯曲和振动特性进行研究能够为工程设计、结构优化和应用提供重要参考.输流管道力学问题的研究涉及流体力学、固体力学、动力学与控制等多个学科，已有大量文献研究输流管道的流固耦合振动特性[1-22]，这些工作主要聚焦在输流管道的动力学响应及稳定性，大部分为宏观输流管道，也涉及微观情形，如输流碳纳米管[5,7].然而，以往对输流管道在外力作用下的弯曲变形问题研究不多.Dai和Wang[4]基于Euler梁模型给出了输流管道的弯曲及振动的控制方程，应用有限元法对控制方程进行求解，其中考虑管道受到集中磁铁引力载荷.为分析管道弯曲问题，本文利用加速度合成定理推导了流体横向加速度的表达式，具体包括三项，即牵连加速度、科氏加速度和向心加速度，具有明确的物理意义.这与2019年田耀宗和蹇开林根据速度场概念推得的形式一致[23]，但途径不同.随后本文基于Timoshenko梁模型推导了重力作用下水平布置输流管道弯曲问题的有限元格式，分析了两端简支和悬臂两种边界条件下流体流速对管道挠度和转角的影响.此外，在两端简支边界条件下还考虑了预应力的因素.

另外，以往应用有限元法研究输流管道流固耦合振动问题的文献相对较少[1-4].梁波等[2]基于Timoshenko梁模型，根据Hamilton原理推导出了输流管道系统动力学有限元方程，分析了输流管道的动力特性与稳态响应.王世忠等[3]基于Euler梁模型建立了输流管道流固耦合振动的有限元方程，分别讨论了流速、压强变化等因素对管道固有频率的影响.与其不同的是，本文利用虚功原理推导了输流管道系统动力学的有限元方程，考虑到管道在热胀冷缩以及安装等外界条件下承受的轴向预应力，因此动力学方程中计入了预应力因素.此外，与以往研究专门将预应力单列，分析预应力做功不同，本文将预应力作用效应直接体现在总的应变能中.

本文主要框架如下：首先，基于虚功原理建立了输流管道系统的有限元方程；其次，分析了两端简支和悬臂两种边界条件下管道受重力作用时的弯曲以及流速对结果的影响，研究了两端简支边界条件下管道预应力与挠度间的关系；最后，分析了两端简支和悬臂边界条件下管道的自由振动与流速的关系，讨论了在两端简支边界条件下管道预应力与系统固有频率间的关系.

1 物理模型

为建立输流管道流固耦合振动的有限元方程，对输流管道建立如图1所示的坐标系，输流管道在两支撑间的距离为L，受到轴向预应力σ0，管道内径r1，外径r2.

图1 输流管道示意图

根据Timoshenko梁理论，梁的位移场可表达为

u(x,z,t)=-zψ(x,t)

w(x,z,t)=w(x,t)

(1)

其中，u(x,z,t)和w(x,z,t)分别是轴向位移和横向位移，ψ为转角，t为时间.正应变εxx及切应力γxz可表达为[24]

(2)

对于各向同性弹性材料，应力在虚应变上所做虚功为

(3)

如图2所示建立管道微段动坐标系O′x′y′，流体横向加速度可由点的加速度合成定理得到

图2 流体加速度分析

aa=ae+ar+aC

(4)

牵连加速度大小为

(5)

微管段中性面斜率、中性面旋转角速度分别为

(6)

(7)

从而科氏加速度大小为

(8)

管道曲率为

(9)

(10)

考虑流体向心加速度方向后得到

(11)

将式(5)、式(8)和式(11)代入式(4)，得到流体横向加速度大小为

(12)

与按照场概念计算结果相同[23].

管道和流体的惯性力虚功为

(13)

其中，A1代表流体截面，A2代表管道截面.

外力虚功为

(14)

其中，g为重力加速度并假设其方向沿y轴正方向.

将式(3)、式(13)和式(14)代入如下虚功原理表达式

δU+δWin=δWE

(15)

并略去应变能高阶项得到

6）加强库内通风换气。经常检查，一旦发现虎皮病有发生苗头，立即组织出库销售，杜绝病害蔓延，避免整库果实染病，造成重大损失。

(16)

采用如下形函数

(17)

其中

将式(17)代入式(16)得到输流管道系统有限元方程

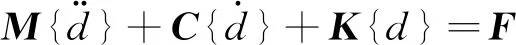
(18)

其中，质量矩阵M、陀螺矩阵C、刚度矩阵K和外力矩阵F分别为

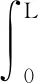
(19)

2 数值算例

设管道长度L=8 m，弹性模量E=210 GPa，泊松比为0.3，密度7850 kg/m3；管外壁半径r2=0.1885 m，内壁半径r1=0.1825 m；流体密度为800 kg/m3.

2.1 管道弯曲分析

在分析管道在自重下的弯曲时，将式(18)中与时间相关的项略去，对悬臂管道还须令预应力σ0=0，得到如下静力学方程

K{d}=F

(20)

其中，刚度矩阵K与无流体管道对比，增加项代表的是管道受到的流体离心力，即式(11).求解式(20)可得管道横向位移和转角.

两端简支边界条件下，管道受重力而产生y正方向的挠度，流体离心力总是垂直于管道且和重力方向相同，因此流体速度越大，管道的挠度和转角越大.图3和图4分别为两端简支管道的挠度和转角，其与流体速度的关系符合理论预测.图5给出了流体速度v=80 m/s的条件下轴向预应力的变化对两端简支管道的挠度的影响，可见预应力越大则挠度越小，预应力的存在有效增强了输流管的抗弯刚度.

图3 两端简支管道的挠度(σ0=0)

图4 两端简支管道的转角(σ0=0)

图5 轴向预应力对两端简支管道的挠度的影响

在悬臂条件下，流体离心力总是和重力方向相反，因此随着流速的增大管道挠度和转角逐渐减小，图6和图7分别为悬臂管道的挠度和转角，其与流体速度的关系符合理论预测.

图6 悬臂管道的挠度

图7 悬臂管道的转角

2.2 管道自由振动分析

略去式(18)中外力矩阵，同样对悬臂管道须令预应力σ0=0，得到如下自由振动方程

(21)

求解式(21)得到管道系统各阶振动频率.文献[11]基于Euler梁理论，利用直接解法得到前三阶固有频率的解析解为

(22)

(23)

(24)

表1给出了简支管道流速为零时的前三阶固有频率与ANSYS所得结果的对比，误差在4%以内，证明本文分析方法有效.图8给出了两端简支管道系统前三阶固有频率与流速的关系，其中虚部代表固有频率，实部表征系统稳定性.当流体速度为220 m/s时，第一阶固有频率虚部为零，这一速度可称为临界速度，此时实部开始分岔提示系统失稳，这一失稳形式属于动态失稳，因为系统第一阶模态类似静态弯曲挠度(图3)，当流体速度超过临界速度时，过大的流体离心力将对管道造成破坏.本文得出的有限元结果与文献[11]的结果在速度改变时规律相同，即流体速度越大，各阶固有频率越小，且数值结果一致.表2给出了前三阶固有频率随管道预应力的改变规律，可见随着管道预应力的增大，前三阶固有频率均表现出增大趋势，在管道轴向预应力从-100 MPa到100 MPa的增大过程中，前三阶固有频率的增加幅度分别为29.46%、5.17%和2.22%.

表1 简支管道固有频率对比(v=0 m/s)

表2 简支管道预应力与固有频率的关系(v=100 m/s)

表3给出了悬臂管道流速为零时的前三阶固有频率与ANSYS所得结果的对比，误差也在4%以内.图9给出了悬臂管道系统前三阶固有频率与流速的关系，可见流体速度增大则各阶频率减小，这一规律与两端简支管道相同，不同在于悬臂支撑条件下各阶固有频率低于两端简支情况.值得一提的是，本文在弯曲部分只考虑重力和流体离心力，而在振动部分还考虑了惯性离心力和科氏力，因此流速的增大使得悬臂输流管道的变形和振动频率均降低.与图8两端简支的边界条件不同，即使流体速度大于临界速度，图9前三阶固有频率的实部都为负，这表示此时系统仍然稳定.针对这一现象，以第一阶模态为例说明如下：输流管道偏离平衡位置振动时，离心力和科氏力与恢复力方向相同，即阻止了振动的发生.第一阶固有频率为零意味着在这些流速数值下不产生第一阶模态振动，因此悬臂管道第一阶固有频率为零的状态可归为静态失稳.

(a)虚部

表3 悬臂管道固有频率对比(v=0 m/s)

(a)虚部

3 结论

根据Timoshenko梁模型并利用虚功原理建立了输流管道弯曲和振动的有限元方程.考虑重力带来的管道弯曲变形和管道预应力效应推导了应力在虚应变上所做虚功，利用加速度合成定理分析了流体的加速度.随后分别分析了两端简支和悬臂边界条件下流速对管道弯曲和振动的影响，在两端简支条件下可退化为基于Euler梁模型的前三阶固有频率的解析表达，并分析了预应力效应.研究总结如下：

(1)两端简支条件下，流速越大，挠度和转角越大，管道轴向预应力增大挠度减小.流速提高，则前三阶固有频率减小，管道轴向预应力增大使得前三阶固有频率增大.

(2)悬臂边界条件下，流速越大，挠度和转角越小；较高的流速使得前三阶固有频率降低.

(3)输流管道作为典型的含有科氏力、离心力的动力学系统，求解得到系统复频率，并从中揭示了系统的稳定性.