周期轴向力作用下旋转圆锥薄壳动力稳定性研究*

韩勤锴 秦朝烨 褚福磊

(清华大学 机械系，北京 100084)

引言

薄壁壳体结构在土木工程、机械工程和航空航天工程中有着广泛的应用.在载荷参数值和横向振动固有频率的特定组合下，壳体结构在面内周期力作用下可能发生不稳定的横向振动，导致参数失稳，危及结构安全.半个世纪以来，具有不同几何、边界条件和荷载类型的壳体结构参数失稳问题得到了广泛研究[1,2].

从研究对象看，现有研究[3-7]多数集中于圆柱壳，而对圆锥壳的参数失稳研究相对较少.基于Marguerre型动力方程，Ye[8]分析了扁锥薄壳在周期性横向和面内载荷作用下的非线性振动和动力失稳.Ng等[9]利用广义微分求积(GDQ)方法研究了边界条件对周期边缘载荷作用下截锥壳参数失稳的影响.Sofiyev[10-12]对复合材料层合锥壳的热致动力失稳和屈曲行为进行了一系列研究.近期，不少学者探索了由碳纳米管增强复合材料[13]、功能梯度材料[14]以及金属泡沫材料[15]制成的截锥壳非线性动力失稳问题.

上述研究并未考虑旋转效应.对于周期性轴向载荷作用下的旋转圆柱壳，Ng等[16]和Liew等[17]报道了旋转引起的科里奥利力和离心力对失稳区域有显著影响.Lam和Hua[18]指出，将研究从旋转圆柱壳扩展到旋转圆锥壳所需的分析量相当大.此外，圆锥壳是更为一般的壳体结构形式.因此，研究旋转对周期轴向载荷作用下旋转锥壳参数失稳的影响具有重要意义.

GDQ方法最早由Shu和Richards[19]提出，用于直接求解工程问题的控制方程.目前，GDQ方法已广泛应用于壳体结构的振动分析[20-22].本文将基于该方法建立旋转锥壳的振动模型.考虑旋转效应后，周期轴向载荷作用下薄壁锥壳结构的动力学问题属于一类具有参数激励的陀螺动力系统.由于Floquet乘数假设不满足陀螺系统，经典Bolotin方法不能用于此类系统的参数稳定性分析[23,24].需借助更为普适的Hill方法[25].

因此，本文拟开展周期轴向力作用下旋转圆锥薄壳动力稳定性研究.基于Donnell薄壳理论[26]推导旋转锥壳的动力学方程，采用GDQ法和Hill法分析系统在周期轴向载荷作用下的参数不稳定性.通过与文献结果的对比，验证分析模型的准确性.研究不同转速和边界条件时系统主参数稳定区的变化，讨论轴向力相对变化幅值以及几何设计参数(锥角、长径比和厚径比)对不稳定区的影响规律.

1 分析模型

1.1 周期轴向力

本文考虑各向同性的截断型圆锥薄壳，其弹性模量为E，密度为ρ，泊松比为υ.图1给出了以角速度Ω绕其对称轴旋转的圆锥薄壳的几何结构和坐标系.其中，α为锥角，L为轴向长度，h为厚度，a和b是锥壳两端的半径.锥壳的基准面取其厚度中面，其中正交坐标系(x-θ-z)是固定的，r=r(x)是任意坐标点(x,θ,z)的半径.旋转锥壳在经向x、周向θ和法向z方向上的变形分别由u,v,w定义.

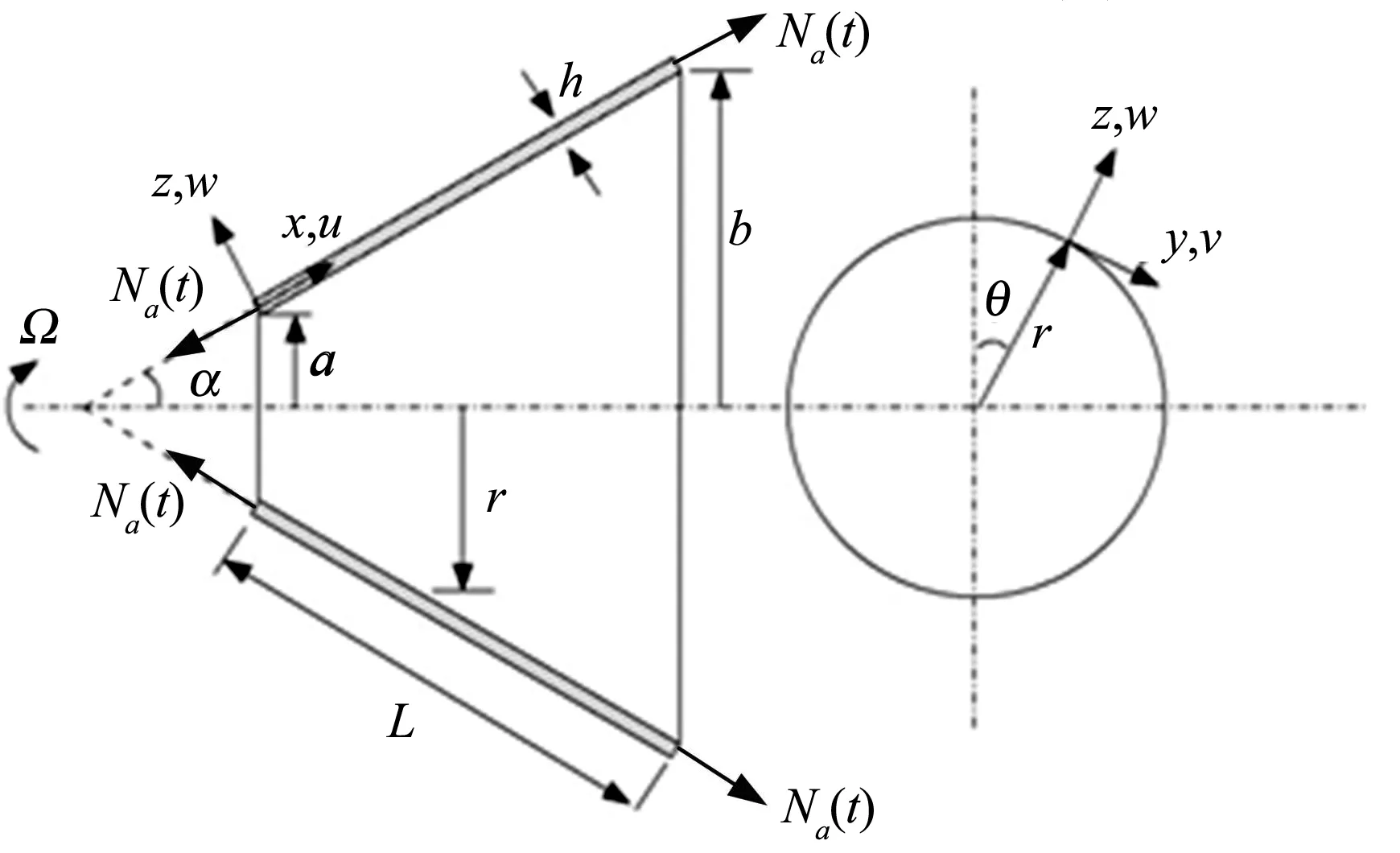
图1 旋转圆锥薄壳的几何结构和坐标系

旋转锥壳在图1所示的子午方向上承受周期性载荷Na(t)，其形式可假定为恒定载荷上叠加一个小正弦扰动量，即表示为如下形式

Na(t)=ηaNcr(1+εcosωat)

(1)

式中，ηa和ε分别表示恒定轴向力的幅值和相对变化幅值.Ncr表示当锥角α=0时的圆柱薄壳的屈曲载荷，有Ncr=Eh/[R(2(1-υ2)]1/2，其中R表示柱壳的半径.本研究中，令R=a.

1.2 旋转薄壁锥壳振动模型

根据Donnell薄壳理论[26]，图1所示的旋转圆锥壳体结构的动力学方程可表示为

(L+LT+LI+LN)u=0

(2)

式中，u=[u,v,w]T.L表示非旋转锥壳的微分算子矩阵，可参考文献[18].LT表示初始环向张力引起的微分算子矩阵，可表示为

(3)

式中

(4a)

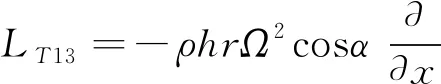
(4b)

(4c)

(4d)

(4e)

(4f)

式中，r=a+xsinα.LI表示惯性力微分算子矩阵，可表示为

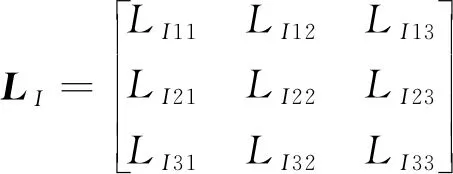
(5)

式中

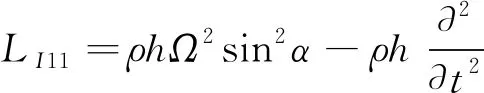
(6a)

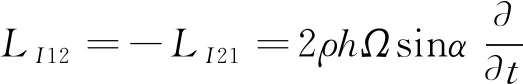
(6b)

LI13=LI31=ρhΩ2sinαcosα

(6c)

(6d)

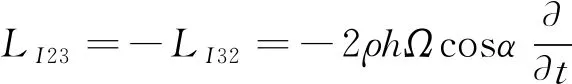
(6e)

(6f)

LN表示轴向力微分算子矩阵，可表示为

(7)

其中

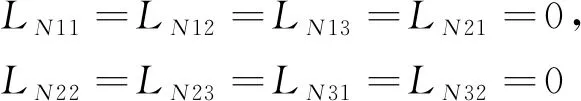
(8a)

(8b)

后续分析中，将考虑四种边界条件：小端固支和大端固支(Cs-Cl)、小端简支和大端固支(Ss-Cl)、小端固支和大端简支(Cs-Sl)以及小端简支和大端简支(Ss-Sl).

1.3 基于GDQ方法的离散模型

在应用GDQ方法之前，需确定圆锥薄壳自由振动的位移场为

(9)

L*u*=0

(10)

其中，u*=[U(x),V(x),W(x)]T是未知的振型空间函数向量，L*是维度为3×3的微分算子矩阵.GDQ方法的思路[19]：一个足够光滑的函数在一个离散点上相对于坐标方向的导数可以近似地表示为所有离散点上函数值的加权线性和.以函数U(x)为例，GDQ方法的基本做法如下:

(11)

其中，N是x方向上离散网格点的总数.Cijm是与第m阶导数相关的加权系数.选取x方向上余弦函数点作为离散网格点，即xi={1-cos[(i-1)/(N-1)π]}/2L，(i=1,2,…,N).显然，越靠近锥壳的端点，离散网格点的分布就越密集.值得注意的是，锥壳两个端点的坐标为x1=0和xN=L.V(x)和W(x)导数的离散表达式可与式(11)中U(x)的表达式类似.

将这些GDQ方法的表达式应用于常微分控制方程组[式(10)]，得到一组线性代数方程组:

(12)

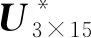
(13)

式中U(m)(xi)，V(m)(xi)和W(m)(xi)可分别由式(11)确定，且m=1,2,3,4.

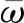
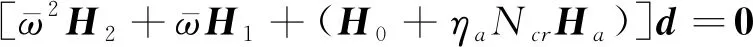
(14)

式中H0,H1,H2,Ha分别表示维度为系数矩阵J×J的系数矩阵(J=3N-8).需要说明的是，Ha仅由轴向力作用而引起的.d表示第J阶模态振型列向量，有

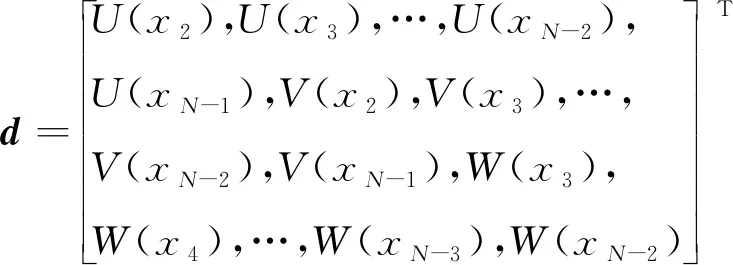
(15)

通过求解方程(14)的多项式特征值问题，可以得到给定转速下旋转锥壳的前后行波振动频率.在运动方程的推导中，锥壳的位移场可以视作

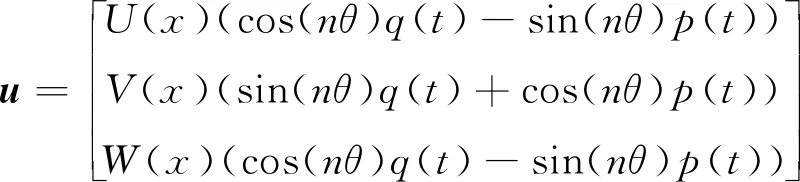
(16)

与多项式特征值问题的推导类似，旋转锥壳在周期性轴向载荷作用下的运动方程可表示如下:

(17)

式中f=[q1(t),q2(t), …,qJ(t),p1(t),p2(t), …,pJ(t)]T表示维度为2J×1广义自由度列向量，而质量、陀螺和刚度系数矩阵可表示为

(18)

显然，在考虑周期性轴向载荷的情况下，圆锥薄壳的控制方程具有Mathieu-Hill型的周期性变化系数.这类系统又称为参数激励系统，系统的参数稳定性是人们关注的主要问题.

2 参数稳定性分析方法

公式(17)的解的稳定性将通过Hill方法[25]进行研究.该方法基于Floquet理论，其主要思路是式(17)的解可以写成指数部分和周期部分的乘积.用复Fourier级数展开表示周期部分，这个解可以写成

(19)

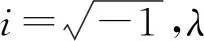
f=eλωatΦAn

(20)

(21)

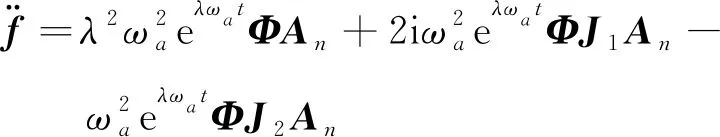
(22)

式中，J1=diag([…kI…])和J2=diag([…k2I…]).通过三角函数运算，cosωatΦ可重新表示为

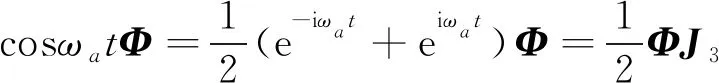
(23)

式中

(24)

将式(20)～式(24)代入式(17)，应用谐波平衡条件，得到如下代数方程:

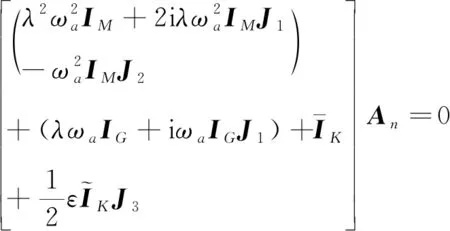
(25)

式中，IM=diag([…M…])，IG=diag([…G…])，IK=diag([…K0…])和IK=diag([…Ka…]).为了使式(17)具有式(19)形式的非零解，式(25)的系数矩阵的行列式需为零(ωa≠0):

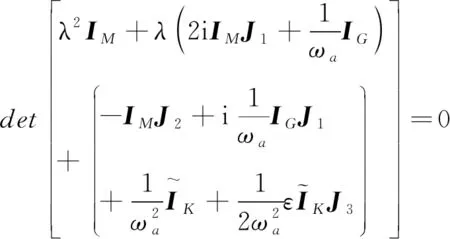
(26)

式(26)可用于分析给定轴向力的变化频率ωa和相对振幅ε的系统稳定性.如果系统是稳定的，所有特征值λ的实部为负，指数部分随着时间的推移而减小.另一方面，如果至少有一个特征值λ具有正实部，则系统是不稳定的.为了得到稳定分析的近似数值特征值，只需少量的Nk就可以满足精度要求.

3 分析实例

3.1 模型验证

在开展稳定性研究之前，需要对所提出的薄壁锥壳模型和GDQ方法的结果进行验证.采用ωs表示非旋转锥壳的固有频率.考虑旋转后，特定模态(m,n)的前/后行波频率用ωb和ωf表示，其中，n=1, 2, …表示周向波的数量，而m=1, 2, …则表示相应驻波模式中轴向半波的数量.以[ρa2(1-υ2)/E]1/2为转速、频率的量纲，则无量纲化后的转速和行波频率分别表示为Ω*,ωa*,ωs*,ωb*,ωf*.

表1给出了具有Cs-Cl和Ss-Sl边界条件的非旋转各向同性圆锥壳的固有频率ωs*的比较.以Irie等[27]的数值积分方法得到的结果为基准值，所分析的圆锥壳参数为m=1,υ=0.3,α=30°,h/a=0.01.结果表明，在增加离散网格点的情况下GDQ方法的结果很快得到收敛，且与文献结果具有较好的一致性.将旋转各向同性圆柱壳在不同转速下的前后行波频率与Sun等[28]的结果进行比较，如表2所示.结构参数为υ=0.3,α=0°,h=a/500,L=5a，边界条件为Ss-Sl.从中也可发现类似的一致性，表明本研究所建立的分析模型是正确的，用GDQ方法得到的固有频率结果是可信的.为了精度要求，在后续分析中将总网格点数设为16.

表1 不同边界条件时非旋转圆锥壳的固有频率比较

表2 旋转圆柱壳在不同转速下的前后行波频率比较

3.2 不同转速下的参数不稳定区

分析的圆锥薄壳参数为m=1,n=2,υ=0.3,α=20°,h/a=0.008,L/a=10，边界条件为Cs-Cl.计算了不同转速时周期轴向力作用下主参数不稳定区，如图2所示.考虑拉伸轴向力(ηa=0.2)，且相对变化幅值ε由0.05增加至0.5.可以看出，随着ε的增加，不稳定区域对称地扩大.与对称轴相对应的激励频率即为前后行波频率之和，即ωa*=ωb*+ωf*.显然，对于不旋转的锥壳，有ωa*=2ωs*.考虑旋转后，不稳定区域向高频率范围整体移动，尤其是当转速大于0.002时，如图4(c)所示.但在一定的转速范围内，不稳定区域的位置受转速的影响不大.当边界条件改为Ss-Sl、Cs-Sl或Ss-Cl时，也有类似现象.由于篇幅的限制，这里不给出结果.在后续分析中，只考虑Cs-Cl边界条件，并讨论系统参数对不稳定区域的影响.

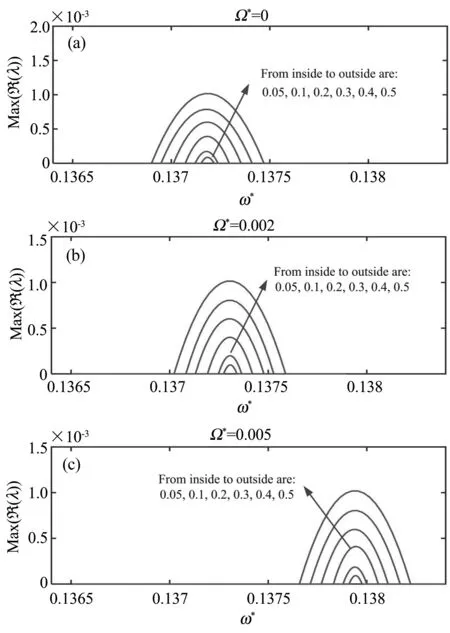
图2 不同转速时周期轴向力作用下旋转锥壳的主参数不稳定区

3.3 参数影响分析

3.3.1 定常轴向力幅值

图3绘制了具有不同定常轴向力幅值时对应不同模态的不稳定区域变化.考虑了三种轴向力幅值(ηa=0.1,0.2,0.3)，相对幅值固定为ε=0.5，转速为Ω*=0.005，其他参数与上一节模型参数相同.随着ηa的增加，不稳定区向高频区整体移动.这是由于增加恒定轴向载荷会增加固有频率值，进而使失稳区域的起始点向更高的频率范围移动.对于给定的ε，增加恒定轴向载荷ηa也会增加周期轴向载荷的变化幅值，刚度参数激励得到加强，使得不稳定区的范围有所扩大，如图3(a)所示.随着周向波数的增加[模态(1,3)和模态(1,4)，如图3(b)和图3(c)所示]，不稳定区的变化规律与模态(1,1)类似.

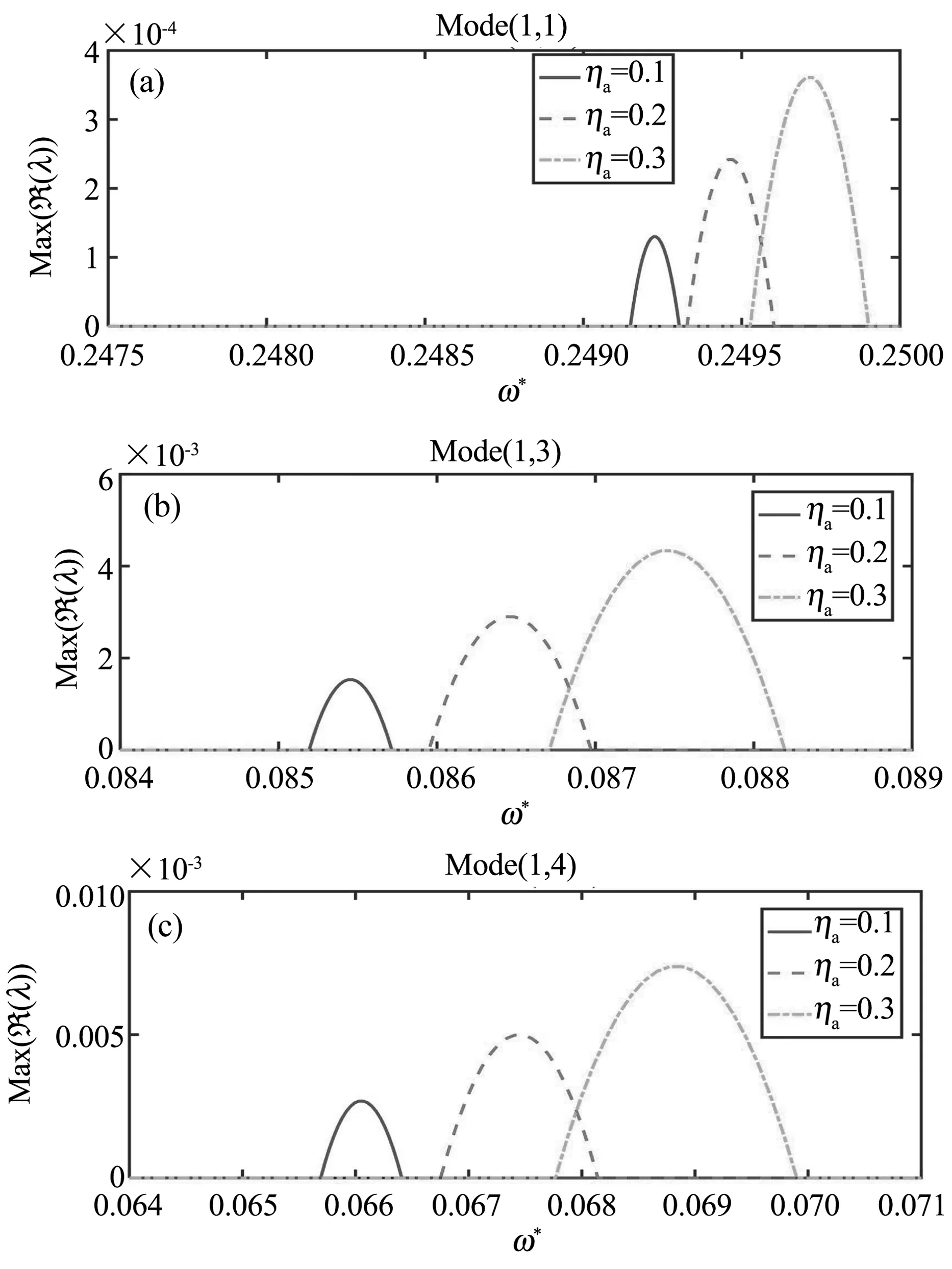
图3 定常轴向力幅值对不稳定区的影响

3.3.2 锥角

本节讨论锥角对不稳定区的影响.分析的圆锥薄壳参数为υ=0.3,h/a=0.008,L/a=10, Ω*=0.005,ηa=0.2,ε=0.5.考虑三种锥角值(α=20°, 40°, 60°)，结果如图4所示.对于模态(1,1)，增大α值，失稳区整体向低频段移动，且不稳定区范围有所扩大.对于模态(1,3)和模态(1,4)，首先使不稳定区域向高频段移动而后向低频段移动，如图4(b)和图4(c)所示.不稳定区范围也有所增加.与模态(1,1)的情况相比，模态(1,3)和模态(1,4)的不稳定区的移动和范围扩大量相对较小.这表明，随着周向波的增加，锥角对失稳区的影响呈减弱趋势.这一现象也与Ng等[9]的发现一致.

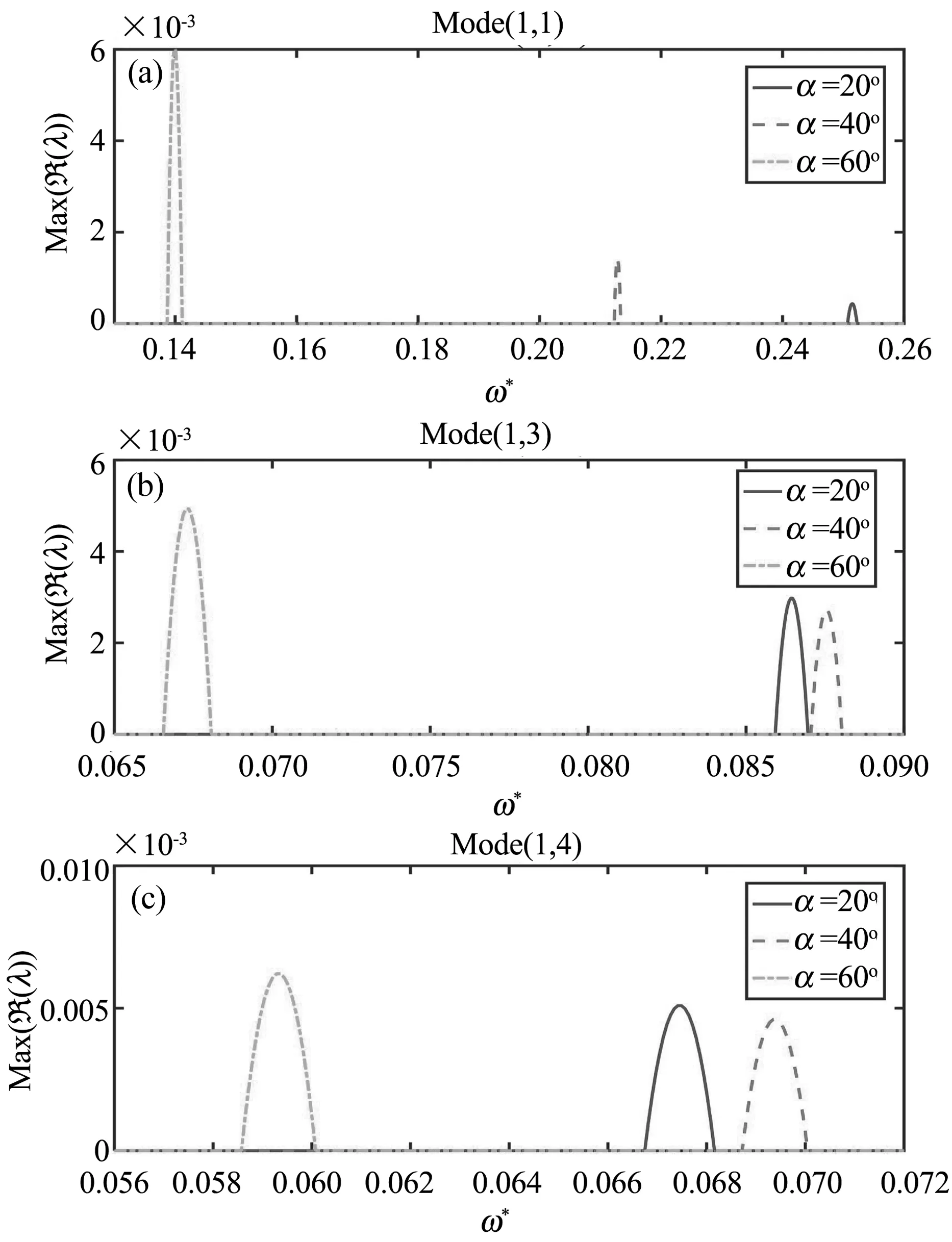
图4 锥角对不稳定区的影响

3.3.3 厚径比

本节研究厚径比对不同模态的不稳定区影响，如图5所示.分析的圆锥薄壳参数为υ=0.3,α=20°,L/a=10, Ω*=0.005,ηa=0.2,ε=0.5.分析了三种厚径比值，即h/a=0.005, 0.008, 0.012.结果表明，增大h/a值不仅会使不稳定区向高频段移动，而且会使不稳定区明显扩大.对于周向波较大的情况，如图5(c)所示的模态(1,4)，不稳定区随h/a的移动和扩大并未减弱.

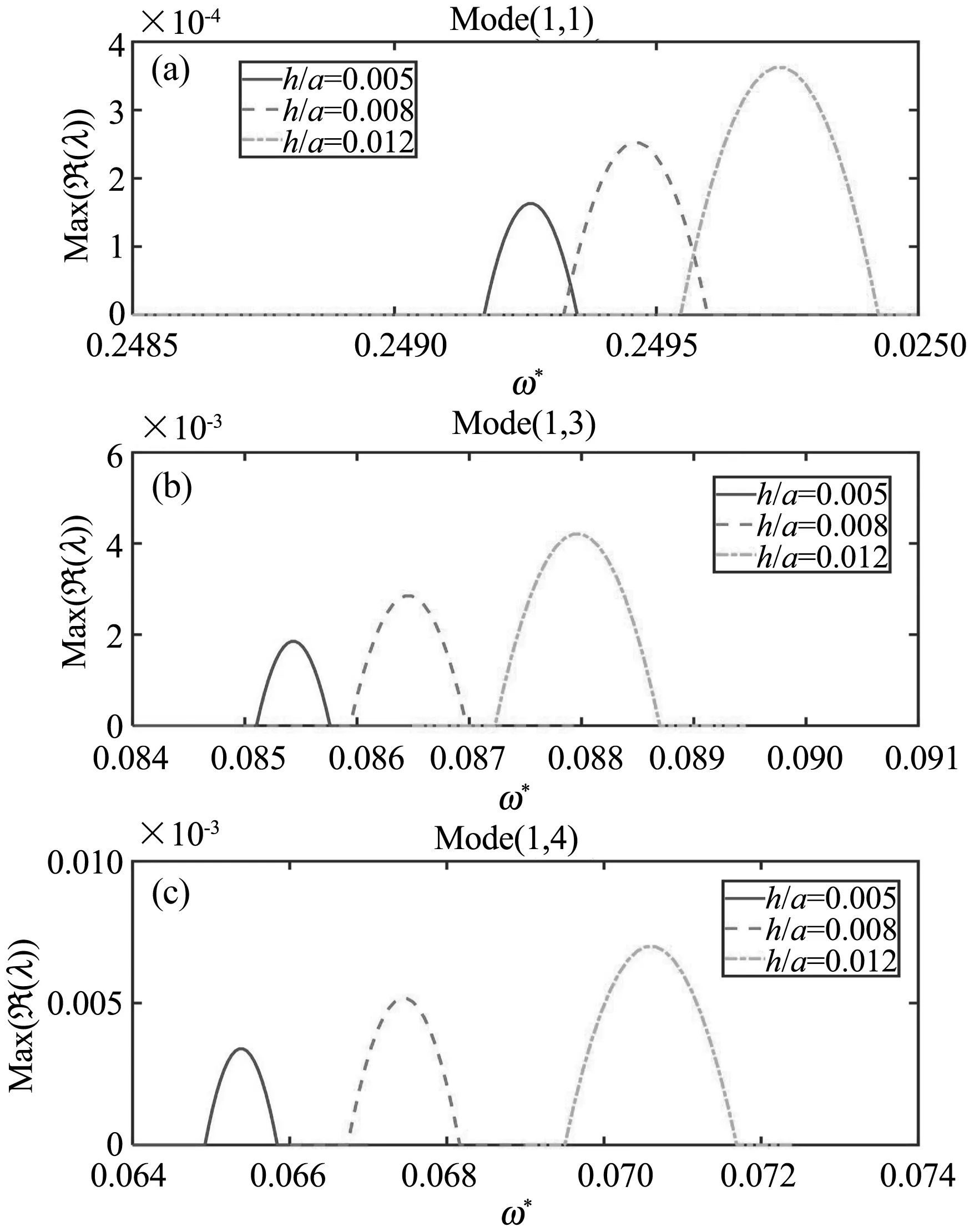
图5 厚径比对不稳定区的影响

3.3.4 长径比

讨论长径比对不稳定区的影响.分析的圆锥薄壳参数为υ=0.3,α=20°,h/a=0.008,Ω*=0.005,ηa=0.2,ε=0.5.当L/a=10, 15和20时，不稳定区的结果如图6所示.可以发现，随着L/a的增加，不稳定区主要出现在低频段.对于周向波数较少的失稳模态，如模态(1,1)，除失稳区的整体移动外，失稳区宽度的变化不大.但是，对于周向波数较多的失稳模态，增大L/a值也会减小失稳区宽度，如图6(c)所示.

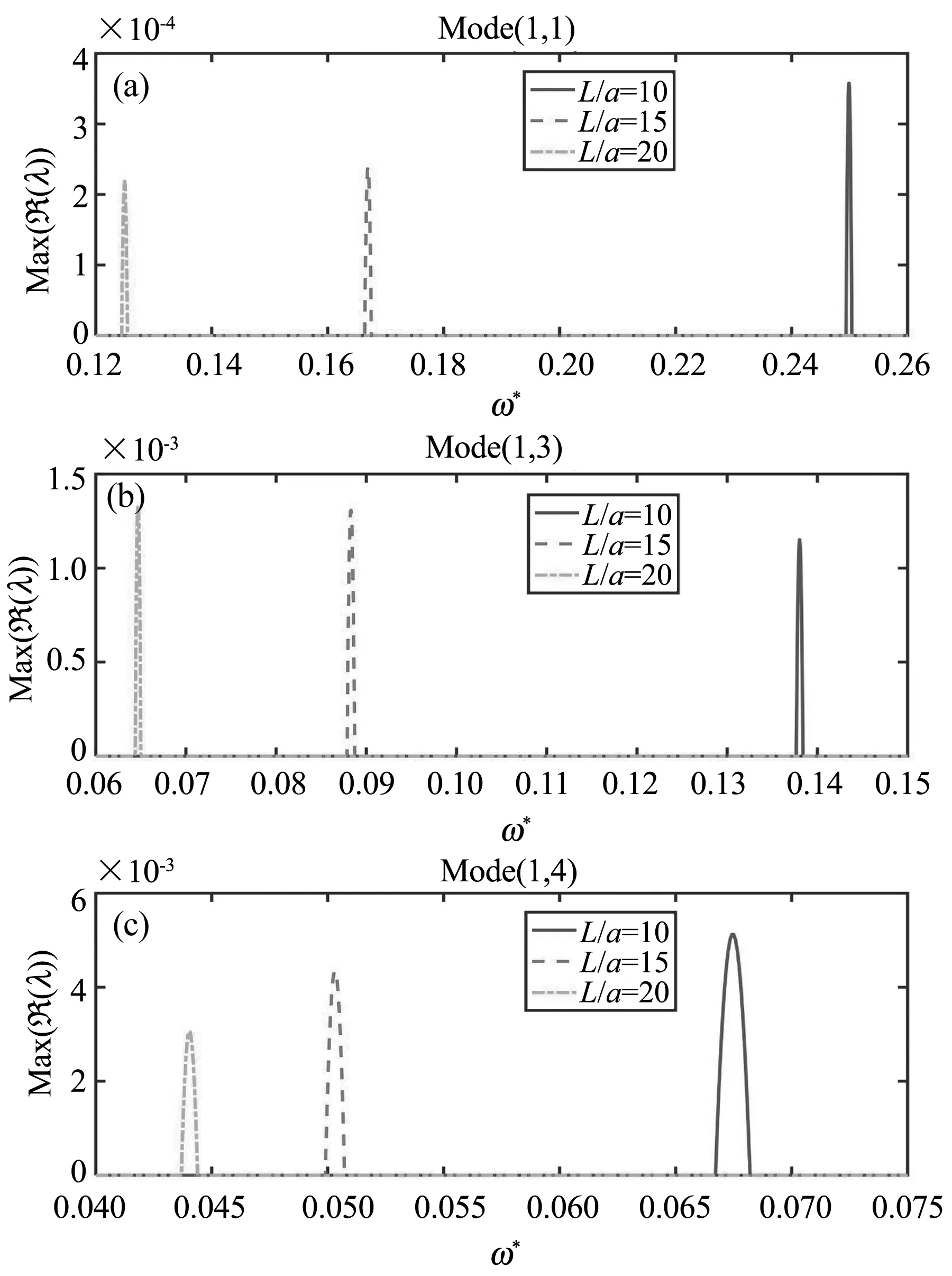
图6 长径比对不稳定区的影响

4 结论

本文首先推导了旋转锥壳的动力学方程，采用GDQ法和Hill法分析了系统在周期轴向载荷作用下的参数不稳定性.计算并讨论了多个不稳定区随工况和几何参数的变化规律.结果表明：提高转速会导致不稳定区沿频率轴移动，但对不稳定宽度影响不大.增加恒定拉伸轴向载荷，不仅会显著增加失稳宽度，而且会导致失稳区域向更高的频率范围移动.锥角、厚径比或长径比的变化都会导致不稳定区沿频率轴移动.锥角和厚径比会增大失稳宽度(长径比会减小).随着周向波个数的增加，锥角对失稳区的影响逐渐减弱，而厚径比的影响则基本保持不变.

上述研究基于线性和各向同性薄壁壳体假设.若壳体是非线性的且各向异性，例如考虑大变形、功能梯度或复合材料层合壳材料.进一步的工作应重点探讨非线性因素的引入对系统动力稳定性的影响.