遥操作旋转运动梁系统多目标优化控制研究*

李小乐 陈龙祥

(上海交通大学 船舶海洋与建筑工程学院，上海 200240)

引言

遥操作系统在航空、航天、医疗和海洋开发等领域有着广泛的应用前景[1-3].典型的遥操作系统由操作者、主端系统、通信信道、从端系统和从端环境几部分组成，操作者通过操控主端系统产生指令信号，该指令信号通过通信信道远距离传输给从端系统，从端系统接收指令后跟踪主端系统的运动与从端环境交互，并将从端环境的相关信息反馈给主端系统.因此遥操作控制系统一方面要保证主从端控制系统的稳定性，另一方面要求主端系统能够及时感受到从端环境的变化.远距离操控所面临的主要问题是从端系统与主端系统的通信过程中存在时间延迟，通信时滞对遥操作控制系统的稳定性和透明性造成了严重的不利影响[2-4].

为了消除时滞对遥操作系统的影响，常见的稳定性控制方法有无源性控制[4]、监督控制[5, 6]、基于事件的控制方法[7]、模型预测控制[8]、Lyapunov函数[9, 10]、局部自主控制[11]等.这些方法能够保证遥操作系统的稳定性和透明性，但是大部分都无法明确给出主从端系统跟踪误差的收敛速度[12].为平衡主从端系统跟踪误差收敛速度和系统稳定性的矛盾，许多学者对有限时间内遥操作系统的控制设计进行了研究[13, 14]，由于遥操作系统的控制目标相互冲突，有限时间控制设计方法往往只能获得某种程度上的控制性能最优.考虑到多目标优化控制设计方法可以根据所需要的控制目标获得对应控制增益的Pareto最优解集[15]，操作者可以根据需要选择合适的控制增益实现遥操作任务，这对提高遥操作系统的控制性能有很好的意义，而且目前对于遥操作系统的控制尚未见多目标优化相关研究报道.

本文基于Lyapunov稳定性，将多目标优化方法引入遥操作系统双边控制设计.第一节以旋转运动柔性梁为对象建立双边遥操作系统动力学模型；第二节采用Lyapunov稳定性理论得到保证遥操作闭环控制系统稳定的控制增益需要满足的条件；第三节采用基于胞映射的多目标优化方法获取保证系统实现控制目标的Pareto最优解集；第四节进行数值仿真并分析得出结论.

1 遥操作旋转运动柔性梁系统动力学模型

考虑如图1所示的遥操作旋转运动柔性梁系统，主端和从端均为在水平面内作回转运动的旋转运动柔性梁，系统信号传输中存在时滞，其中τm(t)为自主端到从端的信号传输时滞，τs(t)为自从端到主端的信号传输时滞.假定在旋转梁基座O处施加控制扭矩，以实现系统的大范围运动.同时在柔性梁根部施加控制力矩以控制柔性梁大范围运动中产生的弹性振动.忽略重力和摩擦的影响，基于Hamilton原理和假设模态离散化方法，主端和从端旋转运动柔性梁的一次近似动力学方程分别表示为[16]：

图1 遥操作旋转运动柔性梁系统

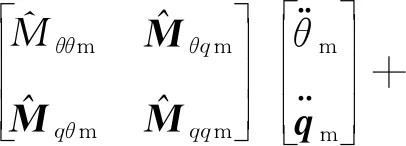
(1)

(2)

(3)

(4)

其中,uh0、ue0分别表示外部操作者和外界环境施加在主从端关节上的等效力矩；kh、ke和ch、ce分别表示主端与操作者、从端与外界环境间相互作用力的等效刚度和等效阻尼系数.

考虑方程(3)和方程(4)，并对方程(1)和方程(2)进行线性化，得到遥操作系统的线性化动力学方程为：

(5)

(6)

2 控制器设计和稳定性分析

如图1所示，遥操作系统通信网络中存在时滞，旋转运动柔性梁遥操作系统中主端与从端之间的误差可定义为：

em=ym(t)-ys(t-τs(t))

(7)

es=ys(t)-ym(t-τm(t))

(8)

控制设计的目的是使得从端系统尽可能快地跟踪主端系统的运动，并同时抑制柔性结构的振动，考虑误差(7)和误差(8)，如图2所示设计主端控制律和从端控制律分别如下：

图2 闭环遥操作系统控制示意图

(9)

(10)

其中，Kdi、Kpi和Kvi为控制增益，且Kli=dig(kl1,kl2,…,kln)>0(1=d,p,v).

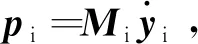
Kpmys(t-τs)+Kvmps(t-τs)+uh0

(11)

Kpsym(t-τm)+Kvspm(t-τm)-ue0

(12)

(13)

(14)

由于扰动方程(13)和方程(14)的零解与遥操作闭环系统的稳态解完全等价，因此下面考虑采用Lyapunov-Krasovskii泛函对闭环系统稳定性进行分析，同时设计相应的控制律.选取如下Lyapunov-Krasovskii泛函[9]：

V=V1+V2+V3

(15)

其中：

其中，P为对称正定矩阵.

将V1关于时间t沿扰动方程(13)和方程(14)求导得：

(16)

方程(16)利用不等式关系2aTb≤aTM-1a+bTMb，有

PXm(t-τm)

(17)

将V2关于时间t沿扰动方程(13)和方程(14)求导，可得：

(18)

将V3关于时间t沿扰动方程(13)和方程(14)求导得：

(19)

整理方程(17)～方程(19)，可得：

(20)

(21)

(22)

3 多目标优化控制设计

方程(21)和方程(22)所得到的控制增益能够保证遥操作闭环控制系统稳定，但无法判断所给出的控制增益的控制效果，而且在直接求解控制增益上有一定的困难.控制设计要求从端系统较好地跟踪主端系统的运动，同时能够有效地抑制柔性结构的振动，这两个目标之间存在一定的矛盾.为协调这一矛盾，同时获得具体的最优控制增益集，下面基于方程(21)和方程(22)采用基于胞映射的多目标优化控制设计方法[15]进行控制设计.

由于方程(21)和方程(22)具有相同的形式，为减少多目标优化计算时间，假定主端和从端具有相同的控制增益，Kvi中对角线元素相同均为kv，考虑一阶模态，则所设计的控制增益向量为：

K=[kp1,kp2,kd1,kd2,kv]T

(23)

其中，元素kp1，kp2，kd1，kd2分别为方程(9)和(10)中Kpi和Kdi的对角线元素，且控制增益满足约束关系方程(21)和方程(22).

遥操作系统多目标优化设计问题可表述为：

(24)

其中，ts,θ为主端柔性梁的振动趋向于0所需时间，eIAE为主从端大范围运动误差绝对值的积分，即

(25)

其中，Tss为系统大范围运动趋近稳定状态的时间.

4 数值仿真

为验证所设计控制器的有效性，进行数值仿真验证.考虑主端旋转运动梁与从端旋转运动梁参数相同的情况，旋转关节半径为0.03 m，对转轴转动惯量为0.000765 kg·m2，柔性梁尺寸为0.7 m×0.0395 m×0.0018 m，材料密度为2150 kg/m3，弹性模量为28.0 GPa.

首先采用基于胞映射的多目标优化控制设计，此时假定从端环境自由，外界操作者施加在主端关节上的力矩为0.04 N·m，操作者与主端相互作用力的等效刚度为0.1 N·m/rad，从而保证主端大范围运动角度为0.4 rad时操作者施加在主端的力矩为零.为便于优化，最大时滞量hm=0.5 s和hs=0.4 s为优化过程中遥操作系统的信号传输时滞，时滞变化率均为零.选取参数空间如下：

Q={K∈R5|[-0.0275,-17.8275,1.51, 1.51,-0.0375]≤pK≤p[0.1275, 20, 2.51, 202, 0.1875]}

(26)

将参数空间划分为3×5×4×8×3个胞，对多目标优化控制目标(24)的约束条件为：

[ts,θ,eIAE]≤p[17 s,0.7 rad]

(27)

同时控制增益之间的关系需要满足方程(21)和方程(22).

通过优化在给定区间内得到的Pareto最优解集共8组，表1给出某一项指标最优时所获得的控制增益.图3给出了多目标优化所得到的最优解与对应目标函数之间的关系.利用表1和图3，可以根据需要选择合适的控制增益参数对遥操作系统进行有效的控制.由于将方程(21)和方程(22)引入多目标优化设计，原本1440个单元需要约2880min的计算量减少仅需计算208个单元为416min，极大地节省了多目标优化的时间.

表1 极端控制设计所对应控制增益

图3 Pareto解集与控制目标关系图

为更好地说明控制的有效性，K=[0.1081,-1.2780,2.3433,21.5590,0.15]为图3中框点对应的控制增益，其控制目标为[ts,θ,eIAE]=[8.2220 s,0.4066 rad].相比控制增益中不考虑Kvi的情况，所对应的控制目标为[ts,θ,eIAE]=[8.2780 s,0.4172 rad]，本文所设计的控制器取得了更好的控制效果.

然后考虑外部操作者施加在主端关节上的等效力矩uh0的不同对控制效果的影响.假定系统运动工况与多目标优化时相同，即从端环境自由，操作者与主端相互作用力的等效刚度为0.1 N·m/rad.图4给出了外界操作者施加在主端关节上的等效力矩分别为0.04 N·m，0.06 N·m，0.08 N·m以及0.10 N·m时的控制响应.由图4可以看出，所设计的控制器能够保证遥操作系统的控制效果，但随着主端关节处施加力矩的增大，主从端系统响应的跟踪时间及相对误差也会增加，可见随主端受驱动运动角速度的增大，受时间延迟影响，从端在控制下跟踪的难度会随之加大.

图4 主端不同操作力矩时系统主从端响应

下面考虑不同工况下控制效果的有效性，在0～20s内系统处于自由状态，即主从端系统初始位置不同，主端操作者和从端环境无外部施加力，主端关节初始转角为0，从端关节转角为0.3rad；20～40s内从端与外界环境间作用力中ke=0.1 N·m/rad，40～60s内从端环境受到等效力矩ue0=0.02 N·m.图5给出了信号传输时滞量为常时滞τm=0.5 s，τs=0.4 s时主从端系统关节转角和柔性梁末端变形跟踪曲线和跟踪误差曲线.图6给出了信号传输时滞量为时变时滞τm=(0.25+0.125sin (0.02t)) s，τs=(0.2+0.1sin(0.02t)) s时主从端系统跟踪情况.由图5和图6可以看出，在受到时滞和从端外部环境的影响时，本文所提出的方法能够使得从端系统有效地跟踪主端系统的运动.

图5 主从端旋转柔性梁关节转角和梁末端跟踪曲线(τm=0.5 s，τs=0.4 s)

图6 时变时滞下主从端旋转柔性梁关节转角和梁末端跟踪曲线(τm=(0.25+0.125sin (0.02t)) s，τs=(0.2+0.1sin (0.02t)) s)

考虑从端与刚性墙壁接触的情况，假定主从端机械臂初始时均处于θm=θs=0.4 rad位置，主端操作者在柔性梁末端y0方向施加大小为0.005 N的力使系统开始运动，当从端柔性梁末端运动到y0=0.4 m处梁末端与刚性墙壁发生接触，为保证接触后柔性梁与墙壁不再发生分离，通过仿真定义该接触为Fe=20×(y-y0) N，其中y为从端梁末端在y0方向上位移[18]，然后将接触力当作外力考虑，等效为控制力矩施加于方程(5)和方程(6)中，仿真中信号传输时滞量为τm=0.5 s，τs=0.4 s.图7给出了遥操作系统与刚性墙壁发生碰撞时主从端关节转角和末端变形跟踪情况.由图中可以看出，大约6s从端机械臂与墙面发生接触，由于传输时滞和主端受到恒定力的影响，主端继续运动，当从端信号返回主端后，主端在控制力的作用下停止移动，从端与刚性壁的接触情况及时反馈到主端系统.仿真结果可以看出系统稳定后主从端系统保持固定有界的跟踪误差且柔性部件的弹性振动得到有效的抑制，反映了所设计控制器的有效性.

图7 与刚性墙壁发生接触，主从端旋转柔性梁关节转角和梁末端跟踪曲线

最后考虑主从端结构参数存在差异的情况，假定其他参数相同的情况下，改变从端柔性机械臂尺寸为0.9 m×0.0295 m×0.0018 m，此时主从端柔性梁一阶固有频率分别为13.10 Hz及7.92 Hz.首先对主从端刚度不同的遥操作系统进行多目标优化控制设计.多目标优化中参数空间、空间划分及优化目标与方程(26)和方程(27)相同.通过优化得到的Pareto最优解集共11组，图8给出了多目标优化所得到的最优解与对应目标函数之间的关系，从图3和图8中可以看出，当主从端结构参数出现差异时，与主从端结构参数相同的遥操作系统相比，Pareto解集中控制系统跟踪时间和跟踪误差都会增加，因此更需要选择合适的控制增益对遥操作系统进行控制.然后利用图8框点处所对应的控制增益K=[0.1081,-1.2780,2.0100,21.5590,0.15]进行主从端结构不同工况下的数值仿真，由图9所示主从端跟踪情况可以看出，当主从端梁柔性存在差异时，本文所提出的控制方法能够使得从端系统有效地跟踪主端系统的运动.

图8 Pareto解集与控制目标关系图

图9 主从端旋转柔性梁关节转角和梁末端跟踪曲线(主从端参数不同时)

5 结论

基于稳定性理论，本文采用多目标优化控制方法对遥操作旋转运动柔性梁系统进行双边控制研究.首先利用Lyapunov稳定性理论获得保证遥操作闭环控制系统稳定的条件，然后采用多目标优化控制设计获得有效控制遥操作系统的控制增益.研究表明稳定性条件能够有效地减少多目标优化的计算时间，而基于胞映射的多目标优化方法能够在所给参数空间获得满足控制目标的Pareto最优控制增益集，能够更有效地对遥操作系统进行控制.考虑时滞变化和从端刚性接触的仿真结果表明本文所获得的控制增益能够保证从端系统对主端系统进行有效的跟踪，而且从端环境的变化能够及时有效地反馈到主端系统.