空间平台发射服务器动力学与双脉冲最优交会*
韩艳铧 李伟康 张勇
(1.南京航空航天大学 航天学院,南京 211106)(2.南京航空航天大学 无人机研究院, 南京 210016)(3.南京航空航天大学 中小型无人机先进技术工业和信息化部重点实验室,南京 210016)
引言
基于交会对接的在轨维护技术对于航天工程意义重大,是当前和今后航天领域重要研究课题.脉冲法制导,因其原理和算法相对简单,易于工程实现,在推力作用时间远小于航天器惯性滑行时间条件下,制导误差很小,故在空间交会对接领域颇受重视[1-5].空间交会对接任务中,能量和时间是宝贵资源,吸引众多学者开展了最优制导的研究[6-11].其中,文献[6] 针对同时受时间与燃料约束的航天器多轨道间机动问题,研究了两类变轨机动方式四种特殊情况的边界问题;文献[7]研究了时间最优多脉冲交会问题中最优交会时间和脉冲数随各因素的变化规律,并根据最优交会时间随各因素变化曲线较为“平缓”的事实,提出可以利用较少的特征点通过插值方法快速求解最优交会的策略;文献[8]研究了多脉冲燃耗最省圆轨道调相问题,以线性近似模型的精确最优解作为真实非线性动力学情形下优化解的迭代初值,以提高收敛速度;文献[10]针对燃料受限多脉冲时间最优轨道控制,提出一种解析法和数值法相结合的方法,解决了最优控制间接法微分方程两点边值问题协态变量的初值猜测问题,能够得到充分接近真实最优解的近似解,然后用数值法求解,并以深空探测变轨控制作了仿真验证.
无论是脉冲制导还是连续推力制导,凡涉及最优策略往往计算量较大,难以在线实现,基于小参数摄动的近似优化制导在航天领域应运而生,譬如文献[12-13]将大气标高与地球半径之比作为小参数,用正则摄动法研究了拦截弹道导弹的时间最优制导律.采用摄动法得到的近似优化解与真实最优解非常接近,但计算量大大减轻,容易在线实现.
空间平台装载多个服务航天器(譬如空间机器人,下文简称服务器),平时在轨驻留,接到任务指令后机动到目标星附近,与目标星形成近距离绕飞关系,然后发射服务器到目标星,与目标星交会对接,执行维护任务.完成任务后,平台继续在轨待命为下一次任务做准备.本文研究这种场景下空间平台发射服务器动力学以及服务器分离后与目标星的最优交会制导问题.从国内外研究动态来看,专门针对服务器与目标星近距离相对飞行特点,引入小参数正则摄动的方法进行双脉冲优化制导的研究还未见诸报道.
平台绕飞目标星的椭圆相对轨道的尺度一般在数十米至数百米,以保证平台上的光学等导航设备可实时测得相对于目标星的飞行状态信息.绕飞过程中平台的姿控系统维持其发射筒轴线始终瞄准目标星.服务器从发射筒分离后,自身的小型火箭发动机给其施加首末两次速度脉冲:首次脉冲修正其飞行速度,保证服务器凭惯性飞达目标星,末次脉冲将其相对速度减为零,实现与目标星的软对接,如图1所示.

图1 平台绕飞并瞄准目标星示意图
图2给出了服务器在平台中的装载几何.一个平台可以装载多个服务器,形成一个矩阵,满载服务器的列数和行数分别为nx和ny.安装有机械手的一面表示发射方向.图中:lr的意义如图所示;dr表示服务器的直径,并且定义每个服务器的质心到其底部的距离为lcg;dy表示服务器与所在发射筒底部之间的间隙;dx表示发射筒壁的厚度.假设平台本体质心在其几何中心.

图2 平台装载服务器示意图
服务器双脉冲交会对接制导的性能指标是能耗最省,即两次脉冲速度幅值的平方和最小,构成一个非线性规划问题.文本采用小参数摄动法,快速求解出最优双脉冲的一阶近似解,并以此为迭代初值,用非线性规划方法快速可靠地收敛到最优真解.
1 发射过程平台-服务器两体动力学
首先建立目标星轨道坐标系OAxAyA:原点固定于目标星,xA轴正方向沿着目标星绕地速度方向,yA轴垂直于xA轴且背离地心方向为正.再建立平台本体系OBxByB:原点在平台质心,yB轴沿平台上的发射筒轴线方向,且以发射方向为正,xB轴垂直于yB轴,且在图2中向右为正.以上两坐标系在下文中分别简称为A系和B系.以目标星轨道坐标系的yA轴表示平台姿态偏航角的参考方向,且以右手规则定义偏航角的正负,在图1和2中即逆时针偏航为正.
相应于两个坐标系,定义基矢量组(下文简称基组)如下
A≜(a1,a2)
(1)
B≜(b1,b2)
(2)
其中a1,a2和b1,b2分别是坐标系A和 B的x,y两轴上的单位矢量,指向与相应的坐标轴正向一致.
两个基组之间的过渡关系如下:
B=ATAB
(3)
其中
(4)
η是平台的姿态偏航角.
我们知道,A系以角速度n旋转,其中n是目标星绕地圆轨道的角速度.根据近距离航天器相对运动的C-W方程理论,n也是平台绕飞目标星的平均角速度,故严格说来A系是非惯性系.但在建立平台发射服务器的动力学方程时,因为发射过程耗时与A系的旋转周期T=2π/n相比是很小的数,或等价地说,非惯性系A的旋转角速度n很小,可视A系为惯性系,由此引起的建模误差极小.
设平台质心相对于A系原点的位矢为
rp≜A(x,y)T
(5)
从平台左下角数起,服务器所在列数的递增方向是从左往右,所在行数的递增方向是从下往上.
第i列j行的服务器若固定在平台上,则其质心相对于平台质心的位矢为
(6)
根据图2不难算出
(7)
平台与所有固定的服务器形成一个刚体,称作总刚体,记作Σ.
设平台和单个服务器的质量分别为mp和mr,则根据多体系统质心的定义,总刚体质心相对于平台质心的位矢为
(8)
其中
(9)
是总刚体的质量.
(10)
下面计算总刚体关于自身质心的转动惯量.
设平台关于自身质心的转动惯量为Jp,则根据平行移轴定理,平台关于总刚体质心的转动惯量为
(11)
第i列j行的服务器质心相对于总刚体质心的位矢
(12)
设单个服务器关于自身质心的转动惯量为Jr,则根据平行移轴定理,其关于总刚体质心的转动惯量
(13)
总刚体关于自身质心的转动惯量
(14)
总刚体质心相对于A系原点的位矢
(15)
将相关各式代入上式得
rΣ=A(xΣ,A,yΣ,A)T
(16)
其中
(17)
式(16)对时间求两阶导,得总刚体质心相对于A系原点的加速度
aΣ≜A(axΣ,A,ayΣ,A)T
(18)
其中
(19)
式中
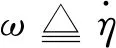
(20)
表示平台的姿态偏航角速率.
设第u列w行的服务器正在发射筒里发射滑行,其沿发射筒轴向的滑行位移为s(相对于初始固定时的位置),其质心相对于平台质心的位矢为
(21)
根据图2不难算出
(22)
其相对于惯性系原点的位矢
(23)
将相关各式代入上式得
ruw=A(xuw,A,yuw,A)T
(24)
其中
(25)
式(24)对时间求两阶导,得运动服务器质心相对于A系原点的加速度
auw≜A(axuw,A,ayuw,A)T
(26)
其中
(27)
下面分析系统中的主动力.
设平台受到的主发动机推力为
F≜B(Fx,Fy)T
(28)
并假设其过平台质心.
姿态控制力矩为
M≜b3M
(29)
其中
b3≜b1×b2
(30)
平台对正在发射滑行的服务器的推力为
f≜B(0,f)T
(31)
根据前文给出的基组间的过渡关系,上式变换到A系下
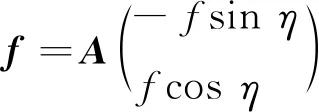
(32)
总刚体受到的主动力为
FΣ=F-f
(33)
将相关各式代入该式并变换到A系下
(34)
总刚体受到的主动力矩为
MΣ=M+MF+Mf
(35)
其中MF和Mf分别表示F和-f关于总刚体质心的力矩,计算公式如下
(36)
(37)
其中
(38)
将相关各式代入式(35)得
(39)
定义广义坐标
q≜(q1,q2,q3,q4)T≜(x,y,η,s)T
(40)
凯恩方法中的投影因子(偏速度和偏角速度)为
(41)
(42)
(43)
其中
ω≜b3ω=a3ω
(44)
根据凯恩方法,把系统中所有主动力(矩)、惯性力(矩)分别投影在四个广义坐标曲线的切线方向:
(i=1,2,3,4)
(45)
将相关各式代入式(45)得
(46)
2 服务器与目标星交会对接最优双脉冲制导
我们知道,当目标星在绕地圆轨道上且追踪星与其距离较近时,追踪星相对于目标星的运动满足C-W方程
(47)
该方程是在A系建立的,其中n是目标星绕地圆轨道的角速度,如果追踪星与目标星形成绕飞关系,则n也是追踪星环绕目标星的平均角速度.
式(47)的解析解为
(48)
和
(49)
其中,(x0,y0)表示追踪星初始相对位置坐标,(vx0,vy0)表示其初始相对速度.
若初始状态满足
(50)
则追踪星在以目标星为中心的相对椭圆轨道上绕飞.

(51)
该速度能保证服务器精准飞达目标星.
在服务器飞达目标星瞬间,再给其施加速度脉冲(Δvxf,Δvyf),使其相对速度减为零,与目标星软对接.
本文的任务是,寻求最优的速度双脉冲(Δvx0,Δvy0)和(Δvxf,Δvyf),保证服务器与目标星精准交会和软对接的前提下,所需能耗最省,即两次速度脉冲幅值平方和最小.用最优控制语言描述,即
(52)
其中
(53)
引入拉格朗日乘子μ1~μ4,则上述约束优化问题解的必要条件如下
(54)
当小参数n=0时,优化问题式(52)退化为
(55)
很容易得到优化问题式(55)的解,称为原优化问题的零阶近似解,如下
(56)
其中右上角标0表示“零阶近似”
令方程组(54)中头四式中的n=0,并将上述零阶近似优化解代入得
(57)
从中解得原优化问题拉格朗日乘子的零阶近似解如下
(58)
式(54)在变量Δvx0,Δvy0,Δvxf,Δvyf,tf,μ1~μ4的零阶近似解上和小参数n=0取值点上作一阶摄动(即一阶微分,用δ表示),得
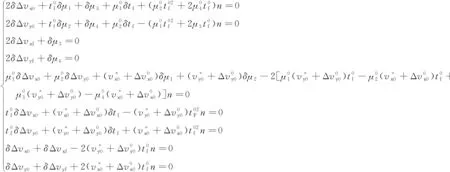
(59)
这是一个线性方程组,很易从中解出δΔvx0,δΔvy0,δΔvxf,δΔvyf,δμ1~δμ4,δtf,然后对式(56)表示的零阶近似优化解进行修正,得到一阶近似优化解,如下
(60)

3 仿真计算
仿真入口参数如表1所示.

表1 仿真入口参数
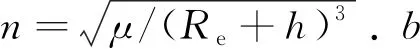
另外,本文所研究的是共面轨道内的交会制导问题,设目标星、平台、服务器所在轨道共面,其升交点赤经均为115°,轨道倾角均为45°.目标星圆轨道的半径为6.7710×106(m);平台所在椭圆轨道的半长轴、偏心率、近地点角距分别为6.7720×106(m)、2.2153×10-4、60°,发射服务器瞬间其真近点角为0°;服务器在获得首次速度脉冲后所在椭圆轨道的半长轴、偏心率、近地点角距分别为6.7716×106(m)、2.1755×10-4、20.24°,并且此刻服务器的真近点角为39.76°.
不失一般性,本仿真以图2中发射第1列第2行服务器为例.仿真结果如图3~10所示.

图3 发射过程平台运动轨迹
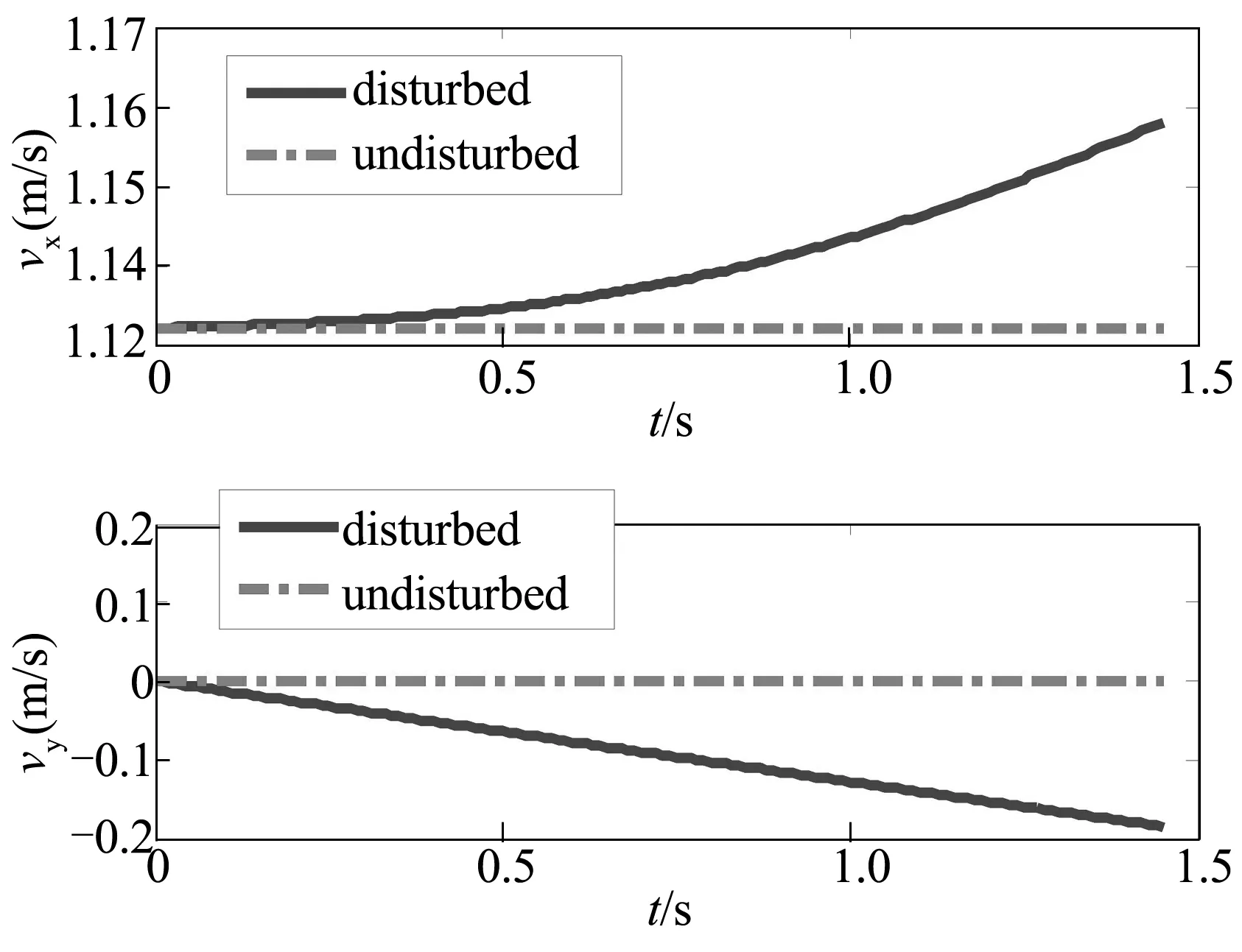
图4 发射过程平台速度
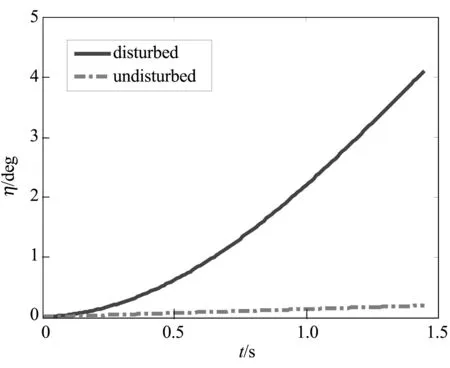
图5 发射过程平台姿态偏航角
图3~图6中的点划线表示假设平台未发射服务器,围绕目标星作相对椭圆运动,并且时刻保持发射筒轴线瞄准目标星时的运动情况,实线表示平台发射服务器,两体干扰下的实际运动状态,两种曲线分别用“undisturbed”和“disturbed”标识.
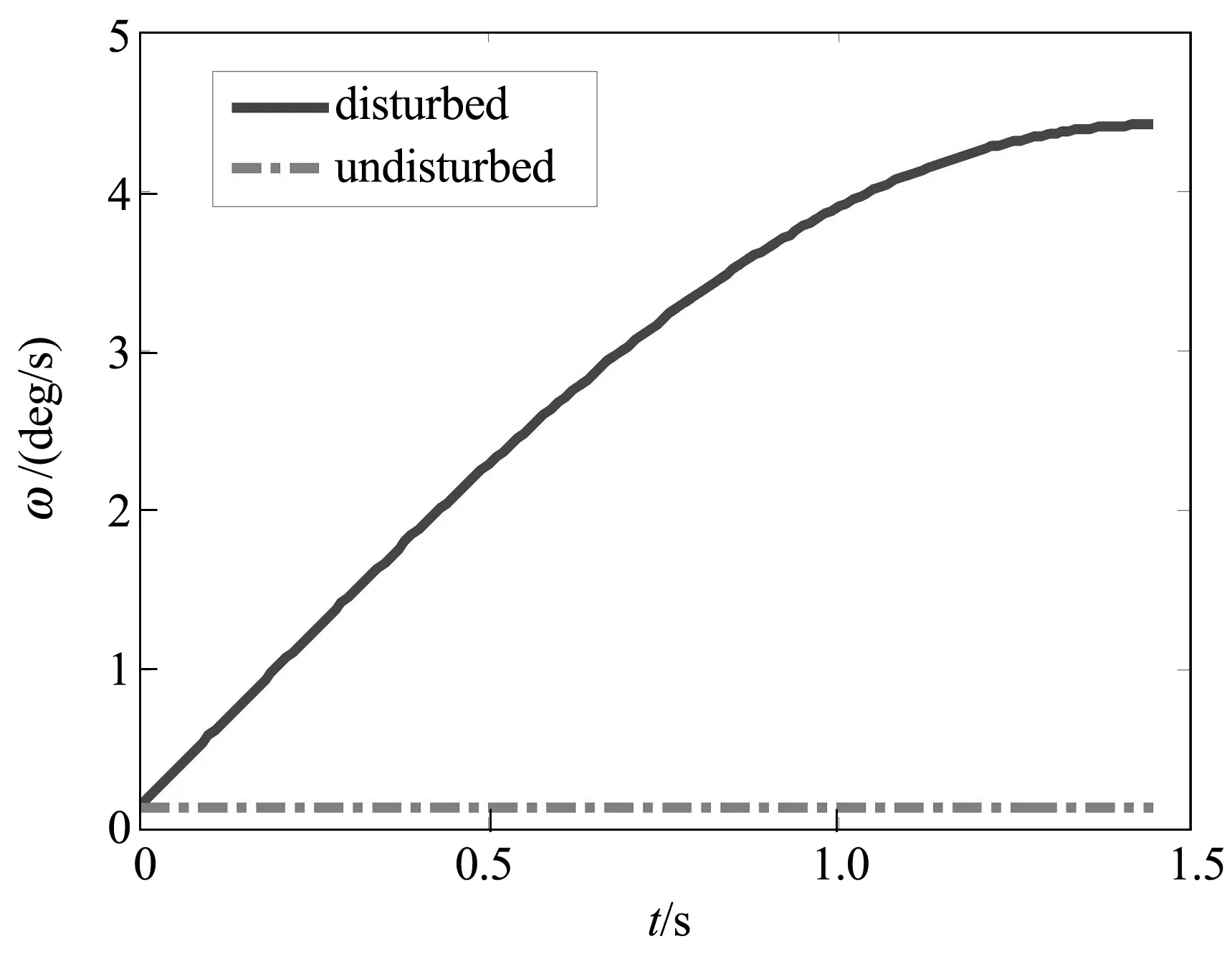
图6 发射过程平台姿态偏航角速率

图7 服务器在平台发射筒中的滑行位移
图3~图6显示,由于发射过程服务器对平台的反作用力,在服务器分离瞬间,平台的实际轨迹相对于未受扰的轨迹沿y轴负方向偏离了0.13(m),平台的x轴向相对速度增加了0.03(m/s),y轴向相对速度减小了0.19(m/s),姿态偏航角增加了3.91°,姿态偏航角速率增加了4.29(deg/s).考虑到平台相对于目标星的环绕椭圆的几何尺度和相对环绕速度,可认为服务器发射过程对平台位置坐标影响甚微,但对平台绕飞速度以及姿态的影响不容忽视.

图8 服务器在平台发射筒中的滑行速率

图9 服务器分离后在交会轨道上的位置坐标


图10 服务器分离后的交会轨道和速度脉冲
计算表明,首次速度脉冲与服务器离开平台瞬间的速度矢量夹角为167°.夹角为钝角表明,首次速度脉冲在改变服务器飞行速度方向的同时,在很大程度上起到减速制动作用.至于末端的二次速度脉冲,因为要将服务器相对于目标星的速度减为零,故其与服务器飞抵目标星瞬间的速度矢量必然等幅反向,夹角为180°,从图10也可以直观看出来.
两次速度脉冲均起到减速作用,这是由交会问题特殊的末端约束条件(相对速度为零)和能耗最省的性能指标共同导致的.
4 结论
本文针对空间平台绕飞目标星,对发射服务器与目标星实现精准交会和软对接的动力学与脉冲最优控制问题开展研究.在平台与目标星已形成绕飞关系的条件下,服务器从平台中射出,分离瞬间给其施加一个速度脉冲修正其飞行速度,然后服务器在C-W方程支配下凭惯性飞行,直至与目标星交会,此时再给其施加末端速度脉冲,使其相对速度减为零以实现软对接.本文采用凯恩方法建立了平台发射服务器过程的两体耦合动力学模型,然后基于小参数正则摄动法给出了最优速度脉冲的一阶近似优化解,并以此为迭代初值,采用非线性规划方法算得能耗最省双脉冲最优解.最后用数值仿真验证了本文所提方法的有效性.

