流星体与空间碎片模型综述*
姜宇 姜春生 李恒年
(1.宇航动力学国家重点实验室,西安 710043) (2. 西安卫星测控中心,西安 710043)
引言
随着人类探索太空的不断深入,发射任务逐渐增多,太空环境也越来越拥挤,这其中包括自然存在的流星体,也包括众多的空间碎片.太空环境中存在的流星体和绕轨道运行的空间碎片目前已经影响到太空任务,并且很可能成为未来太空飞行需要考虑的一个主要方面.
空间中流星体有三个不同的来源:彗星活动喷射的气体或核碎片,小行星的相互碰撞或旋转分裂以及星际空间的粒子.1961年,国际天文学联合会将流星体定义为“在行星际空间中运动的固体物体,其尺寸比小行星小得多,但比原子大得多”[1].1995年,Beech和Steel[2]在《皇家天文学会季刊》上撰文提出了一个新定义,即流星体的直径介于100μm和10m之间.2010 年,在发现小于10m的小行星后,Rubin和Grossman提议将之前对流星体的定义修改为直径在10μm和1m之间的物体,以保持区别[3].根据Rubin和Grossman的说法,最小尺寸的小行星是能被地球上的望远镜发现的,所以流星体和小行星之间的区别是模糊的.
与流星体环境相比,空间碎片环境主要是人为造成的.它由不活动的卫星或航天器、非运行有效载荷、分离程序、火箭意外爆炸、反卫星测试产生的碎片组成.自1957年首颗人造卫星发射以来,空间碎片一直在地球轨道上堆积.随着人类航天活动的蓬勃发展, 空间碎片环境日益恶化, 空间碎片相比于流星体,对航天器的安全运行威胁更大.截至2021年,空间中直径大于10cm的碎片约有3.65万个,直径在1cm和10cm之间的碎片超过100万个,而直径在1mm和1cm之间的碎片数量超过3.3亿[4].这其中,一部分是已编目的,而绝大部分是未编目的碎片.对于低轨区域,碎片的平均速度约为10km/s,而在倾角较大的极轨,如果碎片与航天器发生碰撞,碰撞速度将达到13km/s[5,6].对于航天器而言,可以在其表面安装保护墙来抵挡一些直径在1cm以下的物体碰撞带来的影响.然而,对于直径为1cm到10cm的物体,一旦其与航天器发生碰撞,很可能会摧毁航天器,而安装厚度过厚的保护层会降低航天器的实际负载率,对于高轨任务来说,这样的做法无疑会大大增加燃料消耗.而在某些空间区域,碎片密度已达到很高的状态,一旦发生碰撞,将导致级联效应,这种类型的碎片事件称为“凯斯勒现象”,在这种碰撞过程中产生的碎片可能会再次引发新的灾难性碰撞.
据估计,每天有2500万颗流星体、微流星体和其他空间碎片进入地球大气层[7],这导致每年约有15000吨这种物质进入大气层.因此,对流星体和空间碎片的环境模型进行研究对于航天器的保护是十分必要的.随着航天器轨道高度的不断提升以及行星际等具有挑战性任务的增多,流星体和碎片撞击风险评估成为使用最少量微流星体/空间碎片屏蔽来确保子系统、任务或机组人员安全的必要条件.由于这些空间物体数量较大,仅通过测量无法提供流星体/碎片群的完整变化情况,故必须利用适当的模型对群的演化进行估计.
1 流星体模型
流星体是行星际或星际起源的固体粒子.流星体的超高速撞击会对航天器和/或执行任务的宇航员构成重大危害.流星体撞击造成的损害取决于撞击粒子相对航天器外表面元件的大小、密度、孔隙率、速度和方向.微米级到亚毫米级粒子的反复冲击可能导致航天器表面材料因侵蚀或撞击形成的陨石坑而逐渐退化,诸如太阳能板和传感器等.较大的颗粒可以刺穿绝缘层和光学挡板.而更大的,具有足够动能的微流星体可以刺穿载人舱、推进器、电池、冷却剂管线或宇航服,以及切断电缆、系绳和弹簧.毫米大小的颗粒能够通过穿透或散裂造成结构损坏,导致组件或子系统的潜在故障,最坏的情况是航天器完全毁坏或造成机组人员损失.
从历史上来看,1977年国际日地探测者(International Sun-Earth Explorer,ISEE 1)被微流星体穿透探测器窗口,造成低能宇宙射线探测器损坏,丢失了约25%的数据.1984年美国发射的长期暴露飞行器(Long Duration Exposure Facility, LDEF)在回收检查时发现有空间碎片和微流星体撞击形成的606个直径大于0.5mm的小坑[8].所以在设计航天器时必须考虑流星体环境.对于流星体撞击航天器的风险评估需要对流星体的通量、速度、密度和方向性进行描述,以计算穿透或撞击的概率.因此,一个有效的流星体模型必须准确地代表这四个方面的观测和测量结果.任何对在轨航天器的粒子撞击风险的评估都需要可靠的流星体环境模型.这些模型涵盖了从亚微米到厘米级的整个速度范围和颗粒直径和整个速度范围.航天器遇到的流星体环境由不同的统计模型指定.它们描述了流星体的空间分布,并提供了它们的碰撞通量、撞击速度和方向性的信息.
当前流星体环境模型主要包括质量密度模型和通量模型.
1.1 质量密度模型
零星流星体通常被认为起源于彗星和小行星,由于质量密度模型不是一个测量,流星体的密度存在严重的不确定性.根据雷达观测,其密度范围为:0.16g/cm3到4g/cm3.不同文献中引用的平均质量密度值差异很大,因此一般取0.5g/cm3作为估计.质量密度的关系为
(1)
其中,m表示流星体质量,单位为g.
1.2 流星体行星际通量模型
1.2.1 Grün模型
通量是用来表示在空间中单位时间撞击到航天器表面单位面积的物体数量.流星体环境通量模型目前较为通用,最早由Grün等[9]提出,该模型以积分的形式给出总平均流星体通量,即质量大于等于给定质量m每平方米每年的撞击粒子数.不考虑地球遮蔽和重力效应,这种模型的通量是全向的.适用于质量为10-18g到100g的流量体.其通量为
F(m)=3.15576×107[F1(m)+
F2(m)+F3(m)]
(2)
其中,
F1(m)=(2.2×103m0.306+15.0)-4.38
F2(m)=1.3×10-9(m+1011m2+
1027m4)-0.36
F3(m)=1.3×10-16(m+106m2)-0.85
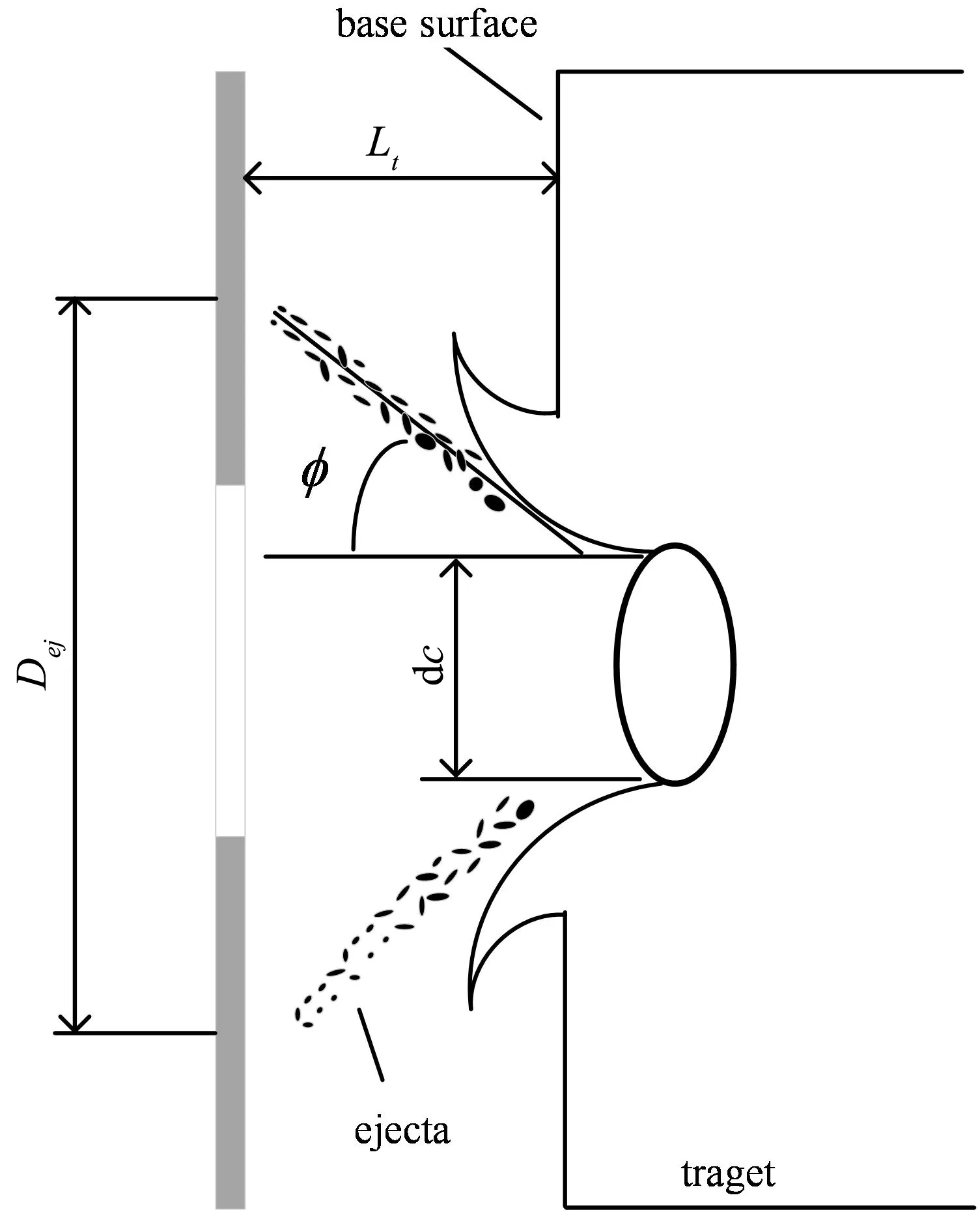
函数F1(m)对应质量m>10-9g的粒子,F2(m)对应质量10-14g Grün模型认为速度分布与撞击角度无关,该模型以解析的形式给出了太阳系1AU处地月轨道空间内的流星体通量,被广泛应用于地月轨道空间的航天器风险评估. 1.2.2 Divine模型 Divine模型是于20世纪90年代发展的流星体环境模型[10],该模型取日心黄道坐标系为参考坐标系,假设流星体仅在太阳引力作用下按轨道动力学规律运动,通过对观测数据进行分析获得流星体的质量分布函数、近地点分布函数、轨道倾角分布函数和偏心率分布函数,进而获得流星体的数目密度和通量.Divine模型可用于计算在太阳系0.1AU到20AU的行星空间内质量为10-18g到1 g的流星体通量,其最大的优点在于最早提出了非各向同性分布,即给出了流星体的速度分布,以确定流星体与航天器的相对速度.但该模型比较复杂,存在非线性计算问题. 1.2.3 Divine-Staubach模型 Staubach[11]改进了Divine模型,该模型利用了伽利略和尤利西斯尘埃探测器的测量数据验证了在波印廷-罗伯逊效应下演化小尘埃颗粒的长期动力学特性,并且添加了太阳光压作为第二扰动力,对原有模型进行了完善. 1.2.4 IMEM模型 Dikarev等人于2005年提出了行星际流星体工程模型IMEM(Interplanetary Meteoroid Engineering Model)[12-14],该模型除了将模型预测与观测相匹配外,还尝试根据影响流星体轨道和来源的物理效应构建流星体模型.模型中的行星际流星体群并非仅凭观测经验得出,而是来自许多主要的颗粒物的生成和动态分布的理论模型,同时模型补充了部分稀缺数据. 1.2.5 MEM模型 MEM(Meteoroid Engineering Model)模型[15]是基于加拿大流星轨道雷达数据,将流星体威胁范围定义在质量为10-6g到10g,以及距离太阳0.2AU到2AU的流星体.这是因为小于10-6g的颗粒不太可能穿透航天器,而质量大于10g的颗粒很稀少,不会构成威胁.建立MEM模型的目的是使航天器设计人员能够评估航天器被流星体撞击的可能性,预测撞击对航天器组件造成的损坏,并在必要时添加适当数量的流星体屏蔽.然而,MEM模型本身仅提供对流星体环境的描述,并不能预测航天器表明陨石坑或穿透的数量.NASA在MEM模型的基础上不断改进,2019年发布的MEM3模型包含了基于流星体消融模型的新流星体体积密度分布[16],同时修正了对流星体附近大质量物体影响的算法,校正了引力聚焦模型的同时,还保留了速度和方向性之间的所有相关性,提供了更准确的行星星历,MEM3还进行了多项性能改进.MEM3代码运行速度比前一代模型提速约3倍,提供了更多的用户帮助和更好的错误处理.最后,该代码现在支持跨平台:Mac 和 Windows 用户可以使用命令行版本.总之,MEM 3提供了更准确、更易于使用的太阳系内部流星体环境模型. 1.2.6 模型选用建议 随着空间微小物体动力学理论的发展以及计算机技术的进步,MEM3模型无疑是目前最先进、最便捷的流星体模型,其包含更广泛的数据来源,拥有更全面的模型动力学特性,同时软件具有更快的运行速度和更强的平台兼容性. 碎片模型主要包括几类:解体模型、碰撞溅射模型、碎片总量预报模型、碎片受力模型与碎片通量计算模型.空间碎片事件发生与模型的关系可以用图1来表示. 图1 空间碎片事件与模型关系示意图 解体模型主要描述了太空物体碰撞后产生碎片大小、速度的分布情况.解体模型常用NASA标准解体模型[17],NASA标准解体模型将碰撞引起的解体事件分为灾难性碰撞解体和非灾难性碰撞解体两种,该模型中引入了“动能质量比”来区分碰撞类型,动能质量比即较小碎片的相对动能(相对动能是指计算动能的过程中速度用相对撞击速度)除以较大碎片的质量.公式如下: (3) 动能质量比以40 J/g为限, 若大于或等于40 J/g, 则发生灾难性碰撞;若小于40 J/g, 则发生非灾难性碰撞.解体后对于碰撞碎片的分布可以用质量或特征长度来描述. NASA标准解体模型对于计算大于等于给定尺寸碎片的数量为 N(LC)=0.1(M)0.75(LC)-1.71 (4) 对于特征长度小于8cm的物体,由超高速碰撞产生碎片的面质比为 (5) 其中,λC=lgLC,χ=lgA/M.N表示均值为μSOC(λC),标准差为σSOC(λC)的正态分布.设速度增量为ΔV,取其对数表示ν=lgΔV,则速度增量符合正态分布 DΔV(χ,ν)=N[ν;μ(χ),σ(χ)] (6) 均值为μ(χ)=0.9χ+2.9 标准差为σ(χ)=0.4 碰撞溅射模型主要描述了碎片在撞击航天器金属表面时,所产生的坑的深度、直径以及溅射角.碰撞溅射模型可以帮助地面分析在太空中发生碰撞时,碎片对航天器的损伤程度,以便设计更加完善的碰撞保护装置或在碰撞后采取合理的后续措施.Whipple保护层是用于防御微流星体和空间碎片破碎的标准设备,由放置在航天器内部结构壁外侧的薄金属板组成,由Whipple于1947年首次提出[18],用于抵御空间微流星体对航天器的撞击.自20世纪60年代以来,研究人员们设计了许多薄板射孔方程,用于计算碎片撞击到航天器金属表面形成的穿孔大小以及弹孔深度等.Hayashida和Robinson[19]回顾了为航天器屏蔽开发的单壁穿透中使用的一些最常见的弹道极限方程.Herrmann和Wilbeck[20]对穿透理论进行了更全面的回顾,Hill[21]提出了薄板的射孔预测方程.目前常用单壁穿孔模型为Charters模型[22],目标形变应力为 (7) 其中,D表示撞击穿透深度,m表示撞击碎片的质量,v表示传入撞击速度.对于给定球形碎片,将其质量转换为密度与碎片直径的函数,碎片密度表示为ρd,撞击穿透深度可以表示为 (8) Charters和Summers根据公式 (8) 推导了Ames 方程,表示为 其中,H为公式 (8) 中D的2倍,c表示被撞击体的纵波速度,ρt表示被撞击体材料密度. 1998年Burchell等[23]通过实验对撞击直径计算公式进行了修正 (9) 其中,d表示弹丸直径,单位厘米,H表示弹丸硬度,用Brinnell数值表示,V表示相对撞击速度,单位km/s;Cs表示声波在被撞击目标材料中的传播速度;θ表示碰撞相对于法向夹角. 当发生未穿透超高速碰撞时,Nishida等人对碰撞产生的撞击坑及碰撞溅射物角度进行了实验分析,溅射物最大溅射角为[24] (10) 其中,Dej表示溅射物喷溅外环直径,dc表示形成的撞击坑直径,Lt表示外层检测板与被撞击目标物距离.图2与图3形象地表示了喷溅实验各测量值之间的关系. 图2 检测板示意图 图3 溅射实验示意图 2013年Lamberson[25]修正了Charters模型,用于计算撞击坑大小.在撞击时发生断裂的位置通常被称为Hugoniot弹性极限,其计算方法为 (11) 其中,Y表示屈服应力,v表示泊松比,一般在断裂处,平均压力的增加具有最大剪切应力.则根据σHEL计算修正的撞击穿孔直径为 (12) 碎片总量预报模型主要描述了随着时间的推移,在整个太空环境中,碎片总量的变化情况. 尽管目前太空中的大部分碎片都由爆炸产生,但许多模型预测,即使在未来没有任何发射的情况下,碰撞也会带来更多的碎片[26-27].对未来空间碎片的总量进行估计有助于地面更好地安排发射任务,以躲避已经产生的空间碎片.但是由于未来空间活动的不确定性和构成代码算法的概率性质,可靠的统计数据只能从使用蒙特卡罗方法数十甚至数百个单独的模拟中得出.在对LEO碎片环境历史演变的研究中[28],碰撞活动的间歇性、随机爆发导致单独的模拟,其中没有两个结果是相同的,即使采用相同的历史发射活动也是如此.因此,使用这些代码预测未来碎片环境的过程是一项耗时且计算成本高的任务. 2.3.1 PIB模型 PIB(Particles-In-a-Box Model)模型是由Talent于1992年提出[29],该模型不需要计算机密集型蒙特卡罗模拟来预测不断变化的碎片环境的总体特征,而是使用微分方程描述.该方程允许通过对方程系数的直接分析来测试LEO环境的稳定性.根据PIB模型,空间物体数量的变化率为 (13) 其中,A,B,C是与LEO环境有关的物理性质,A为沉积系数,B为去除系数,C为碰撞系数,N为空间中物体个数.使用这种方法预测未来低地球轨道碎片环境的计算成本非常低,因此,它可用于快速评估各种情景.虽然该方法仅限于可以分析的一小组状态(物体数量、总质量和平均物体半径),但当考虑碰撞防御时,这些状态通常与更复杂的大规模计算结果具有高度重合性. 2.3.2 FADE模型 FADE(Fast Debris Evolution)模型[30]采用一阶微分方程来描述尺寸大于10cm的LEO新物体从环境中添加和移除的速率.FADE模型已被实现为客户端、基于Web的服务,使用嵌入在HTML文档中的JavaScript服务.由于算法的简单性,FADE可以立即以图形格式提供未来预测的结果,用户可以完全控制关键模拟参数.对于尺寸大于或等于10cm的LEO碎片环境,模型可以在各种不同情景下对历史和未来环境进行预测,包括一切如之前任务的情形,未来不发射,任务后处置和修复.此外,模型的计算速度和灵活性使用户能够探索和了解空间碎片环境的演变. 在PIB模型中,碎片群的运动被假设为随机运动,同时定义了一种“不完全混合因子”来中和这种假设带来的负面影响,而在FADE模型中,模型同样做了这样的假设,但是假设的前提是碎片碰撞率的产生是通过地球同步碎片环境分析与监测模型计算得到,以此来确定FADE模型中相关量的系数.FADE模型相关计算公式为 (14) 其他相应数值可以用下式计算 2.3.3 LEGEND模型 LEGEND(LEO to GEO Environment Debris Model)模型[31]是一个全尺寸、三维、碎片演化模型,是美国宇航局轨道碎片计划办公室用于研究长期碎片环境预测的主要模型.它覆盖高度在200~50000千米之间的近地空间,包括LEO、MEO以及GEO区域.LEGEND模型利用蒙特卡洛方法模拟,重复1996年至2003年的发射,并对未来100年的空间碎片总量进行了预测.LEGEND模型分析表明,未来几乎所有的碰撞均发生在LEO.而大部分发生在LEO的碰撞集中在约800~1000千米的高度,约一半以上的碰撞的速度大于14 km/s.同时,LEGEND模型还可以用来解决可能有哪些物体参与碰撞(完整体与完整体的碰撞、碎片与完整体的碰撞、碎片与碎片的碰撞),碰撞是否有倾向性和依赖性,并模拟未来碎片环境的演变. 根据LEGEND模型描述,在给定一段长时间t0到tf内,物体i和物体j的碰撞次数可以表示为 (15) 其中,Pi,j表示碰撞概率,L表示将整个时间划分的时间间隔数量,ts和ts+1表示给定时间间隔s内的起始时间和结束时间.在对碰撞概率进行计算时,模型假设在给定的时间对空间进行快照,只有在一个小体积内的两个元素才可能发生碰撞,快照将空间分成若干个立方体,只有当两个物体出现在同一立方体内时,才有可能发生上述碰撞,此时碰撞概率为 Pi,j=sisjVimpσdU (16) 其中,si和sj为立方体中物体i和j的空间密度,Vimp表示两个物体的相对速度,σ表示碰撞横截面积,dU是立方体的体积.式(16)是基于Kessler[32]开发的相同空间密度方法,在微观尺度上,应用空气动力学理论来评估碰撞概率. 碎片受力模型主要描述了碎片在太空运行过程中的受力分析及轨道变化.碎片受力情况的分析是碎片空间运动与演化的基础.地球附近的碎片的运动方程可以表示为 fA+fs+fP+fL+fM+fSR+fPR+fPD (17) 2.5.1 MASTER模型 MASTER-2009(Meteoroid and Space Debris Terrestrial Environment Reference Model)模型最早由布伦瑞克工业大学与欧洲航天局(ESA)联合开发[34],该模型可以对从LEO到高度略高于GEO的所有空间碎片通量进行预测.模型对太空飞行事件中的每一次碎片事件都进行了模拟,生成的碎片云包含所有直径大于1μm的颗粒,并且对所有碎片轨道都进行了计算.MASTER-2009有几方面优点:首先该模型着重考虑高轨摄动理论对碎片群形状和方向变化带来的影响;其次,该模型基本考虑了所有产生碎片的来源,包括航天器爆炸或碰撞产生的碎片,火箭发动机不完全燃烧的炉渣颗粒,星载冷却系统释放的液态金属液滴,以及LEO上较小的空间物体或微流星体产生的微小物体;同时,该模型在一直使用测量数据和新发现的碎片来验证模型模拟的碎片环境,以便不断对模型进行修正.模型发现目前航天器发生最高碰撞风险的轨道高度在800~900千米.而800千米的轨道高度通常对应太阳同步轨道,对于地球表面观测任务十分重要,故该结论值得高度重视.MASTER-2009同时支持根据历史发射数据和预先定义的发射率来预测未来至2060年太空碎片的演变过程[35]. ESA后来在MASTER-2009的基础上又发布了MASTER 8模型,该模型对空间环境进行了改进,并且在最后的预测结果中加入了预测不确定性[36]. 2.5.2 ORDEM模型 ORDEM(Orbital Debris Engineering Model)模型由NASA轨道碎片计划局开发,最新版本为ORDEM 3.1,该模型使用与 2013 年发布的前身 ORDEM 3.0 相同的模型框架.该模型适用于需要对空间碎片环境(碎片空间密度、通量等)进行概括和估计的工程解决方案,通过碎片材料密度对碎片进行分类[37].ORDEM 3.1还可用作地面碎片测量和观测的基准,模型结合了最新的高保真数据集,如Fengyun-1C、Iridium 33和Cosmos 2251碎片云数据以及先进的数据分析技术来构建和验证包含从2016年至2050年LEO到GEO的计算结果.ORDEM 3.1中包含大量反映当前碎片环境的观测数据.该数据涵盖了10μm到1m的物体尺寸范围.同时,对于之前各类模型没有观测GEO区域1m以下尺寸碎片的能力进行了弥补,将对GEO区域碎片研究能力精确到10cm尺寸量级. 2.5.3 通量模型选用建议 NASA 的 ORDEM和 ESA 的 MASTER这两个主要轨道碎片工程模型自建立以来都取得了重大进展,现在代表了各自机构在空间碎片方面的最先进水平.MASTER对碎片的通量分析主要以火箭发动机燃料残渣、爆炸和碰撞产生的碎片作为碎片源,而ORDEM对碎片的分析则以碎片密度为主要指标.MASTER的分析时间跨度为1957年至2060年,要比ORDEM的2010年至2035年跨度更大,而且MASTER的分析时间间隔可以设置为任意间隔,而ORDEM的时间间隔只能为1年的整数倍.显然MASTER要更加灵活.在结果的对比上,两种模型在GEO轨道的通量计算上基本匹配,但是在如空间站轨道、GTO轨道,两者还是在某些不同尺寸的空间碎片通量预测中有差异,两者在未来也会加强合作,构建更加精准的通量模型.总体而言,目前这两种模型都代表了国际最先进的水平. 轨道空间日益增多的微流星体与空间碎片对人类的太空活动构成了严重威胁,建立完备的流星体与碎片模型可以为航天任务事前分析与安全稳定运行提供有力保障.本文回顾了流星体与碎片模型发展的重点事件,详述了流星体模型中的质量密度模型与通量模型,并给出了针对流星体模型的选用建议.同时,对从空间事件碎片产生到未来空间碎片总量的预测,以及不同模型的使用规则与适用范围进行了深入讨论,给出了不同模型目前最先进的模型对比与总结.目前主流的无论是解体模型还是通量模型,其根基与发展都在国外,国内对此方面的研究与国际上仍存在差距,未来我国的空间活动必将逐渐增多,构建一套我国官方的流星体与空间碎片系列模型以支撑太空交通管理将是必然趋势.2 碎片模型

2.1 碎片解体模型
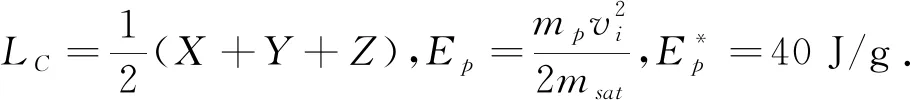
2.2 碰撞溅射模型

2.3 碎片总量预报模型

2.4 碎片受力模型


2.5 碎片通量模型
3 结论

