水压马达配流副椭圆形织构表面流场分析*

赵 涛 王优强 胡 宇 何 彦 李梦杰 朱玉玲

(1.青岛理工大学机械与汽车工程学院 山东青岛 266520；2.工业流体节能与污染控制教育部重点实验室 山东青岛 266520)

进入21世纪，全球海洋事业迅速发展，海洋资源的开发利用成为了世界经济增长的一大支柱。海水液压马达作为海洋探索的重要执行元件有着极其重要的作用。然而，由于海水特殊的物理化学性质，海水液压马达中的关键摩擦副之一——端面配流副在海水中工作时极易因腐蚀、磨损而失效[1]。目前，国内外学者主要通过采用新材料[2-3]、改变润滑方式[4-5]、进行涂层防护[6-7]等方法提高其摩擦学性能。随着表面织构技术的发展，利用织构表面效应来进一步提高摩擦副的摩擦磨损性能有很大的潜力。

表面织构被认为是提高摩擦副表面摩擦学性能的有效方法之一。JONES和SCHMID[8]通过高频率循环摩擦磨损实验得到织构化表面的磨损性能明显优于光滑表面的结论。WAKUDA等[9]通过销盘实验模拟了具有很高接触压力的圆柱/平面接触界面，研究发现织构化陶瓷摩擦副表面的摩擦特性与微坑大小和密度有很大关系，密度为5%～20%的微坑表面减摩效果最好。LIU等[10]通过数值模拟和实验研究的方法，发现织构的几何参数对摩擦副表面的摩擦学性能有显著影响，最优几何参数取决于其所处的操作条件。袁明超[11]通过正交试验分析了表面织构的不同参数对活塞环/缸套摩擦副摩擦学性能的影响，得出凹坑的直径对摩擦副摩擦因数的影响最为显著，当速度与载荷较高时，表面织构作用明显。SAEIDI等[12-13]研究了不同工况下织构的不同参数对摩擦副摩擦学性能的影响，结果表明，织构直径和面积率对摩擦因数的影响较大。GALDA等[14]研究了乏油条件下速度和载荷对织构化表面的影响，发现在低速低载条件下，织构的作用效果更明显。

近年来，部分学者对海水液压马达关键部件进行摩擦学研究，探索织构化表面对其减摩抗磨性能的影响。梁瑛娜等[15-16]利用FLUENT仿真分析非光滑表面滑靴副的流体动压支撑效应，并通过自制的试验台对加有织构的滑靴副进行了摩擦磨损测试，结果表明：织构能够产生良好的动压润滑效应，织构的存在可以使润滑液和磨屑存储在其中，降低磨粒磨损，加工有织构的摩擦副的摩擦因数和磨损率相较于光滑表面均大幅降低。孙怡龙等[17]利用ANSYS 软件，分析了不同密度及不同深径比凹坑对双织构(上圆柱下圆锥)低速大扭矩水液压马达配流副等效摩擦应力的影响，发现织构化表面可以减小应力集中，有效降低摩擦副表面最大等效摩擦应力。WANG等[18]通过在CFRPEEK试样上加工圆球形、椭球形和三棱柱型仿生织构，与光滑试样进行摩擦磨损实验对比，发现合适的非光滑表面能够有效地降低摩擦副的摩擦因数，其中，椭球形织构的摩擦性能最好。马浩等人[19-20]通过对比不同形状的织构化配流副表面，发现圆形织构具有最好的流体动压润滑性能。但目前为止，很少有学者探究同一织构的不同参数对海水液压马达配流副润滑性能的影响规律。

本文作者利用FLUENT软件，在不同转速、不同面积率下对不同直径的椭圆形织构进行仿真分析，探究其影响规律，为加工织构化配流副表面提供理论依据。

1 仿真模型的建立

1.1 表面织构几何模型及FLUENT模型选择

文中根据WANG等[18]和YU等[21]的研究成果，选择润滑效果最好的垂直于滑动方向的椭圆形织构布置在配流副表面；同时为节省运算时间、提高精度，故选取配流副的一个具有表面织构的圆环单元进行计算，如图1(a)所示，圆环单元尺寸如图1(b)所示。

定义凹坑总面积与单元圆环总面积的比值为凹坑面积占有率A，则

式中：a、b分别为椭圆的短半轴长、长半轴长，mm；x为凹坑数量；R、r分别为圆环单元模型的外、内半径，mm。

XU等[22]通过研究发现，长短轴比为2∶1的椭圆形织构能有效地减摩抗磨，而过大的长短轴比则会加剧磨损。故文中选取椭圆形织构的长短轴比为2∶1。文中设计3种不同尺寸的椭圆形织构，其长短轴分别是1.6、0.8 mm，1.2、0.6 mm和0.8、0.4 mm，在文中表示为1.6/0.8、1.2/0.6、0.8/0.4 mm；织构面积率分别是5%、8%、10%、13%、18%、21%；织构深度保持不变，为0.4 mm。

文中主要研究海水润滑下织构化配流副表面的流体动压效应，故采用不可压缩流体、定常、湍流模型进行分析。湍流模型选用旋转流动分析性能更好的Realizablek-ε模型。工作介质为海水，其密度为1 025 kg/m3，动力黏度为1.037×10-3Pa·s。

1.2 网格划分及无关性验证

网格质量的好坏会影响仿真分析结果，合适的网格能加快计算收敛速度，提高运算精度。文中利用ANSYS自带的Mesh模块对水膜单元模型进行四面体网格划分，求解偏好为CFD Fluent，运用能够较好捕捉曲率变化的Curvature法，关联度采用Medium，跨度中心角设置为Fine。文中模型的网格质量系数的平均值约为0.75，偏斜系数的平均值约为0.27，配流盘水膜单元模型及网格划分如图2(a)、(b)所示。在保证计算精度同时，为减少计算时间，文中以1.2/0.8 mm的椭圆形织构水膜为例进行网格无关性验证，如图3所示。随着单元总数的减小，水膜上表面最大压力基本保持不变，网格质量随单元总数的减小也基本趋于平缓。根据验证结果，整个计算模型的单元总数取1 764 315个，即对应的网格尺寸为0.03 mm。

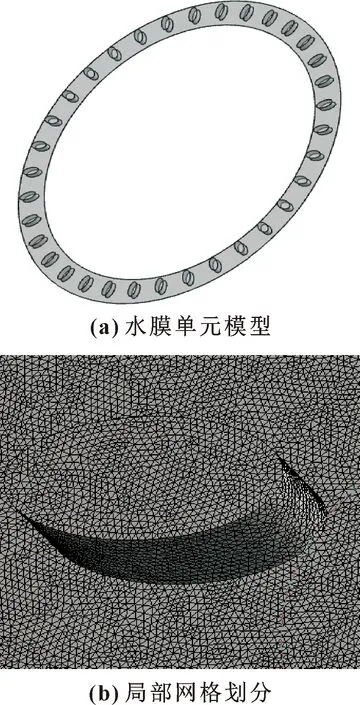
图2 配流盘水膜模型及局部网格划分

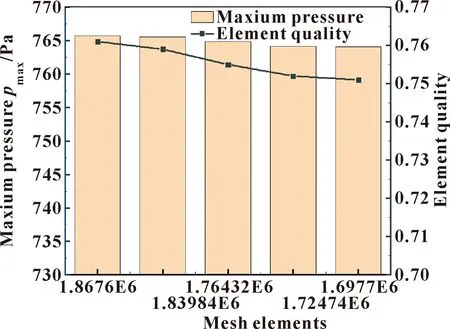
图3 无关性验证

1.3 边界条件及计算参数的设置

边界条件设置如图4所示:与转子相接触的表面设置为动面，且沿主轴做逆时针匀速圆周运动，取主轴转速分别为500、1 500、2 500 r/min；固定壁面设置为与配流副表面相接触的表面，圆环内表面设置为压力入口边界，圆环外表面设置为压力出口边界，取进出口压力均为0。采用 SIMPLEC 算法进行求解，压力项选用Body Force Weighted，其余项均选用Second Order Upwind。

图4 边界条件

2 结果分析与讨论

2.1 计算模型有效性验证

为保证计算模型的有效性，设定模型几何参数、控制方程、边界条件及网格划分方法与文献[15]保持一致，但设定其工作条件与文中保持一致。如图5所示为文中模型与文献[15]中模型的压力对比情况，文中压力变化趋势与文献[15]中压力变化趋势基本一致，表明文中采用的计算模型和计算方法较为合理。

图5 文中方法计算结果与文献[15]结果对比

2.2 水膜上表面压力分布

为探究椭圆形织构表面的水膜承载特性，取转速为2 500 r/min，面积率为13%的3种不同尺寸的椭圆形织构进行了分析，其二维压力云图、三维压力山峰图如图6所示。设定摩擦副绕轴线顺时针旋转，由图6(a)、(c)、(e)可知，沿顺时针方向，凹坑处的水膜压力呈现出先减小后增大的现象，最小负压出现在凹坑中心偏后位置，最大正压出现在凹坑边缘。结合三维压力山峰图，可以发现最大负压均小于最大正压，织构化水膜的整体压力为正，即不同尺寸的椭圆形凹坑均能产生良好的水膜承载力。凹坑处水膜压力先减小后增大的原因是加工在摩擦副表面的椭圆形织构在液体流动过程中会形成微小的收敛楔和发散楔[23]，水在流经凹坑时，凹坑的前缘会产生发散楔，导致水膜压力下降，而水在流过凹坑时，凹坑后缘会形成收敛楔，水膜压力急剧升高。

图6 不同尺寸的椭圆形凹坑的压力云图和压力山峰图

2.3 面积率及转速对不同尺寸椭圆形织构的影响

图7所示为不同尺寸椭圆形织构在不同转速下的平均水膜压力随面积率的变化情况。可知，在相同面积率下，3种不同尺寸织构的水膜压力都随转速的增大而增大，这是因为水膜总压由动压和静压组成且由动压主导[15]。动压的表达式为ρv2/2。随着转速的不断增大，动压也随之增大，从而导致总压增大。对比3种不同尺寸织构的压力曲线，相同尺寸的椭圆形织构在不同转速下其水膜压力随面积率的变化呈现出相同的变化规律，并且，转速越大，变化越显著。另外，不同尺寸椭圆形织构的水膜压力随面积率的变化呈现出不同的变化规律。其中，尺寸为0.8/0.4、1.6/0.8 mm的椭圆形织构的水膜压力随面积率的变化总体呈现出先增大后减小的趋势，其最优面积率分别为13%和18%；而1.2/0.6 mm的椭圆形织构总体呈现出不断增大的变化趋势，其最优面积率为21%。通过对比3种尺寸的椭圆形凹坑，可以发现随着织构尺寸的不断增大，椭圆形织构的最优面积率的变化趋势为先增大后减小。

图7 不同尺寸椭圆形织构在不同转速下水膜压力随转速的变化

针对以上变化规律，文中以直径为0.8/0.4 mm的椭圆形织构为例，分析得到面积率为8%、13%和21%的织构化表面的单个凹坑内的流迹线和压力曲线，如图8所示。随着面积率的增大，凹坑内已成核涡旋先向右上移动再回落，在凹坑面积率为13%时，涡旋离摩擦副上壁面最近，产生的流体动压效应最强。通过对比压力曲线图，面积率为8%的凹坑在89°～90.5°的低压区的压力波动范围较大，能量损失大，故其整体水膜支撑力最小；而面积率为13%和18%的凹坑在此范围内的压力集中在-200 Pa左右，但面积率为18%的凹坑水膜压力波动较面积率为13%的凹坑的水膜压力波动大；另外，面积率的增大导致织构间距不断减小，当织构间距过小时，相邻织构的发散楔和收敛楔相互影响显著，即前一个凹坑的收敛区与后一个凹坑的发散区部分抵消[24]，故而，面积率为18%的织构表面凹坑内的高压区不及面积率为13%的织构表面。综上所述，面积率为13%的织构表面整体水膜支撑力最大，面积率为18%的织构次之。

由以上分析可知，直径为0.8/0.4、1.2/0.6和1.6/0.8 mm的椭圆形织构的最优面积率分别是13%、21%和18%，在此基础上，文中进一步探究不同直径的椭圆形织构在各自最优面积率下的最大水膜压力随转速的变化，如图9所示。3种不同直径椭圆形织构的水膜压力都随转速的增大而增大，其中直径为1.6/0.8 mm的椭圆形织构表面水膜压力最高，直径为1.2/0.6 mm的椭圆形织构表面水膜压力次之；直径为0.8/0.4 mm的椭圆形织构表面水膜压力最低。

图9 不同尺寸织构表面最大水膜压力随转速的变化

图10所示为2 000 r/min下不同直径椭圆形凹坑的流迹线和速度梯度。对比图10(a)、 (c)和(e)，可以发现凹坑的右上角存在一个成形的涡旋，随着凹坑直径的不断增大，成形涡旋不断向收敛楔方向移动；而在凹坑的左下角逐渐形成一个小涡旋。结合图10(b)、(d)和(f)，随着凹坑直径的增大，右上角的涡旋体积不断减小，流体动能转换成漩涡能量的效应减弱，水膜压力上升，且凹坑的左下角在涡旋形成的过程中，速度梯度变化更加紧密，流体动压效应愈加明显；另外，凹坑尺寸的增大使撞击凹坑底部的水流束更加集中，产生更大的回流冲击效应。通过以上各点的综合作用，使得在一定范围内，凹坑尺寸越大，水膜压力越高。

图10 2 000 r/min下不同直径凹坑的流迹线和速度梯度

3 结论

建立椭圆形织构液压马达配流副表面模型，分析织构参数对水膜承载性能的影响，仿真结果表明：

(1)不同尺寸的椭圆形织构均能产生良好的水膜承载力，其水膜承载力随面积率的变化呈现出不同的变化规律，但相同尺寸的椭圆形织构随面积率的变化呈现出相同的变化规律，在实际应用中应根据不同的织构尺寸选择不同的面积率。

(2)在相同面积率下，转速越高，织构的水膜承载力越强，故在高转速配流副中，织构能够产生更好的承载效果。

(3)通过对比不同尺寸的椭圆形织构在各自最优面积率下对水膜承载力的影响，无论在多大转速下，1.6/0.8 mm的椭圆形织构能表现出较优的水膜承载性能。