基于CFD数值模拟的异面三通管冲蚀磨损规律研究*
莫 丽 刘 栖 许先雨
(西南石油大学机电工程学院 四川成都 610500)
管道运输作为目前最主要的油气运输方式,具有安全、运输量大、耗能小且能够连续工作等优点[1]。随着人们近年来对石油与天然气的需求日益升高,使得管道的发展与应用得到了广泛的关注。然而管道在石油与天然气运输中的局限性也显而易见,即流体中的微小固态颗粒对管壁的冲蚀磨损易导致管道失效。一旦管道失效破坏,不仅需要高昂的检测与维修费用,还会造成生态环境的污染[2-3]。因此,针对管道失效机制的研究,对于延长管道寿命具有积极的意义。
祝效华等[4]在控制单因素变量的条件下研究了三通方位夹角、压裂液流量、颗粒体积分数、颗粒直径和压裂液密度对三通冲蚀磨损的影响规律。陈宇和马贵阳[5]研究了不同流速、颗粒直径、质量流量等因素对管道冲蚀的影响,对三通管的冲蚀磨损进行了预测。张孟昀等[6]利用DPM模型,通过CFD仿真分析对比了盲管与弯管的冲蚀机制。李介普[7]对油气管线中的弯头、盲通接头和异径管进行了冲蚀磨损数值计算,指出盲三通接头管道交汇处最容易发生冲蚀破坏,为冲蚀检测提供准确的测量点位置。王凯等人[8]研究了颗粒轨迹与Stokes数在拉格朗日坐标系下对弯管冲蚀位置的影响规律。MENG和LUDEMA[9]对影响颗粒冲蚀的因素进行了归纳总结,发现颗粒浓度、撞击速度和角度、颗粒的形状、硬度和直径、管壁的硬度等都会对冲蚀作用产生影响。BLANCHARD等[10]利用管流冲蚀试验方法研究了弯管弯径比和颗粒直径对管壁冲蚀磨损的影响,结果表明,弯头最严重的冲蚀部位基本上不会随着颗粒直径与弯头材质的变化而改变。
异面三通管是油气管线中的重要组成部分,在实际工程中应用较为广泛,由于其几何形状与受载情况较为复杂,目前对于失效率较高的异面三通管的冲蚀规律研究还不够完善。为了更全面地评估异面三通管的耐冲蚀性能,预测其冲蚀分布,本文作者采用CFD仿真模拟的方法,在前人研究的流体流量、颗粒直径、含砂体积比的基础上,开展异面方位夹角等因素对该种管道冲蚀磨损性能影响的评价分析。
1 理论模型
1.1 湍流模型
湍流是工程技术领域中一种常见的非常定三维随机流体运动现象。计算异面三通管中流动的雷诺数,可得知其为湍流,故选择标准双方程k-ε湍流模型,其具有精度较高、使用范围较广、能够计算完全湍流的管流流动等特点[11]。标准双方程k-ε湍流模型如下:
(1)
(2)
式中:k为湍动能,J;ε为湍动能耗散率;σk和σε分别为湍动能k和耗散率ε对应的Prandtl数;经验常数C1ε、C2ε的取值分别为C1ε=1.44,C2ε=1.92;Gk是平均速度梯度引起的湍动能产生项。
1.2 壁面碰撞恢复方程
由于颗粒与管道壁面发生碰撞时会存在能量损失,因此反弹速度低于入射速度。颗粒-壁面模型在CFD冲蚀分析中,常用来求解反弹颗粒的速度变化,该模型需要定义2个重要的恢复系数,分别为法向分量en和切向分量eτ,其表达式为
(3)
因为油气管道材质主要为碳钢,故采用能够有效表征颗粒碰撞壁面后速度特性的Tabakoff模型[12],其表达式为
en=0.993-0.030 7θ+4.75×10-4θ2-2.61×10-6θ3
(4)
eτ=0.988-0.029θ+6.43×10-4θ2-3.56×
10-6θ3
(5)
1.3 冲蚀模型
对于管道内湍流的冲蚀预测,文中选用Fluent中提供的DPM离散相模型作为计算的冲蚀模型。冲蚀速率公式为
(6)
式中:mp是颗粒质量流量,kg/s;C(dp)为颗粒的粒径函数,为1.8×10-9;α为颗粒路径与壁面间冲击角;f(α)为冲击角函数,当α为0°、20°、30°、45°与90°时,f(α)分别为0、0.8、1.0、0.5与0.4;v为颗粒相对速度;b(v)为颗粒相对速度vp的函数,为0;Aface为壁面面积,m2。
2 建立模型、网格划分与边界条件设置
文中所研究的异面三通管由位于水平面的流体出口管段b、c和异面流体入口管段a组成,3根管道的直径D与长度L均相同,取D=70 mm,足够长的管道才能保证离散相与连续相充分流动,故取L=10D。流体出口管段b、c由一90°弯头相连,弯曲半径R=1.2D,a管轴线在b、c管平面的投影与b、c管两轴线的等分线重合,且a管轴线与b、c管两轴线等分线的夹角为α。图1为异面三通管结构示意图。
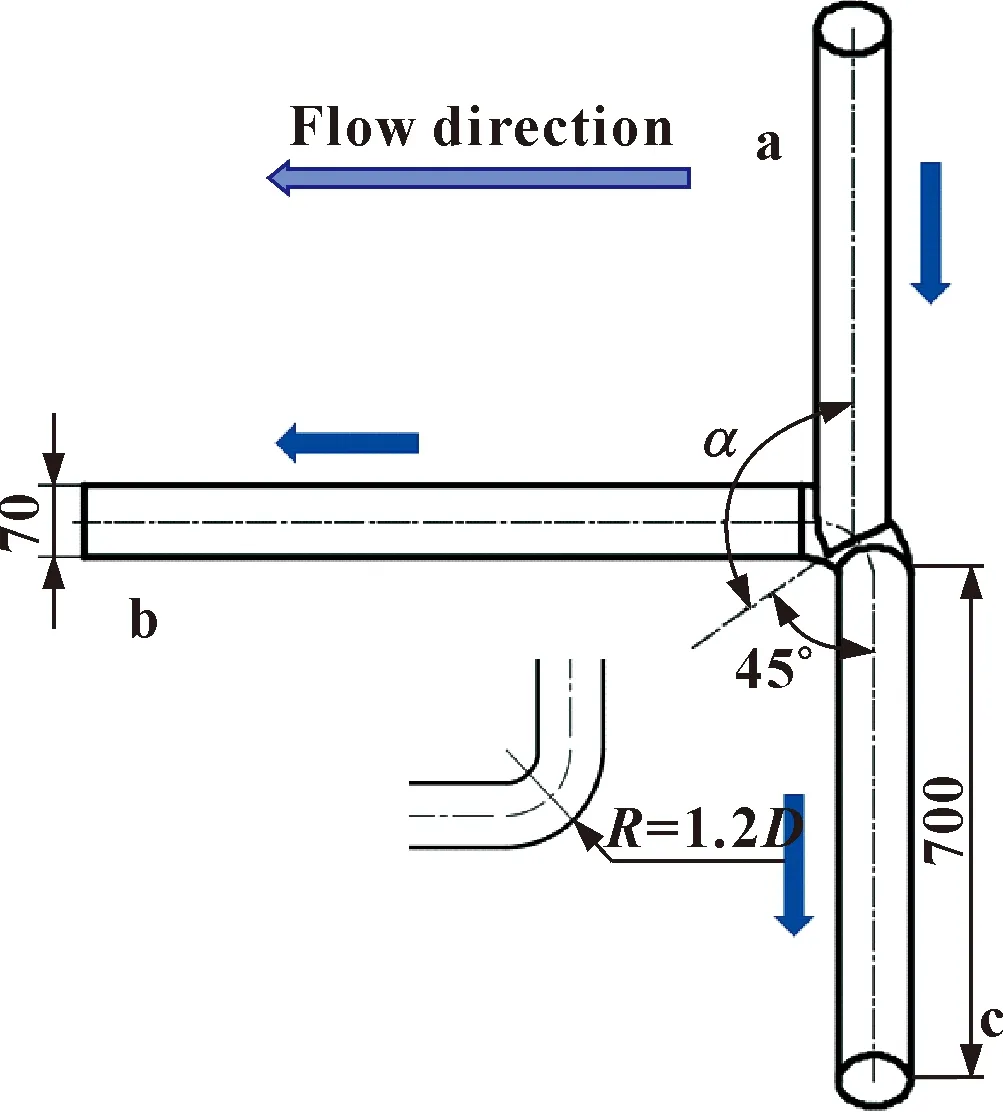
图1 管道结构示意
对模型进行网格划分,划分方法采用非结构化网格;对弯头处进行网格局部加密,并在近壁面添加边界层网格,层数为5,划分方式采用First Layer Thickness。网格模型如图2所示。当三通管网格数量取220 974时,网格数量对仿真结果影响较小,因此认为网格满足无关性要求。
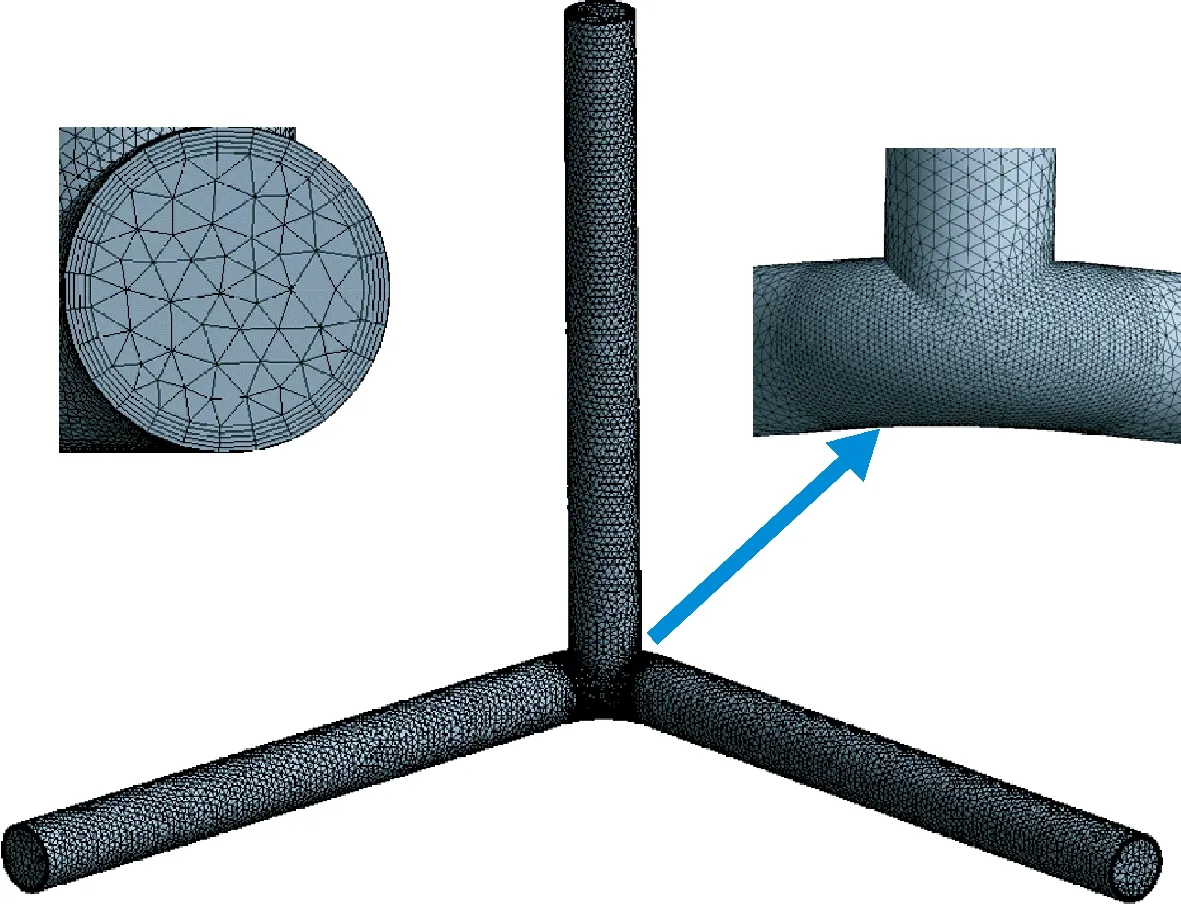
图2 网格模型
文中模拟仿真中的离散相为砂粒,密度为2 800 kg/m3,连续相为油品,密度为960 kg/m3;入口边界条件采用速度入口,出口边界条件采用自由流出;砂粒与油品速度一致;动量、流体扩散率和湍动能采用二阶迎风离散格式;求解器选择半隐式SIMPLE算法。
3 结果及讨论
深入研究异面三通管冲蚀磨损规律,对管道结构优化与安全评估有十分重要的意义。文中在单一变量的原则下,分析了流体速度、含砂体积比、异面管夹角与砂粒直径对异面三通管最大冲蚀速率的影响。
3.1 流体速度对冲蚀率的影响
选取砂粒直径d=0.1 mm,含砂比φ=2%(体积分数,下同),在异面管夹角α分别为90°、120°、150°条件下,计算分析流体流速(2~10 m/s)对管道冲蚀磨损的影响。
图3所示为流体流速对管道最大冲蚀率的影响。可知,管道的最大冲蚀速率与流体流速呈指数型正相关。流速较低时,流体对颗粒携带性不够,固体颗粒动能不足,在碰撞过程中相对分散,故冲蚀效率低;当流速较高时,造成的冲蚀损伤远高于低流速下,这是由于固体颗粒的撞击动能与速度呈2次方关系,固体动能随着流体湍动能增大而大大上升[12]。此外,随着流速的增大,当异面管道夹角越大,其冲蚀率的增幅减缓,这是由于夹角的增大,管道对固体颗粒的流动约束减小,颗粒与管壁的碰撞频率降低。
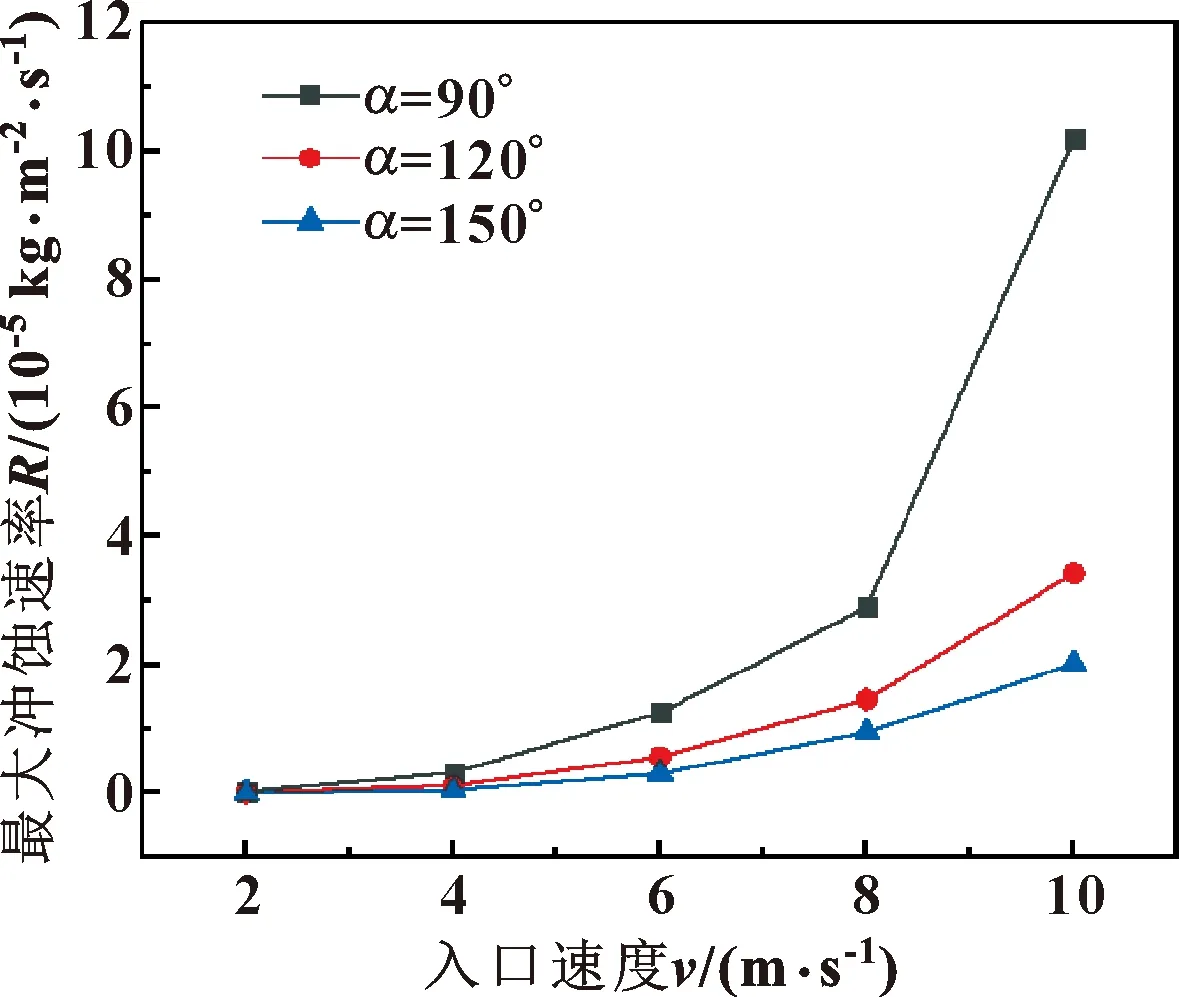
图3 不同异面管夹角下流速对冲蚀磨损的影响
图4所示为异面管夹角120°条件下,三通管在不同流速下的冲蚀磨损云图。如图所示,随着流体速度由低到高,管道的冲蚀率与冲蚀区域逐渐增大,b、c两管弯头上侧管壁处是受损最为严重的部位,这是因为该部位对流体的运动有阻挡,固体颗粒经过时发生偏向,造成与管壁碰撞的颗粒数增多,故冲蚀程度最为严重。
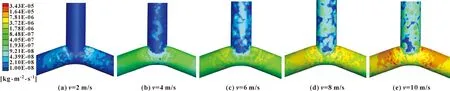
图4 不同流速下冲蚀磨损云图
3.2 含砂体积比对冲蚀率的影响
流体的含砂体积分数φ为影响管道冲蚀磨损的重要因素之一,故选取砂粒直径d=0.1 mm,流体速度分别为2、6、10 m/s,异面管夹角α为120°的条件下,开展在1%~9%含砂体积分数下管道冲蚀磨损研究。
图5所示为不同流速下含砂体积比对管道冲蚀磨损的影响。可以看出,随着固体颗粒体积分数的增加,管道的最大冲蚀率近似呈线性增长,其增长幅度小于流速变化条件下的指数型增长,说明含砂体积比对管道冲蚀率的影响要小于速度对其的影响。分析冲蚀机制:流体流速较低时,其对颗粒携带性不足,颗粒动能较低,与壁面冲击次数减小,因此低流速条件下,冲蚀率并没有随着含砂体积比的增大而发生明显升高;流体流速较高时,砂粒体积分数的增大加大了与壁面碰撞的概率,造成管道冲蚀磨损的加剧,导致了更严重的冲蚀结果[13]。
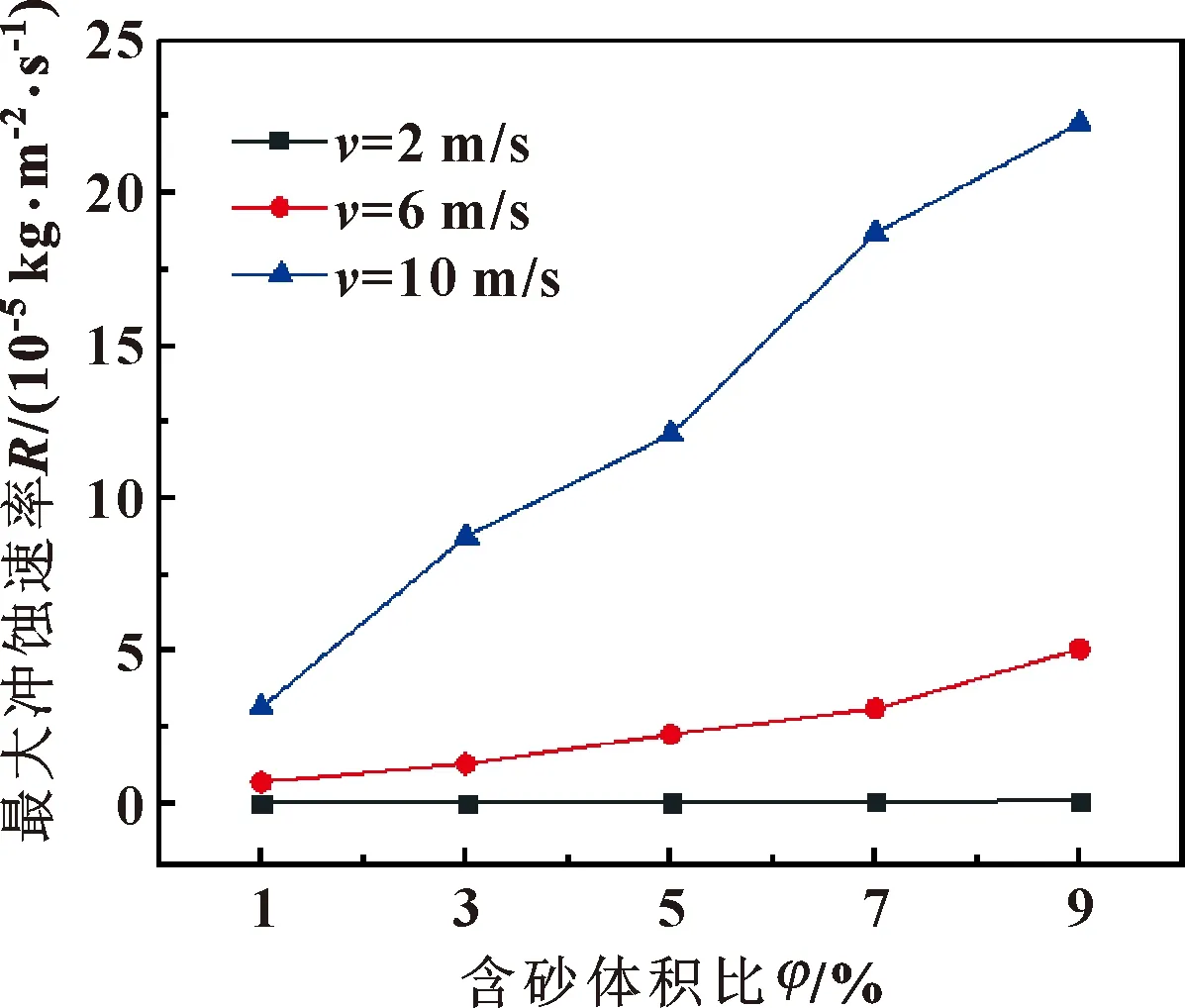
图5 不同流速下含砂体积比对冲蚀磨损的影响
图6所示为流体速度10 m/s条件下,三通管在不同含砂百分比下的冲蚀云图。可知,随着流体含砂体积比的由低到高,管道冲蚀范围增大,造成更严重的冲蚀结果。
3.3 异面管夹角对冲蚀率的影响
取砂粒直径d=0.1 mm,流体速度为6 m/s,含砂体积分数分别为1%、3%、5%条件下,分析在90°~150°异面管夹角下管道冲蚀磨损。
如图7所示,在3种不同的含砂体积比条件下,随着夹角的增加,管道冲蚀率的降低可近似视为线性减小,这主要是因为随着夹角的增大,流体的攻角变大,管道对固体颗粒的流动约束性减弱,降低了固体颗粒与管壁的碰撞概率,削弱了冲蚀作用[14]。
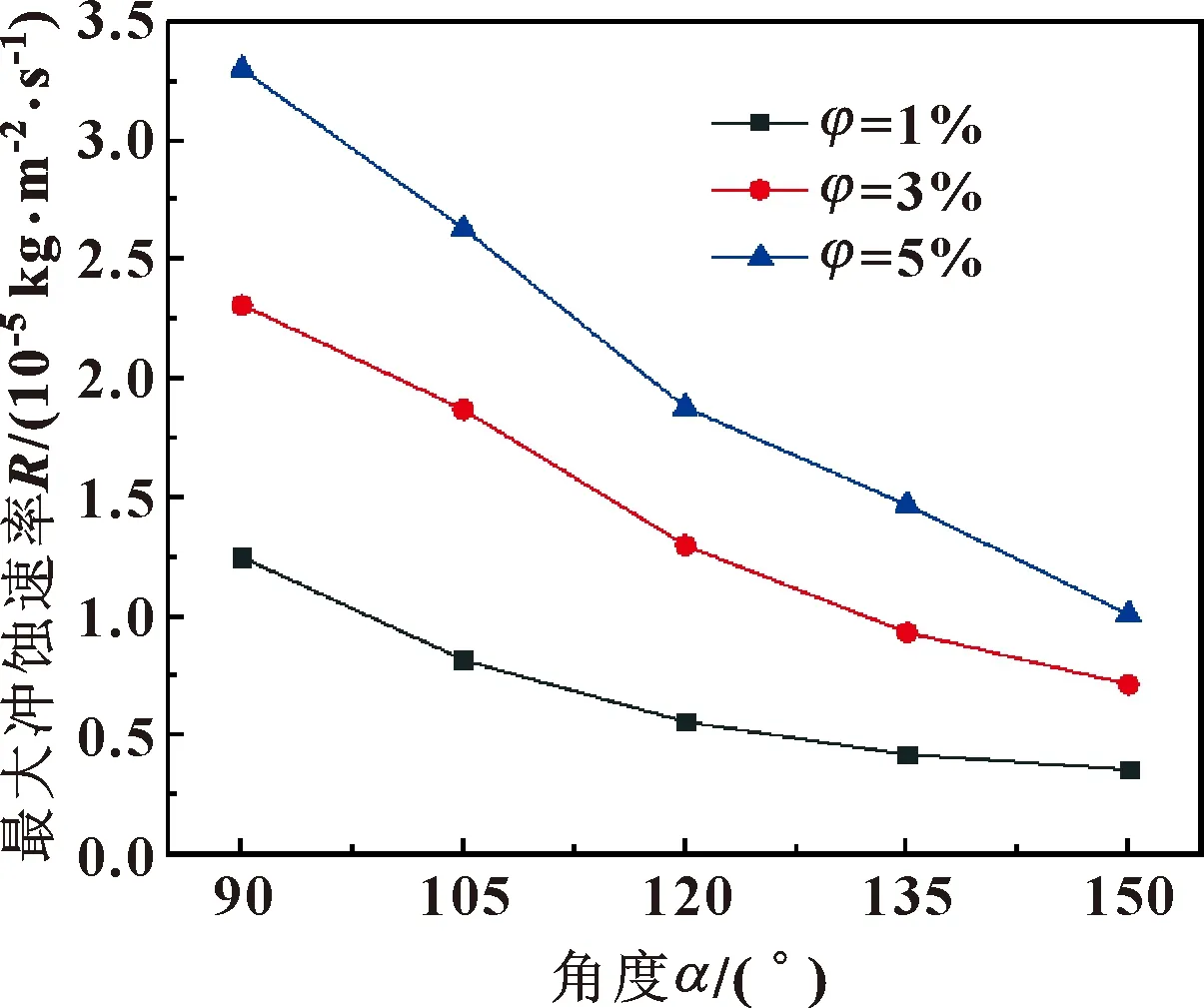
图7 不同含砂体积比下异面管夹角对冲蚀磨损的影响
图8所示为含砂体积比3%条件下,三通管在不同异面管夹角下的冲蚀云图。可知,在夹角逐渐增大的过程中,管道的冲蚀率与冲蚀区域逐步减小,这是因为:夹角的增大对流体运动的阻碍性降低,颗粒与弯头碰撞后反弹到侧壁的概率变小,因此颗粒流对壁面的冲蚀行为减弱。

图8 不同异面管夹角下冲蚀磨损云图
3.4 颗粒直径对冲蚀率的影响
建立流体速度v=6 m/s,异面管夹角α为120°,含砂体积比分别为1%、3%、5%的管道模型,探究直径为0.1~0.5 mm的固体颗粒对管道冲蚀磨损的影响。
如图9所示,在3种不同的含砂体积比条件下,颗粒直径的增大致使冲蚀率整体呈现平缓上升的趋势,这是因为:颗粒直径较小时,当颗粒随着流体的一同流动,由于自身质量较小,受到的惯性力弱,不易造成严重的冲蚀磨损;而当颗粒直径较大时,其质量的增大导致动能增强,因此对管道的冲蚀磨损更为严重[15]。
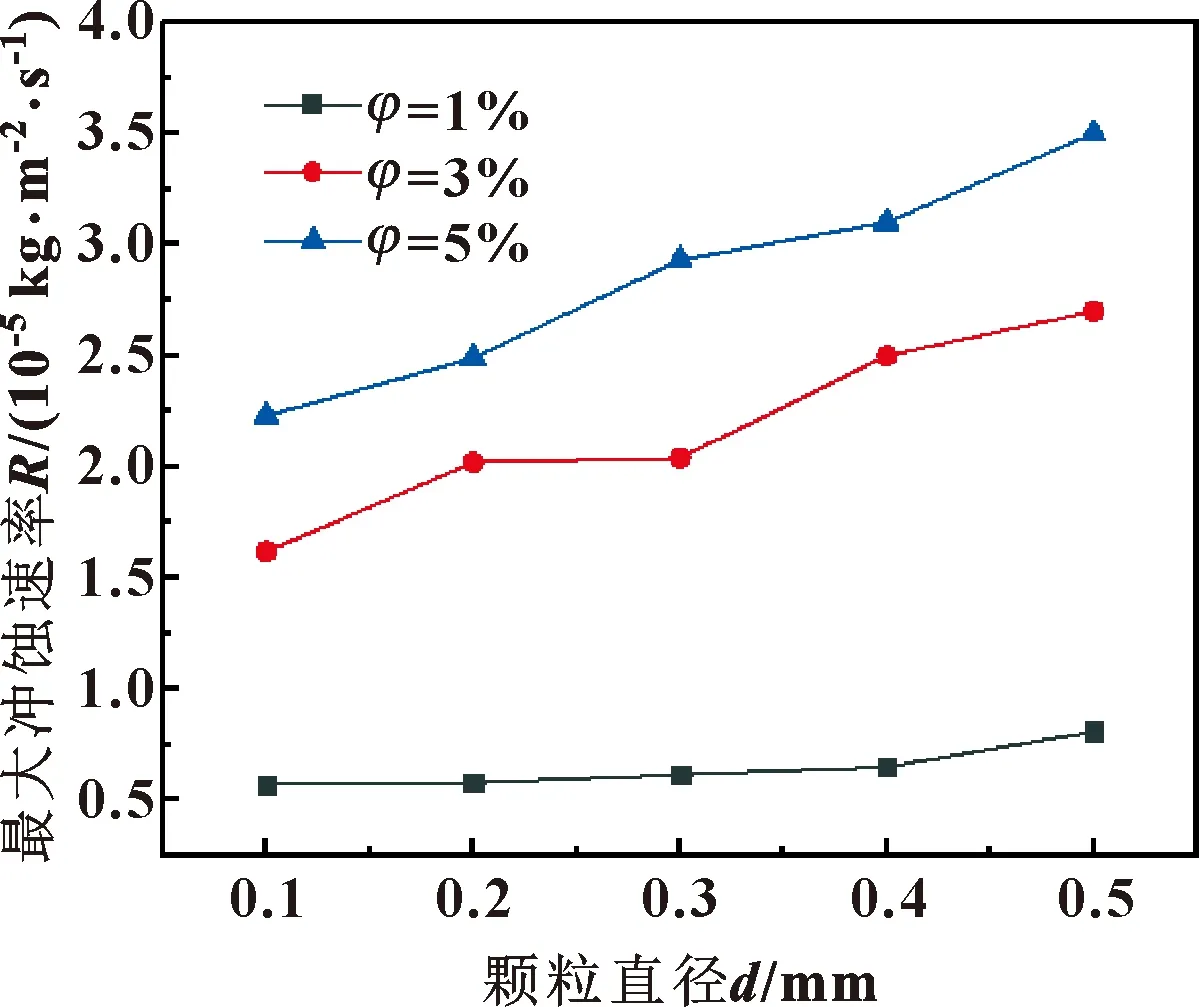
图9 不同含砂体积比下颗粒直径对冲蚀磨损的影响
图10所示为含砂体积比3%条件下,三通管在不同颗粒直径下的冲蚀云图。可知,大直径颗粒产生的冲蚀破坏相较于小直径颗粒更为集中些,管道受损程度变化较小,分析原因:流体含砂体积比不变,颗粒直径增大,单位时间内通过的颗粒数目减少,降低与壁面碰撞频率,故冲蚀率变化平稳。

图10 不同颗粒直径下冲蚀磨损云图
4 结论
(1)三管交汇处的弯面是管道主要发生冲蚀磨损的位置,最大冲蚀区域为b、c两管道弯头上侧管壁处。
(2)管道的最大冲蚀速率随着流体流速的上升而呈指数型增加,所以流速的变化对管道冲蚀磨损的影响最为显著。
(3)低流速条件下,冲蚀率随着含砂体积比的增大变化不明显;高流速条件下,冲蚀率随着含砂体积比的增大呈线性增加。
(4)在异面管夹角增大的过程中,管道对固体颗粒的流动约束性减弱,降低了固体颗粒与管壁的碰撞概率,管道冲蚀磨损率近似为线性减少。
(5)大直径颗粒产生的冲蚀破坏相比小直径颗粒更为集中,冲蚀率随颗粒直径的增大整体呈现平缓上升的趋势。

