碳纳米管/丁腈橡胶复合材料力学及摩擦性能的分子动力学模拟*

唐黎明 王新楠 纪 平 何恩球

(1.沈阳化工大学机械与动力工程学院 辽宁沈阳 110142；2.沈阳工业大学机械工程学院 辽宁沈阳 110870)

聚合物纳米复合材料因其优异的耐油性、耐磨性、黏弹性和自润滑性而被广泛应用于工业领域[1-3]。大量研究表明，聚合物纳米复合材料的力学和摩擦性能可以通过纳米增强体的固有性能和特殊结构得到增强。BOONBUMRUNG等[4]采用双辊共混法制备了MWCNTs/NBR复合材料，研究表明，以MWCNTS为增强体的复合材料相较于以炭黑(CB)、导电炭黑和沉淀二氧化硅为增强体的复合材料在拉伸强度、模量、硬度和耐磨性等方面均表现出了更大的增强量。BAI等[5]采用溶液共混法制备了氧化石墨烯/氢化羧基丁腈橡胶复合材料，由实验得出氧化石墨烯单层膜体积分数为0.44%，氢化羧基丁腈橡胶在伸长率为200%时，其拉伸强度和模量分别提高了50%和100%以上。唐黎明等[6]考察了不同类型氧化锌/丁腈橡胶复合材料的摩擦学性能，研究发现：通过改善氧化锌反应活性，缩短了胶料的硫化时间，提高了胶料的交联密度。

CNTs是一种具有卓越力学、电学、化学、光学超导特性且六边形结构连接完美的一维量子材料[7-9]。CNTs因其具有高长径比、韧性和刚度等优越性能，经常被用作纳米增强填料，来改善聚合物复合材料的性能。WU和CHEN[10]发现MWCNTs的加入显著提高了自愈脂肪酸橡胶的抗拉强度和弹性模量，而且由于刚性纳米颗粒对聚合物链的迁移率具有抑制作用，使其断裂伸长率也大大降低。SUI等[11]发现由于功能化CNTs具有增强作用，负载处理后的CNTs改性天然橡胶(NR)复合材料相较于纯NR以碳纤维(CF)/NR复合材料表现出了更优异的综合性能。JOSE等[12]考察了MWCNTs对NR基体各项性能的影响，研究发现：MWCNTs的加入很大程度上提高了复合材料的力学性能、动态力学性能、传输性能和导电性能。其中，填充量为3.5 phr的复合材料其拉伸强度相较于纯NR增加了约55%。

近年来，分子动力学已经成为在原子尺度上计算材料性质的非常有效的方法。这些模拟提供的微观信息和分子相互作用的细节，支持了广泛的实验和理论研究[13-18]。如LI等[19]运用分子模拟研究了CNTS增强聚合物复合材料的热力学性能；CHAWLA和SHARMA[20]运用分子模拟研究了CNTs增强丁苯橡胶基体的力学性能。虽然目前已经广泛开展了聚合物本征性能方面的分子模拟研究，但碳纳米材料增强丁腈橡胶(NBR)力学以及摩擦学性能模拟研究仍较为少见。为研究CNTs对NBR基体力学以及摩擦学性能的影响，本文作者建立纯NBR(以丙烯腈和丁二烯为重复单元，C3H3N和C4H6)分子模型和以CNTs为填料的NBR复合材料分子模型，从分子水平探究纯NBR基体以及CNTs/NBR复合材料的力学性能和摩擦学性能。

1 模拟方法

研究采用Materials Sudio(MS)分子模拟软件的Visualizer建模模块和Forcite计算模块完成。首先采用无规共聚物功能构建共聚体，分子链中丙烯腈与丁二烯的比例选为18∶82，与生产应用中丙烯腈质量分数为18%相对应，构造的聚合物分子链的初始构象如图1(a)所示，分子链的长度设定为10。建造(12，6)的单壁碳纳米管，扩大周期数为2，构建单壁碳纳米管周期结构，其初始构象如图1(b)所示。

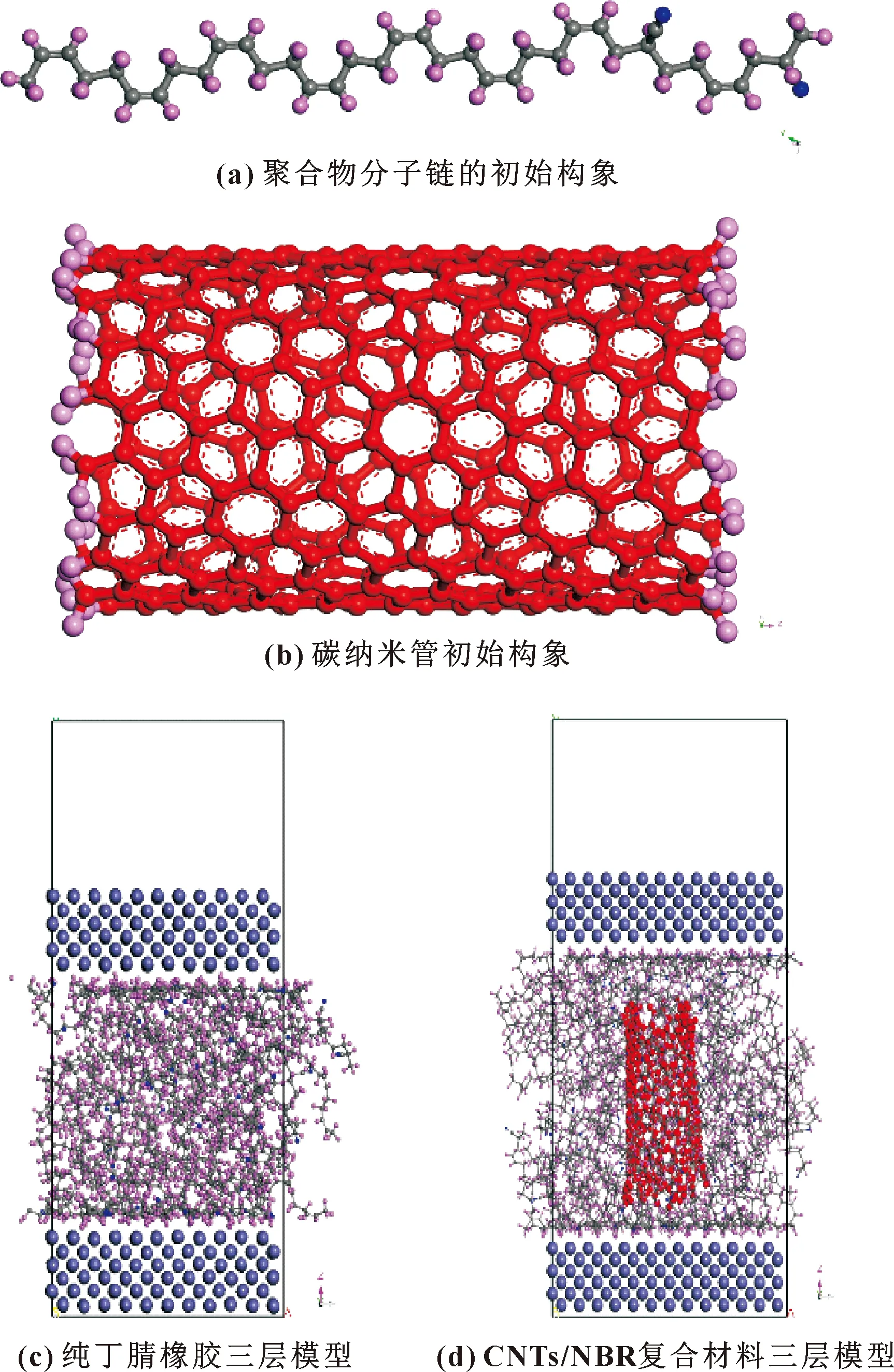
图1 材料模型

为确保后期模拟工作的精度，对碳纳米管周期性模型进行功能化处理，即对碳纳米管模型的边缘进行加氢处理[17]。研究三维周期性结构运用Amorphous Cell(AC)计算模块建立，AC模块是基于蒙特卡罗“随机数”的计算方法，因此需要建立较大的模拟单元以满足模拟计算的精确性。蒙特卡罗算法用于连接细胞中的分子，以最小化原子之间的紧密接触，同时保持原子扭转角的真实分布。选取三维模拟单元的尺寸为4 nm×4 nm×4 nm，运用AC模块的计算功能完成模拟单元的填充。

铁一般是构成摩擦配副原料的主要元素，文中选取铁元素构成3层剪切模型的上下两层形成摩擦副。铁摩擦副的尺寸为3.73 nm×3.73 nm×1.15 nm，构建的3层剪切模型如图1(c)和图1(d)所示。其中图1(c)为不含纳米填料CNTs的纯NBR材料模型，3层模型的尺寸为4.04 nm×4.04 nm×9.58 nm；图1(d)为含有纳米填料的CNTs/NBR复合材料模型，3层模型尺寸为3.73 nm×3.73 nm×8.07 nm。与纯NBR材料三维模拟单元不同，CNTs/NBR复合材料的模拟单元需要将纳米CNTs放置于单元中心以完成CNTs/NBR复合材料模型的构建。

为了获得全局和局部最小能量配置，消除不合理结构，降低内应力，需要对初始构型进行几何优化与动力学弛豫。几何优化能量收敛精度为0.48 J/mol，算法为Smart，力场为COMPASS。然后对几何优化后的模型进行动力学退火优化，退火温度范围为300～500 K，循环次数为4次，时间步长为1×10-3ps，合计模拟时长为500 ps。选取能量最低的构型进行剪切动力学模拟。

2 结果与讨论

2.1 力学性能分析

为探究CNTs对NBR摩擦学性能的增强机制，文中对比分析了纯NBR和CNTs/NBR复合材料在相同外加载荷下的力学性能。Reuss模型和Voigt模型为估算复合材料弹性模量2个最简单的模型。Reuss模型为等效弹性参数估计的下限，Voigt为等效弹性参数估计的上限，而Hill为Reuss模型和Voigt模型的算数平均值。

文中采用3种模型对比分析了纯NBR和CNTs/NBR复合材料的体积模量、剪切模量和弹性模量，如图2所示。可以看出，相比纯NBR材料，3种计算模型得到的CNTs/NBR复合材料的体积模量分别提高了16.96%、14.73%与15.83%，剪切模量分别提高了17.47%、16.05%与16.69%，沿CNTs长度方向(Z轴方向)弹性模量提高了46.05%。分析认为，在CNTs/NBR复合材料中，CNTs与NBR基体分子链结合，分子间相互作用力增大，使得CNTs/NBR复合材料具有更高的致密性以及比纯NBR基体更强的结构，所以CNTs/NBR复合材料表现出了比纯NBR材料更高的力学性能。

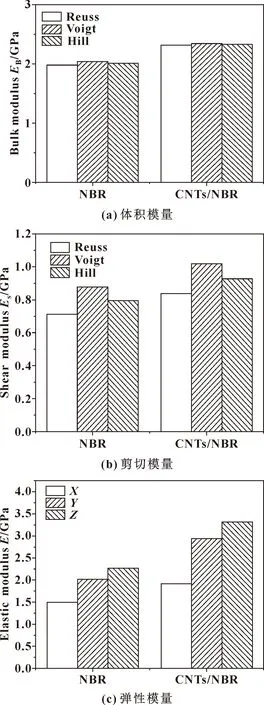
图2 纯NBR与CNTs/NBR复合材料力学性能对比

2.2 摩擦行为研究

文中首先对3层模型进行剪切模拟，对模型中的铁层沿X轴相反2个方向施加1×10-14nm/s的恒定剪切速度，时间步长为1×10-3ps，剪切模拟时间为1 000 ps，温度设置为298 K，完成剪切模拟过程。

图3分别显示了纯NBR以及CNTs/NBR复合材料在铁层剪切运动下的最终状态。如图3(a)所示，当铁层移动时，纯NBR基体经历了更大的剪切变形，但仍与铁原子粘附在一起，导致分子链出现了明显的断裂现象。如图3(b)所示，在剪切运动过程中，较少有CNTs/NBR复合材料的分子链与顶部铁层相互作用，于是CNTs/NBR复合材料比纯NBR材料磨损更少。这是由于CNTs与NBR分子链间的相互作用能，使得更多的NBR分子链被吸附和键合。因此，CNTs/NBR复合材料有更好的抵御剪切变形的能力。

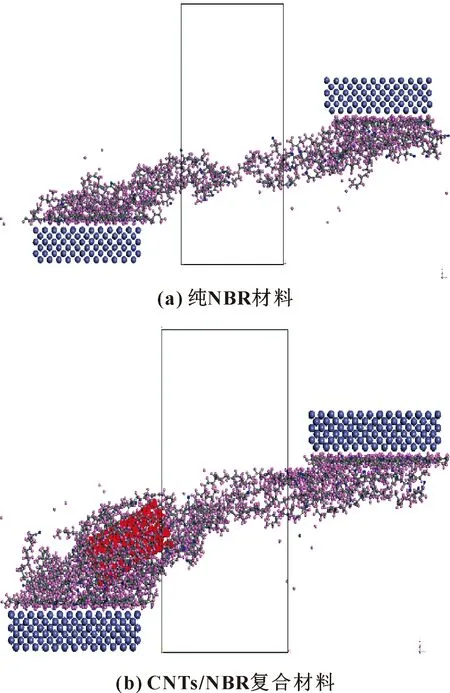
图3 材料构象

为了进一步探索CNTs的摩擦学性能增强机制，文中从浓度、径向分布函数、内聚能以及结合能等微观尺度进行分析讨论。

2.2.1 浓度

文中分析了纯NBR和CNTs/NBR复合材料摩擦模型中聚合物分子沿模型厚度(Z轴)方向的相对浓度分布，如图4所示。CNTs/NBR复合材料在接近摩擦区域的峰值浓度比纯NBR低26.12%和18.08%。

这一现象与环-块磨粒磨损试验机实验研究过程中观察到的摩擦钢环表面橡胶分子浓度的增加相符[21]。分析认为，由于摩擦过程中铁摩擦副和NBR基体间的界面吸附作用，所以纯NBR基体中更多原子会倾向于移动到橡胶基体与铁层间的摩擦区域。而对于CNTs/NBR复合材料模型而言，NBR基体中的原子更倾向于集中在NBR中心CNTs周围，这是由于CNTs表面存在很强的吸附力，使得分子间的相互作用增强，所以仅有少量的NBR分子链被铁摩擦副提供的范德华力所吸引从而产生磨损。

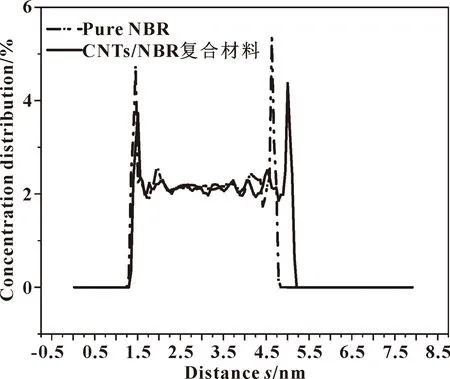
图4 纯NBR与CNTs/NBR复合材料峰值浓度分布对比

2.2.2 RDF

径向分布函数(RDF)是反映材料微观结构的一个非常重要的特征物理量，它表示在距离原子定距离的地方，找到另一个原子的概率，与完全均匀分布情况下该处找到原子的概率之比[22]。图5显示了铁原子与橡胶基体碳原子之间的RDF。在空间范围内，CNTs/NBR复合材料与纯NBR材料的RDF均值分别为0.46与0.81，纯NBR的RDF均值比复合材料上升了76.08%。因此，可以得出结论，由于分子体系中静电和范德华力的相互作用，橡胶基体分子链更趋向于吸附在CNTs周围，所以在摩擦过程中，相较于纯NBR，更少的分子倾向于向铁层移动，铁原子周围的C原子越少，铁层和CNTs/NBR之间的附着力越低。因此，添加CNTs大大降低了复合材料的摩擦因数。

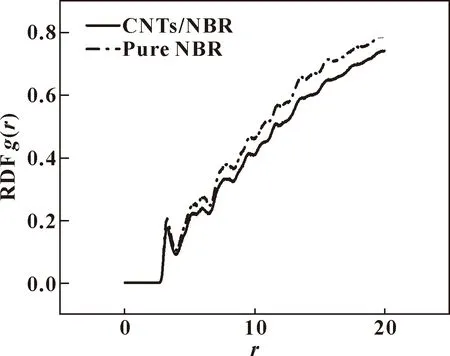
图5 纯NBR与CNTs/NBR复合材料径向分布函数对比

2.2.3 内聚能

内聚能是把所有分子分离到无限远的距离所需要的平均能量。FLEISCHER[23]在1973年提出了一个理论，指出材料在施加摩擦的过程中会产生一定的能量，同时这部分能量会以摩擦热的形式损失掉。通常，只有少部分能量可以存储在材料中。而随着摩擦过程的继续，材料中将会积累大量的能量，当能量达到一定值时，材料发生断裂失效。聚合物基体和铁层之间区域的内聚能可根据如下公式计算：

Uc=Ut-Up-UFe

式中：Ut是复合系统的总势能；Up代表聚合物的势能；UFe为铁层的势能；Uc是指界面铁层和NBR基体之间的黏着能。

在剪切过程中使用分子动力学模拟的所有数值如图6所示。CNTs/NBR复合材料的内聚能密度明显高于纯NBR。因此，CNTs的引入可以有效提高摩擦学性能。

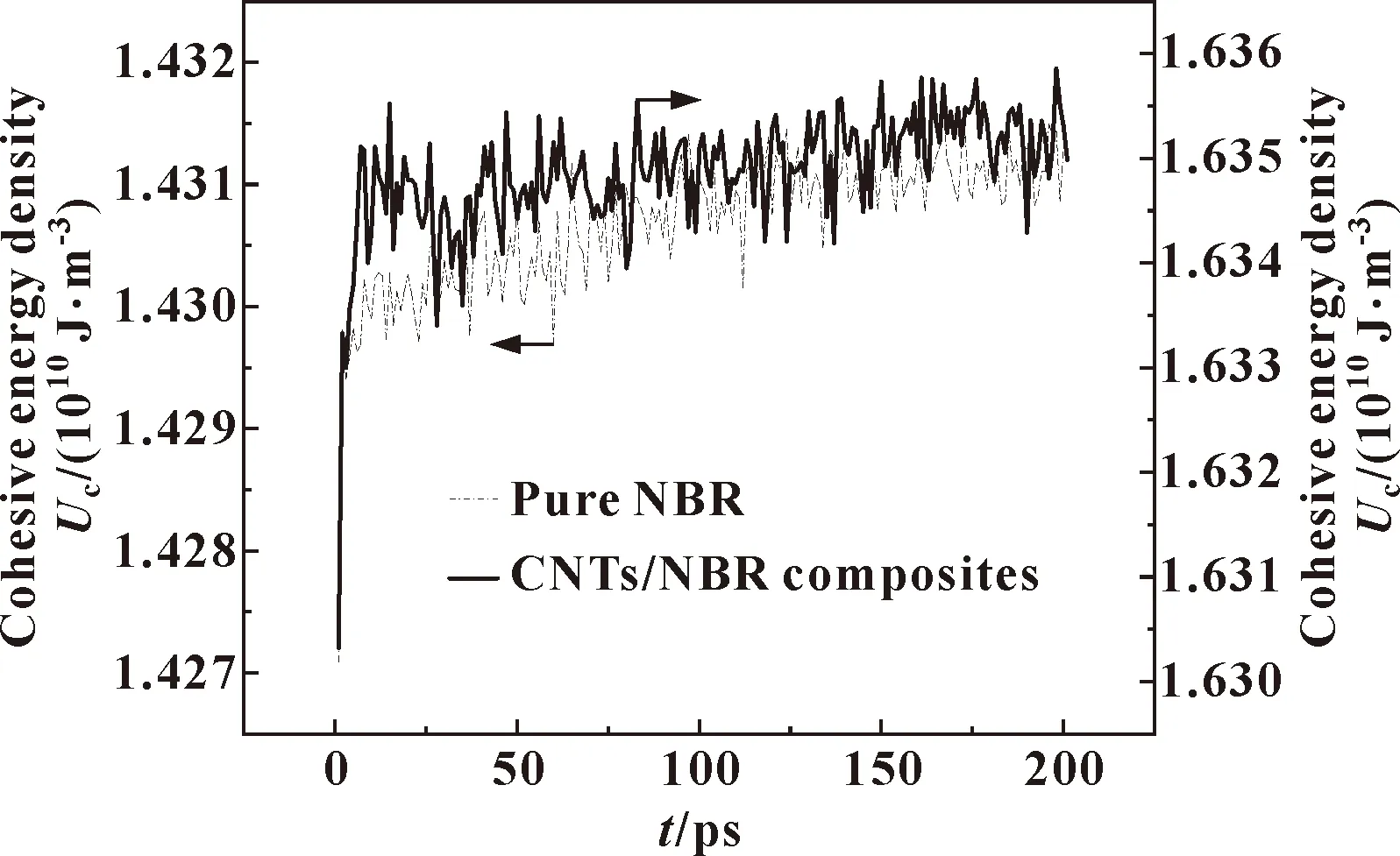
图6 在剪切过程中纯NBR和CNTs/NBR复合材料的内聚能密度

2.2.4 结合能

结合能是混合体系中不同组分相互作用能大小的量度，可定量地表征分子间相互作用力的大小。COMPASS力场被用来描述模型中原子间的相互作用，这种方法已被广泛地用于对分子和聚合物进行精确预测[24]。聚合物基体和铁层之间区域的体系结合能可根据如下公式计算：

ΔEb=-ΔEi=(EFe+Ep)-Et

式中：ΔEb为体系结合能；ΔEi是相互作用能；Et代表体系的总能量；EFe代表体系中铁组分的能量；Ep代表体系中纯聚合物或其复合材料组分的能量。

在剪切过程中使用分子动力学模拟的所有数值如表1所示。纯NBR与铁层的相互作用能较CNTs/NBR复合材料提高了约264%。

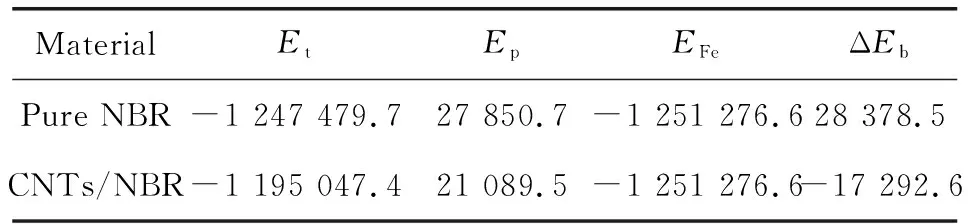
表1 剪切过程中纯NBR和CNTs/NBR复合材料体系相互作用能 单位：kJ·mol-1

3 结论

建立包含铁原子层和CNTs/NBR基体的分子层结构，通过分子动力学模拟考察CNTs/NBR复合材料的力学性能和摩擦学性能。主要结论如下：

(1)CNTs与NBR基体分子链结合，分子间相互作用力增大，使得CNTs/NBR复合材料具有更高的致密性以及更强的结构，因而力学性能也更好。

(2)CNTs/NBR复合材料在接近摩擦区域的峰值浓度比纯NBR低26.12%和18.08%，在空间范围内，纯NBR的RDF均值比复合材料上升了76.08%，纯NBR相互作用能较CNTs/NBR复合材料提高了约264%，CNTs/NBR复合材料的内聚能密度也明显高于纯NBR。因此，在摩擦过程中，CNTs与NBR分子链结合增多，分子间相互作用力增大，两者之间逐渐形成了三维网络从而提高了复合材料的力学性能和摩擦学性能。