直驱控制涡旋压缩机位置识别方法研究*

颜禧龙,蔡炯炯*,蒋加祯,瞿 晓,刘 雷

(1.浙江科技学院 自动化与电气工程学院,浙江 杭州 310023;2.思科涡旋(杭州)有限公司,浙江 杭州 310023)

0 引 言

涡旋压缩机是20世纪80年代才发展起来的一种新型容积式压缩机。该型压缩机具有零件少、体积小、运转平稳、振动小、效率高等优点,因而被广泛应用于众多的工业制造领域中[1-3]。随着工业技术的进步与发展,业界对于涡旋压缩机的要求也越来越高。

在涡旋压缩机的工作过程中,由于气体会从其动、静涡盘齿壁间的径向间隙泄露,这大大阻碍了涡旋压缩机往高压力、大容量方向的发展[4]。因此,密封问题一直是涡旋压缩机研究的关键技术难题之一。

涡旋压缩机动、静涡旋齿壁间的径向间隙是其气体泄漏的主要通道之一。径向间隙又包含静态间隙和涡旋压缩机工作过程中和动态间隙。其中,静态间隙主要是由动静涡旋盘的加工误差、各运动部件的磨损、装配精度不够等引起的;动态间隙主要是涡旋压缩机工作状态下,因中间传动环节的传动误差和防自转机构不能完全控制动涡盘的自转,而由此引起的[5,6]。

近年来,国内外许多学者和专家就涡旋压缩机的切向泄露和密封相关问题进行了大量研究工作。

PEREIRA E等人[7]对不同气体、工况和几何参数下,涡旋压缩机的切向泄漏问题进行了数值分析。KOHSOKABE H等人[8]对涡旋压缩机进行了研究,结果发现,利用代数螺线作为涡旋型线有利于减小压缩机切向泄漏线的长度。刘兴旺等人[9]也对涡旋压缩机进行了研究,结果发现,单位曲柄转角下的切向泄露量会随着转速降低而增大。王海民等人[10]通过对涡旋压缩机进行的研究,并指出,压缩机径向间隙处的密封是靠油膜表面张力来完成。ZHENG S Y等人[11]对涡旋压缩机进行了研究,在此基础上指出,通过在静涡盘侧壁上设置连续密封槽,可以减少切向泄露量。KYOBONG K等人[12]考虑了涡旋压缩机轴和套筒之间的接触和油膜压力的影响,对径向随变机构进行了动力学研究。

上述研究工作虽然对涡旋压缩机切向动态密封的改善提供了很多有益的帮助,但是由于大部分的机构比较复杂,且大部分不适用于无油压缩,其对切向动态密封的改善效果有限。另外,在上述研究工作中,对动、静涡旋齿间的径向间隙均无法实现主动控制,结果是在2个涡旋盘之间仍然存在切向泄露和过摩擦现象,给涡旋盘的稳定转动带来了新考验。

为解决上述研究中存在的问题,笔者提出一种基于电流信号的涡旋压缩机切向主动密封的控制方法,并在平面电机上,利用该控制方法实现对动、静涡旋齿间径向间隙的主动控制。

1 涡旋压缩机直驱主动控制特性

1.1 基于直线电机的直驱式涡旋压缩机构架

针对涡旋压缩机侧面动态密封问题,笔者提出一种基于平面电机的直驱式涡旋压缩机构架。平面电机由2个永磁同步直线电机(在运动方向上成90°角)构成XY电机平台[13],电机带动动涡盘沿规划好的运动路径进行平面运动,即可实现对涡旋压缩机动静涡盘间径向间隙的主动控制。

基于直线电机的直驱构架示意图如图1所示。

图1 基于直线电机的直驱式涡旋压缩机构架示意图

相比于传统的驱动方案,该直驱方案减少了电机与动涡盘之间的传动环节和防自转机构,使其结构更为简单;而且也减少了因中间传动结构带来的传动误差,能更精准地控制涡旋压缩机动静涡旋齿间径向间隙的大小,从而提高其动态侧面密封效果。

1.2 侧面密封接触压力与电流信号特征

在涡旋压缩机的工作过程中,其内部动静涡旋盘的啮合情况(即径向间隙的大小)不能直接得到,因此,笔者在该处采用电机电流变化来间接判断动静涡旋盘的啮合情况。

在理想的情况下,设通入绕组的三相电流为:

(1)

式中：Im—电流幅值；ω—电流角频率；θ0—A相电流初始相位角。

设A相线圈初始位置为X0，到t时刻空间位移为xt，则A相线圈反电势为[14-16]：

(2)

式中：n—线圈匝数；Bm—磁场强度；l—叠厚；τ—极距。

动子速度为：

(3)

(4)

此外，对永磁同步电机有:

(5)

即永磁同步直线电机的推力公式可表示为:

(6)

但实际上直驱电机平台除了对负载输出力之外，还要平衡摩擦力、本身的开断引起的端部力等，其机械运动方程可表示为:

F=MpV+Ff+Fr+Fd

(7)

式中：F—电磁推力；M—动子质量；p—微分算子；Ff—摩擦力；Fr—由于端部效应、齿槽效应和其他因素引起的波动力，其占比随着负载程度略有变化；Fd—负载力。

由于电磁推力存在波动和三相反电势非正弦，所以三相电流也非正弦，对每个位置仍采用通入三相对称电流的控制方案，则式(6)变为:

(8)

则三相电流表达式为:

(9)

由式(4,8,9)可知：在速度V不变的情况下，三相反电势(Ea、Eb、Ec)在每个确定的位置(θ)处为不变恒定量，因此，电流幅值(I)和电磁推力(F)成比例关系。所以笔者可以通过三相电流(ia、ib、ic)的大小来获知电磁推力(F)的大小。并且电磁推力会随着侧面密封接触压力的变化而变化，所以可以通过电机某相电流的大小来反映出侧面密封接触压力的变化。

1.3 直驱式切向主动密封控制方法

基于上文对涡旋压缩机侧面密封接触压力与电机电流信号的分析可知,当电机电流增大时,其侧面密封接触压力也随之增大。

因此,笔者提出一种基于电流信号的涡旋压缩机切向主动密封的控制方法。

基于电流信号的直驱控制方法流程图如图2所示。

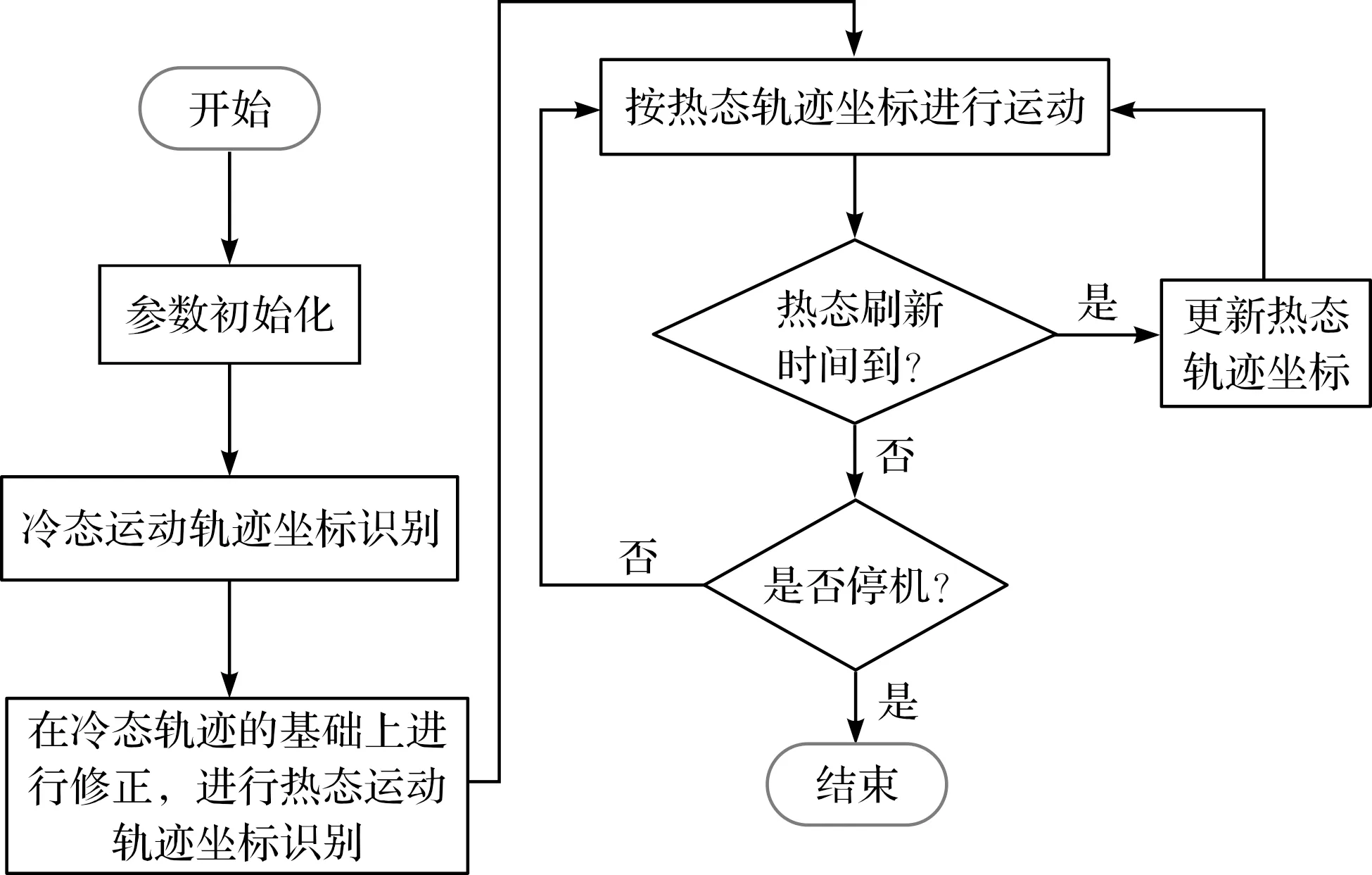
图2 基于电流信号的直驱控制方法流程图

该控制方法的流程是先进行冷态位置识别,再进行热态位置识别。因为与热态时相比,冷态时涡旋压缩机的零部件形变小,受温度影响小,所以对其进行控制的难度更小。并且冷态位置识别可以为热态位置识别奠定基础。[17]

2 冷态运动轨迹识别

冷态位置识别过程主要分为4部分:

(1)建立离线电流数据库;(2)确定电流差值阈值;(3)确定静涡盘圆心;(4)确定动涡盘运动轨迹。

冷态运动轨迹识别算法流程图,如图3所示。

冷态运动轨迹详细识别步骤如下:

(1)建立离线电流数据库(如图3框1部分所示)。基于前期对电机电流信号的分析可知,当负载和速度一定时,电机相电流值在每个固定位置是确定的,因此,笔者提出构建离线电流数据库;

(2)确定电流差值阈值(如图3框2部分所示)。通过将当前电流值与数据库中相同位置的电流值进行比较，得到电流差值Δi1，再以电流差值Δi1为评价指标，以此来判断动静涡盘的啮合情况，电流差值Δi1=|当前电流i-数据库电流i0|；

图3 冷态运动轨迹识别算法流程图

为了确定电流差值的阈值，笔者先控制电机往X轴正方向运动，直到二维力传感器数值达到一定值时停止，记录此时的电流值，选取合适的电流差值使力传感器数值最小。其他3个方向也是如此，最后选取最大值确定为电流差值阈值I1；

(3)确定静涡盘圆心(如图3框3部分所示)。当安装好动静涡盘时,其圆心位置可由光栅反馈得到,而静涡盘圆心位置无法得知,因此就无法进行动涡盘运动轨迹识别。确定静涡盘圆心分为两步,即先初步确定圆心坐标,再在此基础上,多次测量求平均,确定最终的圆心坐标。

确定静涡盘圆心示意图如图4所示。

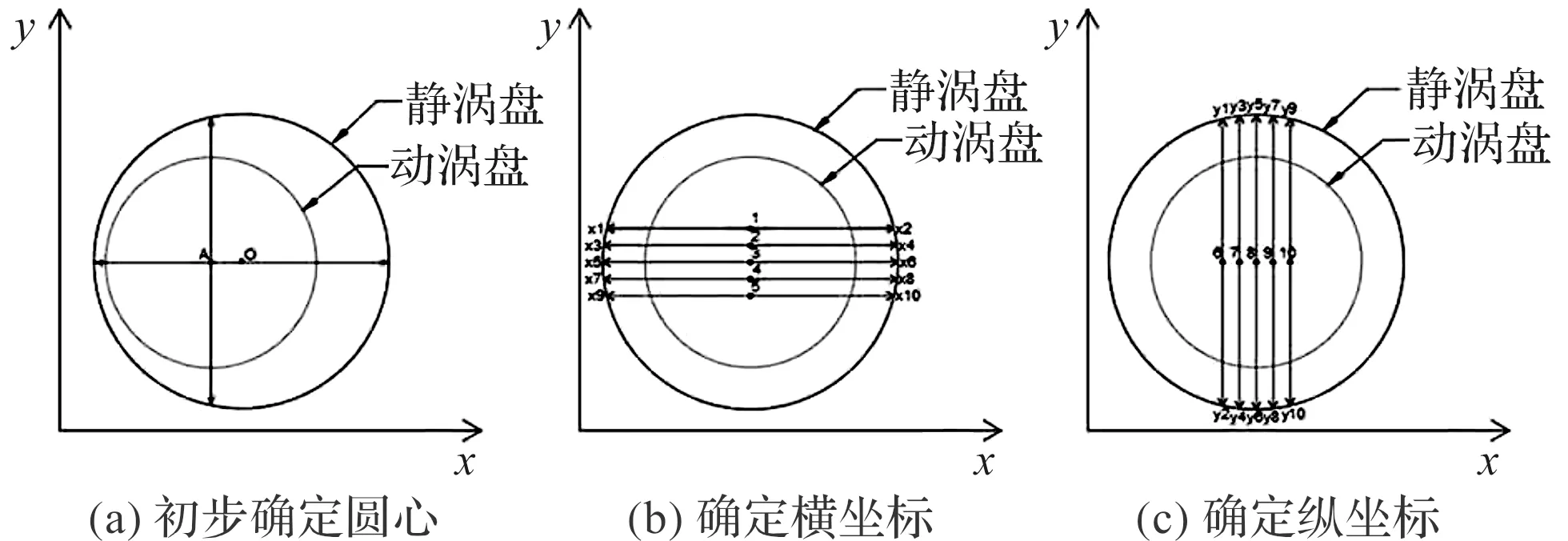
图4 确定静涡盘圆心示意图

图4(a)为初步确定静涡盘圆心坐标，在确定X轴中心坐标时，电机的Y轴不动，只移动X轴，控制电机先向X轴正方向移动，当检测到电流差值大于阈值时，记录该点坐标为电机X轴正边界坐标。同理，可以得到电机X轴负边界坐标，然后将两坐标求中间值，就得到了X轴中心坐标(Y轴中心坐标也是如此测得)。

为了减小误差，笔者以初步测得的圆心为测量起点，X轴和Y轴各重复测量5次，如图4(b，c)所示，将所得结果求平均确定为静涡盘圆心；

(4)确定动涡盘运动轨迹(如图3框4部分所示)。由于存在加工误差和装配误差,需要对压缩机动涡盘运动轨迹进行识别确定。

冷态位置识别示意图如图5所示。

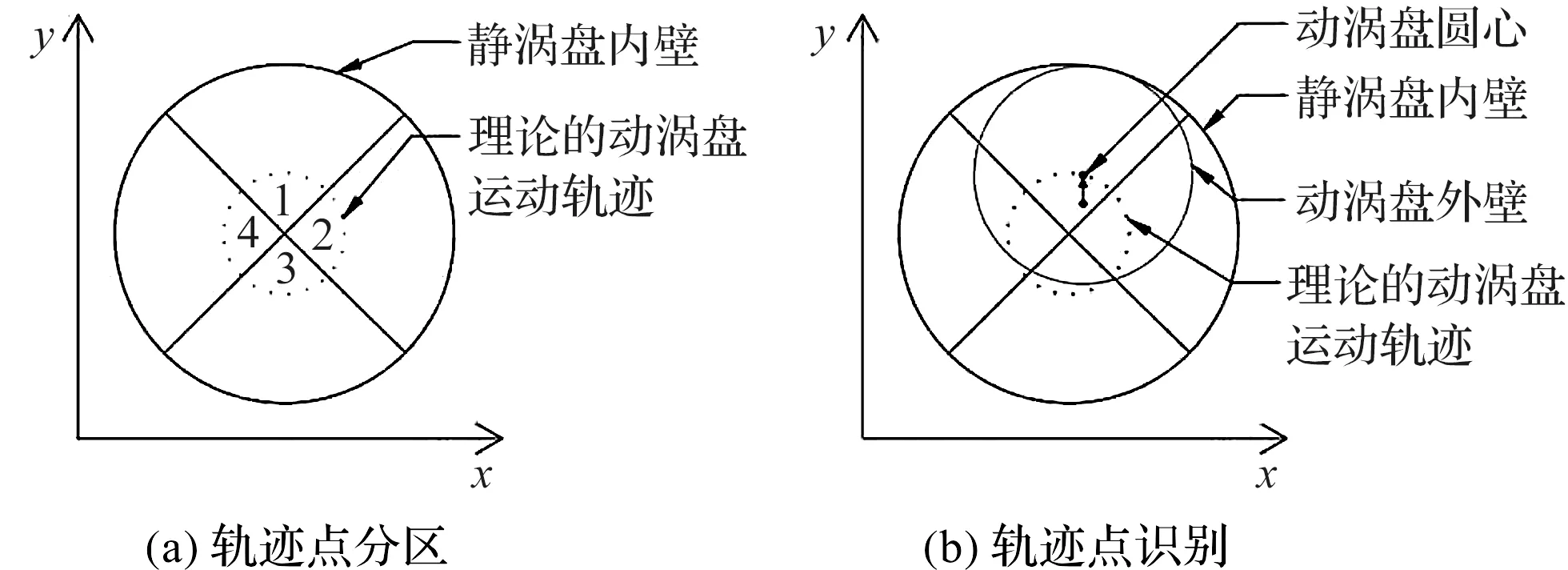
图5 冷态位置识别示意图

笔者将理论的压缩机动涡盘运动轨迹均匀分为等份,算出待测n个点的坐标,如图5(a)所示,按角度将动涡盘运动轨迹平均分为4个部分。如图5(b)所示,测量第一部分的点，电机X轴不动,移动电机往Y轴正方向运动,每前进一步测量一次电机电流,当检测到电流差值大于阈值时，记录并保存该点坐标;

其他3部分也是类似的操作,直至测量完所有点的位置,最后将所有测得的点坐标组合而成为动涡盘运动轨迹坐标。

3 热态运动轨迹识别

在涡旋压缩机运行时,由于气体压缩发热,会导致压缩机的动、静涡盘受热变形,仍沿冷态轨迹运动会出现过摩擦或切向泄露,因此,需要修正其运动轨迹。

热态位置识别主要分为确定热态运动初始轨迹、确定电流差值阈值和修正动涡盘运动轨迹3部分。

热态轨迹识别流程图如图6所示。

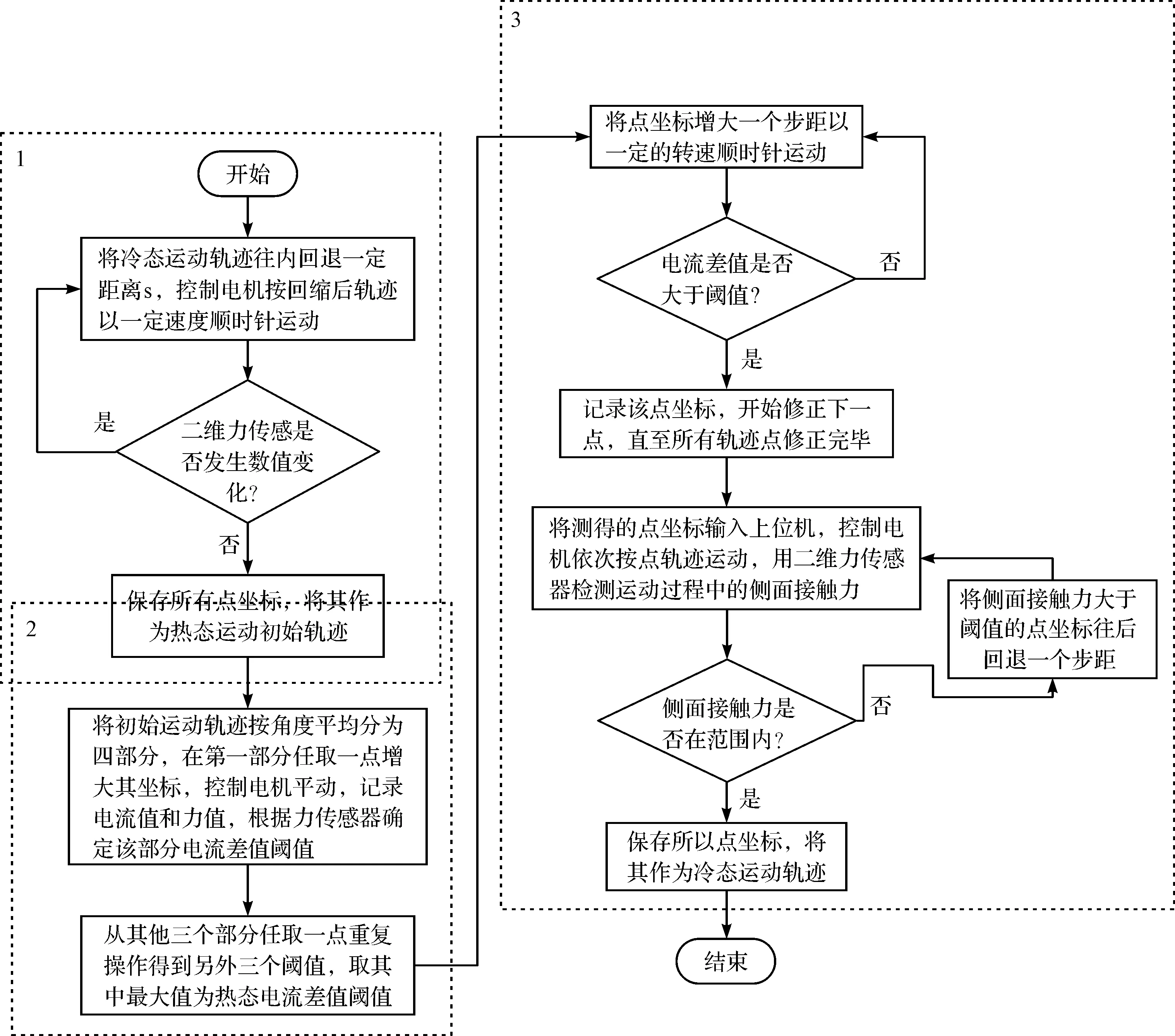
图6 热态轨迹识别流程图

热态轨迹识别步骤如下:

(1)热态初始运动轨迹的确定(如图6框1部分所示)。热态运动初始轨迹是在已有的冷态运动轨迹基础上的适度缩减,其目的是为了防止涡旋压缩机在运行过程中发生热膨胀等磨损现象。

为了确保压缩机动涡盘沿热态初始轨迹运行时不会和静涡盘发生接触,需用二维力传感器来进行检测。

笔者将冷态运动轨迹往内回缩一定距离,控制电机按回缩后轨迹以一定速度顺时针运动,若力传感器有数值变化则需要再缩减一定距离,直至力传感器无变化,即认为动、静涡盘无接触,保存运动轨迹为热态运动初始轨迹。

笔者确定其热态初始轨迹示意图如图7所示;

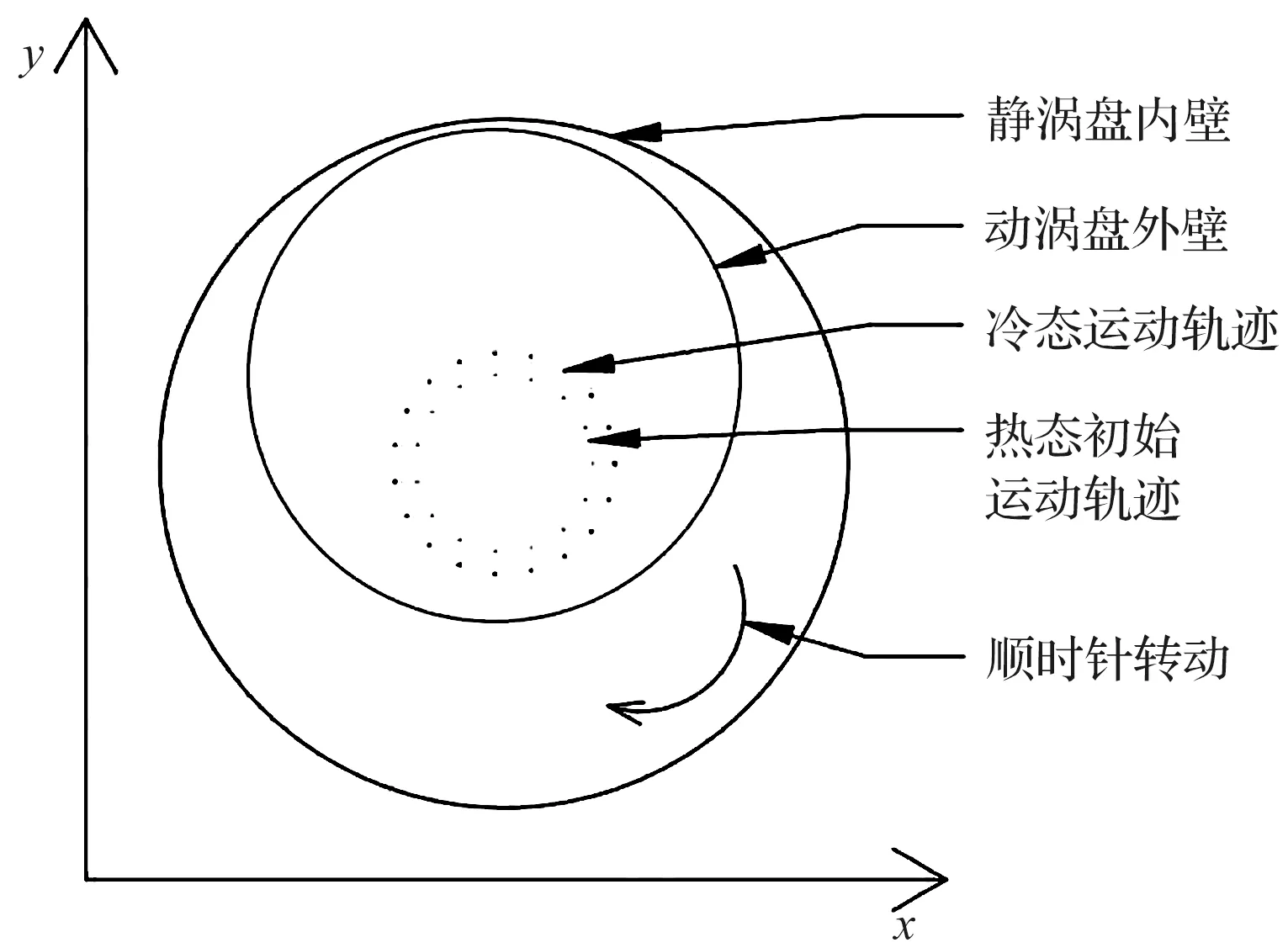
图7 确定热态初始轨迹示意图

(2)电流差值阈值的确定(如图6框2部分所示)。与冷态运动不同,热态运动轨迹识别的评价指标是以当前位置电流值和上一位置电流值的进行比较,得到的电流差值Δi2作为评价指标。其中,电流差值Δi2=|当前位置电流ip-上一位置电流iq|。

笔者从初始轨迹上选取4个端点,先将X轴正向端点横坐标每次增加一定距离,其余点不变,控制电机按更改后轨迹,以一定速度顺时针运动;根据待测点电流值和二维力传感器数值确定动静涡盘在待测点处刚接触和未接触时的电流差值阈值;再将其他3点进行上述操作,得到另外3个电流差值阈值,并取其中最大值作为热态电流差值阈值I2;

(3)动涡盘运动轨迹的修正(如图6框3部分所示)。

热态位置识别示意图如图8所示。

图8 热态位置识别示意图

图8(a)中,将热态初始轨迹按角度平均分为4部分,先选取第一部分中一点,逐渐增加其纵坐标,其余点坐标不变,控制电机按更改后轨迹,以一定速度顺时针运动,得到图8(b)所示结果。

当待测点电流差值大于阈值I2，即认为动静涡盘在该点发生接触,将其回退一最小步距作为热态轨迹上的点。以此往复,直至修正完所有轨迹点,从而得到热态运动的轨迹坐标。

4 实验及结果分析

为了对笔者提出的基于电流信号的涡旋压缩机切向主动密封的控制方法进行有效性验证,笔者搭建了相应的实验平台。

因为涡旋压缩机工作时,其动涡盘绕静涡盘圆心作半径为r的圆周运动,所以笔者在此处将动静涡盘简化为2个半径大小不同的圆环。

笔者所采用的实验平台示意图,如图9所示。

图9 实验平台示意图

在此实验平台中,各设备的具体型号参数如表1所示。

表1 实验设备型号参数

4.1 冷态轨迹识别实验

冷态轨迹识别实验的相关参数如下:

静涡盘内直径为56 mm,动涡盘外直径为50 mm,动涡盘运动半径为3 mm,动涡盘运动步距为100脉冲数即10 μm。

经过反复多次实验,笔者得到电流差值阈值I1为0.04 A,电流差值与接触力关系图如图10所示。

图10 电流差值与接触力关系图

取n=60,即可得到冷态轨迹的识别结果图,如图11所示。

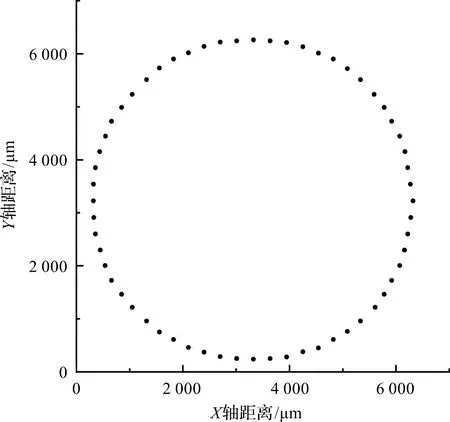
图11 冷态轨迹识别结果图

为了验证冷态位置识别效果,笔者将采集到的点坐标输入上位机,控制电机按顺序移动到每个测量点位置,并采用二维力传感器,检测运动过程中动静涡盘之间侧面接触压力。

冷态侧面接触压力与角度的关系图如图12所示。

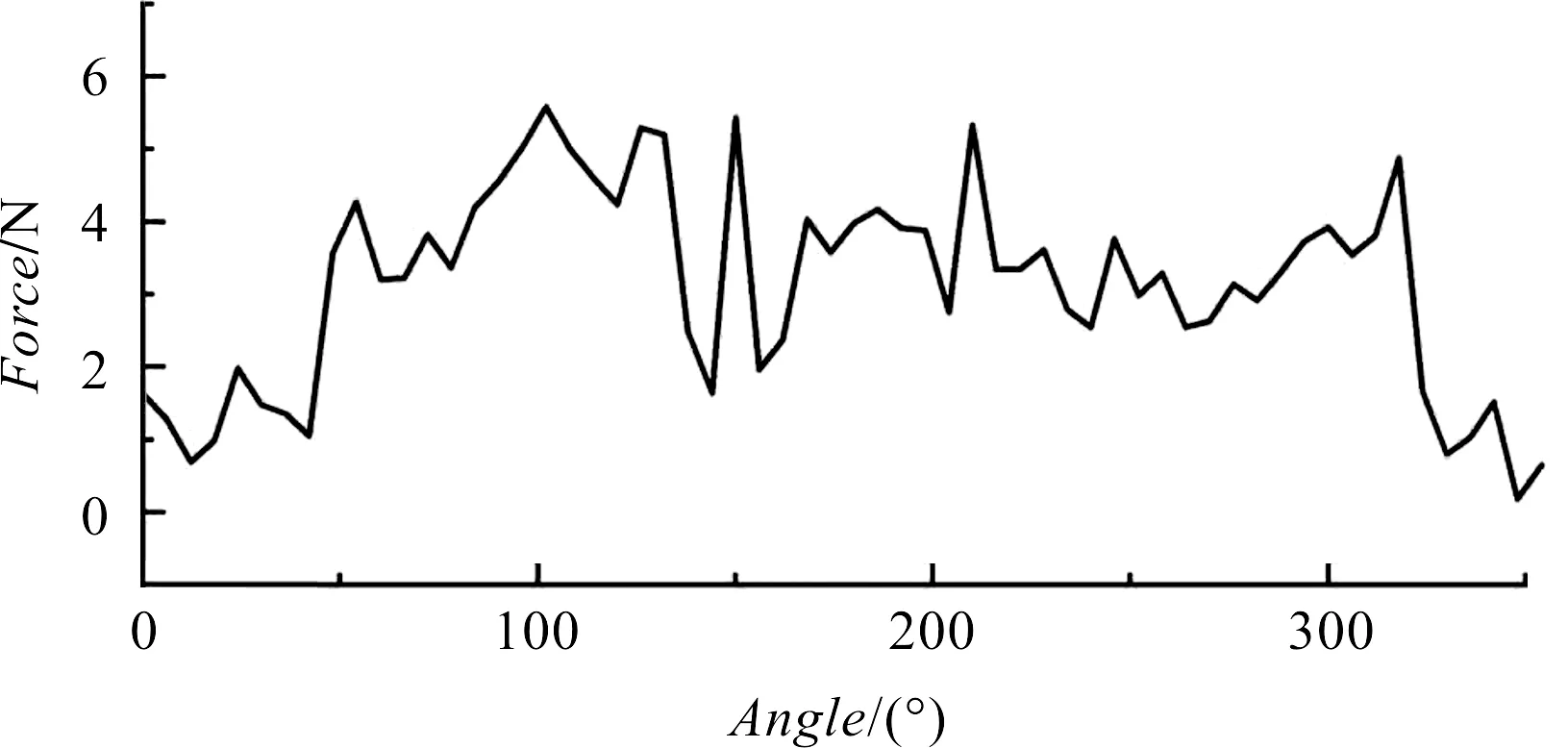
图12 冷态侧面接触压力与角度的关系图

由图12可知,动静涡盘间侧面接触压力小于6 N。

4.2 动态轨迹识别实验

做热态实验时,需要涡旋压缩机进行气体压缩。由于热态实验成本高,且其装备复杂,为了方便实验,此处笔者采用与冷态实验相同的元器件进行动态轨迹识别实验。

笔者设定电机的运动频率为1 Hz,经过反复实验得出电流差值阈值I2为0.1 A,并取n=60,得到的动态轨迹识别结果图如图13所示。

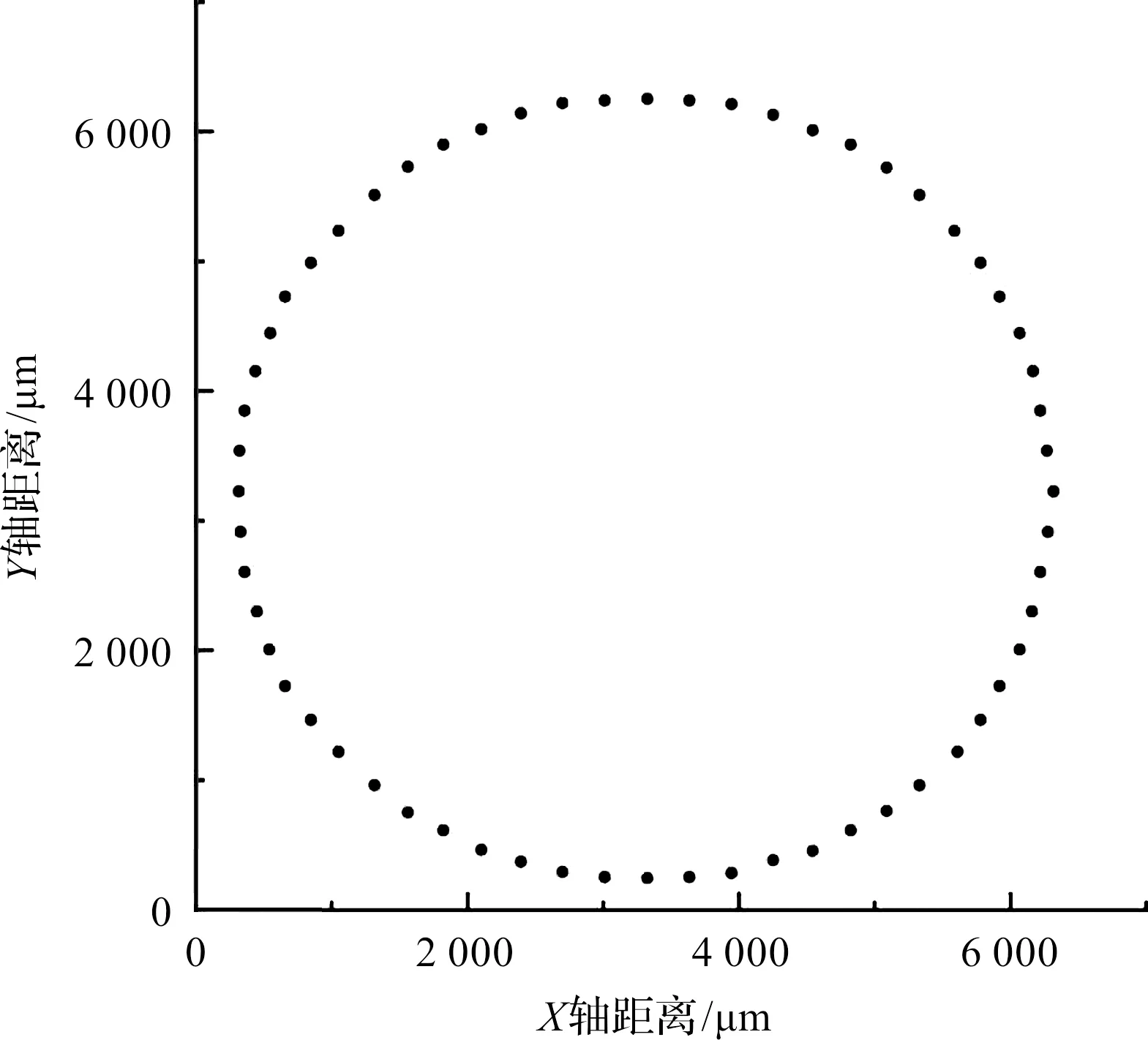
图13 动态轨迹识别结果图

为了验证动态位置识别效果,笔者将轨迹点坐标输入上位机,控制电机以1 Hz频率运动,并采用二维力传感器,检测运动过程中动、静涡盘之间侧面密封接触压力。

动态侧面密封压力与角度的关系图如图14所示。

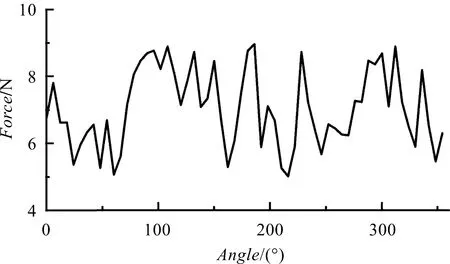
图14 动态侧面密封压力与角度的关系图

由图14可知:动、静涡盘间侧面密封接触压力在10 N以内,通过牺牲少量磨损即可增加侧面密封效果。

5 结束语

目前,涡旋压缩机切向密封方案复杂、灵活性差、成本高,针对这些问题,在分析了涡旋压缩机动态径向间隙特点的基础上,笔者提出了一种基于电流信号的涡旋压缩机切向主动密封的控制方法。最后,为了对基于电流信号的涡旋压缩机切向主动密封的控制方法进行有效性验证,搭建了相应的实验平台。

研究结论如下:

(1)涡旋压缩机动静涡盘的侧面密封接触力越大,说明啮合越紧;接触力可以通过电流差值大小反馈得知,其随着电流差值的增大而增大;

(2)在压缩机冷态和动态运动时,采用基于电流信号的涡旋压缩机切向主动密封控制方法,都能够较好地识别动涡盘运动轨迹位置,提高涡旋压缩机的切向密封效果。

上述研究为涡旋压缩机提供了一种直驱式、主动控制的侧面动态接触密封方法,具有结构简洁、宽调速范围等优点。但是受限于实验成本等因素,热态实验采用了与冷态实验相同的元器件。

因此,在后续的工作中,笔者将在上述研究的基础上,进行涡旋压缩机全负载热态研究和其速度极限特性的研究。