基于敏感特征频带的旋转机械故障源定位方法*

谭 逸,马 波,2,张强升

(1.北京化工大学 机电工程学院,北京 100029;2.北京化工大学 高端机械装备健康监控与自愈化北京市重点实验室,北京 100029;3.生态环境部 核与辐射安全中心,北京 100082)

0 引 言

当前,旋转机械被广泛应用于核电、石化和航空航天等领域[1]。

旋转机械在发生故障时,由于振动过大激励出明显的声音,其中含有大量的故障信息[2]。通常,在旋转机械表面布置多个振动传感器,监测设备的运行状态。但是该方法不适用于对高温、高压以及高腐蚀的环境下运行的设备进行状态监测[3]。

声信号监测通常采用非接触式测量方式,即通过声阵采集旋转机械的声音信号,利用声源定位方法识别故障源的空间位置。该方法具有较高的监测效率和良好的工程应用价值。由于声阵信号来源广泛,且其中包含故障声信号和其他干扰信号,从中确定含有故障信息的频率范围,对于准确识别故障源的位置具有重大意义。

目前,许多学者基于声阵技术开展了机械设备的声源定位方法研究。常用的声源定位方法主要包括如下3种:时延估计方法[4]、高分辨率谱估计方法[5]和波束形成方法[6],具体分述如下:

(1)时延估计方法。针对时延估计方法中时延计算不准确的问题,刘志强等人[7]通过提高采样率降低时延值的误差,对锅炉炉管的泄漏位置进行了定位。ZHANG X等人[8]构建了Teager能量谱峰度指标,以此来选取含有故障信息的子带,实现了对带式输送机的故障源定位;但对于多故障情况下定位,该方法存在精度不足的问题。时延估计方法仅适用于单声源定位,其鲁棒性较低,且极易受噪声干扰,导致其时延提取不准确,造成定位方程组无解或定位偏差较大;

(2)高分辨率谱估计方法。采用高分辨率谱估计方法对非平稳信号进行定位分析时,需预先知道声源的数目。薛先岭等人[9]通过频域数据模型的短时功率谱联合对角化特性,对声源位置进行了估计;但该方法对于低信噪比环境存在使用上的局限性。张楠等人[10]将多重信号分类方法应用于机车驱动系统的故障轴承定位,并分析了阵列结构参数对定位精度的影响。高分辨率谱估计方法计算量较大,在声源数目不确定,且识别效率要求高的应用场景不适用;

(3)波束形成方法。波束形成方法具有计算速度快、定位精度高和识别声源多的优点。谭龙龙等人[11]34-35通过频谱分析确定了声源信号的中心频率,利用常规波束形成方法识别了离心压缩机的声源位置;但该方法对旁瓣抑制能力不足,声源分辨率较低。张自嘉等人[12]对多种波束形成方法开展了仿真实验研究,分析得到了自适应波束形成方法;该方法较常规波束形成具有更好的旁瓣抑制效果,但缺乏实际的实验验证。翟春平等人[13]将最小均方无失真响应(minimum variance distortion response, MVDR)方法应用于舰船的噪声源识别领域,人为选取了不同频段的信号,并进行了定位实验分析,实验结果表明：低频段噪声源的定位精度明显低于高频段噪声源,证明了自适应波束形成方法更适用于高频段声源定位;但该方法在水下复杂声场环境下,对于振动耦合的噪声源识别精度较低。

基于波束形成原理开展的声源定位研究虽然已取得了一定的成果,但仅通过专家经验人为选择一定频率范围的声阵信号,存在漏失目标声源信号的可能性,导致其定位不准确。

在信号传递过程中,旋转机械故障信号往往会被自身固有频率调制至高频段,该频带信号具有明显的周期性冲击特性。波束形成方法具有高频段定位精度高的特点,选取调制后的敏感特征频带进行定位计算,可以获得较好的定位效果。

由于不同故障频带信号之间存在明显的差异性,对于旋转机械故障源定位所需的频带范围难以固定,因此,针对不同的故障类型选取含有故障信息的敏感特征频带进行定位分析尤为重要。

Protrugram方法最早由BARSZCZ T等人[14]提出,用于识别信号中具有最大冲击特性的频带,在故障诊断领域得到了广泛应用。代荡荡等人[15]提出了一种Protrugram与小波变换结合的方法,成功确定了局部放电的冲击脉冲信号所在频带,再利用小波降噪实现了对多类噪声的有效抑制。WANG Z等人[16]提出了通过Protrugram方法提取谱峰度熵,并结合机器学习方法,实现了对机车转向架故障的诊断。DU J等人[17]利用Protugram方法,提取了反映轴承内外圈故障特征的敏感特征频带,并结合Lempel-Ziv指标,实现了对轴承故障的定量趋势诊断。

上述研究表明:Protrugram方法对于信号中的冲击成分敏感程度高,可以精准地识别具有冲击特性的频带。

综上所述,基于旋转机械的故障特性,笔者利用Protrugram方法选择敏感特征频带,采用MVDR方法,对位于高频段的敏感频带信号进行定位分析;同时设计故障模拟实验,以验证该方法的有效性。

1 理论基础

1.1 Protrugram方法

Protrugram方法是一种固定带宽迭代搜索最大峭度频带中心频率的计算方法。该方法的基本原理如下:

(1)在全频带范围[0,F]内确定搜索的频带带宽BW、频带中心频率CF的范围和迭代搜索步长step。其中,中心频率CF范围满足公式:

CF=[BW/2∶step∶F-BW/2]

(1)

带宽BW的设定应保证频带中含有所需信息,带宽较窄会导致所需信息漏失,带宽过宽会出现含有较多干扰信息。迭代搜索步长step会影响搜索的频带精度和搜索时间,迭代搜索步长step不得超过带宽BW,以确保能覆盖整个频带。step越小,搜索的频带精度越高,搜索时间越长;

(2)以BW/2为初始中心频率,对该频带信号进行带通滤波处理后,计算其包络谱峭度;

(3)迭代搜索频带中心频率CF,改变频带范围,重复(2)中步骤,直至完成全频带的迭代搜索;

(4)确定最大峭度对应的频带中心频率,由此确定具有最大冲击特性的频带范围。

1.2 MVDR方法

MVDR方法通过施加线性约束抑制其他方向波束输出,而来自期望方向的波束输出不变,对最终得到的声源功率进行峰值搜索,最大峰值对应位置即为目标声源位置。

该方法可以有效抑制其他干扰声源引起的旁瓣,得到的主瓣较窄,因此,其声源识别精度高。

假设一个线性阵列中包含有M个麦克风传感器,xi(t)表示第i个麦克风传感器接收到的信号,可将M个麦克风接收到的信号用矩阵来表示:

X(t)=[x1(t),x2(t),…,xM(t)]=A(τ)S(t)+N(t)

(2)

式中:A(τ)—声阵接收到的声音信号的导向矢量矩阵;S(t)—声阵接收到的声源信号向量矩阵;N(t)—噪声信号矩阵。

A(τ)的表达式为:

A(τ)=[1,e-j·2πfτ1,…,e-j·2πfτM-1]T

(3)

式中:f—信号的频率;τi—麦克风传感器之间接收信号的时延,i=1,2,…,M-1。

对接收到的信号进行加权求和输出,其计算公式如下:

(4)

式中:w—权矢量;wH—权矢量的共轭转置。

经计算得到的声音信号的互谱矩阵为:

(5)

MVDR方法通过最小能量准则来设计加权向量,需满足如下2个条件:

(6)

经计算得到的声源功率为:

(7)

2 方法提出

笔者提出一种基于敏感特征频带的旋转机械故障定位方法，即首先通过Protrugram方法识别含有故障信息的频带范围,然后利用MVDR方法对频带范围信号进行处理,最后识别出各声源的位置。

该方法包括选择敏感特征频带、计算声场分布和定位故障源3个部分,其具体的流程图如图1所示。

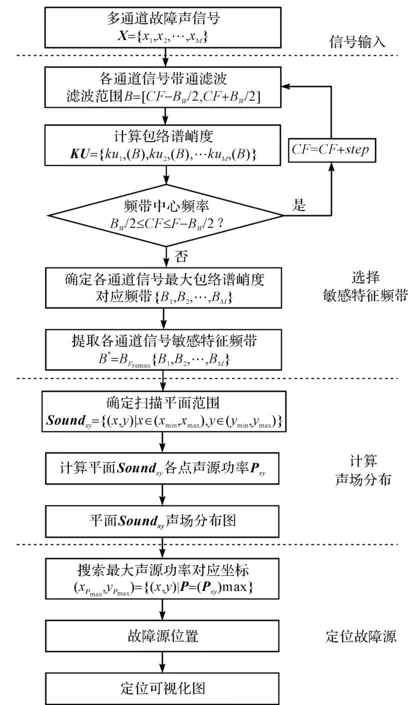
图1 方法流程图

2.1 敏感特征频带选择

对M个通道采集的声音信号X={x1,x2,…,xM}进行带通滤波处理,滤波范围为B=[CF-BW/2,CF+BW/2];计算滤波后信号的包络谱峭度,调整大小,完成全频带范围的迭代搜索,得到所有频带的包络谱峭度KU={ku1(B),ku2(B),…kuM(B),}。

考虑到轴承故障特征中可能包含有边频带信号,为了确保获得的敏感特征频带包含转子系统的大部分故障特征,笔者根据工程经验,使得带宽BW为轴承内圈故障频率的3～5倍(一般取扫描步长的整数倍[18])。由于要分别对声阵中各传感器测得信号进行处理,从中搜索最大冲击特性的频带,具有较大计算工作量,为了兼顾搜索精度和搜索时间,笔者设定step为100 Hz。

笔者确定各通道信号最大包络谱峭度对应的频带范围{B1,B2,…,BM}。

由于声阵中各传感器间距较小,从各通道信号中获得最大包络谱峭度对应的频带范围波动不大,因此,笔者选取出现频次最多的频带B*作为敏感特征频带,分别从各通道信号中提取出B*,即:

B*=BFremax{B1,B2,…,BM}

(8)

2.2 声场分布计算

根据旋转机械的结构尺寸大小,确定声场中扫描平面soundxy范围,即:

soundxy={(x,y)|x∈(xmin,xmax),y∈(ymin,ymax)}

(9)

式中:(x,y)—扫描平面内的坐标soundxy;(xmin,xmax)—x方向的坐标范围;(ymin,ymax)—y方向的坐标范围。

为了获得较高的扫描精度,笔者设定扫描步长为0.01 m。

由于B*带宽较大,直接利用其中心频率求取导向矢量,容易造成较大的误差,笔者将B*划分为多个较窄的子带,分别计算导向矢量,以降低此误差。但子带带宽小,则其中包含的有用信息也较少。因此,笔者将B*均匀划分为K个子带,设定子带宽度为100 Hz[19,20],即:

B*={Band1,Band2,…BandK}

(10)

对各子带信号进行离散傅里叶变换,得到频域信号Y:

Y={Y1,Y2,Y}

(11)

基于式(3),笔者以Y中各子带的中心频率进行相位补偿计算,得到扫描点处的导向矢量矩阵A(τ);

基于式(5),笔者计算Y中各子带信号的互谱矩阵R;

基于式(7),分别求得各子带信号的声源功率PMVDR(i)(i=1,2,…,K),最后将其进行累加,得到该点的声源功率Pxy:

(12)

根据上述方法,笔者对扫描平面内各点的声源功率进行计算,并遍历整个扫描平面,得到该平面的声场分布图。

2.3 故障源定位

在声场分布图中,根据图中峰值大小搜索得到声源最大功率对应坐标(xPmax,yPmax),该坐标即为故障源位置:

(xPmax,yPmax)={(x,y)|P=(Pxy)max}

(13)

将声场分布图的坐标系Soundxy与摄像头监控画面的坐标系Viewxy进行叠加处理,得到故障源定位可视化图H:

H=Viewxy+Soundxy=

(14)

式中:Vxy—摄像头监控画面各点的像素;Pxy—声场中各扫描点对应的功率。

3 实验及结果分析

为了验证该方法(选择敏感特征频带、计算声场分布和定位故障源)的定位效果,笔者通过转子故障模拟实验台进行故障的模拟实验,并将所得结果与采用文献[11]34-35所用方法得到的结果进行对比。

3.1 故障模拟实验台简介

转子故障模拟实验台包括电机、变速箱、转轴、联轴器、平衡盘和轴承座等部件,如图2所示。

图2 转子故障模拟实验台

实验中测得的实验台上各部件中心位置的坐标(x,y),如表1所示。

表1 实验台各部件中心坐标

3.2 实验设计

笔者设计3组不同故障类型的实验,验证该方法在不同故障情况下的定位效果。

具体实验条件如表2所示。

表2 实验组数表

实验的采样参数如表3所示。

表3 采样参数表

对于轴承类故障而言,由于现场实际的故障轴承难以获得,此处笔者依据实际条件下轴承内外圈发生断裂(或疲劳剥落)后,滚子与其表面接触产生周期性冲击信号的机理,通过在正常轴承内外圈上,以线切割的方式加工1 mm×0.5 mm的凹槽,进行故障模拟。

模拟故障部件如图3所示。

图3 模拟故障部件

为了模拟实际的应用条件,笔者将声阵放置在正对实验台1 m的位置。

声阵中包含16个PCB 130F20麦克风传感器并装有摄像头,如图4所示。

图4 矩形声阵及摄像头

声阵中各传感器坐标(x,y)如表4所示。

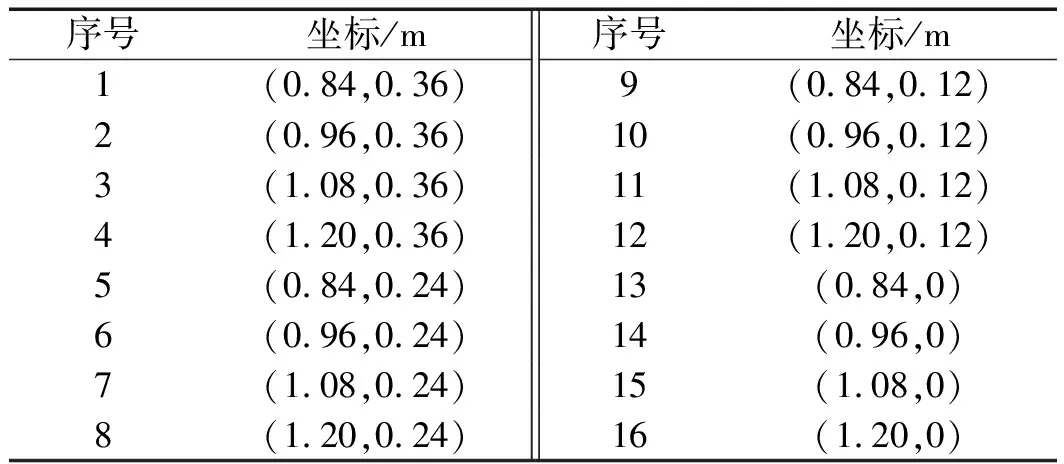
表4 声阵各传感器坐标

3.3 实验过程及结果分析

首先,利用Protrugram方法提取出敏感特征频带信号;然后,通过MVDR方法对敏感特征频带信号进行分析,计算声场分布,做出声场分布图;最后,将摄像头监控画面与声场分布图结合,从中识别最大声源位置,定位故障源位置。

3.3.1 敏感特征频带选择

根据实验条件,计算得到内圈故障轴承特征频率为156 Hz,设定带宽BW为800 Hz,频带中心频率CF范围为400 Hz～9 600 Hz。

笔者分别做出不同故障条件信号的频带包络谱峭度图,如图5所示。

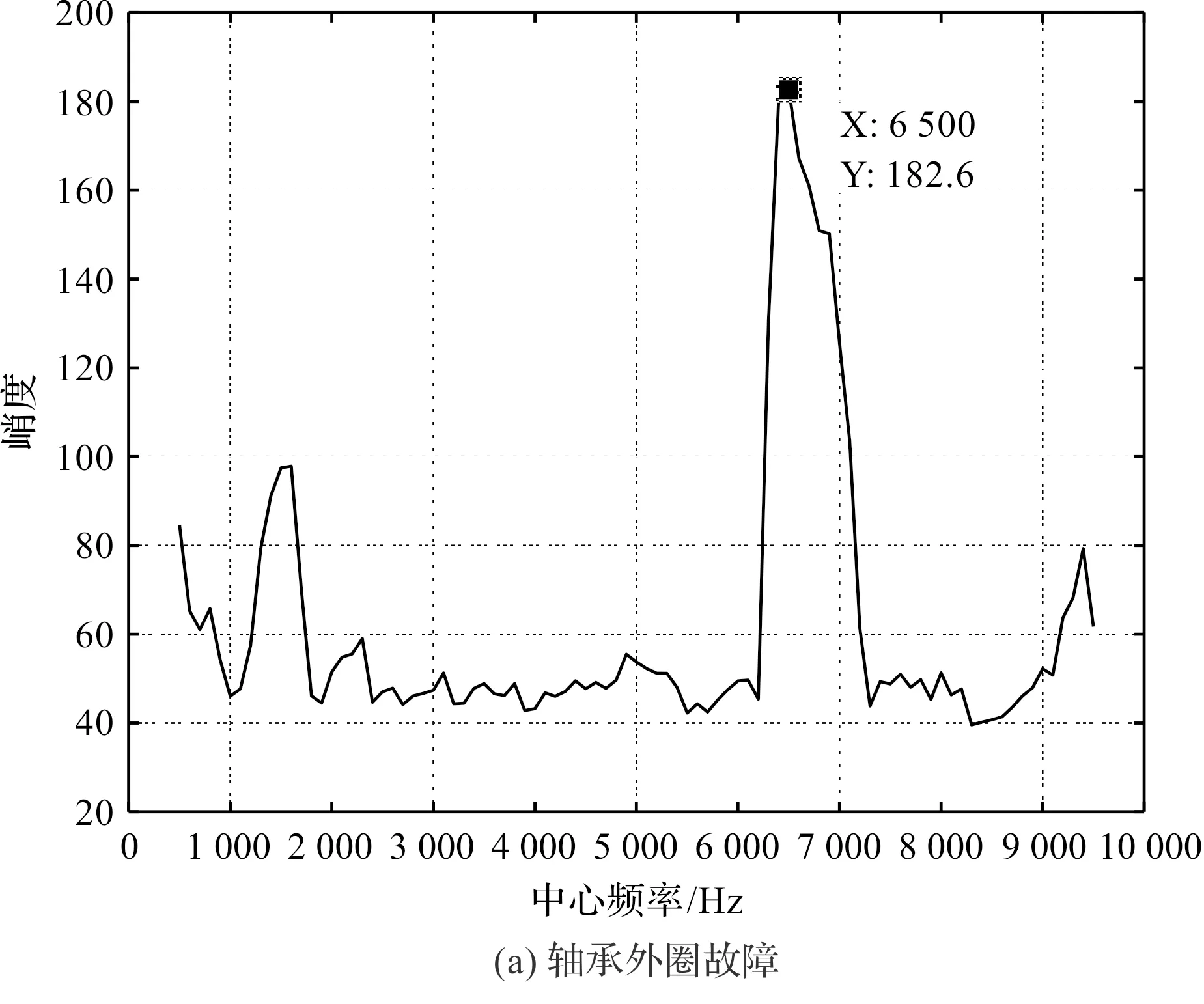
图5 不同故障条件频带包络谱峭度图

对图5进行分析,可以得到3种不同故障类型的敏感特征频带,如表5所示。

表5 不同故障类型的敏感特征频带范围

从表5中可以看出:3种不同故障类型的敏感特征频带存在一定偏差;

轴承外圈故障与轴承内圈故障的频带偏差较小,可能是由于更换轴承后再进行装配过程中的配合发生变化,导致得到的敏感特征频带发生偏移;

不平衡故障与轴承类故障的敏感特征频带存在较大偏差,原因在于平衡盘上装配有不平衡块,不平衡趋势传递至联轴器,激励产生明显噪声,该不平衡故障信号被联轴器的固有频率调制[21]。

3.3.2 声场分布计算

根据实验台结构尺寸,笔者计算该平面内的声场分布,设置扫描平面Soundxy范围如下:

Soundxy={(x,y)|x∈[0,1.4 m],

y∈[-0.7 m,-0.4 m]}

(15)

为了便于观察声源的功率大小,笔者以三维形式展示3种不同故障类型的声场分布图,如图6所示。

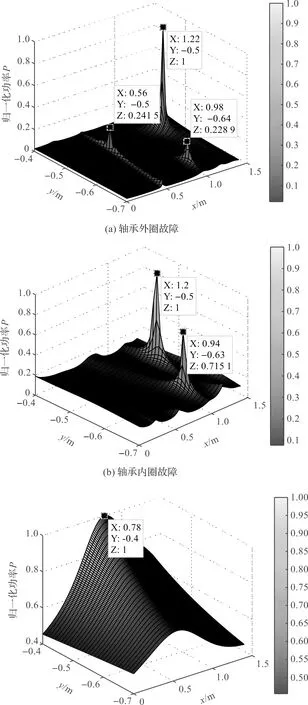
图6 不同故障条件声场分布图

由图6可知:经搜索得到3种不同故障条件下声源最大功率对应坐标,该坐标即为估计出的故障源所在位置。

3.3.3 故障源定位

3种不同故障源定位结果,其坐标如表6所示。

表6 3种不同故障条件的故障源定位结果

笔者做出3种不同故障条件的定位可视化图,如图7所示。

图7 不同故障条件定位可视化图

从图7(a)中可以看出:轴承外圈故障条件下的声场中存在3个声源,分别位于变速箱、靠近实验台底部和2#轴承座位置;最大功率声源位置靠近故障轴承处,故障源定位结果符合实验条件;在变速箱处存在功率较小的声源,是由于变速箱在正常运行过程中齿轮间啮合运转产生的声音,与实际实验情况相符;在靠近实验台底部存在声源,可能是由于噪声传递至实验台底部发生反射或其他气动性噪声;

从图7(b)可以观察到:轴承内圈故障条件下的声场中存在2个声源,声源最大功率位置对应故障轴承处,说明轴承发生故障,还存在由经实验台底部反射的噪声或气动性噪声;

从图7(c)中可以观察到:不平衡故障条件的声场中存在1个明显的声源,该声源中心位于靠近联轴器位置,由此认为联轴器处存在故障。与轴承类故障的声源主瓣宽度相比,不平衡故障声源主瓣宽度明显更大,这是由于波束形成方法在低频段定位分辨率较低。

当转轴发生不平衡时,不平衡趋势也会传递至1#轴承座和2#轴承座位置,激励产生噪声,为了辅助验证该定位方法的准确性,结合轴承发生故障时敏感特征频带范围在6 000 Hz～7 500 Hz内波动的特点,笔者对不平衡故障条件6 000 Hz～7 500 Hz频段的信号进行定位计算,并做出其声场分布图及定位可视化图,如图8所示。

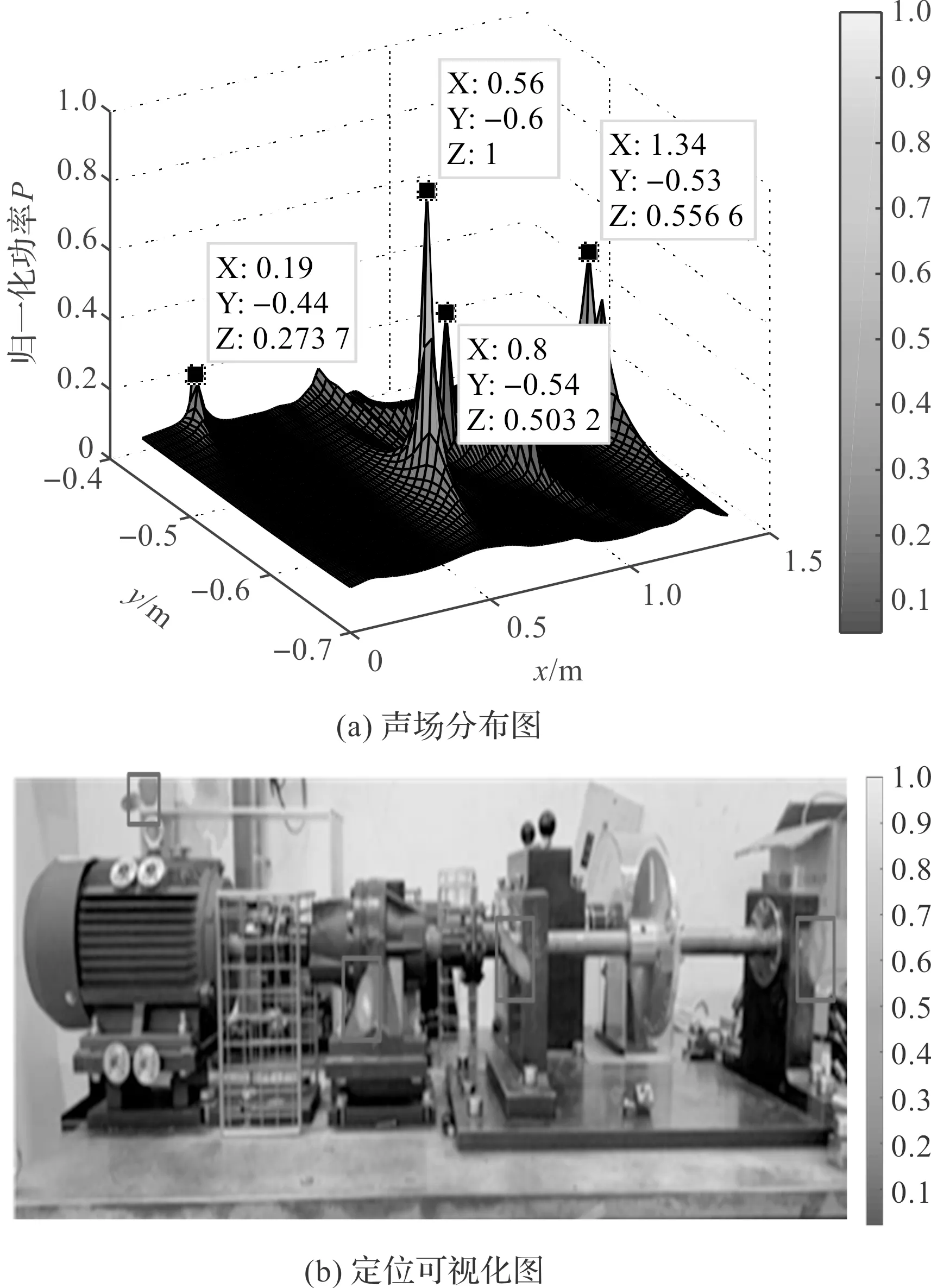
图8 不平衡故障信号6 000 Hz～7 500 Hz定位结果图

从图8中可以观察到:声场中存在4个声源,分别位于电机、变速箱、1#轴承座和2#轴承座位置,且变速箱和电机在正常运行过程中存在噪声,变速箱噪声较大,电机噪声较小,符合实际实验情况;

靠近两轴承座位置存在声源,说明轴承座位置有故障,两轴承座到平衡盘的距离相同,产生不平衡趋势相近,因此,声源功率大小相差不大。两轴承座的声源功率小于变速箱位置的声源功率,可能是因为不平衡趋势不明显,导致在轴承座位置产生的激励较小。

上述结果进一步验证了定位方法的准确性。但是对于不平衡故障而言,利用轴承故障敏感特征频带进行定位分析,会导致识别结果中出现过多声源,较难区分出主要故障源位置,容易和轴承类故障混淆;而直接对冲击更明显的不平衡故障敏感特征频带进行分析,则更易识别出不平衡故障位置。

3.4 方法对比分析

笔者对采用新方法和对比方法所获得的定位结果进行,如表7所示。

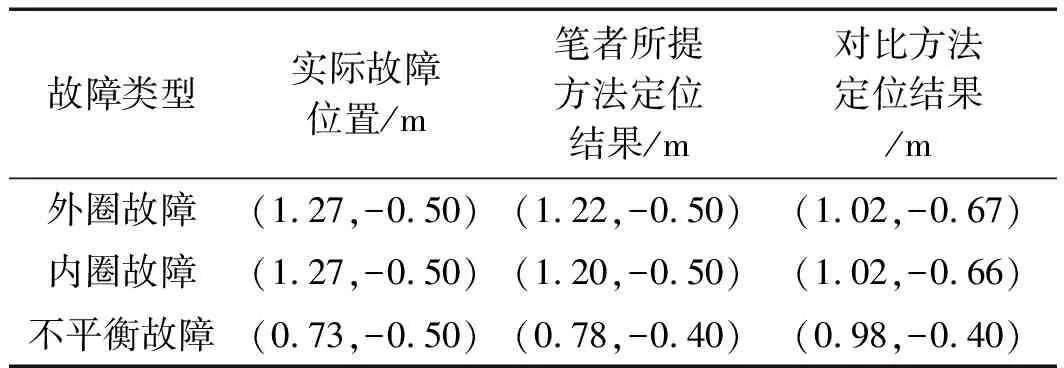
表7 故障源定位结果表

从表7中可以看出:笔者所提出方法得到的x方向和y方向误差均不超过0.10 m;对比方法在x方向和y方向的定位误差均大于0.15 m。

通过上述实验结果可知:笔者所提方法的定位误差明显小于对比方法,定位效果更好。

该方法依据旋转机械的故障特性,准确选取了含有故障信息,且位于高频段的敏感特征频带,通过对该频带信号进行定位分析,准确识别出主要故障源位置,解决了仅依据专家经验选取一定频率范围信号,导致故障信息漏失、故障源定位误差较大的问题。同时,该方法还能识别出故障特征频率位于低频段的故障源,以免直接对全频带信号进行分析,带来定位精度低,且干扰声源多的问题。

此外,该方法通过线性约束有效抑制了旁瓣干扰,构建了更为清晰的声场,具有更好的故障源识别效果。

上述实验结果及分析表明:笔者所提方法合理利用了波束形成方法中,高频段定位精度高的优势,可以有效地识别故障源的位置,具有较高的定位精度。

4 结束语

在基于声阵的旋转机械故障监测过程中,存在故障源定位不准确的问题,为此,笔者提出了一种基于敏感特征频带的旋转机械故障源定位方法。

笔者首先采用Protrugram方法,提取了敏感特征频带信号,然后利用MVDR方法计算了声场分布,并确定了故障源位置,最后设计了故障模拟实验,对该方法的可行性进行了验证。

研究结论如下:

(1)选取旋转机械故障声信号中调制后的高频敏感特征频带信号进行了定位分析,对于故障特征频率位于低频段的故障源,该方法可以有效识别故障源位置,实现了故障源定位的可视化;

(2)针对旋转机械故障特性,选取含有目标信息的频带进行了定位分析,对于其他类型机械故障源定位具有一定的借鉴意义。

在后续研究中,笔者将在实际运行工况下,验证所提出方法在泵、风机等较为复杂结构机械中的定位效果,并通过多组数据的定位分析,以此来排除由于环境和工况等因素所引起的短时随机性异响干扰。