水下圆柱壳自由场声辐射特性的获取
林伟,夏茂龙,孟春霞,黎胜*
1大连理工大学船舶工程学院工业装备结构分析国家重点实验室,辽宁大连116024
2水下测控技术重点实验室,辽宁大连116013
0 引 言
水中目标的声特性测量对目标特性的设计、性能评估、识别和控制等具有重大意义。针对水中目标辐射噪声的测量,最适合的条件是水下自由场。为满足水下自由场条件,测量一般在室内消声水池或者天然水域(如大的湖泊、大海等开阔水域)中进行。但在消声水池中难以实现大型结构的测量和目标的低频测量,而在天然水域进行测量容易受到环境和气候的影响,难以获得理想的自由声场。因此,实现在复杂声场测量条件下获取水中目标自由场的声辐射特性,突破测试环境对水中目标声特性测量的限制,能够极大地提高目标声特性的测量能力和水平,大幅降低测试费用,具有重要意义和实际工程价值。
对于空气中目标的自由场声特性的获取,国内外学者开展了许多研究。基于空间傅里叶变换的声场分离技术[1]是广泛应用于近场声全息技术(Nearfield Acoustic Holography)[2]中的一种声场分离技术,该方法能够将目标声源的辐射声场从干扰声源、反射、散射等复杂声场中分离出来;但受方法本身限制,其只能用于平面、柱面、球面等规则测量面,无法分离不规则测量面[3]。Langrenne等[4]提出了基于边界元法的声场还原技术,该技术利用边界元法还原声场,能应用于任意形状的测量面;但是基于边界元法的声场还原技术只验证了场点声压、声功率等方面的还原效果,未研究指向性等特性的还原效果。毕传兴等[5]提出了采用球面波叠加法还原自由声场的方法,较好地解决了球形声源的声场分析问题,但该方法只适用于球形声源。基于等效源的自由场还原方法[6]实现了在噪声环境中对目标声源辐射声场的准确重建,但这些声场分离技术很少用于获取水中目标的声特性,比如,典型的水下圆柱壳模型的自由场声特性获取就较少采用这些技术。
在进行水下目标的声特性测量时,海面、海底和水中其他噪声源会对其产生极大的干扰,需要利用声场还原技术消除测量干扰,还原目标的自由场声学特性。而基于边界元的声场还原方法只需要测量面上的声压,来进行声场分离,对测试环境要求较低,同时具有较高的精度。因此,本文拟采用基于边界元法的声场还原技术,来解决以海面或海底为边界且有噪声源干扰下的半空间中水下目标自由场声辐射特性的获取问题,将以圆柱壳为例,分别还原圆柱壳只在海面/海底影响下或同时受海面/海底以及外部噪声源影响下的自由场声辐射特性。
1 基于边界元法的声场还原技术
基于边界元法的声场还原技术是将复杂环境下的声场分为向外和向内的声场,向外声场由自由场声场和向内声场作用在目标声源表面散射形成的声场组成。因此,将复杂环境下测得的场点声压分离出向外的声压,向外的声压再分离出散射声压,就能够还原目标的自由场声压。
水下测量时目标声源、边界及外部声源分布如图1所示。其中:边界Γ1和边界Γ2之间的空间为V;Γ1为目标声源S0的表面,其法向为;Γ2为声场边界,其法向为;S为积分面,其法向为ns;将空间V分为V1和V2;Q(r')为外部噪声源强度;s'为边界上的点。

图1 声场示意图Fig.1 Schematic diagram of sound field
空间V中,任意一点的声压可以表示为[7]
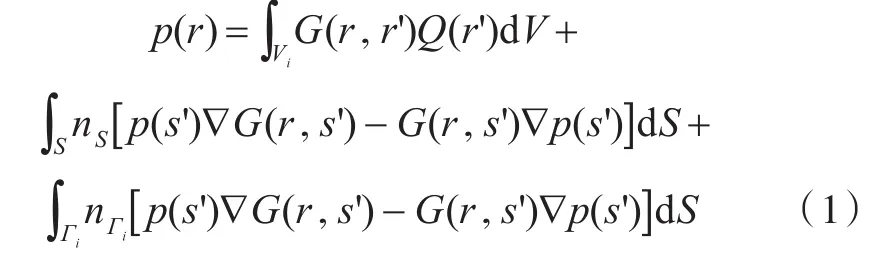
式中:i=1或2;r为场点位置;r'为外部噪声源位置;p(s')为s'处的声压;∇p(s')为s'处的声压梯度;G(r,r')为自由场的格林函数;∇G()为自由场的格林函数梯度;自由场的格林函数表达式为
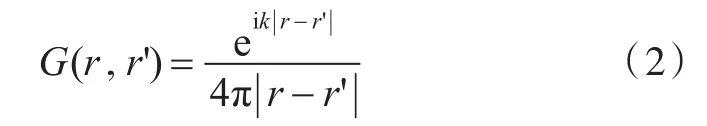
式中:k为波数;e为自然常数;i为虚数单位。
场点声压分解为向内和向外两部分,表示为
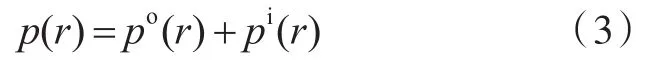
式中:pi(r)为向内声场,Pa,包括外部噪声源辐射声场和海底或海面边界Γ2反射声场;po(r)为向外声场,Pa,由自由场声场pf(r)和向内声场作用在目标声源表面Γ1上的散射声场ps(r)叠加形成。

1.1 声场分离
利用2层封闭的测量面包裹目标声源,这2层测量面网格相似、节点数相同且距离较近,定义2层测量面中间位置处的面为积分面S。利用测量面上各测点的声压值,分别使用平均法和有限差分法近似计算出中间积分面S上s'处的声压p(s')和法向速度vn(s')[8]为:
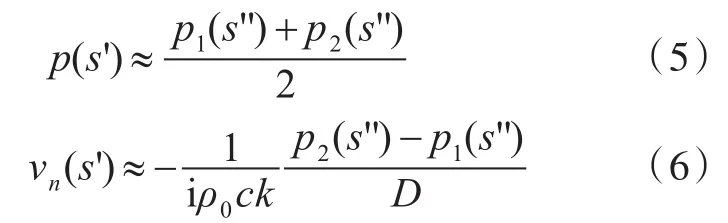
式中:p1(s'')为内侧测量面节点的声压,Pa;p2(s'')为外侧测量面节点的声压,Pa;D为内、外测量面之间的距离,m;ρ0=1 000 kg/m3,为水的密度;c=1 500 m/s,为水中声速。积分面S上的p(s')和vn(s')分离得到向外声压po(r)和向内声压pi(r)。
对于积分面S的内场问题,可将式(1)简化为
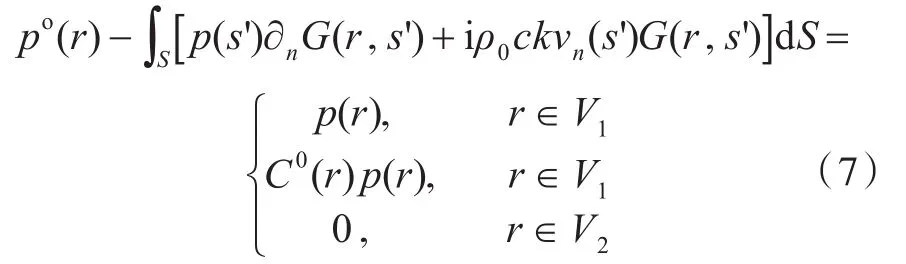
式中:∂n为沿着法向求偏微分;C0(r)为系数,其计算公式为
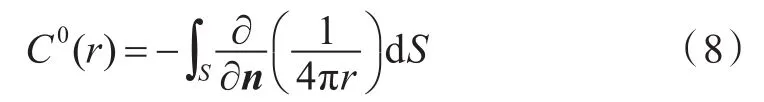
式中,n为法向。
当积分面S上的声压和声压梯度已知时,r∈S,向外声压可以根据式(7)求出:
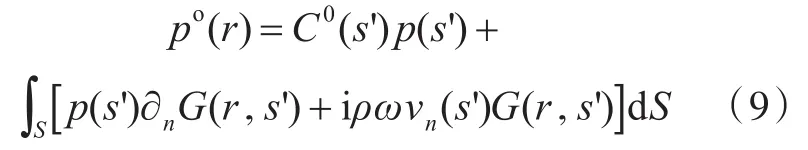
式中,ω为圆频率。
在求解散射声场之前,需要先计算作用在目标声源上的入射波。对于积分面S的外场问题,通过式(1),可以得到
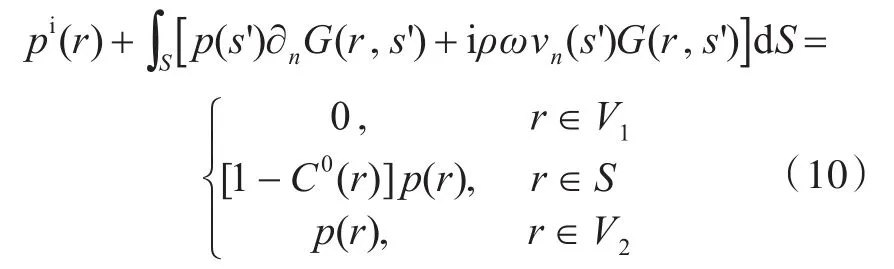
根据式(10),当r∈V1时,
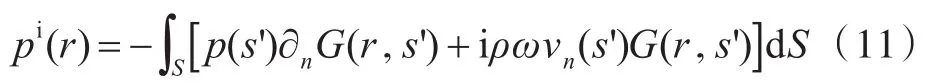
计算散射声场时,为简化计算,假设目标声源S0静止 (pf(r)=0),同时结构是刚性的,因此vn(r)=0。对于表面Γ1,利用边界元的散射公式求解散射声场,在入射波作用下的散射声场可以表示为[9-10]

式中:C0'(p)为系数;pb(s)为作用于目标声源表面的散射声压。作用在积分面S上的散射声场可以表达为
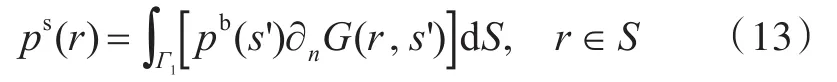
结合式(9)、式(11)、式(12)和式(13),可以得出
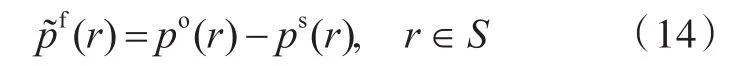
1.2 边界元离散
进行数值计算时,需要进行边界离散。边界离散后,式(7)中S面上向外的声压可以表示为

向内的声场根据式(11)可由以下公式求取:
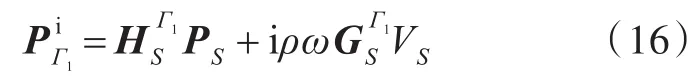
根据式(12)进行边界离散后,封闭声压可以表示为
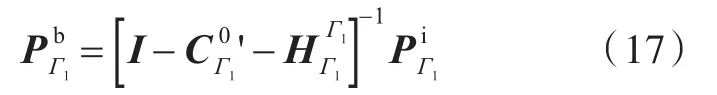
采用边界元法时存在不唯一解的情况,可以利用CHIEF点法[11-12]克服这一缺陷,求取正确解。根据式(13)的离散边界,S面上的散射声压可以表示为

2 复杂环境中水下目标自由场声辐射特性的获取
2.1 海面/海底影响下的声源自由场声特性获取
测量环境示意图如图2所示,边界元模型如图3所示。海水和空气分界面近似为自由边界,这时边界上的声压等于0;硬质海底属于绝对硬边界类型,声波不能进入海底,此时边界上介质质点的法向振速为0[13]。在垂直于x轴方向,距离原点1 m处设置一个无限大的刚性表面或者自由表面,模拟海底或海面对声场的影响。利用一个在水中长度l=1.2 m,轴线与z轴方向平行,半径为0.162 5 m,中心位于原点的圆柱壳体结构。积分面是高1.6 m,长和宽均为0.6 m,中心位于原点的曲边长方体。设置圆柱壳在xy平面上的π/4弧度部分以0.003 m/s的法向速度振动。在积分面两侧分别设置一个测量面,测量面与积分面之间的距离均为0.03 m。
图2 计算模型示意图Fig.2 Schematic diagram of the calculation model

图3 边界元模型Fig.3 Boundary element model
声源通常可以等效为一定数目的单极子源和偶极子源,当考虑外部噪声源对声场的影响时,分别在 (0.7 m,0 m,1 m)和 (0.7 m,0 m,-1 m)处设置强度为400 kg/s2的单极子源,以及在x,y,z方向强度均为(200+150i)kg/s2的偶极子源,以模拟外部噪声干扰。基于边界元的声场还原方法要求外部噪声源处在测量面之外,向内辐射声场,该方法无法分离背景噪声。通常,水中的参考声压为10-6Pa,参考声强为10-18W/m2[14]。
定义声功率∏的计算式为
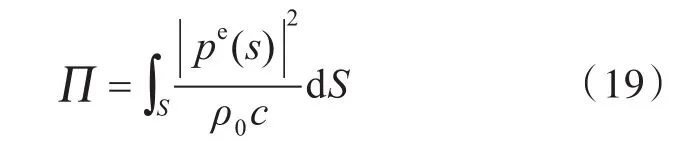
式中,pe(s)为计算声场在该点的声压值,Pa。例如,当计算还原声场声功率时,pe(s)=f(r)。
在还原声场之前,需要初步验证理论方法的正确性和网格的收敛性。将复杂声场中测量面上直接测量得到的声场定义为总声场,测量面上背离目标声源方向的声场定义为向外声场,指向目标声源方向的声场定义为向内声场,经过声场还原技术得到的声场定义为还原声场,自由场中得到的声场定义为自由场。当目标声源位于自由场时,向内的声场和散射声场不存在,所以向外声场等于自由场。图4给出了当内部圆柱壳划分为1 028个三角形线性单元、测量面分别划分为912和3 632个单元时各声场声功率级随kl(k为波数,l为声源的特征长度,l=1.2 m)的变化趋势。当测量面划分为912个单元时,向外声场与自由场的声功率级最大差值不到3 dB,但向内声场与向外声场的最小差值为14.7 dB,向内声场相较于向外声场不能忽略,无法满足计算精度要求;当测量面划分为3 632个单元时,向外声场与向内声场的声功率级相差30 dB以上,可以忽略。同时,向外声场与自由场的声功率级完全一致,符合理论分析的结果并满足计算精度要求。

图4 自由场中积分面S上的声功率级Fig.4 Calculation result of the sound power level on the integral plane S in free-field
当考虑海底对声场的影响时,其声场的分布情况和还原结果如图5所示。当kl<2.5时,由图6可知,向外声场、还原声场和自由场的声功率级基本重合。究其原因,在低频时,波长远比目标声源尺寸大,散射可以忽略。所以当频率较低时,即使忽略散射声场,也可以获得较好的还原效果。随着频率的增加,特别是当kl>4.5时,由图7可见,入射波作用在目标声源上产生的散射不能忽略。但还原声场与自由场的声功率相对误差小于1%,还原效果很好。
同理,当考虑海面对声场的影响时,还原结果如图8所示,上述结论同样成立。

图5 当考虑海底的影响时积分面S上的声功率级Fig.5 Sound power level on the integral surface S considering the influence of seabed
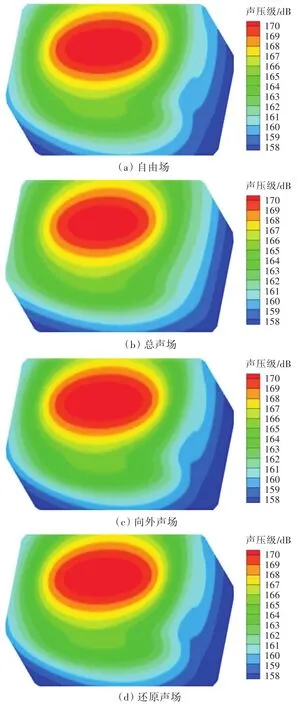
图6 f=360 Hz(kl=1.81)时积分面S上的声压分布云图Fig.6 Sound pressure contours on the integral surface S with f=360 Hz(kl=1.81)
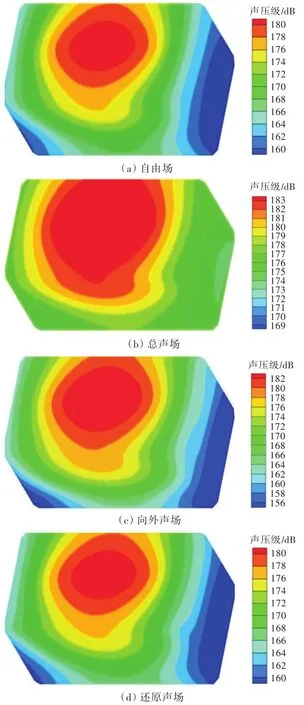
图7 f=1 140 Hz(kl=5.73)时积分面S上的声压分布云图Fig.7 Sound pressure contours on the integral surface S with f=1 140 Hz(kl=5.73)
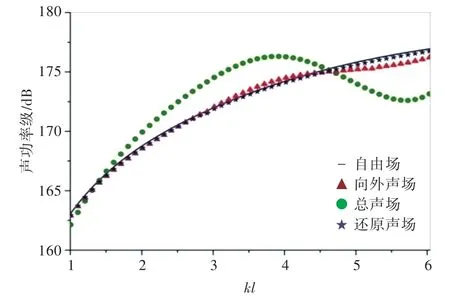
图8 考虑海面影响时积分面S上的声功率级Fig.8 Sound power level on the integral surface S considering the influence of sea surface
2.2 海面/海底和外部噪声源干扰下声源自由场声特性的获取
由图9可见,当存在外部噪声源时,由外部声源引起的散射声场部分增大,即使kl很小,散射声场也不能再忽略;因此,还原声场时必须考虑散射声场的影响。而还原声场的声功率级则与自由场的保持一致。由图10和图11可知,当存在外部噪声源时,总声场、向外声场与自由场的场点声压分布明显不同,而还原声场与自由场的场点声压分布则基本一致。
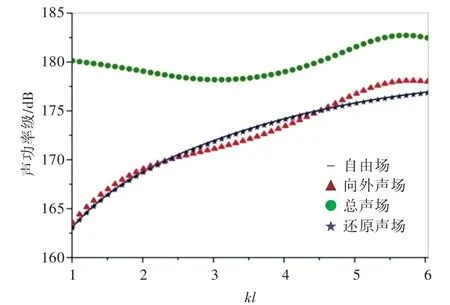
图9 考虑海底和外部噪声源影响时积分面S上的声功率级Fig.9 Sound power level on the integral surface S considering the influence of seabed and external noise sources
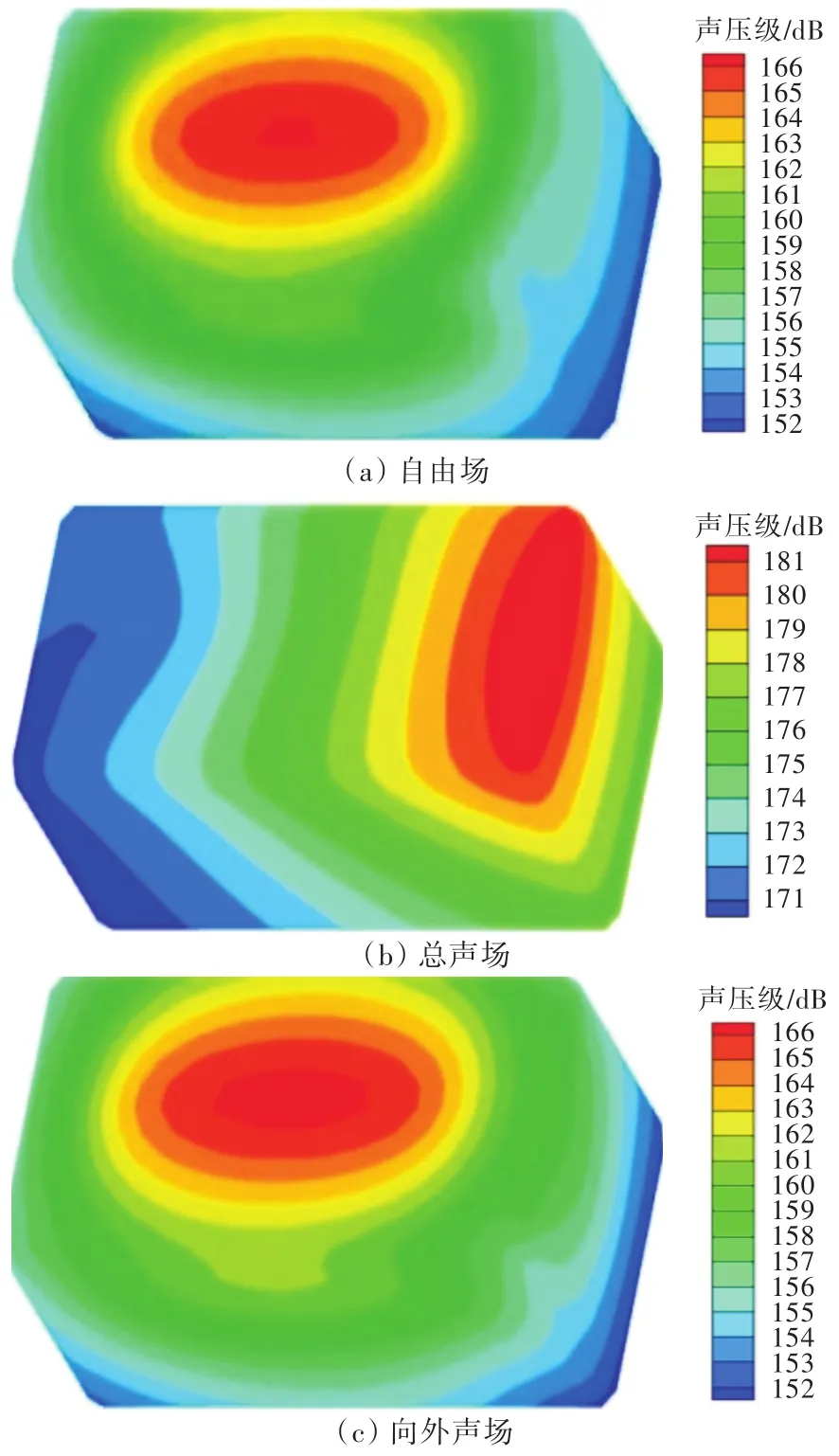
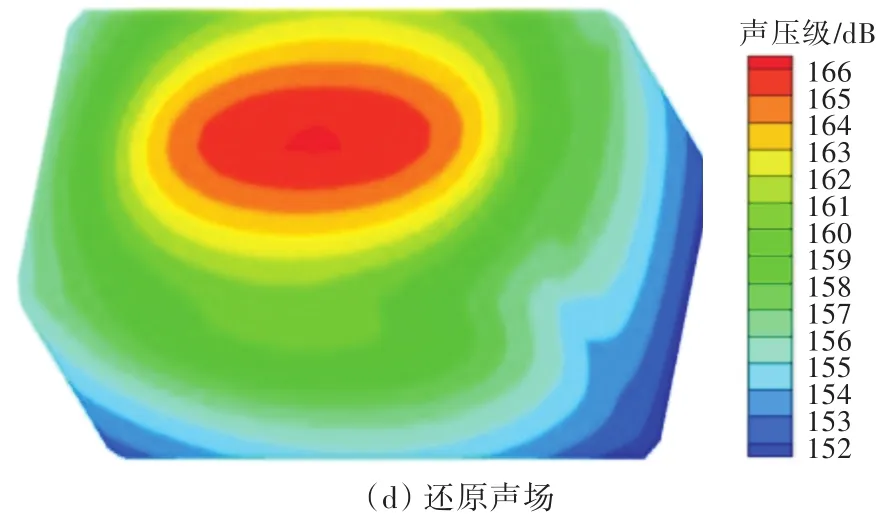
图10 f=200 Hz(kl=1)时积分面S上的声压分布云图Fig.10 Sound pressure contours on the integral surface S with f=200 Hz(kl=1)
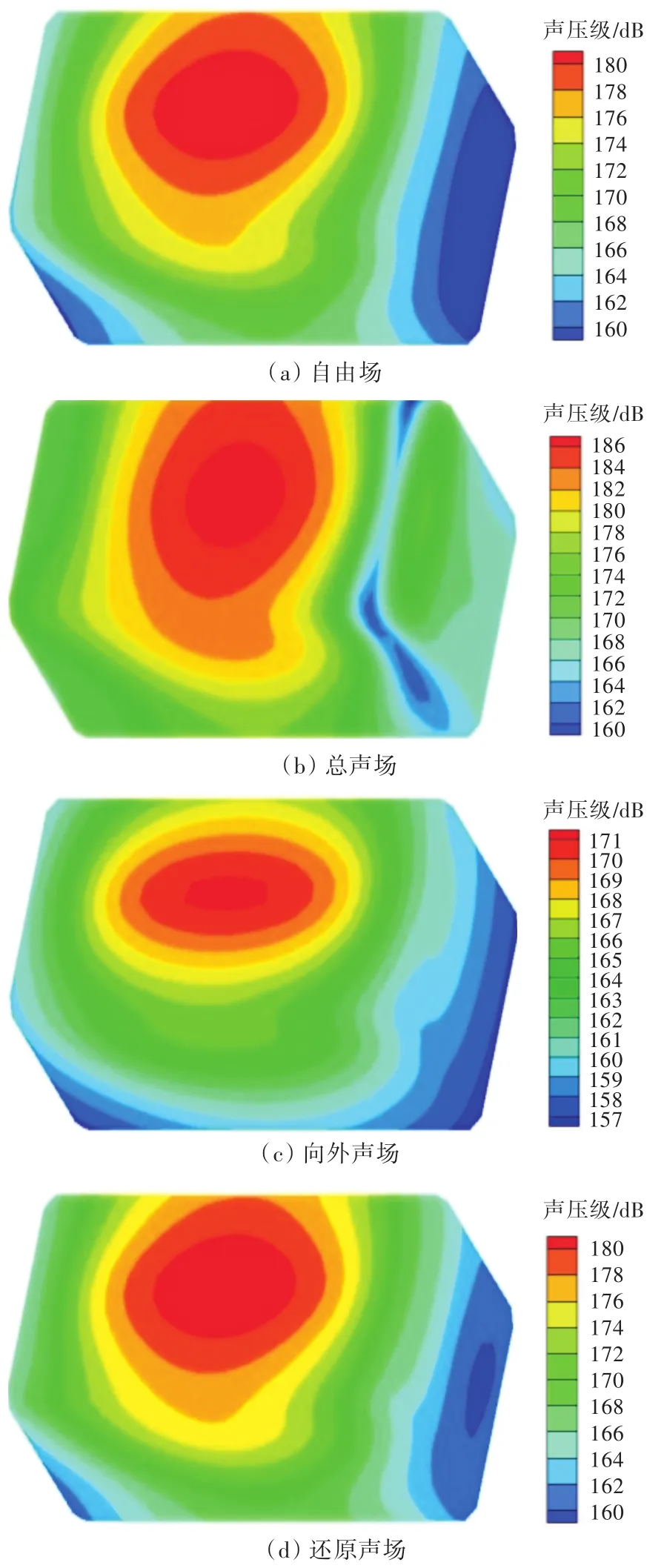
图11 存在外部噪声源时f=1 140 Hz(kl=5.73)在积分面S上的声压分布云图Fig.11 Sound pressure contours on the integral surface S with f=1 140 Hz(kl=5.73)with external noise disturbance
当考虑外部噪声源和海面对声场的影响时,声场还原结果如图12所示。由图可见,声场还原规律与上述结论一致。可见,基于边界元法的声场还原技术能够在海底/海面和外部噪声源的影响下,准确得到目标声源的自由场声功率特性和声场分布,即

式中,E为相对自由场声压的相对误差的平方对测量面的积分,即相对误差的平方和。
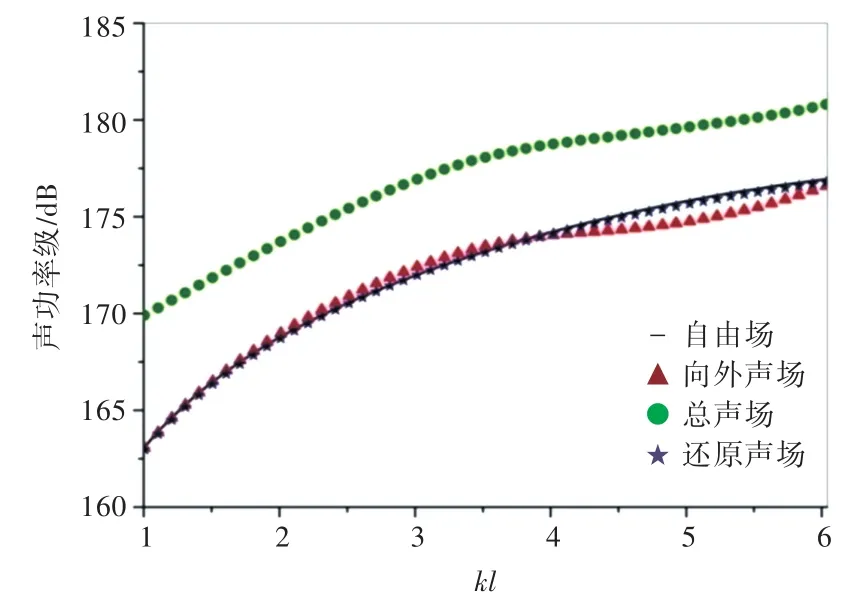
图12 考虑海面和外部噪声源影响时积分面S上的声功率级Fig.12 Sound power level on the integral surface S considering the influence of seabed and external noise sources
图13和图14分别为考虑海底、海面和外部噪声源干扰时,总声场、向外声场和还原声场相对自由场相对误差的平方和。还原声场较自由场声场的相对误差很小,保持在0.3%以下,证明该方法的声场还原效果很好。
以自由场声场为参考对象,比较在有外部噪声源干扰时,以刚性表面为边界的半空间内结构还原声场的指向性。选定频率为1 200 Hz,且圆心位于原点的半径r'=0.5 m的xy平面内圆周上的场点。根据图15所示,总声场和向外声场的指向性与自由场的指向性有明显差别,但还原声场的指向性与自由场的指向性一致。这证明基于边界元法的声场还原方法不仅可以得到与自由场声场声功率相同的还原声场,而且两者的指向性保持一致。
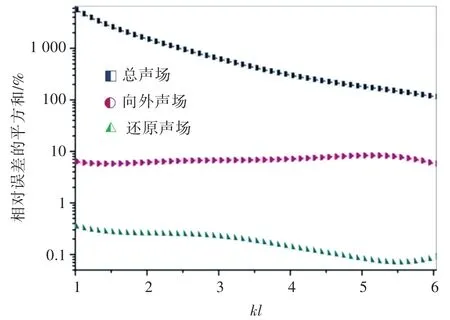
图13 考虑海底和外部噪声源影响时与自由场声场的相对误差的平方和Fig.13 Mean quadratic errors relative to the free sound field considering the influence of the seabed and external noise sources
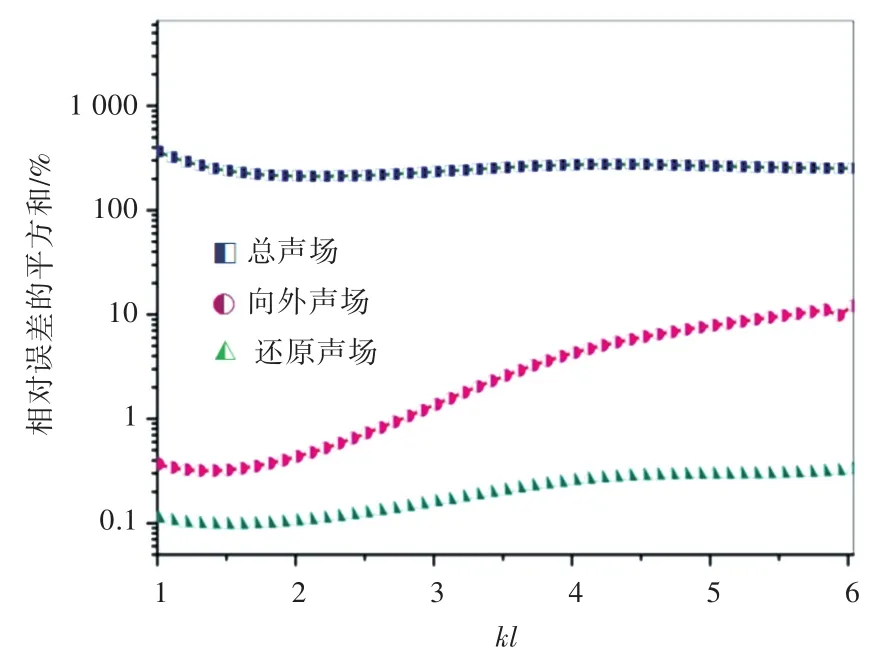
图14 考虑海面和外部噪声影响时与自由场声场的相对误差的平方和Fig.14 Mean quadratic errors relative to the free sound field considering the influence of sea surface and external noise sources
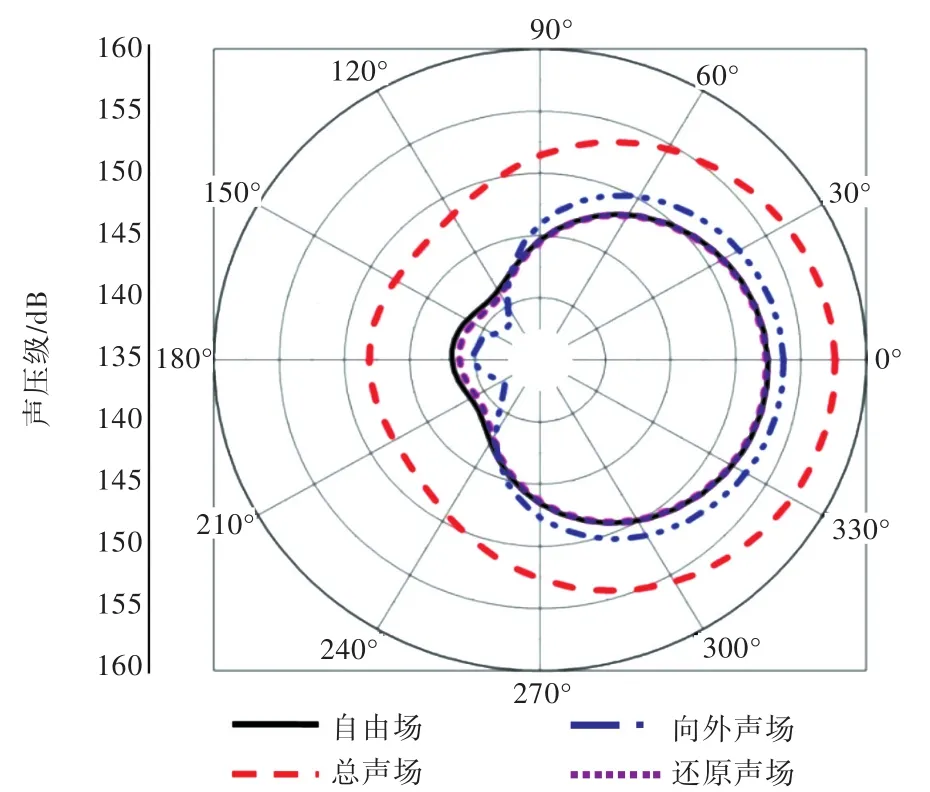
图15 f=1 200 Hz时考虑海底和外部噪声源影响时的指向性图Fig.15 Directivity pattern considering the influence of seabed and external noise sources with f=1 200 Hz
3 结 语
本文利用基于边界元法的声场还原技术还原了半空间声场,解决了水中目标在海底、海面和外部噪声源影响下的自由场声学特性的获取问题。以圆柱壳为例,分析数值仿真结果发现:当没有噪声源干扰时,仅考虑海底或海面的影响且频率较低时,散射声场基本可以忽略,向外声场、还原声场与自由场的声场特性(如声功率级和场点声压分布等)基本一致;随着频率的增加,散射声场无法忽略,向外声场与自由场之间的声场特性差异逐渐增大,但还原声场与自由场的声场特性仍然保持一致。考虑海底、海面和外部噪声源的影响后,即使频率很小,散射声场也不能忽略,但基于边界元法的声场还原技术能有效消除边界和外部噪声源的干扰,还原声场和自由场的声场特性,如声功率级、场点声压和指向性等保持一致,相对误差很小。因此,当测量水下结构物的辐射噪声时,不需要将结构置于消声水池中,即使在近海区,在有边界和外部噪声干扰的情况下,利用基于边界元法的声场还原技术也可准确获得结构的自由场声学特性。同时,该方法还可以与近场声全息技术结合,将目标声源辐射声场从含有干扰声源、反射、散射等的复杂声场中分离出来,准确识别目标的声源特性。

