基于重叠网格的船模停船操纵CFD数值模拟

孙晨光 ，王建华 ，万德成*

1上海交通大学船舶海洋与建筑工程学院，上海200240

2上海交通大学海洋工程国家重点实验室，上海200240

3高新船舶与深海开发装备协同创新中心，上海200240

0 引 言

近年来，为降低海运成本，提高运输效率，船舶正向大型化方向发展。随着港口与航道逐渐变得拥挤，船舶因相撞而发生的海损事故频繁发生。另外，船舶的大型化使得船体本身的运动性能降低，无论是转向能力还是速度调节能力，都有一定幅度的下降，导致操作不便。为确保船舶在航行中的安全，需要对船舶的停船性能进行更为深入的研究。

对于一般大型船舶在通常情况下的停船操纵动作而言，制动方式仍以倒车制动最为普遍。船舶在前进中或在静止状态下使用螺旋桨倒车时，在船尾一些横向力的作用下，会使船艏或左或右偏转，这种现象便是倒车效应［1］。具有良好停船性能的船舶，应当在实施停船操作后具有相应于其船长的最小停船距离（冲程）、最小偏航量（停船横距）和最小偏航角［2］。

倒车停船是船舶操纵与避碰的一种重要手段。1993年，国际海事组织（IMO）通过了《船舶操纵性暂行标准》，其中就对停船性能提出了明确要求。2002年底，IMO完成了对《船舶操纵性暂行标准》的修改和补充，其中就包括对停船性能的补充要求，从此，《船舶操纵性标准》正式颁布［3］。

倒车停船运动一直是船舶操纵领域的一个重要研究课题，国内外不少学者针对船舶的倒车停船运动问题进行了若干研究。传统的船舶停船操纵数值研究主要是基于约束船模试验［4］构建停船操纵数学模型，然后分离出相关水动力导数，通过数值模拟预报船体水动力，进而得出停船操纵中所需要的水动力导数值，最后，基于上述参数计算模拟出船舶的运动响应。Chislett和Smitt［5］通过约束船模试验，确定了倒车横向力的存在。刘正江［6］提出了倒车横向力（矩）的回归公式，其预报结果与实船结果基本吻合，但该文没有考虑船舶在吃水船长比较小、螺旋桨浸深较小时的倒车横向力（矩）。赵月林和古文贤［7］对浅水中的倒车停船性能进行了预报，并对停船方法予以了探讨。闫伟［8］针对大型船舶在浅水域的操纵性能进行了研究。张玉喜等［9］在 Fujii等［10］的研究基础上，对狭窄水道中航行船舶的间距控制进行了研究。张强等［11］在近年来有关船舶操纵性研究成果的基础上，结合有关模型参数和流体动力学导数的不同求取方法，给出了适用于船舶港内操纵的、考虑右旋单桨倒车特性的船舶港内操纵模型。上述学者都是通过公式计算来间接得到停船操纵的相关参数，无法直观反应出船舶停船过程中的船体受力和流场信息，不能深入研究现象产生的机理，从而也就无法为初期船舶设计和停船操纵方式的选择提供有力的建议。

目前，有关倒车停船操纵的研究主要采用约束模参数与操纵性数学模型，这种方式无法研究螺旋桨倒车过程中的尾流场以及船、桨之间的相互作用。因此，采用CFD方法对倒车停船的操纵过程进行数值模拟具有重要研究意义。通过重叠网格技术求解船舶大幅度运动是目前主流的方法。Sakamoto等［12］采用船舶水动力学软件CFD Ship-Iwoa Ver.4对标准船模DTMB 5512的裸船体进行了平面运动机构（Planar Motion Mechanism，PMM）静态和动态试验的数值模拟，并进行了相应的验证。Carrica［13］通过求解非定常RANS方程，采用重叠网格方法对DTMB 5512船模进行了回转运动和Z型操纵试验的数值模拟。Mofidi等［14］采用重叠网格技术，对船、桨、舵全耦合条件下的KCS船模Z型操纵试验进行了数值模拟，其中关于船、桨、舵的耦合计算采用了一套多级物体运动求解模块。Yoshimura［15］对浅水中的船舶操纵进行了数值建模和计算，其结果与试验结果吻合较好。上海交通大学万德成教授课题组基于开源CFD软件OpenFOAM和重叠网格技术，开发了针对船舶与海洋工程结构物大幅度运动条件下的水动力学求解器 naoe-FOAM-SJTU［16］，在海上浮式结构物、标准船模等在波浪上的运动和船舶操纵性数值模拟等方面均取得了一定的成果。使用该求解器，王建华等［17］实现了全附体ONRT船模在波浪中自航的数值模拟；吴建威等［18］成功预报了螺旋桨敞水性能；尹崇宏等［19］模拟了实尺度下VLCC船模的航行阻力，其结果与实验结果吻合良好；罗天等［20］模拟了KCS船型的横摇运动，并对粘性效应进行了分析。

本文将使用基于重叠网格技术的naoe-FOAM-SJTU求解器，针对浅水与深水这2种工况，对船、桨配合下的倒车停船操纵进行CFD数值模拟，预报停船过程中的停船纵距、横距等参数，细致分析并对比2种工况下船舶操纵过程中的船体表面压力以及船周流场情况，以为停船问题在船舶前期设计和操纵方式的选择方面提供参考。

1 数值方法

1.1 流场计算

使用上海交通大学自主开发的naoe-FOAM-SJTU求解器进行数值计算求解。流体控制方程为非定常两相不可压缩的RANS方程：

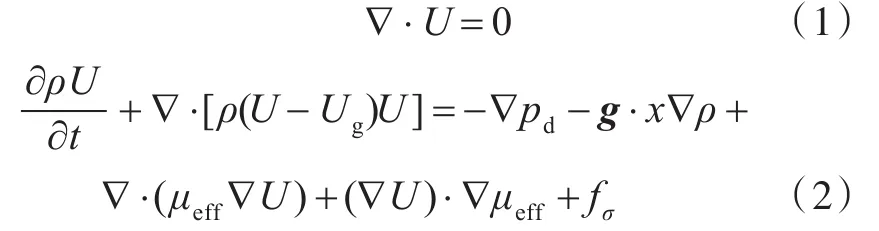
式中：x为网格节点的位置；t为时间；U为速度场；Ug为网格的移动速度；pd为动压力，即总压力与静水压力值差；ρ为液体密度；g为重力加速度向量；μeff为有效动力粘性系数；fσ为表面张力项。

本文使用SSTk-ω湍流模型实现RANS方程的闭合，其中k为流体质点的湍动能，ω为特征耗散率。这样的湍流模型既不受自由面的影响，也能保证在壁面处求解的精确性和可靠性。同时，本文还采用带有人工可压缩项的流体体积（VOF）法处理自由液面［21］，其输运方程定义为

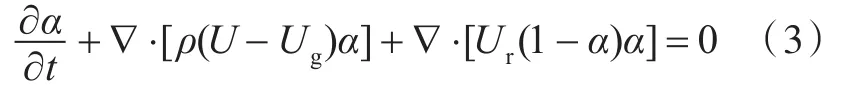
式中：Ur为用于压缩界面的速度场；α为两相流体积分数，其定义为

本文计算中的RANS方程和VOF方程均采用有限体积法进行离散，对于离散后得到的压力速度耦合方程，采用PISO（Pressure-Implicit-Split-Operator）算法［22］进行循环迭代求解。

1.2 重叠网格技术

重叠网格法是指将物体的每个部件单独划分网格，然后再嵌入另一套大的网格中，在经过挖洞处理后，非计算域的网格会被排除在计算之外，重叠区域可以通过建立插值关系来传递流场信息。重叠网格技术允许多个相互独立的网格之间产生无拘束的相对运动，因此，其可以很好地处理六自由度的相对运动问题。

本文采用的naoe-FOAM-SJTU求解器是在开源CFD软件OpenFOAM平台的基础上，加入了重叠网格技术和多级物体运动求解模块。在流场求解中，采用Suggar++［23］程序计算得到重叠网格间的插值信息数据DCI（Domain Conectivity Information）。

2 计算模型与网格

本文的计算采用仅带有螺旋桨的KVLCC2船模，船体与螺旋桨的表面模型如图1所示。实船与模型的相关参数如表1所示。

图1 KVLCC2船几何模型Fig.1 The KVLCC2 ship model

表1 模型主要参数Table 1 Main parameters of the ship model

使用重叠网格方法构建船、桨耦合计算模型，以船心为原点划分计算域，其大小分别为-1.5L≤X≤3L，-1.5L≤Y≤1.5L和-L≤Z≤0.5L，其中 L为船长，船艏朝向-X方向。将计算域划分为3个部分，分别为背景网格、船体网格和螺旋桨网格，所有网格均由OpenFOAM自带的网格划分工具snappyHexMesh生成。由于停船操纵时间跨度较长，需要大量的计算资源，故网格数不宜过多，计算采用的背景网格数为57万，船体网格数为268万，螺旋桨网格数为50万。经过Suggar++程序对几套网格进行插值，得到的最终全流场计算网格总数为375万，计算网格如图2所示。

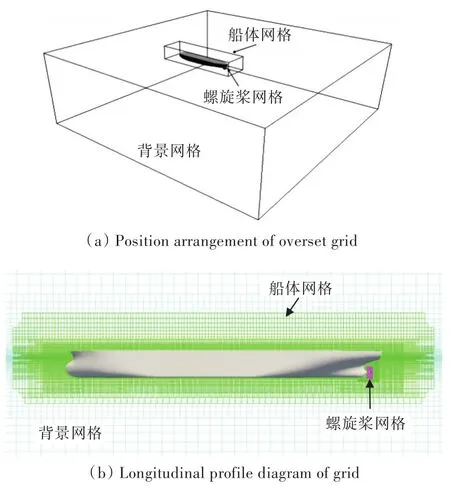
图2 网格布置图Fig.2 Schematic diagram of grid arrangement

3 计算结果与分析

3.1 自航验证

为了验证本文中所使用数值方法的可靠性和所采用网格的收敛性，需要对船模的自航问题进行数值验证。本文采用naoe-FOAM-SJTU求解器，在计算过程中采用PI控制器调整螺旋桨转速，从而使螺旋桨推力与船模所受阻力达到平衡，得到船模的自航点。

根据日本海上技术安全研究所（National Maritime Research Institute，NMRI）试验水池的试验数据，选取该船的设计航速0.76 m/s（对应的实船航速为15.5 kn）进行数值模拟。在该工况下，模型的螺旋桨转速n与船模航速V的时历曲线分别如图3和图4所示。图中：CFD代表预报值，EFD表示试验数据。

图3 船模螺旋桨转速时历曲线Fig.3 Time history curves of propeller revolutions velocity of ship model

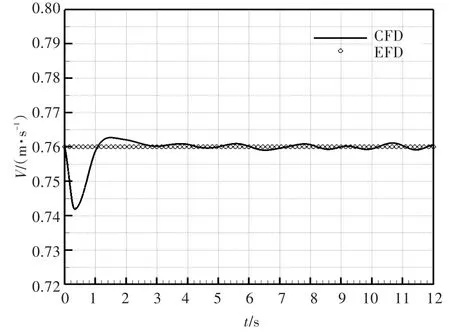
图4 船模航速时历曲线Fig.4 Time history curves of speed of ship model

由图3可以看出，达到预定航速时，预报的螺旋桨转速为 17.02 r/s，与 NMRI水池的试验值［24］17.2 r/s相比仅小了1.05%。可见采用本文所使用的数值计算方法对船模自航进行数值模拟可以较精确地预报出船模的自航点，使用该套网格进行停船操纵的数值模拟较为合适。

3.2 停船操纵数值模拟

本文针对停船操纵的数值模拟过程如下：首先使用PI控制器控制船模以0.490 5 m/s（对应的实船航速为10 kn）的速度航行，在达到稳定自航状态之后，控制螺旋桨倒车进行停船操纵，螺旋桨倒转速度为10.36 r/s。当船模纵向速度降为0时，停船操纵完成。

3.2.1 停船参数预报

停船操纵过程中的船模运动轨迹以及速度随时间的变化曲线如图5所示。

这里使用了无因次化参数，其中图5（a）的轨迹图中使用了无因次化长度，图5（b）的速度变化图中使用了无因次化速度和时间，计算公式分别为：。

图5 船模轨迹与速度图Fig.5 The trajectory and the velocity of the ship model

从图5中可以看出，停船纵距、横距和停船轨迹与试验值吻合较好，其中停船冲程与试验值相比多了0.75%，停船横距与试验值相比少了4.29%，停船时间与试验值吻合较好，而倒车之后的速度变化情况则与试验值存在一定的误差，在余速较高时，采用数值方法预报的速度降低较快。本文采用的数值计算方法可以较为精确地预报船舶停船操纵的相关参数，从而为停船性能评估提供有力的手段。

为了研究倒车停船操纵中船舶停下的力学机理，对船体操纵过程中的受力情况进行了分析，船体受到的总纵向力Ft和该力的分解情况如图6所示。

图6 纵向船体受力Fig.6 The longitudinal force of the ship model

由图6可见，由于螺旋桨处于不停转动的工作状态，故船体受到的总纵向力Ft是波动的，随着船速的减小，该力有逐渐减小的趋势。将总纵向力分解为船体所受阻力Fs和螺旋桨作用力Fp，发现船体阻力曲线比较具有规律性，随着航行时间的增加，船体速度逐渐减小，船体所受阻力也逐渐减小，当航速降为0时，船体阻力也降低为0；而螺旋桨作用力则并无明显的规律性，其在某一数值附近波动是为船模提供刹车力。

3.2.2 停船操纵流场分析

为了分析停船操纵中船舶运动的水动力特征，船模倒车停船操纵进行10 s后（对应的实船为105 s），船艉部的压力分布如图7所示。图中，pd为动压力，表示该处总压力与未经扰动的静水压力之差。

由图7可以看出，在倒车停船操纵过程中，船后方右侧形成了高压区，而左侧因螺旋桨倒车导致压力变化情况较小，相较于右侧可以忽略不计。船后方左、右两侧的压力差形成了推动船艉向左的横向力，从而导致船艏右偏，产生倒车效应。

为了研究船艉右侧高压区产生的原因，对该时刻船艉周围的流场情况进行了研究，船周流体纵向速度Ux和垂向速度Uz的分布如图8～图10所示。

由图8中可以看出，船艉两侧均存在一定大小的伴流，其中右侧高压区附近流体的纵向速度较左侧更大，这是因为在倒转螺旋桨的作用下，其左后方的流体被排向桨的右前方，排出流在向前方运动的过程中受到船体的阻挡，冲击船体右后方而产生压力。

图7 艉部动压分布图Fig.7 The pressure distribution on the aft of the ship

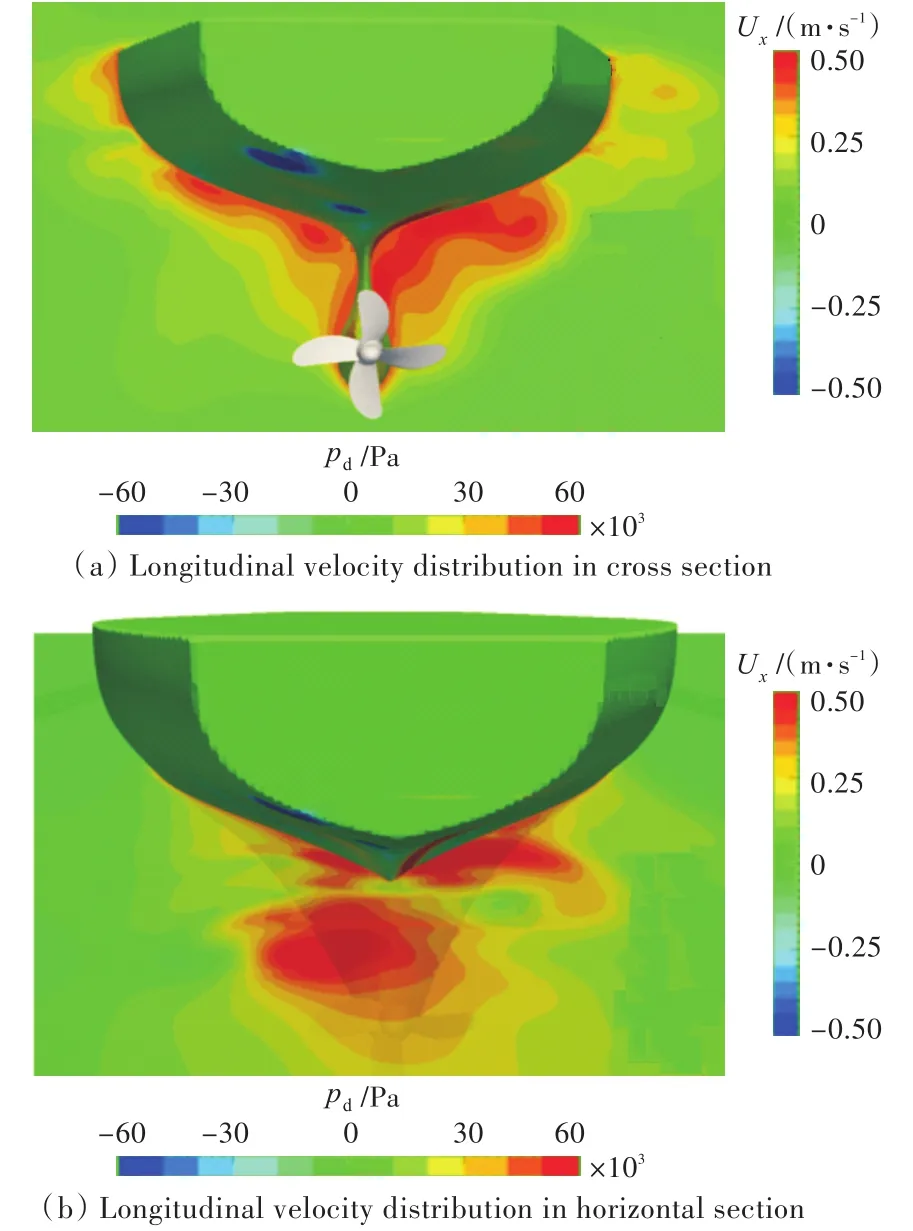
图8 流体纵向速度分布图Fig.8 The speed distribution of X direction

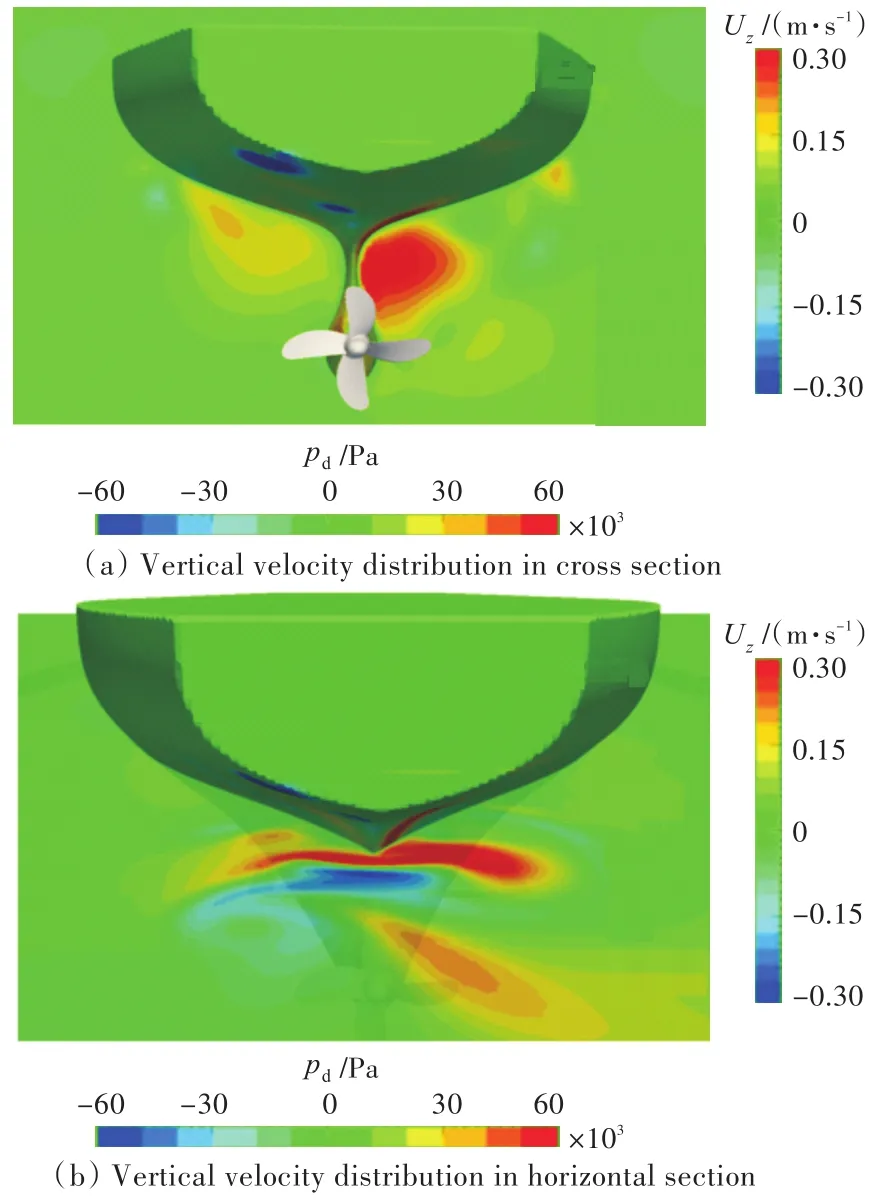
图9 流体垂向速度分布图Fig.9 The speed distribution of Z direction

图10 螺旋桨周围流体速度分布图Fig.10 The speed distribution near the propeller

由图9中可以看出，在倒转螺旋桨的作用下，船艉右侧的流体被向上排出，其在向上运动的过程中受到船体的阻挡，从而冲击船艉右下方，产生一定的压力。而左侧流体则向下运动，流向更深的水域，不对船体表面压力分布产生明显影响。由此，左、右两侧的压力差就形成了推动船艉向左的横向力。

图10清晰地反映出了倒车停船的作用机理：螺旋桨倒车，将流体向前方排出，流体的反作用力作用在螺旋桨上，通过桨轴为船舶提供刹车力。从船艉向船艏看去，倒车螺旋桨逆时针旋转，改变了船艉附近的流体运动情况，右侧排出流在向前方和上方运动时受到船体的阻挡，与船体发生相互作用，在艉部船壳处产生压力，推动船艉向左，从而造成船艏右偏，产生倒车效应。

4 结 语

本文阐述了对停船操纵进行CFD数值模拟的重要意义，介绍了使用基于重叠网格技术的naoe-FOAM-SJTU求解器对倒车停船过程进行数值模拟的方法，结果显示数值预报结果（如停船冲程、停船横距和停船时间等）与试验结果吻合良好，误差在5%以内，表明使用当前数值方法对停船操纵问题进行数值预报是可靠的。

另外，针对船舶从自航到停止的过程，给出了详细的流场信息，如船艉表面压力分布、螺旋桨周围流体速度变化等，分析了产生倒车效应的缘由。本文所采用的求解器可以准确预报出倒车停船操纵下船舶的运动过程和水动力特性，可以为船舶停船性能评估、船舶数字化设计和操纵方式的选择提供可靠参考。

未来，将对浅水情况下的船舶停船操纵进行模拟，并对不同的停船方式进行比较和分析，同时对本文所采用的船舶操纵数值模拟方法进行更为广泛的验证。