小型无人帆船Z形操纵性能预测分析
孙烨,司先才*,2,马靖丰,谭俊哲,2,张雪飞,王树杰,2
1中国海洋大学工程学院,山东青岛266100
2青岛市海洋可再生能源重点实验室,山东青岛266100
0 引 言
在无人帆船实现智能航行的过程中,操纵性对于无人帆船的循迹航行具有一定的影响,是十分重要的航行性能。在船舶操纵性能方面,艉舵发挥着重要作用,包括转弯能力、初始转弯能力、偏航检查能力和航向能力。在设计阶段,船—舵系统的水动力分析对准确预报船体操纵运动具有重要作用。目前,针对船—舵系统操纵性水动力计算的方法主要有经验公式法、系统辨识法、模型试验法和数值计算方法,其中基于CFD数值计算方法预报船舶操纵水动力的研究较多。Liu与Yasukawa等[1-2]基于 CFD 方法,采用 MMG(Ship manoeuvring mathematical model group)方法建立船舶运动数学模型,对船—舵轮廓以及船舶操纵性能和KVLCC2模型船操纵性的影响进行了研究;Sun等[3]采用CFD方法,对Kriso集装箱船的船—桨—舵系统进行了水动力学研究,并对模型和全尺寸KCS船的船—桨—舵系统进行了瞬态两相流计算。Shin等[4]提出了一种用来提高波浪下船舵失速角度的波浪扭曲方向舵,通过CFD方法对其艉舵的水动力性能进行了分析,并将结果与试验结果进行了比较验证。许辉和麻绍钧[5]基于CFD方法计算了不同船速和舵角下的船—舵水动力干扰系数,并与试验结果进行了对比验证分析。冯松波等[6]研究了KVLCC2船在斜航状态下船体与艉舵的水动力学性能,并对CFD方法进行了验证与确认。上述研究大多是针对螺旋桨驱动的船体操纵性水动力进行计算分析,对于以风帆驱动的帆船的操纵性研究较少,并且由于无人帆船结构的特殊性,易受到外界环境的影响而呈现严重的非线性,航向很难控制。因此,准确预报无人帆船船体的操纵性能,对安全航行来说就显得十分重要。
无人帆船船体受风帆的作用,会引起不同的漂角,导致船体产生一定的偏航,此即为船体的斜航状态。在此状态下,操舵可以使船体恢复原有航向,防止船体出现较大的漂角。为了探讨无人帆船的舵力效能对船体操纵性能的影响,本文拟利用Fluent软件建立船体斜航状态下的粘性流场模型。在采用CFD方法模拟船体运动时需要使用动网格技术,会涉及到网格的再生与变形,但当船体的偏航角与运动幅度过大时,网格易出现负体积而导致数值计算发散或是计算结果出现错误。而动态重叠网格技术在处理复杂曲面离散以及物体的大幅度运动方面具有一定优势,处理结构物具有大幅度运动的绕流问题时不需要网格再生,可提高动态网格的处理效率和计算的准确性[7-9]。因此,本文将结合重叠网格技术计算不同漂角与舵角下船体所受到的横向力和转艏力矩、船舵的反偏航力矩与失速角;同时,利用MMG方法将水动力学计算结果代入帆船操纵运动模型中,在Matlab软件中通过编程讨论不同舵角与漂角之间的关系,并利用Simulink模块综合分析船体在迎风状态下进行Z字形航行时的操纵性能。
1 无人帆船模型
1.1 模型参数的选用
本文以自主设计的无人帆船模型为数值模拟研究对象。无人帆船船体(附体)与风帆的主尺度如表1所示,舵剖面选用NACA 0018翼型。

表1 小型无人帆船模型主尺度Table 1 The main dimensions of small saildrone model
1.2 帆—船—舵系统受力分析
坐标系的建立包含大地固定坐标系o0-x0y0z0和载体固定坐标系o-xyz。形成大地表面固定坐标系的x0y0表示船体航行时静止的水面,z0轴垂直向下。载体固定坐标系遵循右手法则,船身轴线为x轴,方向指向船头为正,y轴与船舷垂直,指向船舷右侧为正,z轴垂直于xy组成的平面。船体重心G在载体固定坐标系o-xyz中位于(xG,0,KG-M)点,(x0G,y0G)表示船体重心G在大地固定坐标系中的位置。为简化分析,假设如下:船体与船舵为刚性体,在低航速下不考虑兴波的影响,稳心足够大(横倾角较小),忽略横摇对船体操纵的耦合作用,并且在此阶段只利用xy水平面下船体的三自由度运动模型。图1所示为小型无人帆船船体的受力分析原理图。图中:α为船体运动时的漂角;ψ为帆船航向角;δ为船体舵角;R为船体受水阻力与横向力的合力;Ry,Rx分别为由船体及附体引起的横向力和水阻力;T,N分别为风帆产生的推进力和横向力;P为风帆横向力与推力的合力。由于横倾角的存在,风帆产生的推进力T与水阻力Rx并没有作用在同一作用线上,而是产生了一个偏航力矩MT;此外,风帆气动力的作用点与船体水动力的作用点并不在同一铅垂线上,风帆产生的横向力N与船体以及附体引起的水动力横向力Ry会产生一个反偏航力矩MN[9]。
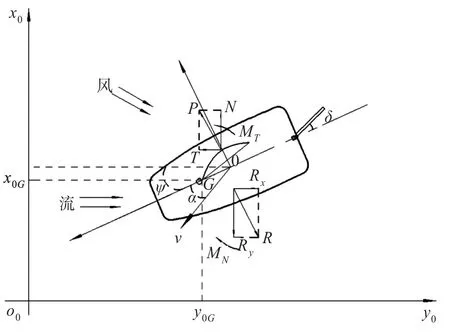
图1 船体受力分析Fig.1 The force analysis of hull
1.3 帆—船—舵运动模型
MMG分离建模方法可将作用于船体的外力以及外力矩分别计算并表示出来,其中包含裸船体、船舵与水流,以及风与帆相互作用的力及力矩,同时考虑船体航向角与舵角之间的关系,结合受力分析,建立无人帆船在静水中的三自由度数学模型为
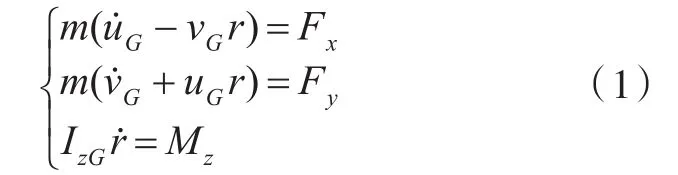
式中:uG,vG分别为重心处船体前进方向速度和横向方向速度,uG=u,vG=v+xGr,其中u为船中心纵荡速度,v为船中心横荡速度,r为舷摇角速度;Fx,Fy,Mz分别为在x,y,z轴附近重心处作用的外力和力矩;m为船舶质量;u̇G,v̇G为对时间的导数;IzG为船舶在重心附近的惯性矩。考虑到船体的附加质量mx,my以及附加惯性矩JzG,式(1)可表示为
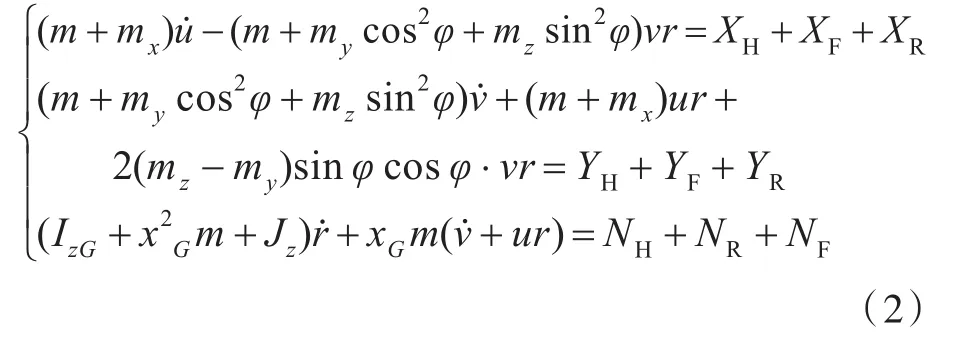
式中:mx,my,mz分别为载体固定坐标系下x,y,z轴的附加质量;Jz为载体固定坐标系下z轴的转动惯量;φ为转艏角度;XH,XF,XR分别为帆船前进方向所受到的来自裸船体、风帆、舵与海风、海流的相互作用力;YH,YF,YR分别为垂直于帆船前进方向所受到的来自裸船体、风帆、舵的力;NH,NF,NR分别为来自裸船体、风帆、舵的舷摇力矩。未知变量u,v,r可通过式(2)求解。式(3)表达的是船舶重心在大地固定坐标系中的位置:

风帆的推进力XF、横向力YF以及舷摇力矩NF可表示为

式中:ρ为空气密度;θ为帆的相对风向角;C1,C2分别为风帆的升力和阻力系数;C3,C4分别为风帆的最大推力系数与横向力系数;C5为转矩系数。结果采用本实验室项目中风帆动力学的计算值。
以下方程为船—舵横向力与力矩计算公式。其中,系数值通过经验公式求解,并与第2节的CFD数值计算结果进行对比分析。

式中:tR为船—舵的减额系数,aH与xH为船—舵的水动力干扰系数;FN为船—舵的正压力;xR为舵中心处纵向坐标。船体非线性流体动力与力矩的理论计算公式[10]为


2 基于CFD方法的操纵水动力求解
进行CFD数值仿真是为对船—舵系统操纵水动力导数的求解与恢复航向效果进行判断,初步确定船—舵的失速角大小以及对船舵的控制参量,以便于后期为船舵的智能控制提供依据。
2.1 计算方法与数值求解
应用Fluent软件进行流场数值模拟,船体周围的三维粘性流场可用雷诺平均的连续性方程和动量守恒方程描述,选用SST k-ω湍流模型结合标准壁面函数模拟边界层中近壁面附近的流场。压力速度耦合采用SIMPLEC算法;压力方程、动量方程和湍流方程均通过二阶迎风格式离散以保证计算精度。对于两相流模拟船体自由面绕流问题,水和空气遵循质量守恒,并利用流体体积(VOF)法处理自由表面;船—舵表面采用无滑移壁面条件。如图2所示,速度入口位于离船艏1.5倍船长处,压力出口距离船艉部3.5倍船长,底部距离船体水线面1.5倍船长,左、右侧壁距离船侧各1.5倍船长。

图2 计算域以及边界条件Fig.2 Computational domain and boundary conditions
2.2 重叠网格技术在三维结构网格中的实现
本文采用重叠网格技术,分别对流场、船体和船舵这3套结构网格进行划分,流体域作为背景网格,船体和船舵作为重叠网格嵌套在背景网格中。在重叠网格技术中,固定的背景网格与嵌套网格结合使用。所谓背景网格,即在流场区域内生成的网格,嵌入背景区域的重叠区域生成的网格为重叠网格。嵌套网格与背景网格重叠,并允许嵌套网格在背景网格内部自由移动和转动。背景与重叠网格之间的信息交换通过传输单元(贡献单元/受体单元),使用线性或距离加权内插算法完成[11-12],并对自由表面处进行单独的网格划分与加密(图3(a)),有效保证计算要求。
2.3 操纵水动力学求解结果
本文以实尺度的船模进行数值模拟,船速U=0.5~1.5 m/s,速度间隔为0.2 m/s,对船体的横向力与转艏力矩进行计算。此外,计算舵角δ的范围为 0°~40°,舵角间隔为 5°;漂角α范围为-20°~20°,间隔为5°。
在CFD计算结果收敛的情况下,计算了船舵的升力系数Cl与阻力系数Cd,进而求得了船—舵失速角(图4)。随后,对不同漂角和舵角下船舶所受横向力与转艏力矩进行求解。为了初步验证本文数值方法的可靠性,将CFD计算值与理论计算值进行了对比(图5),结果显示吻合度较好。另外,还利用最小二乘法对CFD计算结果进行了曲线拟合(图6)。船体的位置导数求解是计算曲线零点斜率,阻力导数求解是通过对船体进行周期性艏摇运动,然后将曲线拟合进行计算求解(图7),表2所示为其计算结果。

图4 不同舵角下舵的升、阻力系数Fig.4 The lift and drag coefficients of the rudder under different rudder angles
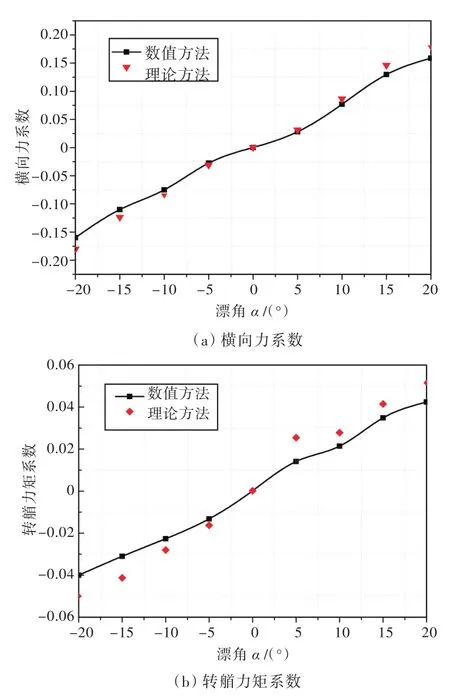
图5 不同漂角下船舶所受横向力系数和转艏力矩系数对比(舵角为0°)Fig.5 Comparison between lateral force coefficients and turning torque coefficients of hull under different drift angles(rudder angle of 0 degree)

图6 最小二乘法拟合结果图Fig.6 Fitting results of least square method

图7 不同风向角下船舵角与斜航角的关系Fig.7 The relationship of the rudder angle and the drift angle under different wind direction angles

表2 船体操纵水动力导数求解结果Table 2 Results of hydrodynamic derivatives of ship maneuvering
如图4所示,当舵角为15°时,舵的升力系数最大,当转到20°状态时,舵的升力系数急剧下降。由CFD计算结果可知,船舵失速角范围为15°~20°。并且,随着舵角的不断增加,舵叶迎流面积增大,舵的阻力系数呈上升趋势。
3 操纵性能分析
根据第1节对帆船受力的分析以及采用三自由度数学模型对帆—船—舵系统进行的分析,讨论舵角与航向角之间的关系;通过对船—舵的水动力学计算结果进行参数拟合,并整合到帆—船—舵系统的MMG模型中(式2),利用Matlab软件中的Simulink模块搭建框图并对帆—船—舵系统的运动进行仿真,分析帆船在不同风向角下船舵的保持航向效能。由图7可知,舵角约在10°之后帆—船—舵系统趋于稳定,船体以较小的漂角(0°~6°)航行,符合帆船正常的航行姿态。
为了量化船舵的舵力航向保持能力,进行了-10°/10°的 Z字形操纵模拟研究[1],绘制的舵角δ和航向角ψ的模拟仿真时历曲线如图8所示。从模拟结果中可以看出,船艏转动随船舵转动的响应程度较快。综上可知,本次船舵的舵效可用于规定工况下船体的航向控制。
4 结 语

图8 航向角随舵角变化的时历曲线Fig.8 The time history curves of the variation of the heading angle with the rudder angle
本文以自主设计的无人帆船的帆—船—舵系统为研究对象,基于Fluent软件,对小尺度模型下无人帆船的水动力进行数值计算,并与理论计算结果进行了对比验证,同时,还将计算结果代入通过受力分析建立的帆—船—舵系统三自由度操纵模型中,对帆船的操纵性进行了预报。研究结果表明,船—舵在不同工况下其水动力性能有所差异,舵力效能将最终影响到船体操纵的机动性。由船—舵的水动力性能与帆船操纵模型可知,基于CFD的方法可以应用到船体水动力计算中,用于预报帆船的操纵性运动,基于CFD的方法还可以应用到帆—船—舵系统在一定漂角、舵角下船体运动的水动力计算中。该研究可为无人帆船在结构设计阶段应用CFD方法预报船舶操纵性打下基础,从而为后期对船舵的智能控制提供依据。未来,可进一步验证船—舵的水动力学计算结果与试验值,分析预报无人帆船在复杂环境下的操纵性。

