多开口甲板板架结构极限承载力实验研究

周红昌 ，孔祥韶*，袁天 ，吴卫国

1武汉理工大学高性能舰船技术教育部重点实验室，湖北武汉430063

2武汉理工大学交通学院，湖北武汉430063

0 引 言

在多开口甲板结构设计中，开口区域的布置形式、尺寸等因素对船体梁极限承载能力的影响一直是设计者关注的问题［1-2］。当船舶甲板或舷侧具有开口结构时，局部典型结构的失稳破坏将对整船极限承载能力产生一定影响。同时，开口区域的布置位置对船体梁的破坏模式也会产生显著影响。因此，研究开口区域的布置形式及其相邻区域甲板结构的失效诱因对于提高船体结构极限承载能力具有重要意义［3］。

加筋板作为最常见的船体结构之一，研究强力甲板处加筋板结构在轴向压缩载荷作用下的极限承载能力至关重要［4］。崔维成等［5］基于大挠度理论，导出了计及初始挠度、焊接残余应力、横向应力和垂向载荷等影响的加筋板格有效带板宽度的理论计算公式。Paik等［6-7］通过采用有限元方法对加筋板在轴向载荷及侧向压力作用下的极限承载力进行研究，分析了初始缺陷、加载方式对其极限承载能力的影响。Xu等［8］采用实验与有限元对比分析的方法，确定了与实测结果相符的初始缺陷系数，发现在相同缺陷幅值情况下，初始挠度的形状对加筋板失稳模式有着重要影响，但对整体极限承载力的影响较小。王东海等［9］结合纵向甲板板格的合成应力和舱口角隅的疲劳强度对甲板大开口结构的强度进行了评估。Yu等［10-11］和Kwon［12］等研究了方形开口的位置、形状及面积等参数对极限强度的影响，归纳出了结构极限强度的折减参数计算公式。

上述文献的研究对象均为连续加筋板或甲板仅存在单一开口的模型，尚未探讨多开口及开口位置的布置形式对甲板整体结构轴向受压稳定性的影响规律。鉴于此，本文将在设计制作的甲板及舷侧开口板架模型和双开口甲板板架结构模型的基础上，观测2种模型在轴向压缩载荷作用下失稳破坏的完整过程，详细阐述应力的变化特点，对比分析开口位置对整体结构的屈曲失效模式和极限承载能力的影响。

1 模型方案设计

1.1 多开口板架结构模型设计

为了研究多开口布置形式对甲板板架结构极限承载能力的影响，以甲板及舷侧结构为考察目标，分别设计了不同开口形式的甲板板架结构模型（模型1和模型2）。图1和图2所示模型1分别为甲板及舷侧开口板架结构；图3所示模型2为甲板具有2个开口且尺寸不同的板架结构，其中舷侧结构为连续板材。以上图中，数值单位均为mm。多开口板架结构模型的材料均为Q345B钢。表1给出了模型各构件的尺寸。

图1 模型1甲板结构图Fig.1 Deck structure diagram of model 1

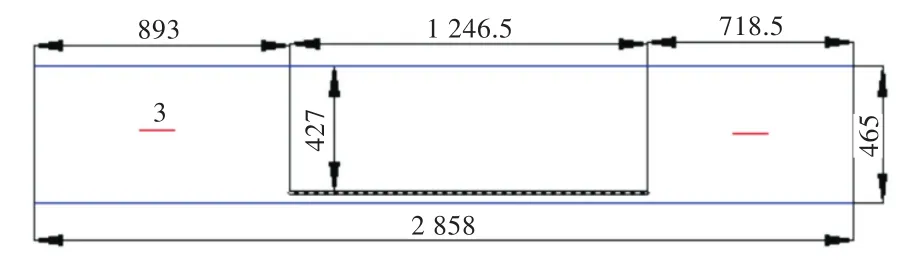
图2 模型1舷侧结构图Fig.2 Broadside structure diagram of model 1

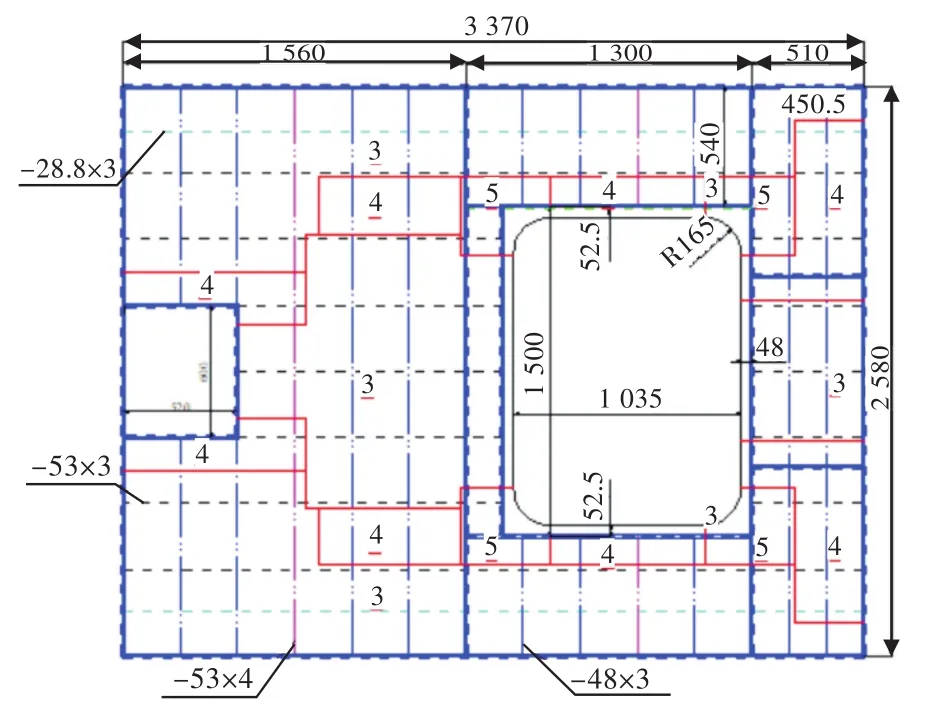
图3 模型2甲板结构图Fig.3 Deck structure diagram of model 2

表1 多开口板架结构主要构件尺寸Table 1 The main dimensions of deck grillage structure with multiple openings

1.2 实验工装及应力测点布置

1.2.1 边界条件

模型1与模型2在固定端均采用固支边界条件，加载端采用简支边界条件［12］。为实现固支和简支边界条件，设计了加载端和固定端的约束工装。在模型舷顶列板两侧焊接了一定长度的圆钢，并镶套在与地面固定连接的钢制滑道内，使模型在长度方向可自由滑动，而沿高度方向无法运动，以此满足加载端简支边界条件的要求，如图4（a）所示。固定端的实验工装一端与甲板板架结构模型焊接，另一端与门架栓接，以此满足固支条件的要求，如图4（b）所示。

图4 模型的边界条件Fig.4 The boundary conditions of the model

1.2.2 加载方案及设备布置

按照上述约束工装的连接方式，将模型固定在门架之间。加载端通过采用6台水平固定在门架与模型之间的液压千斤顶进行轴向压缩载荷的施加。6台千斤顶由同一液压油泵提供顶升压力，在液压千斤顶端头与模型之间固定有一套压力传感器，以实时记录轴向压缩载荷值。在模型两端均匀布置有3对百分表位移计，取两端百分表位移计数据差值的平均值作为模型轴向压缩的位移。2种甲板板架结构模型采用相同的加载方案，图5所示为加载实验示意图。表2给出了2种甲板板架结构模型进行轴向压缩实验时采用的相关仪器及设备。

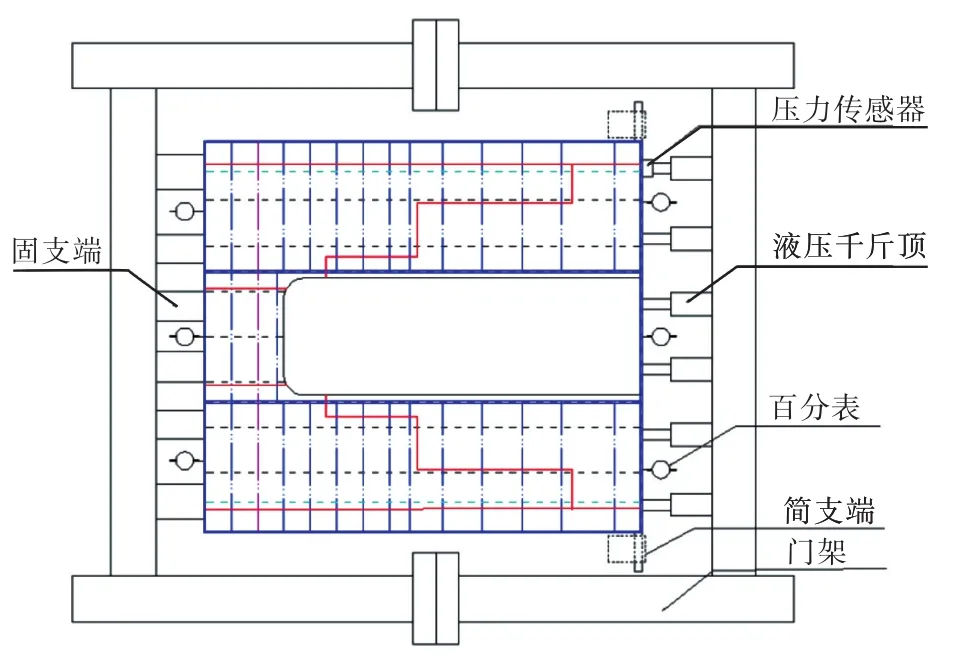
图5 模型加载实验示意图Fig.5 Schematic diagram of loading in the model experiment

表2 实验采用的相关仪器设备Table 2 Related instruments and equipments in the experiment

1.2.3 应力测点的布置方案

在2种板架结构（模型1和模型2）的甲板上布置有一定数量的应变片，用于记录实验中多开口板架结构的甲板应力变化情况。

为进行对比验证，如图6所示，在模型1的甲板板架结构左侧布置了40个应变测点（A1～A40）。因该板架结构为对称结构，故右侧布置的测点数目相应减少，实际只布置了30个应变测点（B1～B30）。甲板开口区域为主要关注对象，在加载过程中，因其主应力方向无法精准确定，故均采用三相应变片进行监测，其他区域则沿甲板长度方向布置单相应变片。

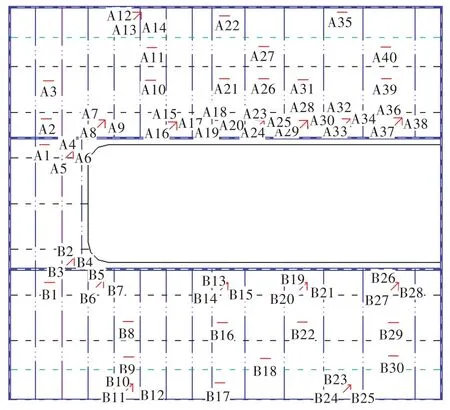
图6 模型1的测点布置图Fig.6 Layout of the measuring points on model 1

同理，根据相同的测点布置原则，在模型2的甲板板架结构上布置了相应数量的应力测点，如图7所示。

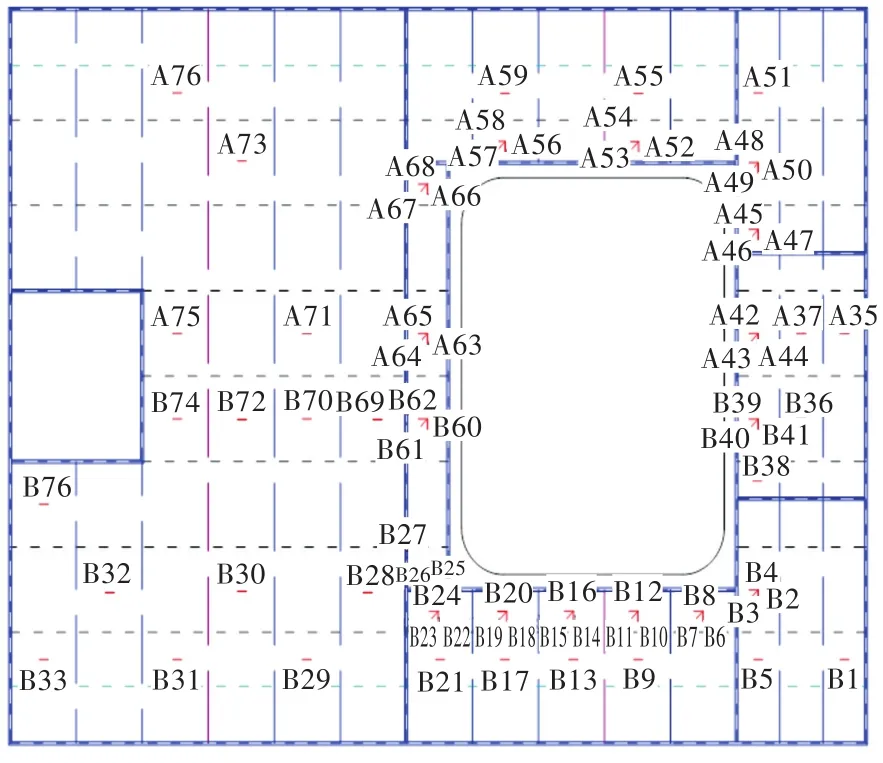
图7 模型2的甲板测点布置图Fig.7 Layout of the measuring points on model 2

2 模型实验

2.1 加载过程

为了检查数据采集系统的有效性并释放焊接残余应力，在极限破坏实验前先进行了3次小载荷加载［13］。根据数据采集系统监测到的各测点的应变情况，将测量失效的应变片进行替换，以保证测量系统的准确性。加载时，按60 kN的载荷增量步逐级加载，表3给出了3次预加载的最终载荷数值。在进行破坏实验时，载荷增量步减小，调整为20 kN，直至结构发生失稳破坏为止。

表3 预加载最终载荷值Table 3 Final load values of preloading

2.2 结果分析

2.2.1 破坏模式对比分析

1）模型1。

在进行加载实验时，当轴向压缩载荷增加至888 kN时，随着载荷的进一步增加，模型1开口区域中部发生了明显的屈曲现象。压力传感器的检测数据显示，此时板架结构的承载能力明显下降，说明此时结构已发生失稳破坏。图8所示为模型1在轴向载荷作用下发生失稳破坏后甲板及舷侧结构大开口区域的破坏模式。在实验过程中，模型1右边舷侧结构大开口处的甲板首先发生明显的下扰（凹陷）现象，且下扰幅值不断增大。随着轴向载荷的增大，模型1开口区域右侧甲板结构与纵舱壁连接处出现了明显的褶皱现象，整体板架最后的破坏模式表现为右侧甲板失稳破坏。

图8 模型1的屈曲破坏模式Fig.8 Buckling damage mode of model 1

2）模型2。

在进行加载实验时，当轴向压缩载荷达到1 134.6 kN并持续增大时，模型2甲板开口两侧同时出现了明显的褶皱现象。模型2的破坏区域与模型1的类似，均在甲板开口中部发生崩溃，且失稳破坏模式也基本相同。但模型2在破坏前的加载过程中，相较于有舷侧开口的模型1，甲板变形不明显，其失稳破坏过程具有一定的突发性。

图9 模型2的屈曲破坏模式Fig.9 Buckling damage mode of model 2

2.2.2 甲板应力变化特点

1）模型1。

图10和图11所示为模型1甲板左、右两侧的应力变化情况。

由图10可知，在加载的初始过程中，结构处于弹性变形阶段，当压缩载荷超过58 tf后，各测点的应力急剧增大，此时结构进入弹塑性变形阶段。其中，三相应变片A23～A25及A32～A34对应的开口右侧甲板中部与舷侧交接处发生了褶皱现象，应力增长速率明显高于其他区域。当结构发生失稳破坏时，右侧甲板出现了大面积的凹陷，而单相应变片A27、三相应变片A12～A14对应的甲板凹陷区域和舷侧开口两端对应的甲板区域，此时应力幅值陡增。

由图11可知，模型1左侧甲板应力变化较为平缓，当轴向压缩载荷达到65 tf后才开始进入弹塑性变形阶段。虽然开口左侧甲板的变形没有右侧甲板的明显，但其对应区域测点应变片B19～B21和B26～B28的应力也明显高于其他区域。对比模型1开口左、右两侧相同区域测点的应力变化情况可以发现，在弹性变形范围内两侧甲板的应力情况基本相同。当模型1进入弹塑性变形阶段后，开口右侧的甲板与舷侧相邻区域的应力增量明显大于左侧，其他区域则无明显差别。

2）模型2。

图12和图13所示为模型2甲板左、右两侧的应力变化情况。相较于甲板及舷侧同时具有开口的板架结构（模型1）而言，甲板双开口板架结构（模型2）的弹性变形范围更大，当进入弹塑性变形阶段后，结构迅速发生失稳破坏。

由图12和图13可知，模型2甲板右侧在加载载荷达到107 tf前主要发生的是弹性变形，当轴向压缩载荷达到107 tf后，板架结构应力集中区域开始发生塑性变形并失稳。三相应变片B18～B20及A56～A58所在测点区域在弹性变形阶段结束后，结构发生塑性变形，产生了明显的褶皱现象。在加载过程中，该区域的应力始终大于其他区域。随着加载的轴向载荷逐渐增大，该处的结构较其他区域的结构先发生失稳破坏。如图13所示，三相应变片B22～B24及B25～B27虽设置在开口角隅附近，但测量得到的应力幅值仍然较小。

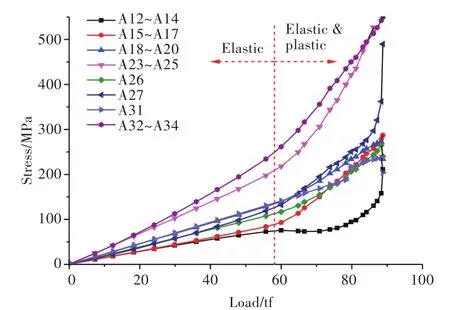
图10 模型1甲板右侧典型测点处载荷—应力曲线Fig.10 Load-stress curves of typical measuring points on the right deck of model 1

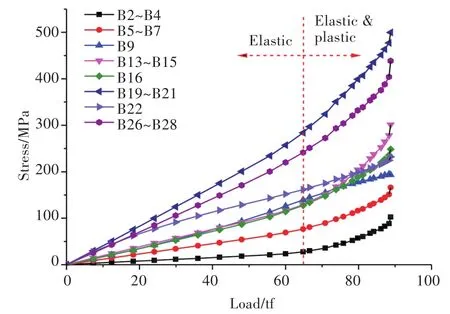
图11 模型1甲板左侧典型测点处载荷—应力曲线Fig.11 Load-stress curves of typical measuring points on the left deck of model 1

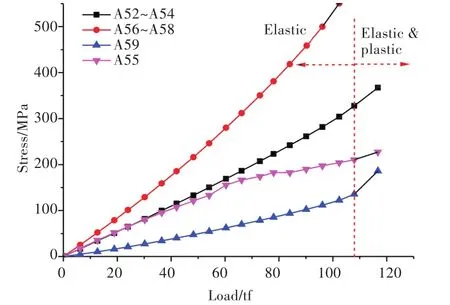
图12 模型2甲板右侧典型测点处载荷—应力曲线Fig.12 Load-stress curves of typical measuring points on the right deck of model 2

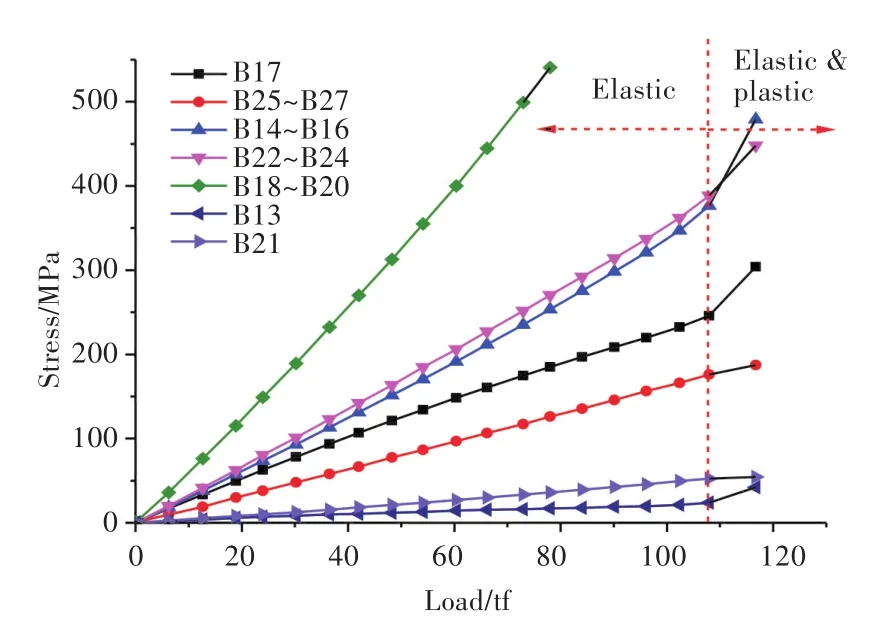
图13 模型2甲板左侧典型测点处载荷—应力曲线Fig.13 Load-stress curves of typical measuring points on the left deck of model 2

2.2.3 极限承载力对比

图14所示为模型1和模型2的载荷—位移曲线。对比2种模型在加载初始阶段的载荷—位移曲线斜率及发生失稳破坏时的极限承载能力F′max（模型1）、F″max（模型2），发现有如下特点：

1）模型1的初始轴向刚度大于模型2的初始轴向刚度，原因是模型2的甲板开口宽度大于模型1的甲板开口宽度，其承受载荷的横截面积较小，轴向抗压缩变形的能力较弱；当轴向压缩载荷超过A点后，模型1舷侧开口对应的甲板下扰（凹陷）明显，轴向刚度明显减弱，但仍具有一定的承载能力；当轴向载荷达到888 kN后，模型1的结构发生失稳破坏。

图14 载荷—位移曲线Fig.14 Load-displacement curves

2）模型2仅在甲板上存在开口，其他区域的结构连续性较好，弹性变形阶段维持较久。当轴向压缩载荷超过B点后，甲板局部发生屈曲变形。随着压缩载荷进一步增大，达到1 134.60 kN时，模型2的结构发生失稳破坏。

表4给出了模型1和模型2在轴向压缩载荷作用下结构极限承载能力与压缩位移的对比结果。

表4 失稳破坏数据对比Table 4 Data comparisons of buckling failure

3 结 论

本文以多开口甲板板架结构为研究对象，开展了甲板及舷侧均含开口的板架结构模型（模型1）和甲板含双开口的板架结构模型（模型2）在轴向压缩载荷作用下的极限承载力实验研究，通过观测和实验数据分析，得到如下结论：

1）在轴向压缩载荷作用下，舷侧开口模型较甲板开口模型更早发生屈曲，且舷侧开口板架模型的极限承载能力明显低于甲板开口模型。

2）在轴向压缩载荷作用下，小开口对结构整体极限承载力的影响不大，甲板板架多开口结构最终的失稳破坏区域均在最大开口处，且集中在中部区域。

3）甲板开口尺寸对结构初始轴向刚度的影响较大，舷侧开口结构在弹塑性变形阶段对极限承载力的影响占主导地位。