基于一方程转捩模型的狭缝冲击射流传热数值模拟

黄华坤 ，张桂勇*，2，3，孙铁志 ，宗智 ，2，3

1大连理工大学船舶工程学院辽宁省深海浮动结构工程实验室，辽宁大连 116024

2大连理工大学工业装备结构分析国家重点实验室，辽宁大连 116024

3高新船舶与深海开发装备协同创新中心，上海200240

0 引 言

冲击射流现象是指具有一定速度的流体通过撞击物体表面，使得撞击区形成极薄的边界层，从而得到较高传热效率的现象。冲击射流传热原理被广泛应用于工业生产，如纸张干燥和电子元器件冷却等。在船舶领域，船舶甲板上的武器发射、无人机发射和垂直起降飞机起飞过程中产生的高温高速喷射气流，不仅会引起甲板的烧蚀，而且还会带来残余热应力的影响。因此，准确预测冲击射流的物理现象，对其工业应用具有重要意义。

许多学者对冲击射流现象开展了研究。Gardon等［1］通过实验发现，在较低冲击距离下，以局部努塞尔数（Nu）表示的传热率表现出第2峰值的特征；当冲击距离较大时，局部努塞尔数的第2峰值消失。Colucci等［2］研究了低冲击距离下（H/D ＜2，H/D为圆形冲击射流的冲击距离，H为冲击高度，D为喷嘴直径）的冲击射流现象，指出局部努塞尔数第1峰值主要受边界层厚度的影响，第2峰值主要受层流到湍流转捩的影响。随着计算流体力学（CFD）和计算机技术的发展，CFD方法被广泛用于模拟冲击射流现象。在早期的数值研究中发现，两方程湍流模型在滞止点处易产生较高的湍动能 k［3-4］，为此，Kato-Launder模型被用于降低滞止点处的湍动能［5］。此外，针对局部努塞尔数第2峰值的特征，研究表明，SST k-ω模型表现较好［6］。然而，Dutta等［7］指出，基于SST k-ω的低雷诺数模型虽然在低冲击距离下（H/B=4，H/B为狭缝冲击射流的冲击距离，B为喷嘴宽度）获得了第2峰值的特征，但在冲击距离变大时（H/B=9.2），该模型预测出了实际不存在的第2峰值。为正确反映冲击射流在不同高度下的特点，Alimohammadi等［8］研究了基于转捩理论的四方程γ-θ模型（也称Transition SST模型）在圆形冲击射流中的表现。结果表明，γ-θ模型可准确预测圆形冲击射流的传热特征；针对不同的冲击高度，γ-θ模型表现出较好的预测能力。但在圆形冲击射流中表现良好的湍流模型在狭缝冲击射流中可能获得较差的结果，反之亦然［9］。同时，γ-θ模型不能预测滞止区附近低湍流强度（Tu＜0.5%）下的横流失稳现象。

因此，本文拟引入基于γ-θ模型的一方程转捩模型来模拟狭缝冲击射流现象。该模型耦合了横流转捩模型，在模拟横流失稳现象和分离流问题上具有一定的优势。同时，将一方程转捩模型与Kato-Launder模型和SST k-ω模型耦合，并在此基础上研究一方程转捩模型在预测狭缝冲击射流传热规律上的表现。

1 数值计算方法

1.1 控制方程

不可压缩湍流流动的时均Navier-Stokes方程的质量守恒方程、动量方程和能量方程分别为：

式中：ρ为密度；μ为动力粘性；u和u′分别为平均速度和脉动速度；p为压力；Cp为比热容；K为传热率；T和T′分别为平均温度和脉动温度；分别为雷诺应力张量和湍流热通量矢量；i和j分别为x，y方向。

1.2 SST k-ω湍流模型

本文采用Menter［10］提出的一种混合标准k-ε模型和k-ω模型的SSTk-ω模型。该模型的湍流粘性系数μt定义为

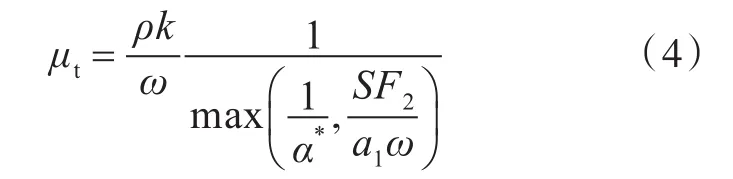
式中：k为湍动能；ω为比耗散率；α*为阻尼因子；a1=0.31；S为应变率；，y为到壁面的距离。

为了封闭控制方程，在模型中增加了湍动能k和比耗散率ω方程，表达式为：

式中，Gk为湍动能k的产生项；Gω为比耗散率ω的产生项；Yk，Yω分别为k和ω的耗散；Dω为交叉扩散项；Sk，Sω分别为k和ω的源项；σk和σω通过混合函数F1进行定义，具体为

式中，下标1，2分别为k-ω模型和k-ε模型的湍流常数。

1.3 Kato-Launder模型

Kato-Launder模型修正在Gk中采用涡量代替某个应变率，能避免两方程模型在滞止点处预测的湍动能k过高的问题。由于在滞止点附近的流动几乎呈无旋状态，涡量趋于0，因此湍动能k变小。该方程的湍动能产生项为

Kato和Launder修正后的表达式为

1.4 一方程转捩模型

在γ-θ模型中引入了转捩临界动量厚度雷诺数和间歇因子输运方程。基于γ-θ模型的一方程转捩模型保留了间歇因子输运方程，同时使用经验关系式取代了临界动量厚度雷诺数方程。其中间歇因子γ的输运方程为

式中：σγ=1.0；Pγ和Eγ的定义为

式中：Flength为控制转捩区的长度；ca2=0.03，ce2=50；Fonset和Fturb的定义为

1.5 计算模型及求解设置

计算模型如图1所示，L为冲击板长度。由于计算模型关于y轴对称，为提高计算效率，建立1/2模型进行计算。表1给出了计算模型尺度和网格节点分布情况。

图1 冲击射流的计算模型Fig.1 The computational model for jet impingement flow

本次计算基于Fluent软件，使用有限体积法对计算域进行离散，选择压力基稳态求解器和压力耦合方程半隐式（SIMPLE）算法。梯度离散格式采用最小二乘法，压力离散格式采用交错压力格式（Pressure Staggering Option），其他离散格式采用二阶迎风格式。湍流模型采用SST k-ω模型、Kato-Launder模型和转捩模型（以下简称为“一方程转捩模型”）。网格划分方案如图1所示。本文采用结构型网格，根据 Jaramillo［12］的研究，保持第1层网格节点与壁面间的无量纲距离y+＜2.5（，其中τw为壁面处的切应力），如图2所示。在壁面和射流出口附近进行网格加密，加密方向如图1箭头方向所示，以渐疏式网格扩展到整个计算域，同时保证网格膨胀率小于2。表1给出了计算模型尺度以及进行网格无关性检验后在x轴和y轴方向的节点分布情况。

2 结果分析与讨论

2.1 稳态冲击射流验证

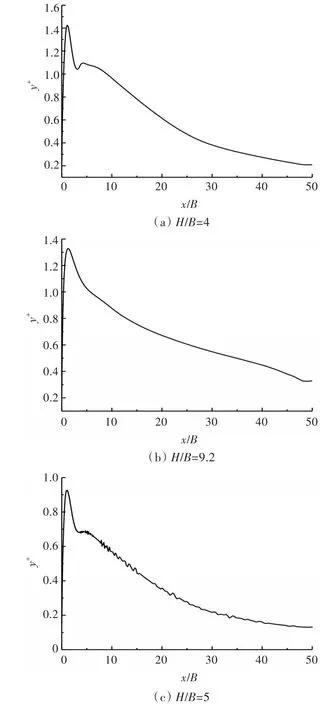
图2 3种算例下 y+沿冲击板的分布Fig.2 y+distributions along the impinging plate for 3 cases

表1 计算模型的尺度和网格节点分布Table 1 Scale and nodes distribution of computationalmodel

为了验证一方程转捩模型对稳态冲击射流换热的有效性，本文采用了 Ashforth-Frost等［13］的实验工况，并与其他学者的数值计算结果进行了对比。实验研究结果表明，在H/B=4时，局部努塞尔数表现出明显的第2峰值特征；而在H/B=9.2时，局部努塞尔数的第2峰值消失。这2个算例可以验证一方程转捩模型对转捩的预测能力。Ashforth-Frost等［13］的实验是在1个标准大气压下进行的。射流出口温度为恒温300 K，射流出口平均速度雷诺数基于射流出口宽度，其大小为20 000。冲击板设为恒温310 K，无滑移固定壁面。上限板设为恒温300 K，无滑移固定壁面。出口采用出流（outflow）边界条件，出口压力为1个大气压P=101 325 Pa。计算的普朗特数Pr=0.72。

图3给出了H/B=4时，得到的局部努塞尔数与实验数据以及其他学者的数值结果沿冲击面的分布情况。从图中可以看出，一方程转捩模型可准确预测局部努塞尔数第1峰值和第2峰值的大小及位置。受转捩过程影响，在3≤x/B≤7范围内，传热率逐渐升高；当转捩完成后，传热率逐渐降低。在滞止点附近，流动处于低湍流强度状态，即准层流状态，这使得滞止点附近相对于壁面射流区的传热率得到了极的大提高。

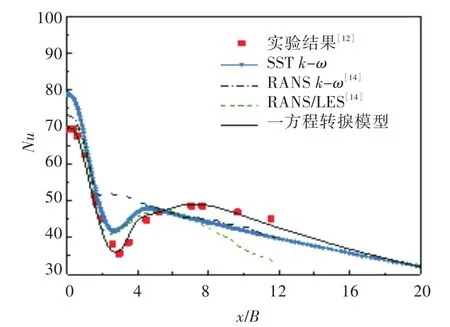
图3 H/B=4时局部努塞尔数分布Fig.3 The distribution of local Nusselt number（H/B=4）

受益于Kato-Launder模型修正作用，可用一方程转捩模型准确预测局部努塞尔数的第1峰值。如前所述，在滞止点处，流动几乎处于无旋状态，因此Kato-Launder模型中涡量的引入使滞止点处的湍动能下降；且在第2峰值附近可明显看到涡的存在（图4）。虽然Kato-Launder模型无法对涡进行计算，但是涡的脱落导致涡量增加，故一方程转捩模型在2次峰值附近预测的传热率与SST k-ω模型相比有所增加，从而提高了涡附近湍动能的预测精度［14］。而无修正模型的RANS k-ω模型［15］和 SST k-ω模型在滞止点处过高地预测了局部努塞尔数。其中RANS k-ω模型无法预测局部努塞尔数的第2峰值。SST k-ω模型虽然能够预测第2峰值，但其预测结果低于实验值，且第2峰值的位置与实验值相比提前了31%，这也说明转捩模型的加入使一方程转捩模型具备了良好的转捩预测能力。因粘性底层的流动状态与湍流转捩相关，故没有粘性底层修正的SST k-ω模型和RANS k-ω模型难以准确预测转捩区间的位置。RANS/LES模型［15］继承了大涡模拟（LES）模型在滞止点附近湍流强度几乎为零的特点，因此正确地捕捉到了局部努塞尔数的第1峰值，但却提前预测了第2峰值的位置。除一方程转捩模型外，其他数值模型同样存在第2峰值预测不准确的现象。整体上，一方程转捩模型获得了与实验结果基本一致的分布趋势，这说明该模型不仅能准确模拟滞止点附近的流动状态，还能准确预测壁面射流区层流到湍流的转捩过程。

图4 H/B=4时的流线图Fig.4 The streamlines for H/B=4

图5给出了H/B=9.2时的数值计算与实验结果中局部努塞尔数沿冲击面分布的对比结果。从图可看出，局部努塞尔数的第2峰值消失。图6显示了H/B=9.2时的流线图，可见回流中心位置较H/B=4时的远，因此在0≤x/B≤10范围内受涡的影响较小。由于转捩受涡的影响，其对传热的影响变弱，局部努塞尔数的第2峰值消失。RANS/LES模型和一方程转捩模型的预测结果与实验结果吻合较好。此外，RANS k-ω模型［15］在滞止点附近预测的局部努塞尔数与实验值相比更低。这是因为在较大的冲击距离下，模型中的应力限制器对流动几乎无影响，这导致滞止点附近的湍流强度升高，传热率下降。而RANS/LES模型［15］则稍好于RANS k-ω模型［14］，但误差仍然有12%。一方程转捩模型较为准确地预测了滞止点处的局部努塞尔数。RANS k-ω模型［14］预测的局部努塞尔数第2峰值与实验值不相符，而RANS/LES模型和一方程转捩模型在趋势上则与实验结果基本保持一致。与一方程转捩模型相比，SST k-ω模型在滞止点处过高地预测了局部努塞尔数，这反映出Kato-Launder模型起到了降低滞止点处湍动能的作用。但在下游区域，SST k-ω模型与一方程转捩模型预测的局部努塞尔数基本一致，这说明在高冲击射流情况下，转捩模型对传热预测的影响较小，同时表明一方程转捩模型可正确反映冲击射流中的转捩强度，从而准确给出局部努塞尔数的分布。

图5 H/B=9.2时局部努塞尔数分布Fig.5 The distribution of local Nusselt number（H/B=9.2）

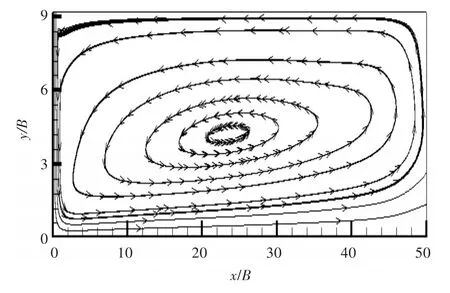
图6 H/B=9.2时的流线图Fig.6 The streamlines for H/B=9.2

2.2 脉动冲击射流验证

脉动冲击射流与稳态冲击射流的不同之处在于，其提供了一个扰动源。Lytle等［16］的研究表明，平行于冲击面的速度脉动峰值与冲击面的平均传热率峰值相关，而扰动源又与涡的形成相关。涡影响了射流的发展以及层流到湍流的转捩过程，进而影响到冲击面上的传热分布。在此，我们采用了Mladin等［17］的实验工况。在本算例中，射流出口采用正弦变化的速度分布，其公式为

式中：vavg为入口的平均速度；A为脉动幅度；fr为脉动频率；t为时间。射流进口温度为300 K。冲击板是厚度为5 mm的铝镍材质，导热率为150 W·m-1·K-1，温度设为 323 K，无滑移固定壁面；上限板的温度设为恒温300 K，无滑移固定壁面。出口设置为出流边界条件，出口压力为1个大气压P=101 325 Pa。计算得到的冲击高度为H/B=5，普朗特数Pr=0.72。

图7给出了在稳定状态下局部努塞尔数沿冲击面的分布情况。从图中可以看出，局部努塞尔数的第2峰值仍然较为明显。这是因为回流中心在x/B=10.8处，如图8所示。一方程转捩模型能准确捕捉到滞止点处局部努塞尔数的大小，同时也能准确预测局部努塞尔数第1个最低点的值。而k-ω-v2-f（k-ω模型和v2-f模型）混合模型［18］则过低地预测了滞止点和最低点处的局部努塞尔数；在下游区，k-ω-v2-f模型［18］的表现较一方程转捩模型差。一方程转捩模型获得了与实验基本一致的结果。这是因为一方程转捩模型引入了间歇因子输运方程来模拟转捩，而转捩的发生与扰动相关，因此对于脉动冲击射流，一方程转捩模型依然能够给出较为准确的结果。

3 结 语

本文提出采用一方程转捩模型对狭缝冲击射流问题进行数值模拟，并研究不同冲击高度、不同雷诺数下的稳态冲击射流和脉动冲击射流传热分布规律。结果表明，一方程转捩模型不仅能捕捉到局部努塞尔数的第1峰值，也能准确预测受转捩影响的局部努塞尔数第2峰值的大小和位置。在4≤H/B≤9.2时，一方程转捩模型在传热预测上表现出了良好的鲁棒性特征。