基于弯矩影响系数的轴系安装状态评估逆计算方法
陈昊,周瑞平*,雷俊松,张建军
1武汉理工大学能源与动力工程学院,湖北武汉430063
2中国船级社上海规范研究所,上海200135
0 引 言
船舶推进轴系安装状态的好坏直接影响到轴系长期运行的可靠性,必须在其安装完成后进行检验,确定轴系的状态。应变检测是一种精度高且适用性强的检测方法,已成为船舶轴系安装检测的主要方法之一。针对船舶推进的应变测试技术发展至今已有30余年,其测试方法和分析模型也有很多种。Cowper等[1]利用应变测量和力矩平衡原理,在集装箱船和车辆滚装船上进行了实船测试及轴承负荷分析。汪骥等[2]研究了基于应变波形和力矩平衡原理的轴承负荷检测方法,这两者都是以力矩平衡原理直接计算出艉轴承和中间轴承的轴承负荷,无法计算主机负荷和其他状态参数。Zhang等[3]提出了一种结合传递矩阵法和应变检测对涡轮机组轴系状态进行分析的方法,其测量对象为涡轮机组,相对船舶推进轴系其测点布置限制较少。美国船级社(ABS)[4]结合应变测量与遗传算法开发了轴承变位测量软件,并将其应用于船体变形研究。日本船级社(NK)[5]在其轴系校中指南中介绍了弯矩影响数以及如何将其用于轴承变位求解的方法,但没有对不同类型轴系的测点布置规律和布点优化进行系统研究。
目前,轴系校中计算的理论方法主要有传递矩阵法、三弯矩法和有限元法。其中,传递矩阵法在截面数过多时易产生较大的累积误差;三弯矩法计算精度较高,相比有限元法具有编程容易的特点[6]。三弯矩法虽然求解计算量大,但其将轴系整体受力情况归纳到了一个矩阵方程中,便于分析轴系各部分之间的相互影响。
本文将从三弯矩方程入手,推导弯矩影响系数,借助轴系任意截面弯矩与轴承变位的线性关系,列线性方程来推算轴系状态。首先,对弯矩影响系数的特性进行研究,推导不同轴系以直接求解最大轴承数,并在此基础上得出适用于不同轴系类型的测点布置规律。然后,对不同测点布置下求解矩阵的条件数进行分析,得出测点优化布置的原则。最后,根据38 500 DWT散货船实轴测试数据推算其轴系状态,验证计算方法的正确性,为轴系应变测试提供一种新的思路。
1 弯矩影响系数法
1.1 弯矩影响系数的推导
对于具有n个截面的变截面梁轴系模型,一共可以列出n-2个三弯矩方程[7]:

式中,li为轴系各单元的长度;EiIi为弯曲刚度;qi为均布载荷;Mi为各截面的弯矩;zi为各截面的挠度。再加上首、尾截面2个边界条件方程以及n个虚支承处支反力为0或实支承处挠度为轴承变位的补充方程,共计2n个方程,可以解出n个截面弯矩和n个截面挠度,将其表示成矩阵形式:
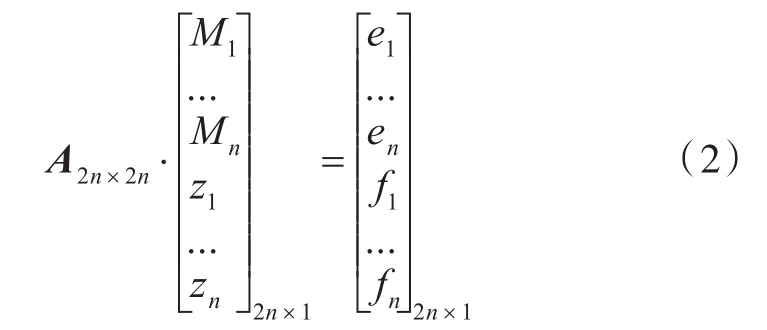
式中,A为2n×2n的系数矩阵;向量C=[e1…en f1…fn]T中各项由方程右侧常数确定,对于建立完成的模型,这两者是定常的;向量X=[M1…Mnz1…zn]T为一个2n行的列向量,表示所要求解的弯矩与挠度。式(2)又可以表示为A-1·C=X,包含2n个方程,前n个用于求解弯矩的方程可以表示为

式中:xi为第i个轴承的变位;ci为直线状态下该截面处的弯矩值;ain为第n个轴承单位变位对第i个截面所造成的弯矩变化量,即弯矩影响系数,kN。对于含有n个轴承和m个截面的轴系来说,其弯矩影响系数可以组成一个m×n的矩阵,每一列都为一个轴承对所有截面的弯矩影响系数。
1.2 基于弯矩影响系数的轴系状态逆计算方法
在推导出弯矩影响系数后,利用轴承变位与截面弯矩之间的线性关系,列出线性方程可以求解轴承变位,进而得出轴系整体状态:

式中,xn为第n个轴承的实际变位;为第n个轴承的实际弯矩;Mn0为第n个轴承在直线状态下的弯矩。理想情况下,若要求得n个轴承的变位,只需测得n个截面处的弯矩即可。需要注意的是,为得出正确的计算结果,必须尽可能正确简化模型来得到正确的直线弯矩值。
2 测点布置规律与优化原则
2.1 弯矩影响系数性质
研究发现,式(4)中的系数矩阵是不满秩的,原因是矩阵各行线性相关,造成矩阵奇异。要找出矩阵奇异的原因,必须对弯矩影响系数的性质进行研究。图1为4#轴承弯矩影响系数在轴线方向上的分布。

图1 轴承弯矩影响系数分布图Fig.1 Distribution of bending moment influence coefficient on shaft
从图1可以看出:每个轴承的弯矩影响系数在轴线长度方向上都为连续直线,且在每一跨梁内斜率、截距均各不相同;越靠近轴承的截面其弯矩影响系数越大,越远离轴承的截面其弯矩影响系数越小;从船艉向船艏看,在第1个轴承前(包括第1个轴承处)及最后一个轴承后(包括最后一个轴承处),弯矩影响系数均为0。
对含有n个轴承的轴系,由于弯矩影响系数与截面位置成线性关系,第1跨梁和第n-1跨梁内独立弯矩数最大为1,第2至第n-1跨梁内独立弯矩数最大为2,当跨梁内待测弯矩数大于最大独立弯矩数时,可以依据线性关系确定跨梁中所有截面的弯矩。前一跨梁内所有截面弯矩确定后,后一跨梁会减少1个独立弯矩数。
将1~n-1跨梁内所有独立弯矩数相加,可以发现整个轴系最多只存在n-2个独立弯矩,这就造成了弯矩影响系数矩阵的秩最大为n-2,即使轴系上布置超过n-2个测点,最多也只存在n-2个独立方程,若测点布置不合理,比如将所有测点布置在同一跨梁内,独立方程数会低于n-2。
为求解出全部轴承的变位,需对轴系进行处理。若所有跨梁都可以布置测点,选择任意n-2个跨梁各布置一处弯矩测点,并将首个轴承和末轴承的变位设为0,这相当于对轴系整体作刚性约束。整个轴系的变位可以表示为[0 x1x2…xn-10],而轴系实际可能是在此基础上旋转一定角度。这样的旋转不会改变轴承间相对位置,对于轴系校中计算不会产生影响。
与涡轮机等轴系不同的是,船舶推进轴系受现场条件的限制,有部分跨梁,如艉轴管内和主机内部无法布置测点,这样会导致独立弯矩数进一步减少。因此,需要针对这类轴系作出假设。图2与图3分别为单艉轴承和双艉轴承轴系弯矩影响系数的分布情况。

图2 单艉轴承弯矩影响系数图Fig.2 Bending moment influence coefficient for single stern tube bearing shaft

图3 双艉轴承轴系弯矩影响系数图Fig.3 Bending moment influence coefficient for double stern tube bearing shaft
由图2与图3可以看到,对于单艉轴承和双艉轴承轴系,由于测点布置位置受限,轴上独立弯矩数分别为NIB+1与NIB+2,其中,NIB为中间轴承数。为求出所有轴承的变位,对轴系进行如下假设:
1)艉轴管及船艉结构刚度很大,将艉轴管轴承的变位均设为0或已知量。
2)主机内轴段无法布置测点,但考虑到主机轴承一般是整体安装,对于单艉轴承轴系,以弯矩影响系数方程计算中间轴承和1号主机轴承变位,假设其余主机轴承变位与1号主机轴承相同或所有主机轴承按已知倾斜角位于同一直线上;对于双艉轴承轴系,以弯矩影响系数方程计算中间轴承和第1,2号主机轴承变位,假设其余主机轴承与1,2号主机轴承位于同一条直线上。在这样的假设下,通过给定艉轴承高度并补充主机轴承约束,可以通过式(5)和式(6)分别对单艉轴承和双艉轴承进行轴承变位求解。

式中:对于单艉轴承模型,N为NIB+1,对于双艉轴承模型,N为NIB+2;Ln1为第n个主机轴承与第1个主机轴承间的距离;Nmb为主机轴承数;xASTB与xFSTB分别为后艉和前艉轴承给定高度;s为单艉轴承模型中给定的主机轴承倾角,若主机水平安装,则s=0。
2.2 测点优化布置原则
实测中,因操作或者仪器本身的精度问题,测得的弯矩会有一定的误差。将测点布置在跨梁内不同的位置得出的不同求解矩阵对误差的敏感度不同,反映在实际的测试中表现为,即使所有测点的弯矩绝对测量误差都很小,计算出的轴承变位也可能与真实值有很大偏差。因此,在布置测点时,应该选择合理的位置。
为找出可能引起求解矩阵误差敏感度上升的位置,针对图4所示的测点布置方案,研究了误差敏感度与T1~T4这4个测点在各自跨梁内位置的关系,得到图5。其中图5(a)表示误差敏感度随T2,T3测点在同一跨梁内位置变化的情况,图5(b)表示误差敏感度随T1,T4测点在各自跨梁内位置变化的情况。图中误差敏感度是用求解矩阵的条件数表征的,条件数越大,表示矩阵的误差敏感度越大。为便于研究,每次只有2个测点的位置发生改变,其他测点位置保持不变。

图4 测点布置图Fig.4 Arrangement of strain test points
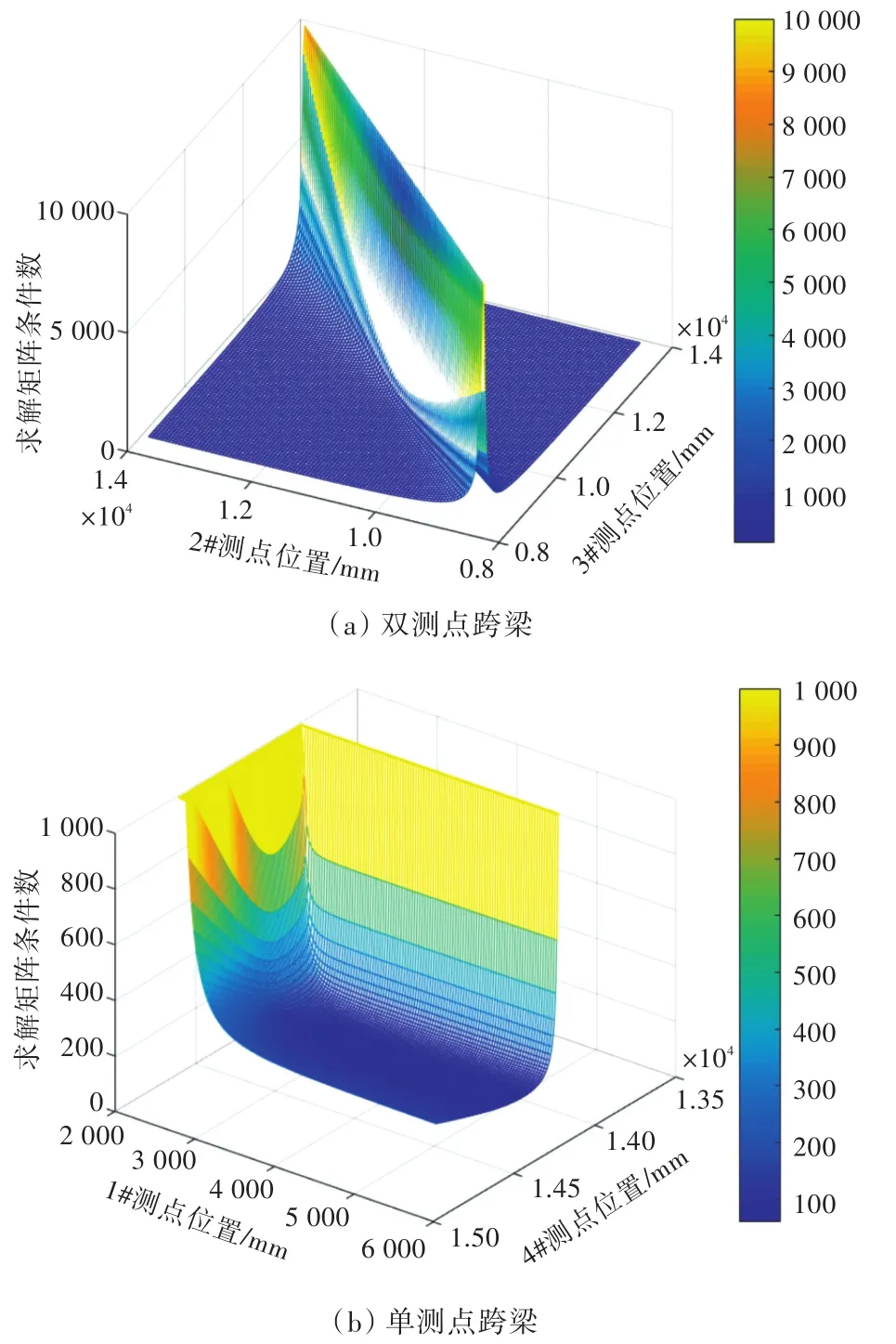
图5 误差敏感度图Fig.5 Plot of error sensitivity
由图5(a)可以看出,若同一跨梁内布置有2个测点,则2个测点的位置相距越近,矩阵条件数越大;当2个测点接近重合时,条件数趋于无穷大。因此,在同一跨梁内布置2处测点时,应增大这2个测点间的距离。
由图5(b)可以看出,T1测点靠近1#轴承时以及T4测点靠近4#轴承时,矩阵条件数都会急剧上升,当测点位置与轴承位置接近重合时,矩阵条件数会趋于无穷大。这是因为当测点位置与轴承重合时,总的独立弯矩数会减1,造成矩阵奇异。因此,若测点位置与轴承重合后独立弯矩数减少,应增大测点与该轴承的距离。
在实际测量中,为提高计算准确度,可以采集超过所需测点数的截面弯矩,通过最小二乘算法(LMS)进行计算,但仍须保证有效测点数不少于该模型需要的独立方程数。
图6是利用弯矩影响系数计算船舶推进轴系安装状态的逆计算流程。

图6 弯矩影响系数法轴系安装状态检验流程图Fig.6 Flow diagram of bending moment influence coefficient method
3 实船验证
根据上文提到的轴系状态逆计算方法,对某38 500 DWT散货船轴系进行了弯曲应变测量,并根据测量结果对轴系状态予以了反推。
3.1 弯矩测量原理
在轴上测点位置粘贴应变片,通过采集轴旋转一周内应变信号的变化,得出轴上对应位置的弯曲应变值,进而得出该位置的弯矩值。具体原理如图7所示。
如图7(a)所示,应变片从水平位置开始随轴旋转,由于轴表面的弯曲应变ε与其距弯曲中性面的距离r成正比。因此,轴旋转一周弯曲应变的波形如图7(b)所示,在不考虑横向弯曲的情况下,该截面处的最大弯曲应变εi为波形最高点与最低点差值的一半[8],如式(7)所示。

图7 轴上弯矩测量原理Fig.7 Principle of measurement for bending moment on shaft

若考虑横向弯曲,则应变的最大、最小值不出现在90°与270°,而是偏离一定的相位,但应变的幅值不会发生变化。
轴上的弯矩可以用式(8)来计算[9]:

式中:Mi为测量截面i处的弯矩,kN·mm;σmax为测量截面i处的最大弯曲应力,GPa;W为测量截面i处的抗弯截面模数,mm3;E为轴系材料的弹性模量,GPa;εi为测量截面i处最大弯曲应变。
弯矩测量具体步骤为:
1)将主机第一缸盘车至上止点位置;
2)在轴上0°与180°位置粘贴2组应变片,组成惠斯通半桥桥路,再将测量电路与数据采集系统连接;
3)利用盘车机将主机盘车一周,同时开始采集数据;
4)利用动态信号采集分析系统对测量数据进行分析,计算各测点的弯矩值。
3.2 模型建立与测点布置
38 500 DWT散货船为双艉轴承轴系,包含1道中间轴承和6道主机轴承,因此需要的有效测点数为3。为验证不同测点位置测得的弯矩对计算结果的影响,在轴上布置了5处测点,将5个测点按每组3个进行组合,可以得出9组逆计算结果。图8为现场布置测点和粘贴应变片的照片,图9为5处测点在轴上分布的示意图。实验测得的5个测点的弯矩值如表1所示。

表1 38 500 DWT散货船轴系应变测试结果Table 1 Tested strain of 38 500 DWT bulk carrier
根据测点弯矩值将测点组合后计算出9组变位,如图10所示。

图10 轴承变位逆计算结果Fig.10 Recalculated bearing offsets
各组合求解矩阵的条件数如表2所示。可见,T1+T2+T4,T1+T2+T5与T3+T4+T5这3组的条件数比其他组大了1~2个数量级,求解矩阵误差敏感度上升,这是因为1号与2号测点相互距离很近、3号测点与中间轴承距离很近。结果T1+T2+T4与T3+T4+T5这2组结果非常不合理,T1+T2+T5组结果也存在较大误差。
去除这3组结果,将其余结果取平均值作为最终结果输出,计算各轴承负荷,如表3所示。
从表3中可以看出,计算负荷与顶举负荷误差最大为3.14%,第1道主机轴承计算为负值,而在实际顶举中也是脱空状态。图11为根据轴承变位计算所得各截面的剪力、弯矩、挠度、转角,可以为全部评估轴系安装状态提供参考。
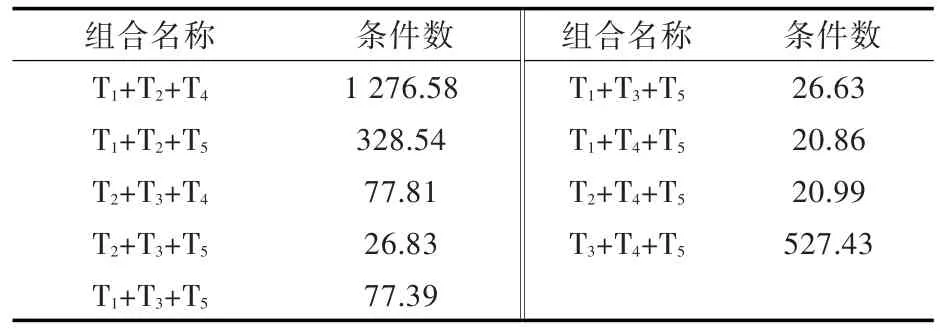
表2 各测点组合求解矩阵条件数Table 2 The condition number under different combinations of measuring points

表3 轴承负荷计算结果Table 3 Calculation results of bearing load

图11 剪力弯矩及挠度转角图Fig.11 Plot for recalculated sheer force,bending moment,deflection and slope on shaft
4 结 语
轴系安装后,获得其准确的安装状态对于安装质量的评估非常重要。本文提出的基于弯矩影响系数的逆计算方法相比传统方法可获得轴系的完整状态,在轴系安装未达标时,其计算出的轴承变位可以为下一步调整提供依据,同时计算出的剪力、弯矩、转角等数据也可对轴系受力状态作更全面的分析。实验结果验证了文中计算方法和测点布置原则的正确性。相比盘车工况的相对静止状态,轴系在实际运转过程中的受力情况将更加复杂,运用无线应变检测技术对轴系实际运转状态的监测是今后很有价值的研究方向。

