基于新型卸荷槽的齿轮泵内部流场及空化特性分析*

李镕熙,周 龙,周振华,万 方,张国庆*

(1.北京理工大学 宇航学院,北京 100081;2.中国航发贵州红林航空动力控制科技有限公司 产品设计所,贵州 贵阳 550009)

0 引 言

航空燃油泵是飞机发动机的关键组成部分,是常见的液压正排量装置,其主要作用是输送航空燃油,其性能的优劣对航空发动机的运行有重要影响。

航空燃油泵的主要类型有齿轮泵、离心泵、柱塞泵等多种结构形式,而齿轮泵有体积小、效率高、结构简单的特点。相比于普通齿轮泵,航空燃油泵具有转速高、流量大、易发生空化现象等特点[1-6]。

有关于齿轮泵内流特性和空化方面的研究一般有3种方法:(1)数学解析法,(2)实验分析法,(3)数值模拟法。因为齿轮泵内流属于复杂的三维非定常流动,理论分析和实验研究周期长、难度大,故主流的研究方法是利用数值模拟法研究齿轮泵流动和空化特性[7-10]。

目前,针对齿轮泵内部流场出现的空化现象进行的研究已有不少。江传惠等人[11]根据实验数据,对齿轮泵内部流场空化初生的原因做出了推断,但是该方法缺少在工程实例中的应用。李晗[12]研究了极限转速下齿轮泵的空化现象,分析了影响齿轮泵流场的各种因素,但是缺少转速对空化现象的影响方面的研究。刘兆领等人[13]研究了特定工况下齿轮泵卸荷槽的设计,并对齿轮泵流场进行了分析,但是缺少工程试验来对该设计效果进行分析验证。王安麟[14]研究了齿轮泵的吸油腔空化现象,并给出了相应的改进方案,发现了该方案不仅可以降低齿轮泵的整体流量,同时也能够提高齿轮泵流场内的流动稳定性;但是该研究也同样缺少试验来对此进行验证。

目前,国内外研究人员对航空燃油齿轮泵内流场空化受转速的影响规律研究较少。因此,笔者设计一种能降低空化影响的新型卸荷槽,并对泵内流场的流动特性进行研究。

首先,笔者对一种新型卸荷槽齿轮泵性能进行分析,然后,在不同转速工况下,针对航空燃油齿轮泵内流特性和空化现象,进行基于Pumplinx软件的数值模拟研究,最后,进行试验验证,以期对今后航空燃油泵的相关设计提供参考。

1 齿轮泵模型

1.1 几何模型

笔者所研究的对象为航空燃油齿轮泵。考虑到齿轮泵倒角等结构对其流场的影响较小,故在实际流场的基础上,笔者对齿轮泵流场模型进行相应的简化。

笔者所采用的流场几何模型由吸油腔、压油腔、齿轮和卸荷槽组成。

齿轮泵流场几何模型如图1所示。

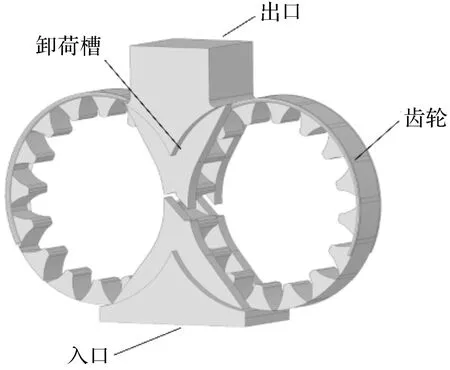
图1 齿轮泵流场几何模型

航空燃油齿轮泵参数如表1所示。

表1 航空燃油泵齿轮参数

笔者设计的新型卸荷槽的几何模型如图2所示。

图2 新型卸荷槽几何模型

航空燃油齿轮泵的卸荷槽参数如表2所示。

表2 卸荷槽参数

1.2 网格与边界条件

齿轮泵内部流场属于三维非定常流动,如果利用一般动网格技术,因为齿轮狭缝狭窄,会导致时间步长太短,计算成本过高。而Pumplinx软件利用二叉树法在出入口及卸荷槽生成笛卡尔网格,通过内置网格生成模块,在齿轮处生成结构网格,可以有效提高计算效率。

在对模型进行前处理时,笔者将啮合轮齿之间的缝隙调至0.05 mm,齿顶和泵体之间的缝隙调至0.04 mm。

齿轮泵网格图如图3所示。

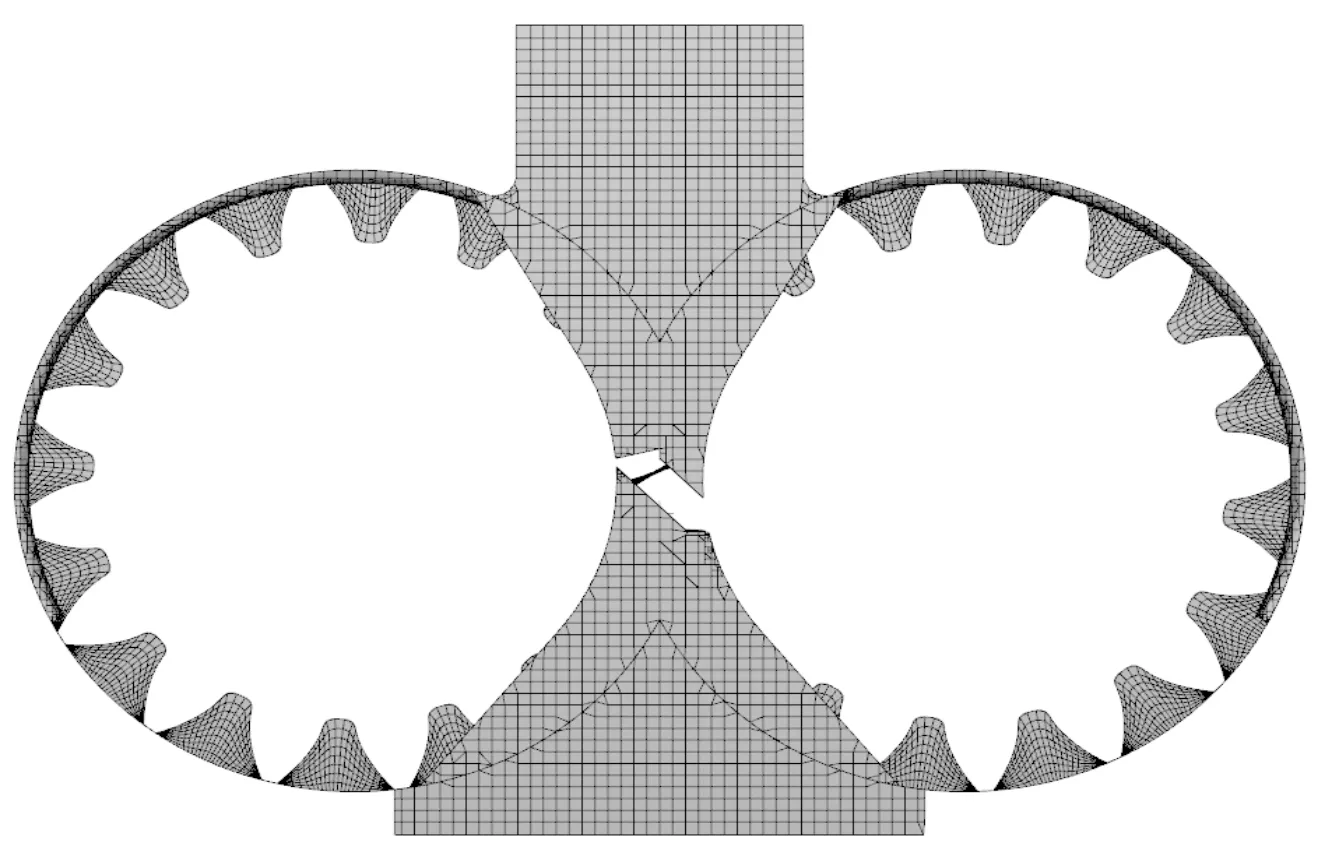
图3 齿轮泵网格图

齿轮泵内流场的边界条件设置如下:

齿轮泵入口边界条件为压力入口,压力值为0.345 MPa;出口边界条件为压力出口,压力值为8 MPa;温度为300 K;齿轮设置为external gear模型;其他壁面设置为静止无滑移壁面;各计算域交界面设置为mismatched grid interface;

流体区域材料为航空煤油,相关物理参数:密度为800 kg·m-3,动力黏度为7×10-3kg·m-1·s-1,气体质量分数为9e-5。

在利用PumpLinx对齿轮泵内部流场进行动态数值计算时,在齿轮泵的转速n=6 000 r·min-1的情况下,齿轮泵旋转周期为T=0.01 s。

为使得到的数据相对准确和稳定,该处模拟齿轮泵的转数为4转,取后2转的结果进行分析,齿轮每转0.75°时,数值计算结果保存一次。

在无卸荷槽和矩形卸荷槽的齿轮泵数值计算中,以及齿轮泵在4种转速n=5 500 r·min-1,n=6 000 r·min-1,n=6 500 r·min-1,n=7 000 r·min-1的数值模拟中,所有设置均与上述相同。

2 数值模拟基础与空化模型

2.1 数值模拟基础

齿轮泵内部流动为非定常不可压缩黏性流动,需要满足质量守恒、动量守恒和能量守恒方程。此处的湍流模型选择标准k-ε模型[15-19]。具体如下:

(1)质量守恒(方程)。

(1)

式中:ρ—流体密度;—哈密顿算子;u—速度矢量。

对于齿轮泵中的不可压缩流体,可化简为:

ρ(·u)=0

(2)

(2)动量守恒方程。

齿轮泵流场满足基于牛顿第二定律的动量方程,即流体控制微元动量的变化率等于该微元体积上质量力和面力之和,其表达式为:

(3)

式中:u,ν,w—x,y,z方向速度分量;μ—动力黏性系数;u—速度矢量;gradu,gradν,gradw—x,y,z方向速度梯度;Su,Sν,Sw—广义动量守恒源项。

(3)能量守恒方程。

齿轮泵流场满足能量守恒定律,即控制微元中能量的增量等于该控制微元吸收的净热量与外力对其做功之和,其表达式为:

(4)

式中:T—流体温度;k—导热系数;cp—定压比热容;ST—流体能量和流体黏性产生的传递能量。

(4)湍流模型。

在Pumplinx数值模拟中,采用标准k-ε湍流模型进行求解,其输运方程为:

Gk+Gb+ρε-Ym+Sk

(5)

(5)

式中:μ—动力黏度;μt—湍动黏度;σk,σε—湍动能和耗散率对应的普朗数;Gk—平均速度梯度引起的湍动能产生项;Gb—浮力湍动能;Ym—总耗散率;C1ε,C2ε,C3ε—经验常数;Sk,Sε—自定义条件。

2.2 空化模型

基于Pumplinx进行数值模拟时,笔者所采用的是全空化模型[20-22]。基于两相流理论,笔者利用Rayleigh-plesset方程描述气泡的析出和溶入,同时利用混合密度概念,其表达式如下:

(7)

式中:ρm—平均密度;ρ1—流体密度;ui—平均速度;fv—气相质量分数;Γ—有效传递系数;pv—气象临界压力;Ce,Cv—经验常数;K—湍流动能。

3 计算结果分析

3.1 新型卸荷槽性能提升

在转速保持6 000 r/min的工况下,笔者对无卸荷槽齿轮泵、矩形卸荷槽齿轮泵和新型卸荷槽齿轮泵进行数值计算,得到相关物理量的分布。

在齿轮的啮合过程中,严重的困油会对齿轮泵出口流量以及流场品质造成影响,而新型卸荷槽能降低该不良影响。

笔者取3种齿轮泵的0.02 s～0.04 s的仿真数据进行后处理分析,利用质量流量和脉动系数来比较各齿轮泵的流量品质。

各类型卸荷槽特征质量流量与脉动系数如表3所示。

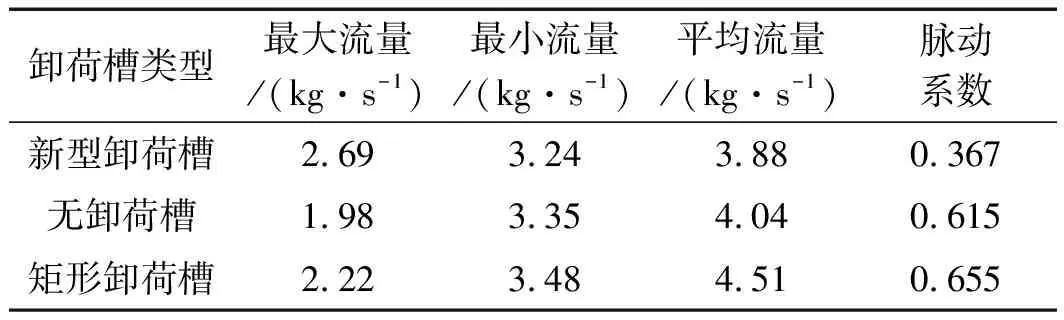
表3 特征质量流量与脉动系数

由表3可知:与无卸荷槽齿轮泵相比,新型卸荷槽齿轮泵的平均流量下降2.99%,脉动系数降低40.32%;与矩形卸荷槽齿轮泵相比,新型卸荷槽齿轮泵的平均流量下降6.89%,脉动系数降低44.61%。

笔者所研究的3种齿轮均为16齿非标准齿轮,因此,在正常工作过程中,对比3种齿轮泵其内部流场的空化情况时,只需要分析一对相互配合的轮齿在转过相同角度过程中泵内的空化情况即可,并取泵第3转初始位置的空化云图进行对比分析。

3种齿轮泵内部流场的总体气体体积分数FT分布情况,如图4所示。

图4 总体气体体积分数FT分布情况

由图4可知:泵的总体气体体积分布主要集中在吸油区和啮合区,新卸荷槽齿轮泵空化范围和强度最小,而无卸荷槽齿轮泵空化现象最为明显;矩形齿轮泵质量流量最大,无卸荷槽的齿轮泵脉动系数最高,新卸荷槽齿轮泵在质量流量损失在7%以内的情况下,减少了流量脉动的44%,有效提高了齿轮泵流场质量。

以上结果证明了新型卸荷槽在降低空化现象方面的高效性,与降低出油口流量脉动方面的有效性,为渐开线外啮合齿轮泵卸荷槽的创新设计提供了一种新的途径。

3.2 转速对齿轮泵流场影响

为实现齿轮泵大流量供油,最有效的途径就是提高齿轮的转速,但高转速易使齿轮泵的空化现象加剧。

笔者对齿轮泵不同转速n=5 500 r·min-1,n=6 000 r·min-1,n=6 500 r·min-1,n=7 000 r·min-1分别进行数值计算,分析齿轮泵内部油液流动规律,研究转速对空化特性的影响。

笔者在泵内设置4个监测点,其中,监测点1位于压油腔,监测点2位于吸油腔,监测点3位于压油腔卸荷槽,监测点4位于吸油腔卸荷槽。

在不同转速下,齿轮泵流场压力的分布如图5所示。

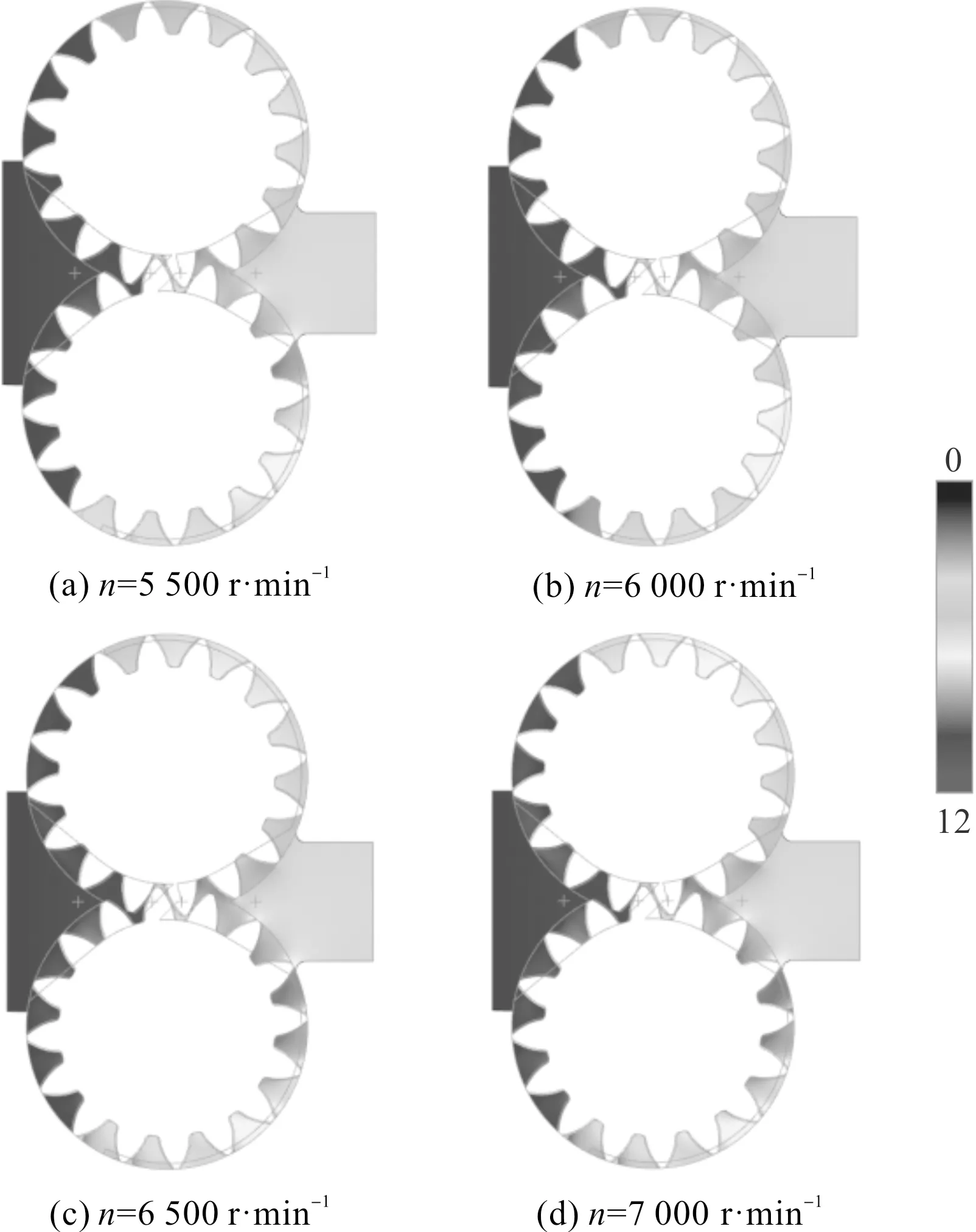
图5 不同转速流场压力分布

由图5可以看出:在高于5 000 r/min转速的情况下,当齿轮处于相同位置时,随着转速n的逐渐上升,齿轮泵内部流场的压力分布情况变化不大;最大压力Pmax出现在压油腔齿轮啮合处,大于出口压力;最小压力Pmin出现在吸油腔齿轮分离处,小于出口压力。

在不同转速下,齿轮泵各监测点压力如图6所示。

图6 齿轮泵各监测点压力

由图6可以看出:在不同转速下,4个监测点的压力的变化幅度不明显,4个监测点的最大压力都随着转速的增加而增加;压油腔的监测点平均压力随着转速的增加而增加,吸油区的监测点平均压力随着转速的增加而减少。

齿轮泵内部的流场流速分布如图7所示。

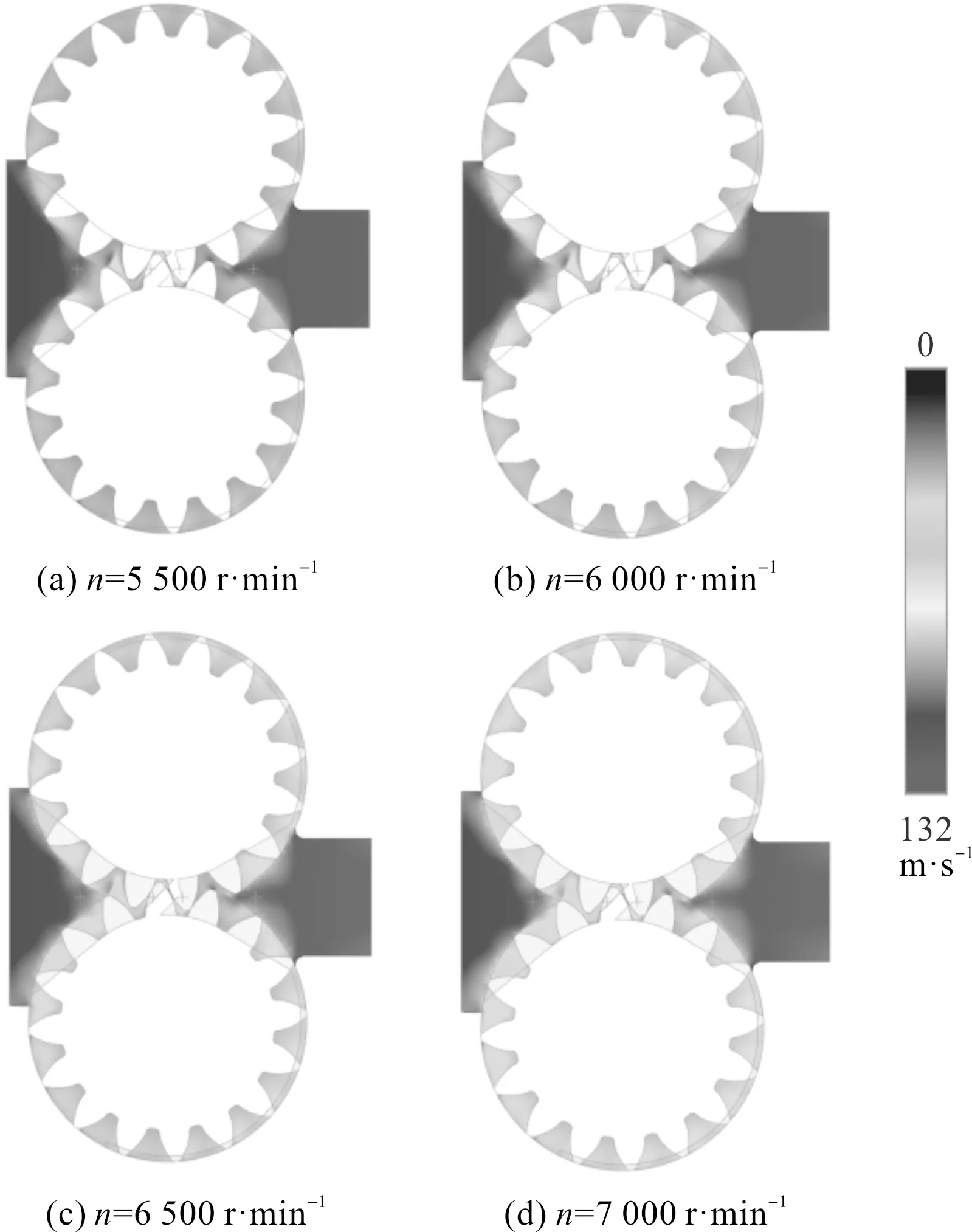
图7 齿轮泵内部流场流速分布

由图7可知:在不同的转速下,齿轮泵的流场流速分布相同,最高流速存在于齿轮的啮合处,其速度远大于齿轮外侧的线速度;在齿轮挤压的作用下,由于啮合处封闭空间的体积急剧变化,啮合处会存在较大的压差。

在不同的转速下,最大流速Vmax如表4所示。

表4 流场最大流速

由表4可知:当齿轮转速逐渐增大,流场的最大速度逐渐增大,但是变化幅度小,转速从5 500 r/min提高到7 000 r/min,流场最大速度仅提高1.38%。这一现象说明,当转速达到一定程度时,流场最大速度增长与齿轮转速增加并非线性关系。

在4种转速下,总体气体体积分数FT如图8所示。

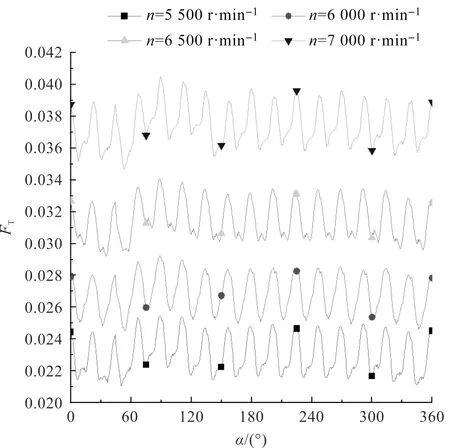
图8 总体气体体积分数FT

由图8知:在每一对轮齿进入啮合,到退出啮合的过程中,齿轮泵内流场的气体体积分数都要经历一次波动,这表明泵内流场的空化程度也会随之经历一次波动;随着转速的逐渐增加,齿轮泵内部流场的气体体积分数的最大值、最小值都在逐渐增大,因此,随着转速的逐渐提高,齿轮泵内部流场整体的空化程度在逐渐增大。

齿轮泵内部流场的总体气体体积分数FT分布情况,如图9所示。

图9 总体气体体积分数FT分布情况

由图9可知：随着齿轮泵转速的提高,齿轮泵啮合处FT的数值和分布范围都在逐渐增大。

4 对比试验

为了验证上述仿真模型的准确性,笔者对新型卸荷槽齿轮泵的质量流量进行测试。

测试中的工作介质为RP-3航空煤油;在出口处安装节流阀以调节出口压力,在节流阀处安装齿轮流量计进行体积流量的测量,随后测量航空煤油密度以得出质量流量;保持温度在规定值的±5 ℃范围内;试验泵由伺服电机驱动。

新型卸荷槽齿轮泵的质量流量试验装置如图10所示在试验过程中,齿轮泵入口压强保持在0.35 MPa,齿轮泵出口压强保持在8 MPa,温度保持在27 ℃,齿轮转速在5 500 r/min,6 000 r/min,6 500 r/min,7 000 r/min。

图10 新型卸荷槽齿轮泵的质量流量试验装置

在4种转速下,出口流量仿真与试验对比如表5所示。

表5 出口流量仿真与试验对比

由表5可知:泵的出口流量与转速呈线性关系,并且误差保持在5%左右。

仿真模型结果与试验结果较为相符,验证了笔者的模型准确性。

5 结束语

由于通过理论分析和实验难以获得高转速航空燃油齿轮泵的内部流场及空化特性,为此,笔者对一种采用了新型卸荷槽结构的航空燃油齿轮泵进行了数值模拟研究。

首先,基于标准k-ε湍流模型与全空化模型建立数学模型,笔者研究了新型卸荷槽齿轮泵的性能;然后,在不同转速下,对新型齿轮泵内流场进行了数值求解,得到了气体体积分数、压力和速度分布,分析了转速变化对流场的影响;最后,搭建了试验平台,进行了不同转速下流量测试,并对仿真结果进行了验证。

研究结论如下:

(1)相比无卸荷槽齿轮泵和传统矩形卸荷槽齿轮泵,在不影响质量流量的情况下,笔者所设计的新型卸荷槽齿轮泵能够有效降低齿轮泵内流场的气体总体体积分数,减弱空化带来的危害;而且能够有效降低齿轮泵的脉动系数,提高其输出流量品质;

(2)在转速较高(大于5 000 r/min)的齿轮泵中,其流场的最大压力(和)最小压力并非位于齿轮泵的出口或入口,而是位于齿轮的啮合处,且最大压力远大于齿轮出口的设计压力。由于受到压差影响,最大的流场速度也出现在齿轮啮合处。因此,在设计高速齿轮泵时,应考虑内流场的压力和速度分布,从而保证产品的寿命和可靠性;

(3)齿轮转速从5 000 r/min提升到7 000 r/min的过程中,齿轮泵内气体体积分数的最大值、最小值和云图所显示的气体分布范围都在逐渐增大,说明齿轮泵内部流场的空化程度也在随之逐渐增大。因此,在提高送油效率而提高转速时,也应考虑空化现象对产品的稳定和寿命的影响。

在今后的研究中,笔者拟根据精确的试验数据,对全空化模型进行修正,使数值模拟结果更加符合高转速航空燃油泵的实际情况,并在此基础上,对其进行进一步的结构优化设计,以便进一步降低齿轮泵的空化现象。