考虑预裂纹的滚动轴承疲劳寿命预测*

张 珂,李青松,夏卫华

(1.上海应用技术大学 机械工程学院,上海 201418; 2.上海人本精密机械有限公司,上海 201411)

0 引 言

轴承是机械设备中的重要部件,其失效可能会导致重大的安全事故的发生[1]。随着工程技术的快速发展,轴承的寿命也有了较大的提升。但在其运转过程中,依然会不可避免地产生裂纹,从而导致整个轴承的失效[2,3]。

在载荷的作用下,轴承的内外圈滚道和滚动体接触部位会产生裂纹。如果在裂纹萌生后继续使用轴承,裂纹可能就会发展成较大的裂缝,最终导致轴承的断裂失效[4,5]。

轴承微观材料失效一般包括裂纹萌生、裂纹扩展、疲劳失效这3个阶段[6,7]。轴承裂纹萌生和裂纹扩展是接触疲劳失效的重要阶段[8,9]。

目前,学者们对轴承的裂纹已经进行了一些研究。谢俊杰等人[10]将损伤力学引入有限元中,以此来对轴承内部裂纹的萌生、扩展、相交进行了仿真,并建立了与实际相符的轴承内部裂纹预测模型。宋宏智等人[11]建立了更准确的内圈损伤—振动耦合轴承性能退化模型,并以该模型来对轴承损伤进行了分析。宋传冲等人[12]运用拉格朗日方程建立了含横向裂纹的转子系统模型,研究了转子系统的非线性动力学行为。刘晓初等人[13]结合理论和有限元方法,分析研究了轴承表面残余应力对滚道接触应力及裂纹扩展速度的影响。

寿命是轴承的主要性能指标之一。然而,目前国内外关于轴承裂纹的研究还存在不足：主要体现在裂纹分析和试验验证方面;多数裂纹研究限于裂纹本身,且局限于应力、应变、动力学分析,并未将裂纹与轴承的疲劳寿命相结合,不能有效地反映轴承的实际寿命,且诸多研究未引入试验验证分析;轴承疲劳寿命相关研究具有较大差距,疲劳寿命影响因素分析单一,寿命预测精度也有高有低。

基于目前的研究缺陷,笔者将轴承裂纹应力、应变等相关研究引入疲劳寿命分析中,并联合疲劳寿命试验进行验证,以提高轴承疲劳寿命预测的准确性。

笔者以行星轮系太阳轮轴传动端轴承为研究对象,在考虑裂纹情况下,对4种不同挡位工况的滚动轴承疲劳寿命进行预测。

首先,分析不考虑裂纹的轴承疲劳寿命;其次,分析预裂纹引入后的轴承疲劳寿命和已有裂纹的剩余疲劳寿命,并进行疲劳寿命试验对比验证,以研究裂纹是否对寿命有较大影响,预裂纹的引入是否使疲劳寿命的仿真预测更接近实际。

1 裂纹扩展寿命理论

笔者运用断裂力学理论对轴承进行疲劳裂纹扩展研究。断裂力学认为,裂纹源于轴承疲劳接触位置[14,15]。

从短裂纹出发,考虑初始裂纹长度为:

x0=(ΔKth/FCEΔεe)2/π

(1)

式中:ΔKth—裂纹门槛应力强度因子;F—几何因子;C—修正因子;Δεe—疲劳应变幅。

针对于缺口根部先产生的裂纹,其所形成的非扩展裂纹的锐缺口疲劳应力集中系数Kf为[16,17]:

(2)

式中:C*—裂纹形状修正因子;D—缺口深度。

Kf考虑缺口尺寸效应。

缺口根部不产生非扩展裂纹缺口的疲劳应力集中系数Kf为[18]:

(3)

等效应力强度因子K为尖端应力强度为[19]:

(4)

修正Paris的Forman公式的疲劳寿命为[20]:

da/dN=[C(K)n]/[(1-R)KC-K]

(5)

式中:a—裂纹尺寸;N—疲劳循环次数;C,n—试验测定材料系数:n=2～4。

假设轴承承受恒定载荷,其载荷为:

(6)

Nf=N-N0

(7)

式中:x0—初始裂纹尺寸,当x0为初始裂纹尺寸,N0=0;af—临界裂纹尺寸;N—循环次数(裂纹扩展至临界尺寸);Nf—轴承疲劳寿命。

2 轴承模型和工况参数

笔者的主要研究对象为无级变速器中行星轮系太阳轮轴传动端轴承,因为该轴承的平稳运行,对整个轴系安全运作具有重要作用。

笔者选取HM1档、HM2档、倒车高速档、倒车低速档等4个不同挡位,对行星轮系太阳轮轴传动端轴承进行分析。

按照倒车低速档、倒车高速档、HM2档、HM1档的挡位次序,转速和径向载荷依次越来越大,HM1档的转速和载荷最大,倒车低速档的转速和载荷最小。

太阳轮轴轴系的模型[21]如图1所示。

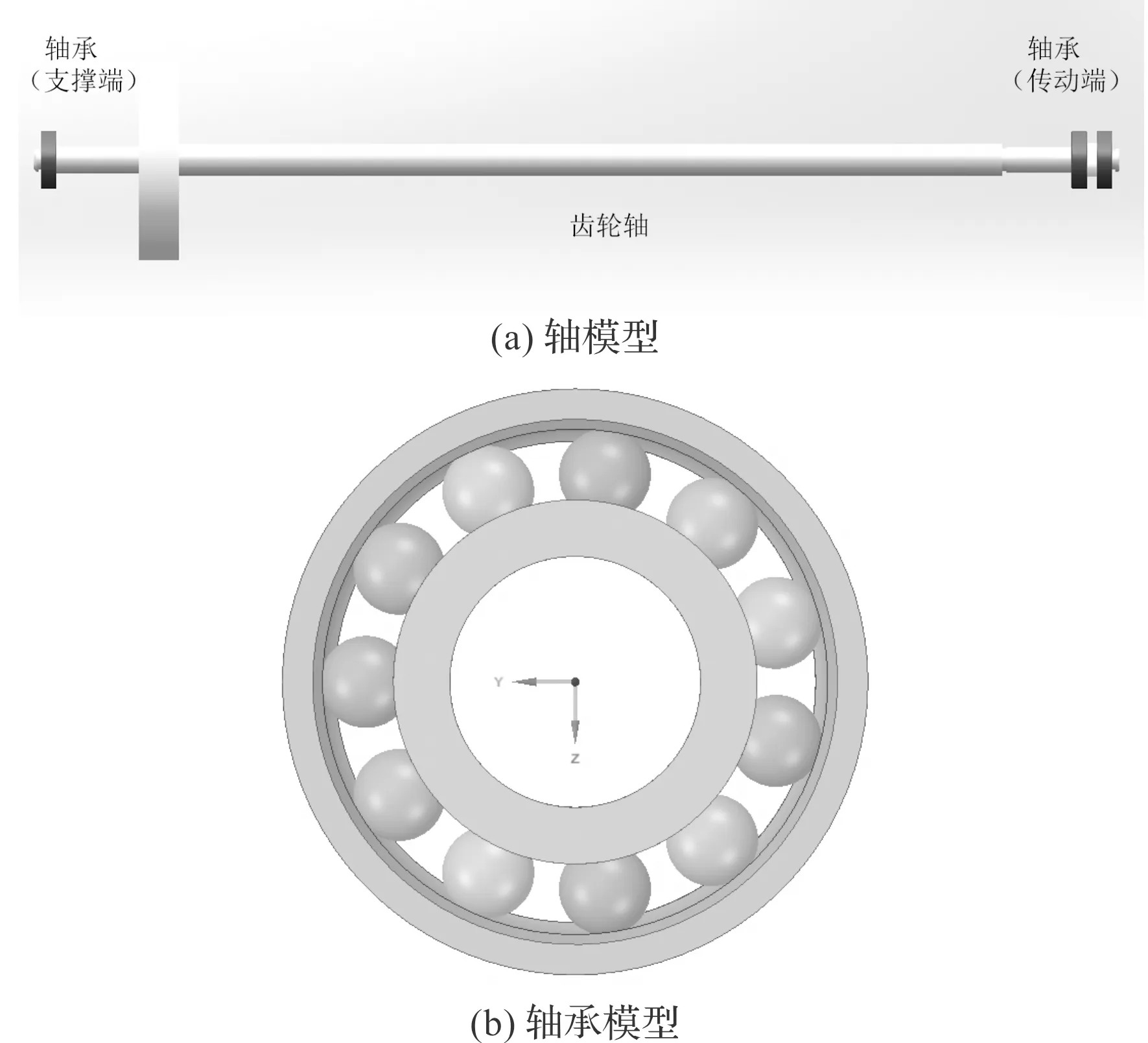
图1 太阳轮轴轴系模型

不同挡位参数的基本工况参数如表1所示[22,23]。

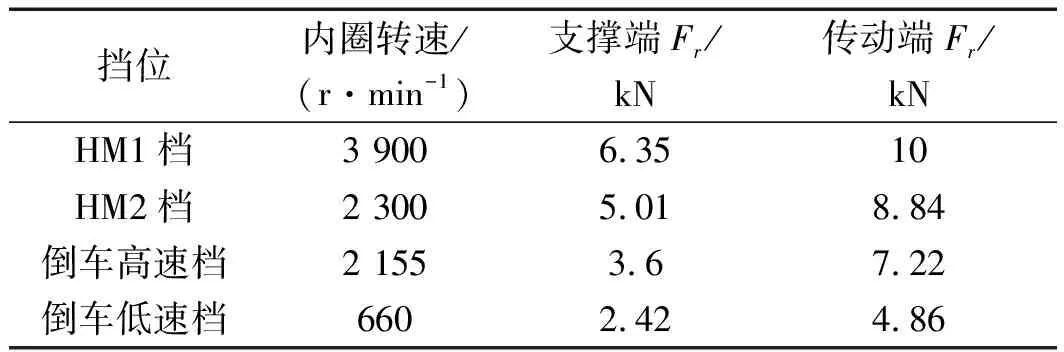
表1 不同挡位轴承工况参数

传动端轴承材料参数如表2所示[24]。

表2 传动端轴承参数

3 轴承疲劳寿命仿真

3.1 不考虑裂纹的轴承寿命分析

此处以传动端6210轴承为例,笔者在SolidWorks软件中,对轴承进行三维建模,再导入ANSYS Workbench中,对其进行前处理和参数设定。

首先,笔者对轴承模型进行网格划分;其次,定义接触(滚动体与内、外圈的滚动接触为摩擦接触;将内圈滚道表面与外圈滚道表面定义成接触面,把滚动体外表面设为目标面);最后,设置边界条件、内圈外表面支撑面,并在内圈施加转动。施加的载荷工况如表1所示。

笔者运用ANSYS Workbench和Fatigue,得到不考虑裂纹的轴承在不同工况下的总形变量云图,如图2所示。

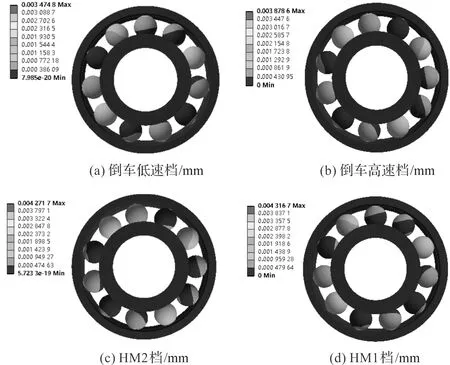
图2 不同工况下不考虑裂纹时轴承的总形变量/mm

由图2可知:在4个挡位工况下,不考虑裂纹时,其最大总变形量可达0.004 316 7 mm,最小总变形量为0.003 474 8 mm。按照挡位次序,转速载荷依次增大,轴承的总变形量也增大。

不同工况下不考虑裂纹时轴承的等效应力云图,如图3所示。

图3 不同工况下不考虑裂纹时轴承的等效应力/MPa

由图3可知:在4个挡位工况下,不考虑裂纹,最大等效应力最大为178.26 MPa,最大等效应力最小为66.849 MPa。按照挡位次序,转速载荷依次增大,轴承的等效应力也增加。

不同工况下不考虑裂纹时轴承的疲劳寿命云图,如图4所示。

图4 不同工况下不考虑裂纹时轴承的疲劳寿命/r

由图4可知:在4个挡位工况下,不考虑裂纹,轴承疲劳寿命最大(倒车低速档)为8.154 1 e+007 r,轴承疲劳寿命(HM1档)最小为1.579 4 e+007 r。按照挡位次序,转速载荷依次增大,轴承疲劳寿命降低。

3.2 考虑预裂纹的轴承寿命分析

3.2.1 预裂纹的生成

笔者在滚动体与内圈接触部位引入预裂纹(前文已给出ANSYS Workbench关于裂纹拓展的计算理论)。笔者在ANSYS Workbench中,插入断裂工具Fracture,选择轴承模型,定义微裂纹尺寸。

《GB—T232—1988金属弯曲试验方法》中所规定的微裂纹尺寸为:长度小于2 mm,宽度小于0.2 mm[25]1-2。

预裂纹生成具有随机性和不确定性。微裂纹的尺寸设定要符合文献[25]1-3的规定选择。预裂纹引入成功合理与否需进行多次仿真数值分析。

首先,笔者选择轴承模型,插入断裂工具Fracture;然后,根据轴承受载情况选择插入椭圆形裂纹,随后设置裂纹参数,选择Generate All Crack Meshes产生裂纹网格。

尖端第一周网格尺寸为裂纹长度的1/9(必须小于1/8),第二圈比例1,分布10个单元,纤维单元节点选择1/4位置,从而实现奇异性。

最后得到可以成功生成的合理裂纹参数为:主要半径为1 mm,小半径为0.1 mm,最大轮廓半径为0.2 mm,裂纹前端分歧定义为30,圆周分歧定义为48,网格轮廓定义为20。

以倒车高速档为例进行多次数值仿真得到成功合理的裂纹参数,如表3所示。

表3 裂纹插入仿真数值分析结果/mm

裂纹定义生成和裂纹网格如图5所示。

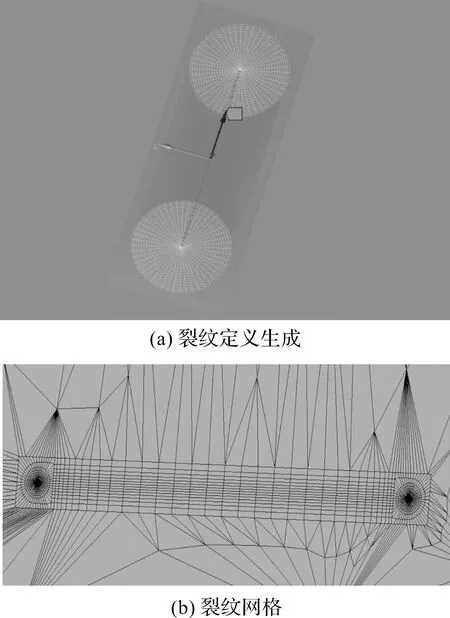
图5 裂纹引入

3.2.2 轴承裂纹尖端仿真结果(局部)

预裂纹引入后,笔者对轴承进行仿真[26]。首先要对裂纹仿真结果进行探讨(对轴承局部放大来分析裂纹)。

轴承裂纹尖端的仿真结果如图6所示。

图6 轴承裂纹尖端的仿真结果

由图6(a,b)可知:参考文献[27,28],并观察裂纹的力学特征可以发现,生成的裂纹存在尖端,整体符合裂纹扩展规律,裂纹整体形貌较好,说明生成的裂纹较为理想;

由图6(c～f)裂纹尖端应力云图可知:按照挡位次序,不同挡位的转速载荷依次增大,裂纹尖端应力逐渐增大。不同挡位下,考虑裂纹和不考虑裂纹相比,两者等效应力仿真数值相差较大。可见,考虑裂纹的等效应力仿真结果大于不考虑裂纹的应力仿真结果。

3.2.3 考虑预裂纹后轴承仿真结果(整体)

预裂纹由萌生到扩展整个周期内,轴承的变形量云图如图7所示。

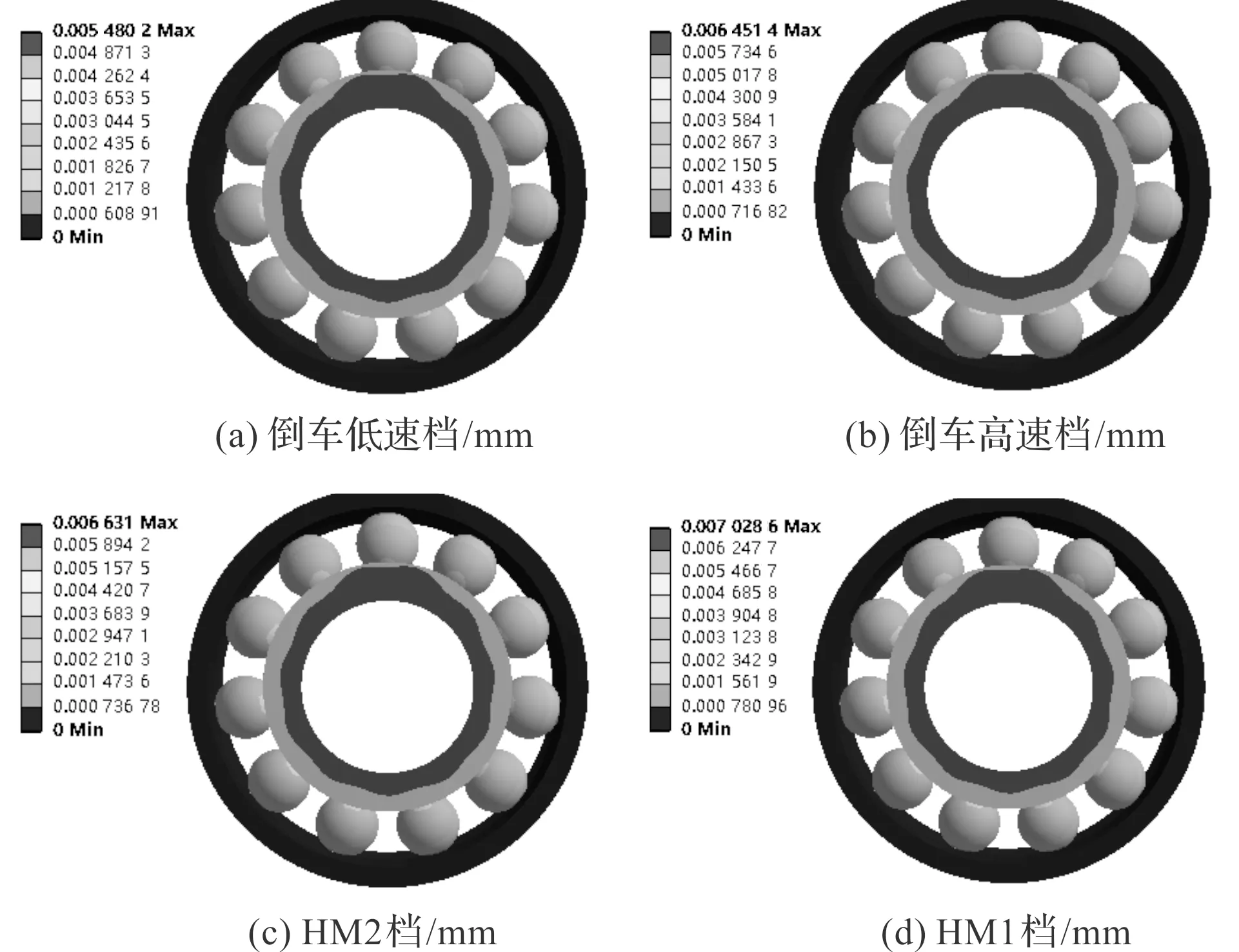
图7 轴承总变形仿真结果(mm)

由图7可知:考虑预裂纹以后,在裂纹萌生至扩展的整个周期内,按照挡位次序,不同挡位转速载荷依次增大,轴承的总形变量也逐渐增大;考虑预裂纹以后,重载高速(HM1档)的形变量最大;

HM1档为最大的总形变量:0.007 080 6 mm,倒车低速档为最小的总形变量:0.005 480 2 mm。

轴承疲劳寿命云图如图8所示。

图8 轴承寿命仿真结果/r

由图8可知:考虑预裂纹以后,在裂纹萌生至扩展的整个过程中,按照挡位次序,不同挡位转速载荷依次增大,轴承疲劳寿命不断减小;考虑预裂纹时,重载高速(HM1档)的轴承疲劳寿命最小;

HM1档为最小的疲劳寿命:9.698 5e+006 r,倒车低速档为最大的疲劳寿命:7.185 3e+007 r。

在不同挡位下,笔者对考虑裂纹与不考虑裂纹的仿真结果进行对比。

不同挡位下,轴承的最大总变形量对比、不同挡位轴承疲劳寿命对比、不同挡位轴承疲劳寿命下降率,如图9所示。

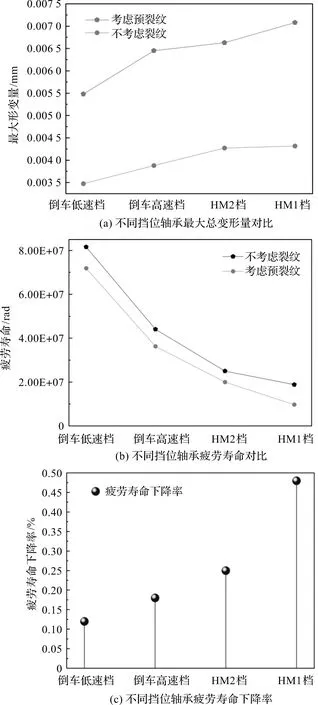
图9 不同挡位下考虑裂纹与不考虑裂纹仿真对比

由图9(a)可知:按照挡位次序,不同挡位转速和载荷依次增大;在裂纹萌生至扩展的整个过程中,预裂纹的引入导致轴承变形量大幅度增加;

由图9(b)可知:由于预裂纹引入,轴承的疲劳寿命出现了大幅下降的趋势;

由图9(c)可知:考虑预裂纹以后,4个不同挡位中寿命下降率最高的(HM1挡)高达48%,寿命下降率最低的(倒车低速档)为12%;考虑预裂纹后,重载高速(HM1挡)的寿命下降率会更大,可见裂纹对轴承的寿命有极大影响。

轴承微裂纹的出现会导致应力、应变、形变量的增大。因此,为避免轴承疲劳寿命下降、寿命使用率降低,减少轴承裂纹是必要的。

3.3 轴承已有裂纹下剩余疲劳寿命分析

上面讨论的是创建预裂纹及裂纹扩展状态下的轴承疲劳寿命,即基于裂纹萌生至裂纹扩展周期内的轴承寿命。

下面将要探讨在已完成裂纹扩展周期状态下,轴承已经产生裂纹时的剩余疲劳寿命。

笔者首先对轴承模型进行修改。以上述各个挡位的等效应力云图为例来确定裂纹位置。最大等效应力在滚动体与内圈接触位置,因此,笔者在内圈外滚道接触位置的最大等效应力处绘制微小弧形沟壑,视作已产生裂纹;探讨已产生裂纹对轴承剩余疲劳寿命的影响,不考虑裂纹引入位置的变化,仅在轴承最大等效应力处绘制插入裂纹来进行剩余疲劳寿命分析。

修改轴承模型后,笔者绘制的裂纹模型如图10所示。

图10 轴承绘制裂纹模型

在SolidWorks软件中,笔者对轴承进行三维建模,并将其导入ANSYS Workbench中进行有限元分析;在有限元软件中,对轴承模型进行网格划分、网格优化,定义接触设置、边界条件、载荷工况条件等相关前处理设置,在计算过程中判别计算收敛性和接触参数是否合理(是否有接触点数量)。

不同工况下,已有裂纹尖端应力演化云图如图11所示。

由图11可知:按照挡位次序,不同挡位的转速和载荷依次增大,裂纹尖端存在应力集中。随着时间推移,不同挡位下轴承裂纹尖端处的应力演化为:尖端应力越来越大,应力集中区域不断扩展,重载高速(HM1档)的尖端应力最大。

图11 已有裂纹尖端应力演化云图/MPa

内圈整体应力云图如图12所示。

由图12内圈整体应力云图可知:等效应力最大部位为绘制裂纹处(滚动体与内圈接触部位),内圈最大等效应力也在裂纹尖端。按照挡位次序,不同挡位的转速和载荷依次增大,内圈等效应力也不断增加。重载高速(HM1档)下,内圈的等效应力最大。

图12 内圈整体应力云图/MPa

通过有限元仿真得到不同挡位工况下,轴承已有裂纹时的剩余疲劳寿命云图[29],如图13所示。

图13 已有裂纹的剩余疲劳寿命/r

由图13可知:按照挡位次序,不同挡位下的转速和载荷依次增大,轴承剩余寿命越来越少。最小值(HM1档)仅为9 326 r,最大值(倒车低速档)为2.090 8e+005 r。

可见高速重载(HM1档)下,如果轴承已经产生裂纹且继续使用,则轴承达到疲劳寿命极限的时间越短。

笔者对轴承剩余疲劳寿命结果进行分析。

不同挡位下,剩余疲劳寿命、不同挡位剩余疲劳寿命占比,如图14所示。

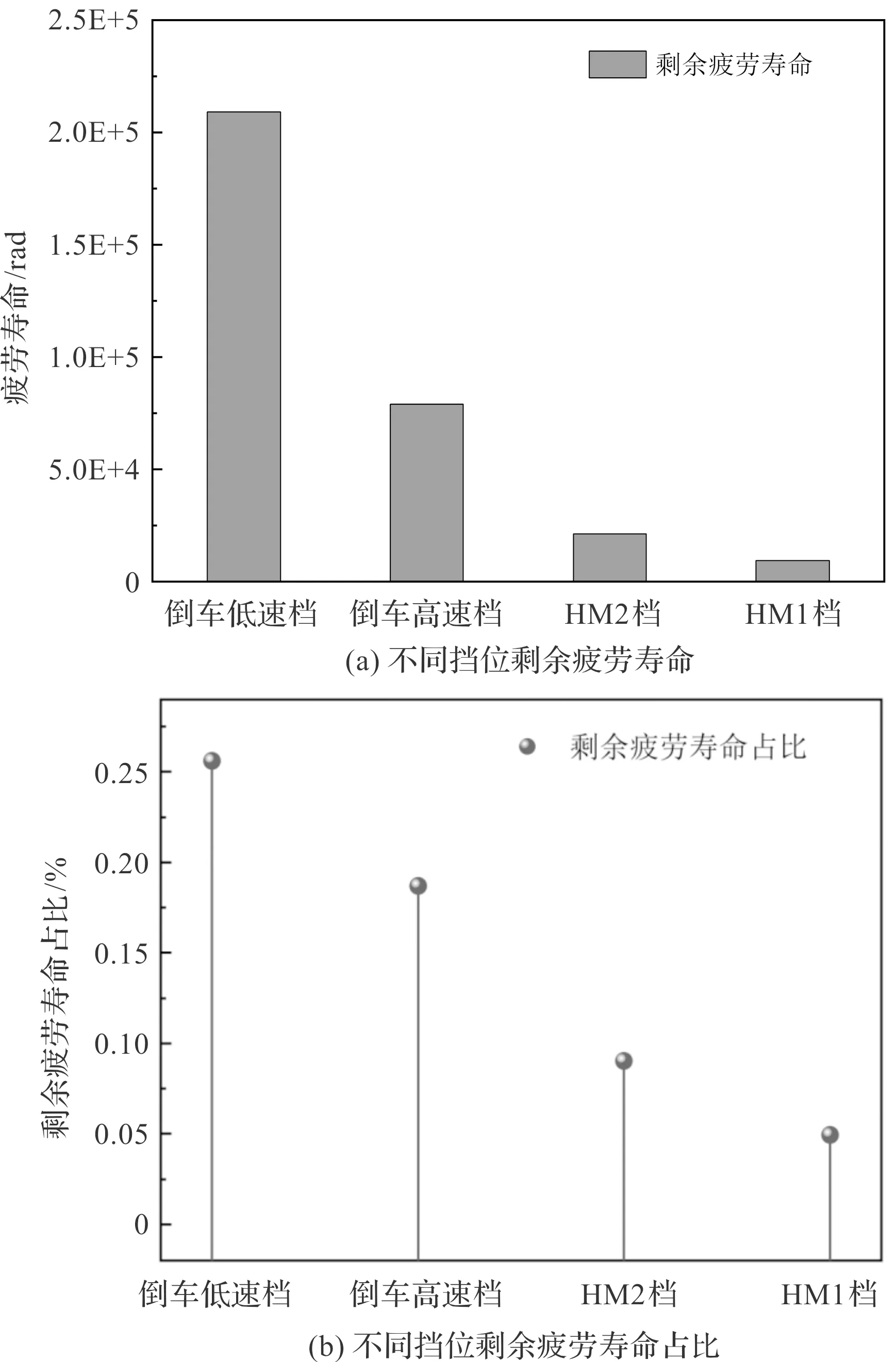
图14 剩余疲劳寿命分析

由图14(a)可知:按照挡位次序,不同挡位下的转速和载荷依次增大,轴承剩余疲劳寿命越来越少。

图14(b)的百分比表示为:当轴承已有裂纹时的剩余疲劳寿命,占不考虑裂纹时的仿真疲劳寿命的比例。

可以看出,当微裂纹已经产生时,如果轴承依然继续使用,那么倒车低速档剩下0.257%的寿命,倒车低速档剩下0.187%的寿命,HM2档剩下0.090 3%的寿命,HM1档剩下0.059%的寿命。高速重载(HM1档)下,剩余疲劳寿命占比最小。

因此,如果检测到轴承裂纹产生时,应及时更换轴承,以避免较大的安全事故。

4 轴承疲劳寿命试验

6210深沟球轴承主要用于汽车传动轴,故笔者在滚动轴承疲劳寿命试验机上完成其试验。

轴承试验工况条件为:试验中,自身脂润滑,选取2个典型的高速档位(HM1档和倒车高速档工况)进行试验。

轴承疲劳寿命试验中的失效判据为:轴承振幅增大,并出现规律性尖峰波(试验中,如出现轴承接触表面疲劳剥落、压痕、局部损伤,轴承振幅会明显增大);轴承振幅在60 μm～100 μm视为轴承失效,应停机检测。

疲劳试验预期为:轴承发生疲劳破坏,则停止试验,并记录其疲劳寿命。

4.1 疲劳寿命试验机

轴承疲劳寿命试验机是需要施加载荷后,对滚动轴承进行旋转疲劳寿命试验的机器。T20-60-nf滚动轴承疲劳寿命试验机具有自动测控、高测试精度的特点。

轴承疲劳寿命试验机如图15所示。

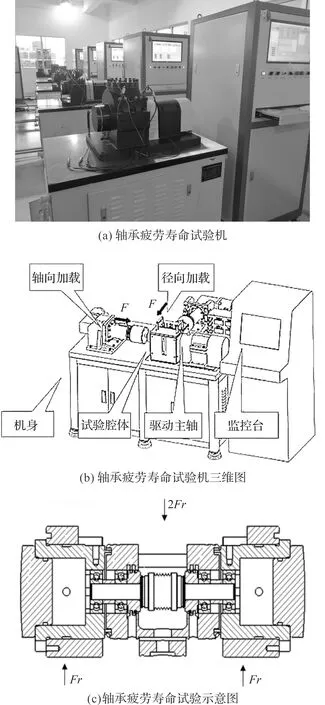
图15 T20-60 nf滚动轴承疲劳寿命试验机

4.2 疲劳寿命试验结果分析

笔者在典型高速档位(HM1档和倒车高速档)下,进行轴承的疲劳寿命试验。

HM1档试验结果如表4所示。

表4 HM1档试验数据结果

倒车高速档试验结果如表5所示。

表5 倒车高速档试验数据结果

轴承失效图如图16所示。

图16 轴承失效图

由表(4,5)及图16可知:NO.1轴承内圈滚道剥落,NO.2轴承外圈滚道有轻微压痕微裂纹,NO.5轴承内圈沟道剥落微裂纹,NO.6轴承外圈滚道压痕微裂纹,NO.8轴承油脂干结。

由此可以看出:导致轴承疲劳失效的主要原因是滚道发生剥落;发生剥落的位置为内外圈滚道,即滚动体与内外圈接触部位。

4.3 寿命试验结果和仿真结果对比

由疲劳寿命试验结果可知:造成轴承发生疲劳损坏的主要原因为疲劳剥落,失效位置基本为滚动体与内外圈接触的滚道。

疲劳寿命试验结果和不考虑裂纹仿真结果对比,如表6所示。

由表6可知:不考虑预裂纹的轴承仿真预测疲劳寿命,与轴承试验疲劳寿命结果对比存在一定的误差;轴承仿真寿命Lf均大于轴承试验寿命Ls。

轴承寿命具有离散性,且差异较大。因材料疲劳本身具有离散性,结构、尺寸、材料、加工工艺等完全相同的轴承在相同的工况下,寿命差异较为明显,误差也在所难免。

因此,笔者去除粗大误差后再次进行对比。通过对比不难发现:仿真与疲劳寿命试验的平均误差为8.14%,误差较小。说明笔者针对滚动轴承不考虑裂纹进行的疲劳寿命分析所建立的有限元模型是有效的。

在试验的两个工况下:HM1挡位下的轴承平均疲劳寿命为1.482 1e+007 r;倒车高速挡位下的轴承平均疲劳寿命为3.861 0e+007 r。

在轴承疲劳寿命试验过程中,由于NO.2、NO.5、NO.6这3个轴承试件产生了裂纹现象,笔者将NO.2、NO.5、NO.6这3个试件的疲劳寿命试验结果和考虑预裂纹仿真结果进行了对比,其结果如表7所示。

表7 考虑预裂纹仿真结果和疲劳寿命试验结果对比

由表7可知:轴承仿真寿命Lf均小于轴承试验寿命Ls,这是因为轴承仿真考虑预裂纹时,仿真裂纹参数设定要比真实的轴承裂纹效应大(可以通过调整裂纹参数,使裂纹仿真更趋近于真实裂纹);

但从表7的误差结果来看:考虑预裂纹的轴承仿真预测疲劳寿命与轴承试验疲劳寿命结果存在一定的误差,且误差较小,说明上述预裂纹引入的仿真模型依然是合理的。

由表(6,7)可知:NO.2、NO.5、NO.6这3个轴承试件不考虑预裂纹的仿真结果和疲劳寿命试验结果的对比误差依次为:40%、9.21%、8.37%;NO.2、NO.5、NO.6这3个轴承试件考虑预裂纹的仿真结果和疲劳寿命试验结果的对比误差依次为:13.5%、5.9%、6.63%;

NO.2轴承不考虑裂纹和考虑预裂纹两者分别与疲劳寿命试验结果的对比,误差由40%减小到13.5%,误差减小26.5%;

NO.5轴承不考虑裂纹和考虑预裂纹两者分别与疲劳寿命试验结果的对比,误差由9.21%减小到5.9%,误差减小3.31%;

NO.6轴承不考虑裂纹和考虑预裂纹两者分别与疲劳寿命试验结果的对比,误差由9.21%减小到8.37%,误差减小0.9%;

不考虑裂纹与考虑预裂纹相比:3个轴承考虑裂纹时仿真寿命和试验寿命的误差,小于不考虑预裂纹时仿真寿命和试验寿命的误差。

由此可以看出:预裂纹的引入使轴承疲劳寿命的仿真预测更接近轴承实际寿命,也说明考虑预裂纹的轴承寿命的仿真预测模型是有效的。

5 结束语

为了研究裂纹对轴承疲劳寿命的影响,笔者以行星轮系太阳轮轴传动端深沟球轴承为研究对象,针对4种不同挡位工况进行了裂纹分析,探讨了轴承裂纹对轴承疲劳寿命的影响。

笔者首先对不考虑裂纹的轴承寿命结果进行了分析,然后对考虑预裂纹的轴承寿命结果进行了分析,并进行了分析结果的对比;之后,基于已有裂纹,仿真分析了轴承已经产生微裂纹状态下的剩余疲劳寿命;最后,对轴承疲劳寿命进行了试验验证分析。

研究结论如下:

(1)预裂纹的引入对轴承寿命的影响比较大。预裂纹引入导致轴承的变形量大幅度增加,轴承的寿命大幅度下降。在不同挡位,寿命下降率最高达48%;

(2)不考虑裂纹与考虑预裂纹相比,NO.2、NO.5、NO.6这3个轴承试件考虑裂纹的轴承仿真寿命和轴承试验寿命的误差逐渐减小,预裂纹的引入使轴承疲劳寿命的仿真预测更接近轴承的实际寿命;

(3)若在裂纹已经产生时继续使用轴承,则倒车低速档还剩下0.257%的寿命,倒车低速档还剩下0.187%的寿命,HM2档还剩下0.090 3%的寿命,HM1档还剩下0.059%的寿命;

(4)在高速重载下,考虑裂纹的疲劳寿命和轴承已有裂纹时的剩余疲劳寿命都是最小的,裂纹产生时应及时更换轴承。

综上所述,轴承裂纹的出现会导致应力、应变、形变量的增大,也会导致疲劳寿命的降低。因此,为了避免轴承寿命使用率降低,减少轴承的裂纹是必要的;此外,检测到裂纹出现以后应及时更换轴承。

后续,笔者将采用光学显微镜,对裂纹进行观察,基于裂纹机理来分析裂纹微观组织,从微观角度来探讨轴承的断裂疲劳特性;基于多尺度位错动力学,模拟轴承裂纹位错的演化特征;分析裂纹产生的原因,避免缺陷产生,从而提高轴承疲劳寿命。