双渐开线齿轮柔性多体动力学分析*

潘 毅,许妍妍,樊智敏

(青岛科技大学 机电工程学院,山东 青岛 266061)

0 引 言

齿轮传动装置是机械装备中应用最广泛的动力传递装置,其力学性能及动力学特性直接影响整个机械设备的性能。

在实际工况下,齿轮在传动过程中并不是绝对的刚体,在接触时会表现出一定的柔性体特征。柔性多体动力学建模可以较为真实地模拟齿轮的实际动态特性,即通过模态分析的方式,将双渐开线齿轮柔性化,并结合ADAMS对其进行动力学仿真。综合考虑弹性变形及振动对双渐开线齿轮动力学特性的影响可知,齿轮柔性化后的弹性变形及振动,可以降低齿轮的传动误差。

姚廷强等人[1]建立了刚柔耦合齿轮动力学模型,通过控制变量的方法,对齿轮传动过程的振动特性进行了研究。路亮等人[2]对刚柔耦合齿轮箱进行了研究,分析了其故障原理与动态响应特性,并将该结果与实验结果进行了对比,验证了该刚柔耦合模型的准确性。许俊梅等人[3]研究了刚体齿轮传动过程啮合力的变化情况。李瑶[4]研究了摩擦情况下的刚体齿轮动力学特性。陈勇等人[5]研究了齿轮在疲劳点蚀情况下,刚体齿轮的动力学特性,并将该结果与实验结果进行了对比。胡明明等人[6]研究了采煤机截割部的刚柔耦合动力学特性,对比纯刚体与刚柔耦合模型的传动特性,得出了柔性体齿轮啮合传动时的最大应力。侯玉洁等人[7]研究了变位齿轮刚体模型的动力学特性。郝驰宇等人[8]研究了考虑刚柔耦合的行星齿轮故障动态特性。王敏等人[9]基于有限元思想,对蜗杆进行了模态分析,研究了齿轮箱蜗杆副的接触变形。柴文杰[10]基于柔性体多体动力学,研究了谐波齿轮的变形情况,并总结了谐波齿轮的变形规律。

分阶式双渐开线齿轮是综合渐开线齿轮与双圆弧齿轮优点的一种新型齿轮[11],这种齿轮的工作齿廓由两段相错的渐开线组成,中间以一段圆弧包络过渡曲线连接而成,其齿顶与齿根两段渐开线齿廓呈阶梯式分布。分阶式渐开线齿轮常简称为双渐开线齿轮(下同)。

许君君等人[12]基于有限元思想进行了齿轮模态分析,研究了齿面摩擦与啮合刚度对双渐开线齿轮动力学特性的影响;但是该研究仅考虑了齿轮自由模态下的振动变形,而忽略了齿轮传动过程中柔性体接触带来的弹性变形。张秀文等人[13]基于分形理论建立了双渐开线齿轮接触刚度分形模型,研究了双渐开线的动态接触应力;但是在有限元分析过程中,未考虑柔性体齿轮弹性变形及振动对其接触力的影响。

目前针对双渐开线齿轮动力学方面的研究多忽略齿轮的柔性体特征,因此,双渐开线齿轮传动过程的动态特性与接触变形研究的准确性受到了影响。

因此,笔者将双渐开线齿轮柔性化,并进行动力学仿真,综合考虑弹性变形与振动对双渐开线齿轮传动角速度、角加速度、啮合力的影响,为减少柔性体齿轮传动过程中受到的振动与冲击提供参考;用动力学仿真结合模态分析,研究齿轮传动过程中的轮齿变形,对比分析双渐开线齿轮与普通渐开线齿轮的轮齿变形,既总结双渐开线齿轮传动变形特点,也为齿轮传动变形误差优化设计提供参考。

1 刚柔耦合动力学理论

1.1 广义坐标的选择

动力学方程的求解速度很大程度上基于广义坐标的选择。

研究刚体在惯性空间的运动时,一般用其质心笛卡尔坐标和反映刚体方位的欧拉角作为广义坐标,即:

(1)

式中：qi—刚体的广义坐标矩阵；x,y,z—刚体的笛卡尔坐标；σ,θ,φ—x,y,z轴的角位移；q—多体系统的广义坐标矩阵。

由于采用了不独立的广义坐标,系统动力学方程虽然是最大数量,但却是高度稀疏耦合的代数方程,应采用稀疏矩阵的方法进行高效求解。

1.2 柔性体理论

柔性体系统中的坐标系,即柔性体变形模型如图1所示。

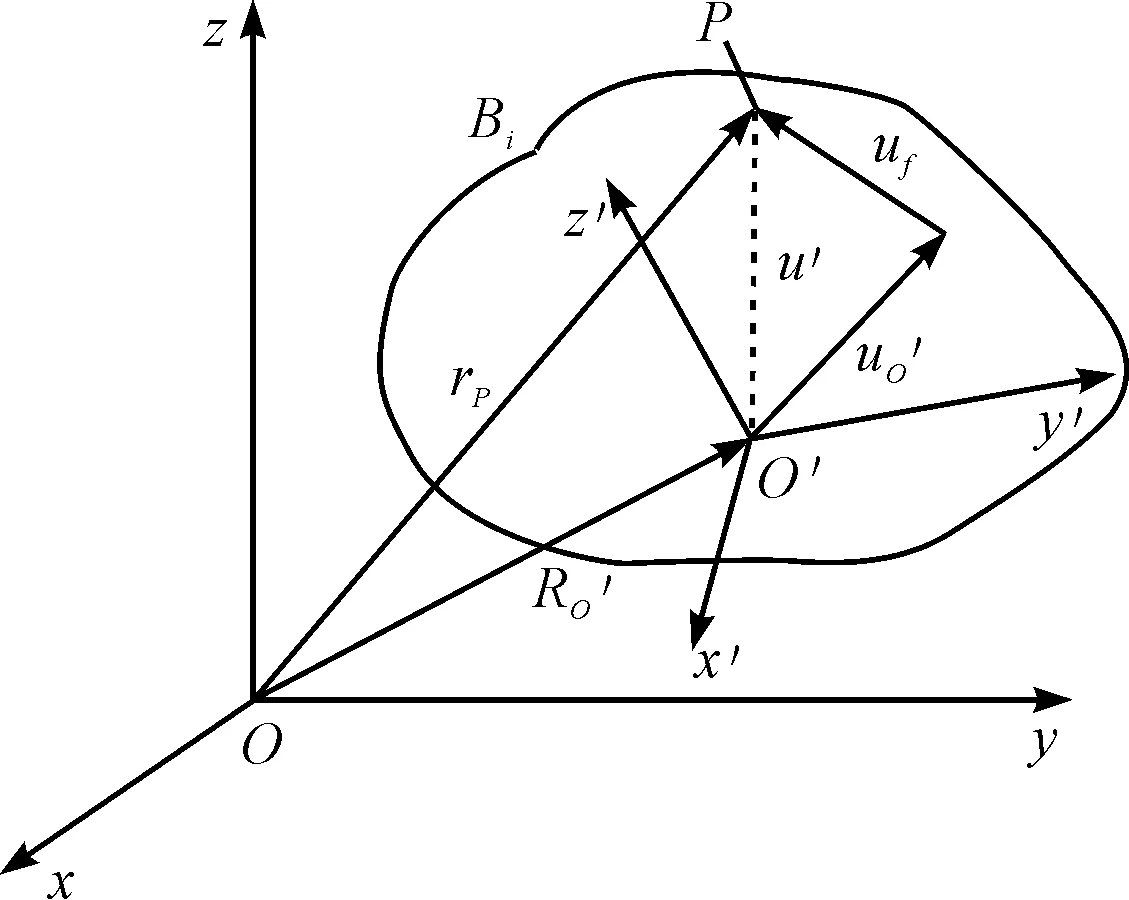
图1 柔性体变形模型

图1中，包括惯性坐标系oxyz和浮动坐标系o′y′x′z′，建立在柔性体上的浮动坐标系用来描述柔性体的运动；浮动坐标系可以相对惯性坐标系进行有限的移动和转动；浮动坐标系在惯性坐标系中的坐标(移动、转动)称为参考坐标。

在分析柔性体的运动时，尤其是在小变形的情况下，可以将其运动过程近似地分解为刚性移动、刚性转动、变形运动的合成运动。

图1中，柔性体上任意点P的位置向量为：

rp=Ro′+Au′=Ro′+A(uo′+uf)

(2)

式中：rp—P点在惯性坐标系中的向量；Ro′—浮动坐标系原点在惯性坐标系中的向量；A—浮动坐标系对惯性坐标系的旋转变换矩阵；u′—变形后在浮动坐标系中的向量；uo′—柔性体未变形时P点在浮动坐标系的位置向量；uf—相对变形引起的位置向量。

式(2)中，对时间取一阶和二阶导数，可得到柔性体上任一点的速度向量及加速度向量[14-18]为：

(3)

(4)

2 双渐开线齿轮动力学模型的建立

2.1 刚体齿轮动力学模型

研究其柔性体齿轮动力学特性,是评价双渐开线齿轮传动动态特性的重要依据。

双渐开线齿轮端面齿廓如图2所示。

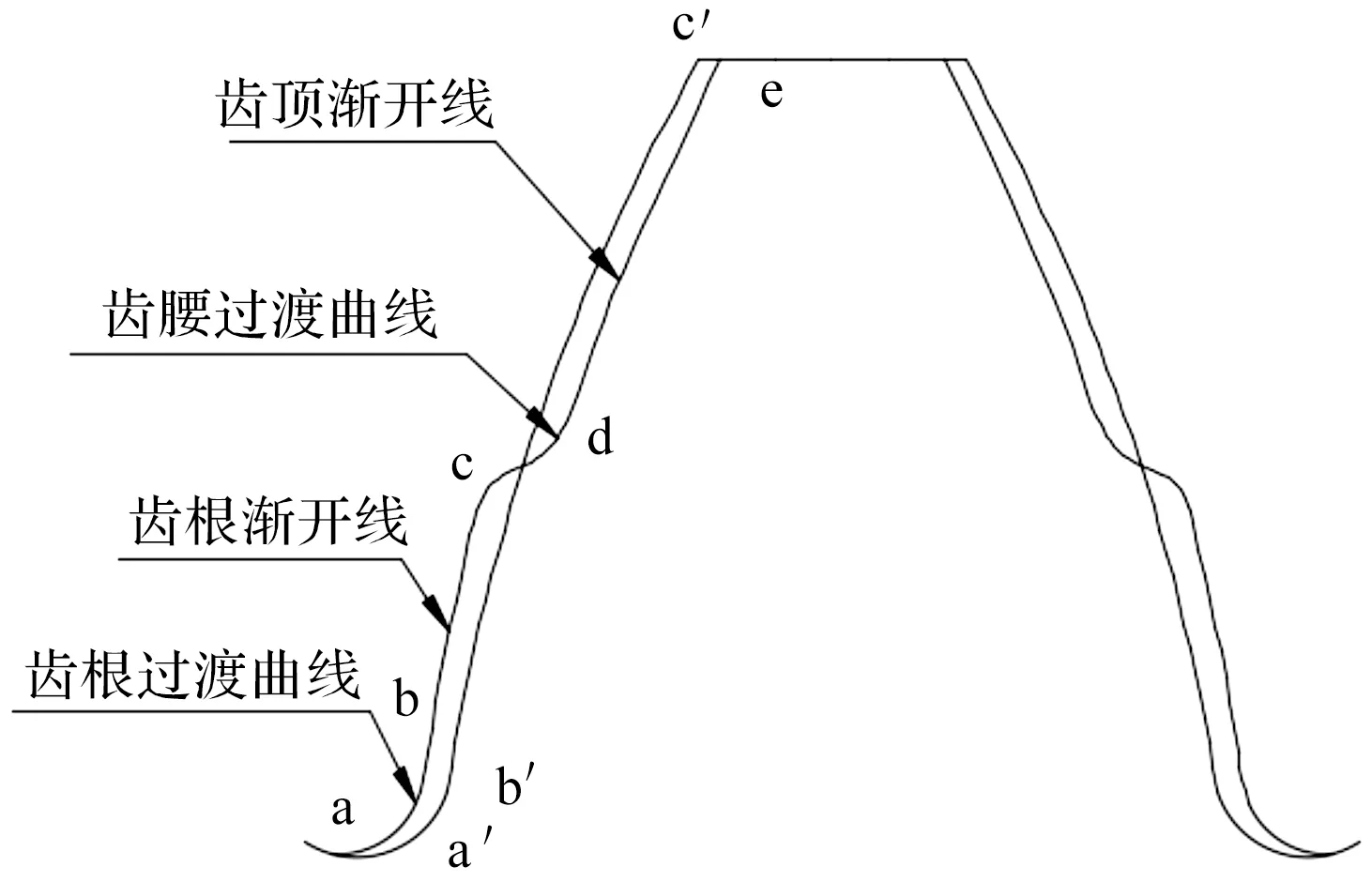
图2 双渐开线齿轮端面齿廓

双渐开线齿轮的基本参数如表1所示。

表1 双渐开线齿轮基本参数

利用SolidWorks,笔者根据表1齿轮参数建立齿轮三维模型,并结合多体学仿真软件ADAMS,按照实际的传动关系,对主动轮与从动轮施加约束,具体的步骤如下:

(1)主动轮与从动轮分别与大地坐标系设置旋转副,共两对;

(2)在主动轮与从动轮之间设置接触力;

(3)在主动轮上设置向下,即Y方向的重力;

(4)在主动轮上设置驱动转速;

(5)在从动轮上设置负载转矩。

生成的双渐开线齿轮刚体刚体动力学模型如图3所示。

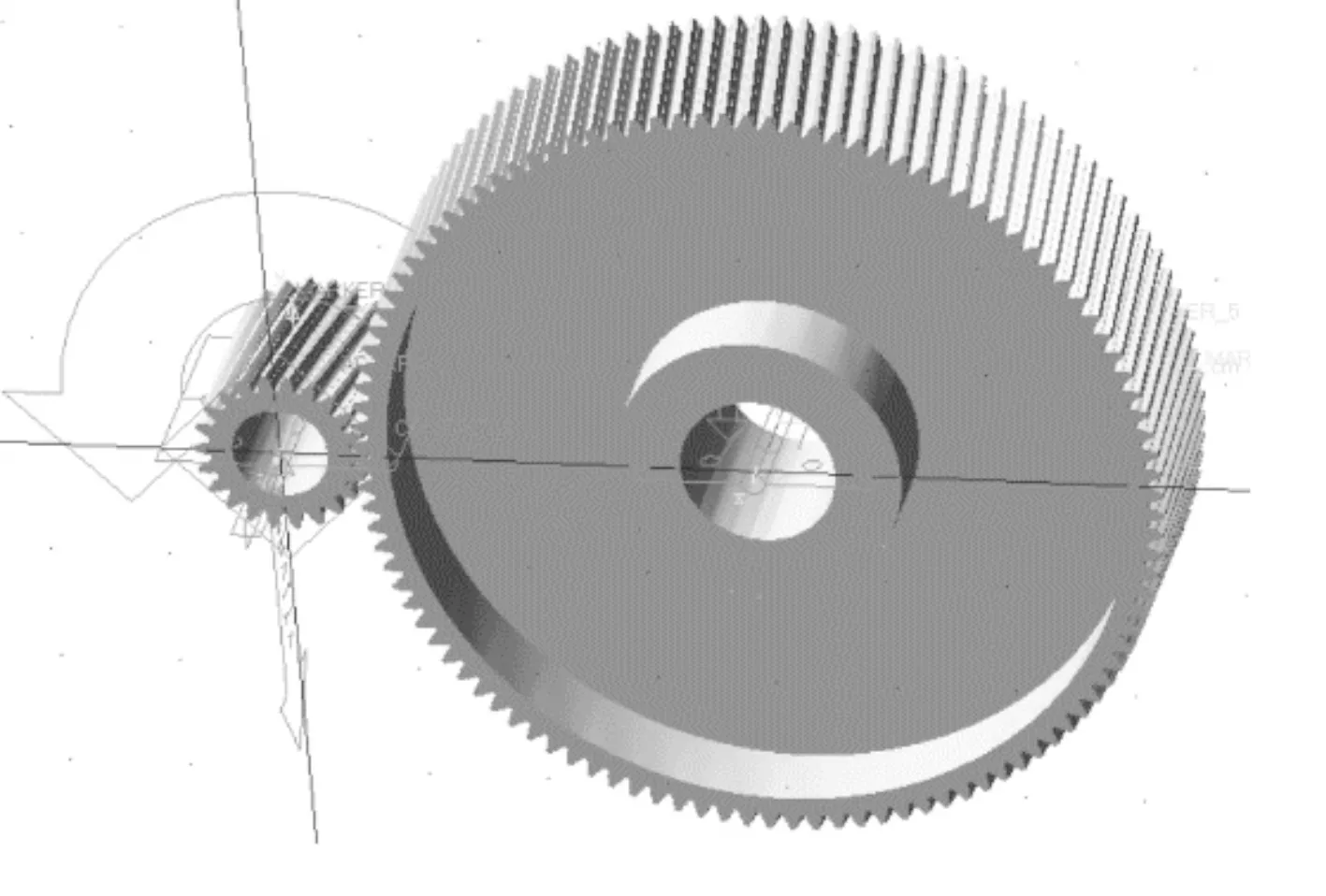
图3 双渐开线齿轮刚体动力学模型

2.2 接触力参数的设定

在仿真过程中,笔者应用ADAMS中的Impact函数计算接触力,其函数表达式[5]2-3为:

(5)

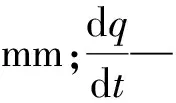
撞击时的接触法向力F为：

F-impact=

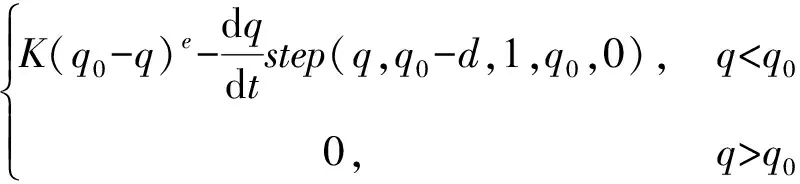
(6)

根据Hertz弹性接触理论，有：

(7)

式中：δ—变形量。

由上式可得撞击时接触法向力F与变形量δ的关系为：

F=Kδ3/2

(8)

(9)

式中：R—齿轮副接触处的综合曲率半径。

其中，刚度系数K的大小受到不同材料属性与碰撞接触表面几何形状的影响。

双渐开线齿轮的综合曲率半径为[13]151-152:

(10)

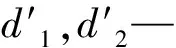
该处所用材料为45号钢，其弹性模量可通过下式计算得到：

(11)

式中：μ1,μ2—两齿轮的泊松比；E1,E2—两双渐开线齿轮材料的弹性模量。

动力学仿真参数如表2所示。

表2 动力学仿真基本参数

2.3 柔性体齿轮动力学模型的建立

笔者将ADAMS中的刚体齿轮动力学模型导入ANSYS中,对齿轮模型进行柔性化处理;并在ANSYS中完成其材料属性及网格划分的设置(其中,材料选择45号钢,网格划分选择六面体单元)。

经网格划分后得到的双渐开线齿轮模型,如图4所示。

图4 ANSYS网格划分模型

笔者利用APDL指令进行模态分析,生成模态中性文件MNF文件,再利用ADAMS中的Flex模块,将MNF文件导入到ADAMS中。

由于原有刚体齿轮动力学模型的约束会消失,此处需要重新进行设置。与之前不同的是,柔性体齿轮动力学模型中的接触力设置,选择的是柔性体与柔性体接触,其他动力学仿真参数不变。

最后生成的柔性体齿轮动力学模型如图5所示。

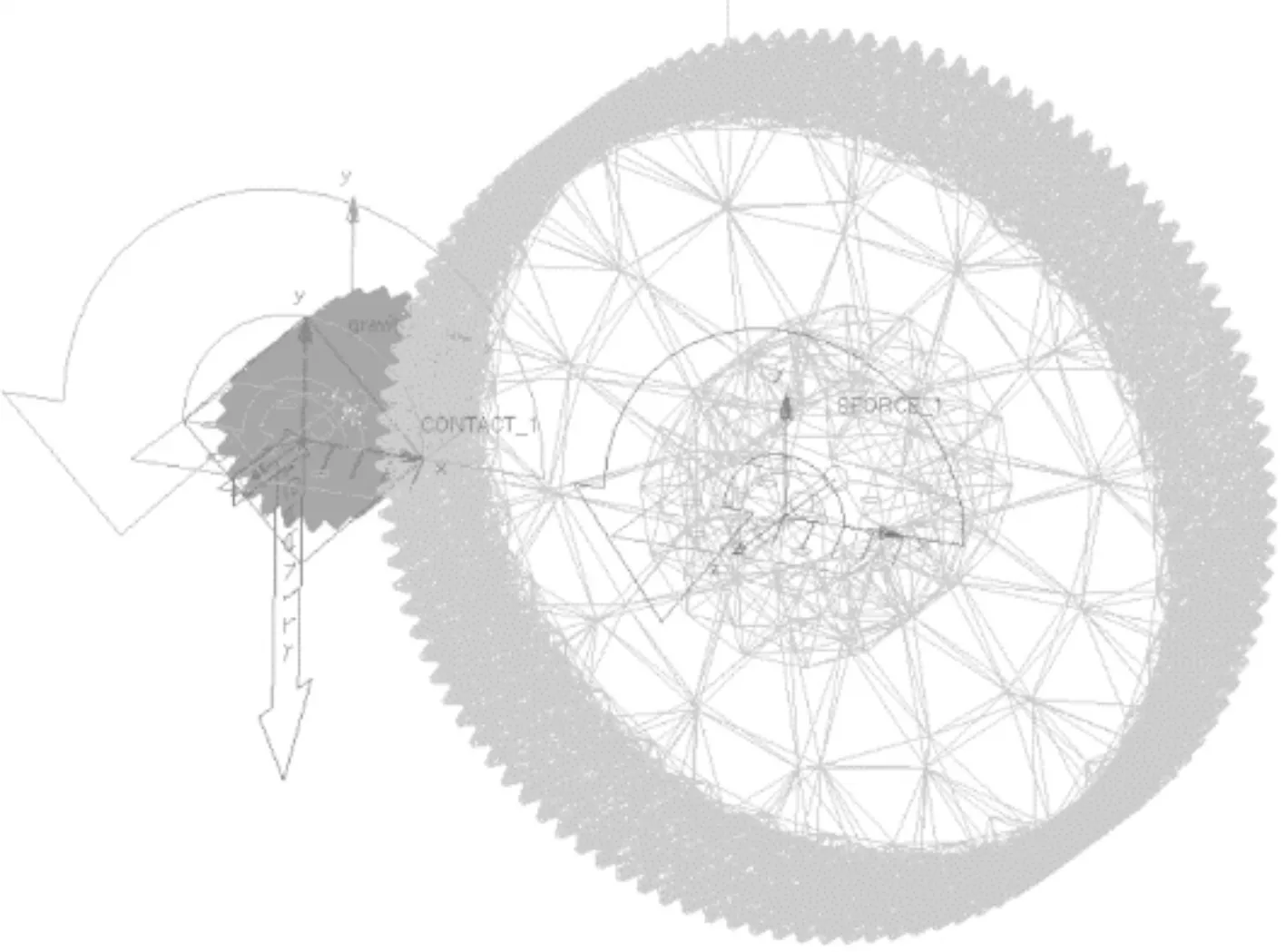
图5 双渐开线齿轮柔性体动力学模型

2.4 动力学模型准确性验证

笔者对刚柔两组动力学模型进行相同的转速及负载设置，同时，为了防止启动时转速的突变，笔者采用STEP渐进函数施加驱动与负载。

STEP函数的表达式如下：

STEP(x,a,h0,b,h1)

(12)

式中：x—自变量。

STEP值域在h0与h1之间，即：

STEP=

(13)

主动轮输入转速为770 r/min(即80.6 rad/s)，负载为从动轮上输出转矩6 000 N·m。

笔者分析所施加的驱动函数表达式具体如下：

驱动：STEP(time,0,0,0.2,80.6)；

负载：STEP(time,0,0,0.2,6 000 000)；

仿真时间为1 s，仿真步数为2 000。

完成参数设置后，笔者运行动力学仿真，测量所设驱动与负载函数，如图6所示。

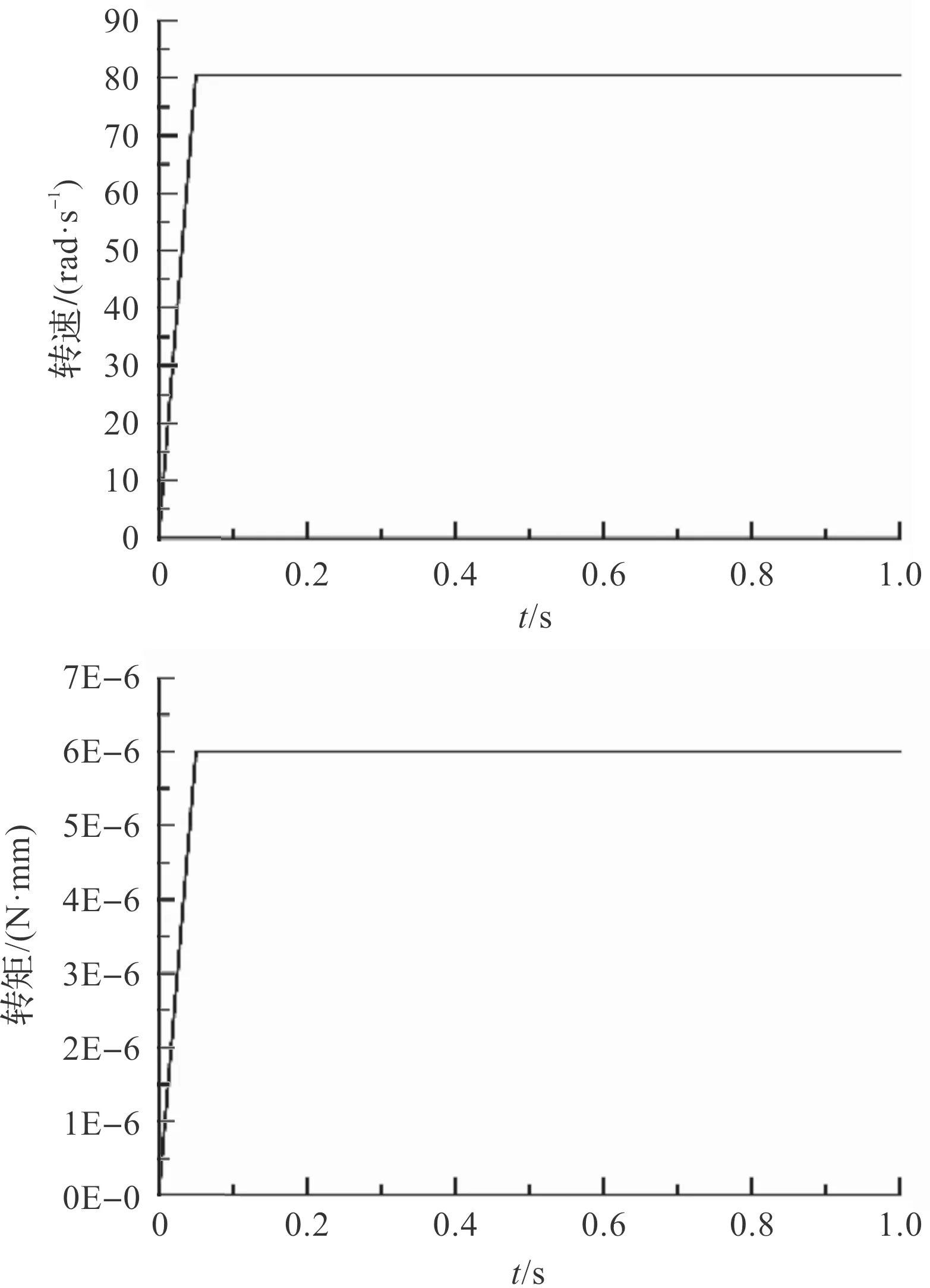
图6 主动轮转速和从动轮转矩示意图

从图6可以看出:在0～0.02 s,主动轮加速到80.6 rad/s后匀速转动,负载转矩也随转速不断增加到6×106N·mm后保持恒定负载,两组动力学模型均设置完成。

3 仿真及结果分析

3.1 齿轮振动角速度及角加速度分析

在对两组模型进行仿真后,在ADAMS中的后处理模块中,可以得到两组齿轮从动轮振动角速度与角加速度的时域图及频谱图。

从动轮振动角速度对比如图7所示。

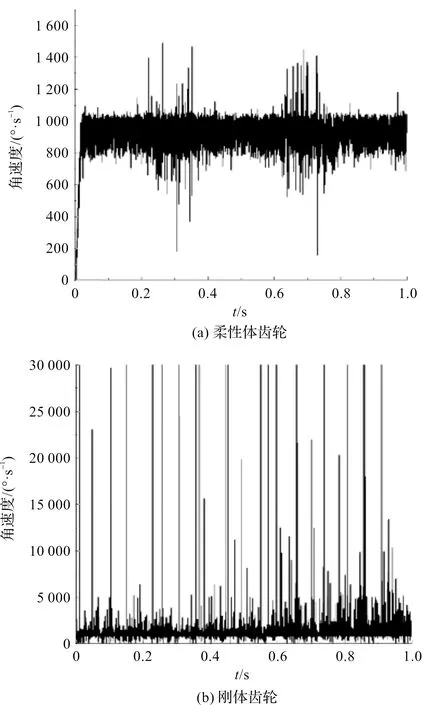
图7 从动轮振动角速度对比

由图7可知:刚体齿轮的振动角速度整体波动大、峰值高,最大值为30 000°/s;柔性体模型振动角速度波动小,加速阶段达到900°/s后在一定范围内波动且有明显的周期性,最大值为1 600°/s,这是因为两种齿轮在传动过程中都会受到负载冲击,产生一个周期性振动波动。

从动轮振动角速度理论与仿真值对比如表3所示。

表3 从动轮振动角速度理论与仿真值对比

由表3可知:从动轮振动角速度理论与仿真值对比,仿真值取平均值计算,可以看出柔性体齿轮的振动角速度误差为0.36%,刚体齿轮误差为56%。

由此可知,柔性体齿轮受到的波动影响较刚体齿轮受到的影响小,振动角速度的峰值小。

从动轮角加速度对比如图8所示。

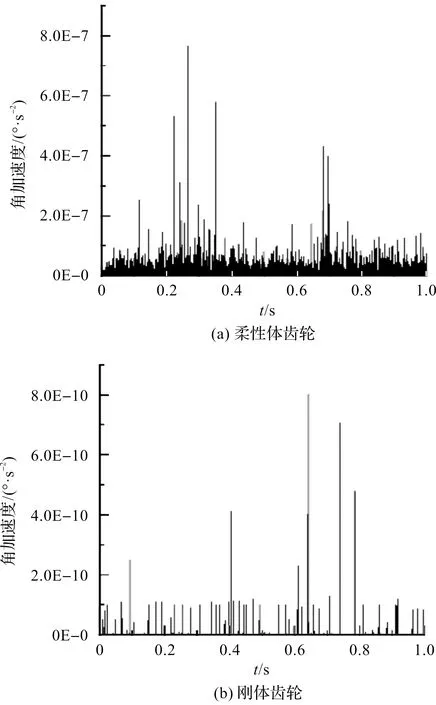
图8 从动轮角加速度对比

由图8可以看出:柔性体齿轮从动轮振动角加速度最大值为8.0×107°·s-2，刚体为8.0×1010°·s-2。刚体与柔性体从动齿轮振动角加速度整体均有波动,柔性体波动小,产生的传动误差小。

由此可知,齿轮柔性化后,减小了齿轮的振动角加速度振幅及传动误差,提高了传动精度及传动平稳性。

3.2 齿轮动态啮合力分析

接下来,笔者通过双渐开线齿轮柔性多体动力学仿真,分析柔性齿轮对齿轮动态啮合力仿真结果的影响。

柔性体与刚体双渐开线齿轮的啮合力时域图如图9所示。

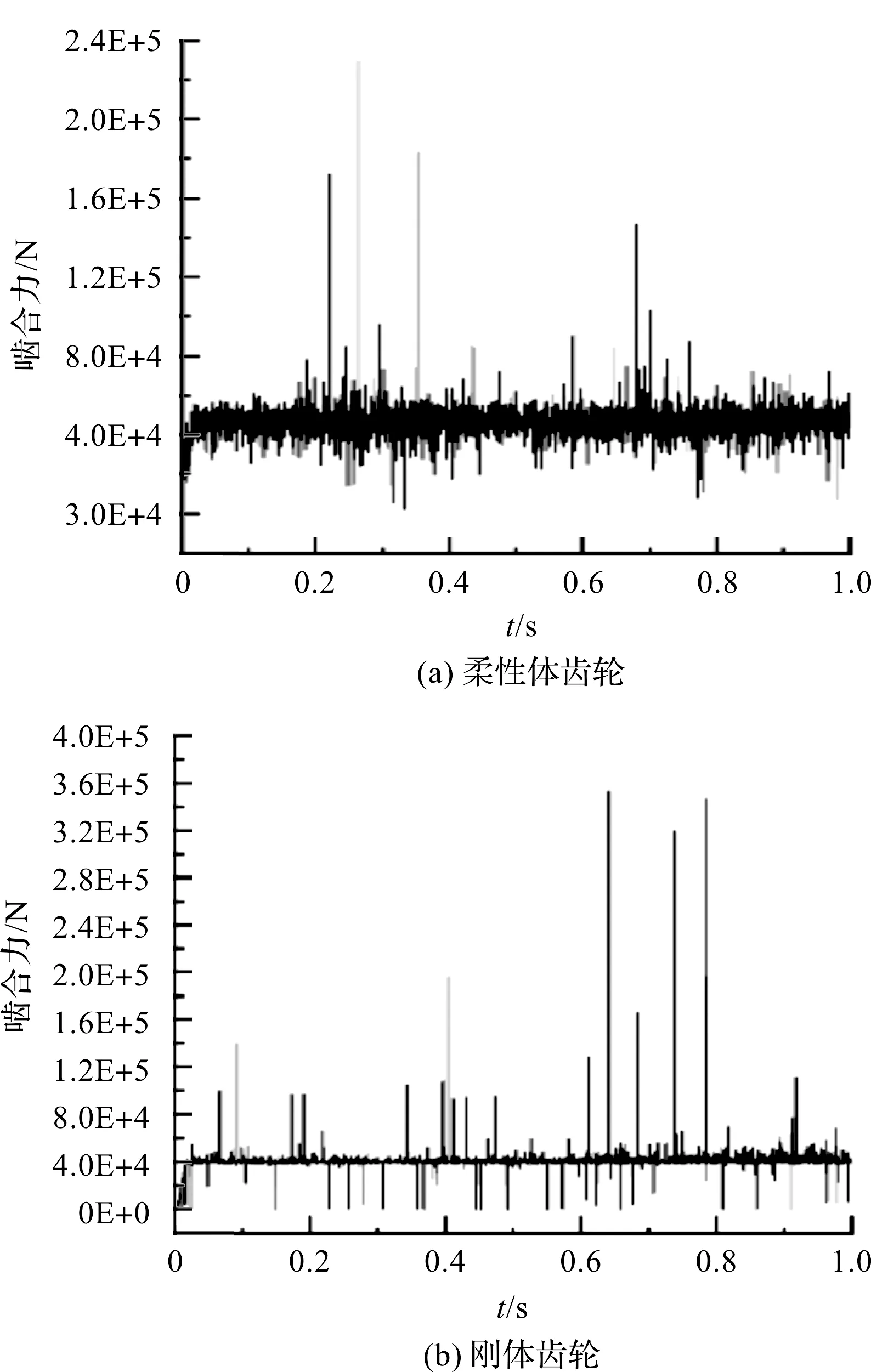
图9 动态啮合力时域图对比

柔性体与刚体双渐开线齿轮的动态啮合力频谱图如图10所示。

在动态啮合力时域图中,取啮合力平均值,经计算可得刚体与柔性体齿轮啮合力的理论值与仿真值的误差均在3%以下,相差不大;但从图中啮合力曲线变化范围可以明显看出:刚体齿轮中啮合力的振幅要比柔性体齿轮大,峰值高,刚体齿轮最大啮合力为4×105N，柔性体齿轮最大啮合力为2.4×105N。

动态啮合力频谱图中,在其各自的基频和倍频处,柔性体齿轮动态啮合力的幅值小于刚体齿轮。由于齿轮系统内部由于啮合接触产生啮合力的变化引起的振动和冲击较大,柔性体接触受力后产生弹性变形,减小了两轮齿的啮合冲击[19，20]。

3.3 齿轮传动变形分析

模态分析是结构动态设计的重要方法,是反映模型变形的重要因素。

考虑到齿轮在实际传动过程中会产生弹性变形及振动[9]203-205,笔者借助ANSYS的模态分析法,分别生成双渐开线与普通渐开线齿轮的柔性体齿轮模型,并选取轮齿上一个marker点,研究齿轮传动过程中,柔性体双渐开线与普通渐开线的角变形量与平移变形量。

角变形量对比如图11所示。

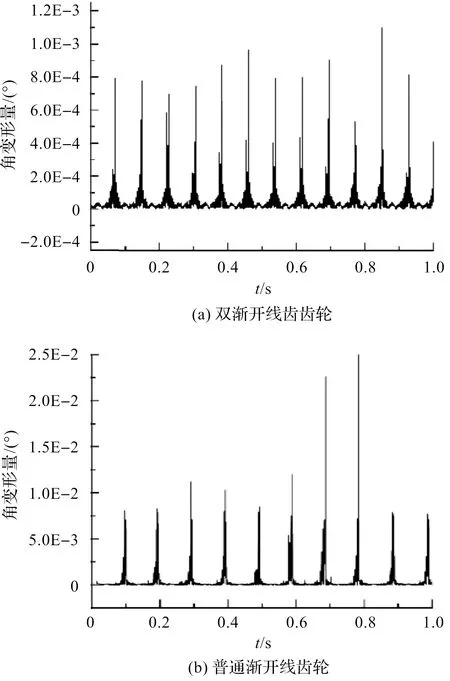
图11 柔性齿轮角变形对比

平移变形量对比如图12所示。

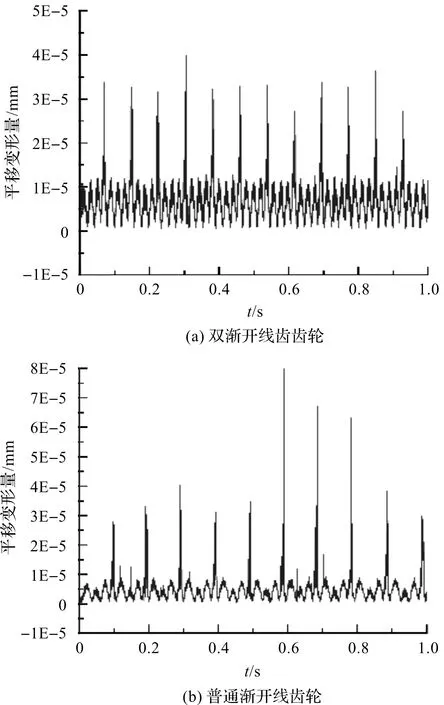
图12 柔性齿轮平移变形对比

根据图(11,12),分析动力学仿真结果可知:

(1)两种齿轮轮齿角变形量与平移变形量随着齿轮啮入、啮出产生较大的峰值并呈周期性变化,未产生塑性变形;

(2)传动过程中,双渐开线齿轮角变形量波动小、振幅稳定,最大角变形量为0.001 1°;普通渐开线齿轮最大角变形量为0.029°,二者均出现在0.8 s附近;

(3)双渐开线齿轮在非啮入、啮出时的平移变形量大于普通渐开线齿轮,但在啮入、啮出时平移变形量小于普通渐开线齿轮[20],普通渐开线齿轮的平移变形量幅值波动大,整体峰值水平更高,最大平移变形量为8.17×10-5mm，双渐开线齿轮最大平移变形量为3.98×10-5mm。

3 结束语

笔者建立了柔性体双渐开线齿轮模型,分析了齿轮的振动角速度、角加速度、齿轮动态啮合力的频幅大小及传动误差,基于模态分析和动力学分析,研究了齿轮传动过程中,柔性体双渐开线齿轮与普通渐开线的角变形和平移变形,得出以下结论:

(1)齿轮柔性化后,在一定程度上有助于减小从动轮的振动角速度及角加速度,降低了齿轮传动过程中的振动波动;

(2)齿轮柔性化后,降低了齿轮在其基频及倍频处的峰值,对齿轮啮入与啮出时的载荷冲击有一定缓冲作用,保证了齿轮运动的平稳性;

(3)齿轮柔性化后,双渐开线齿轮与普通渐开线齿轮的变形量均呈周期性变化,双渐开线齿轮的传动角变形量与平移变形量在其啮入与啮出时整体波动小,相对稳定且均小于普通渐开线齿轮。

笔者在后续的研究方向为:(1)在柔性多体动力学的基础上,进一步研究不同工况下,双渐开线齿轮和普通渐开线齿轮的点蚀、安装中心距误差等的动力学特性;(2)进行基于柔性多体动力学的双渐开线齿轮温度场研究。