基于ADAMS的双渐开线齿轮动态性能研究

樊智敏，江 峰，陈 亮

(青岛科技大学机电工程学院，山东 青岛 266061)

齿轮作为一种传递动力和运动的装置，被广泛应用于航空航天、汽车、船舶等各个领域，而齿轮的检测与制造又是衡量一个国家工业水平的标准，深入探究双渐开线齿轮的动态性能具有重要意义。邹玉静等[1]综合考虑时变啮合刚度、齿面摩擦等因素对齿轮动力学特性的影响，基于摩擦学与动力学之间的耦合关系，分析了转速、载荷对渐开线斜齿轮的动态响应。程言丽等[2]基于理论分析、ADAMS动态仿真、实验测试3种方法研究了渐开线直齿轮的动态特性，并将3种结果进行对比，验证了动态仿真方法与实验结果的准确性。Sun等[3]建立了行星齿轮振动分析模型，研究了转速波动对齿轮啮合周期振动的影响。Ouyang等[4]通过理论建模和实验测试分析了不同工况下齿轮-滚珠轴承系统在时、频域的振动信号，验证了数学模型预测振动响应的有效性。Yua[5]基于ADAMS建立行星齿轮虚拟样机，分析了不同载荷下行星齿轮的动态性能。Wang等[6]综合考虑齿轮的刚度激励和冲击激励，提出一种改进的GTF齿轮箱动力学模型，分别在时域、频域两个方面与原模型对比，论证了改进模型的动态特性。Feng等[7]提出一种考虑磨损的齿轮振动预测方案，分析了齿面磨损对齿轮箱的振动响应。 Khabou等[8]研究了变工况下直齿圆柱齿轮系统的瞬态特性以及齿轮减速器在不同转速下的动态响应。Cao等[9]建立了直齿轮动力学模型，研究了齿轮的非线性频率响应特性。王明凯等[10]建立了双渐开线齿轮摩擦动力学模型，研究了转速对齿面摩擦状态的影响以及不同摩擦因数下双渐开线齿轮动力学行为。

双渐开线齿轮作为一种新型齿轮，考虑其动态接触特性的研究仍处于薄弱环节，且其与普通渐开线齿轮的动态性能好坏也尚不明确，本文基于ADAMS建立双渐开线齿轮虚拟样机，对比分析了同参数、同工况下普通渐开线齿轮与双渐开线齿轮的动态性能，研究了齿腰分阶参数对双渐开线齿轮齿面法向接触力的影响，为后续深入研究双渐开线齿轮动力学特性奠定了基础。

1 双渐开线齿轮

双渐开线齿轮是一种综合双圆弧齿轮和渐开线斜齿轮优点的新型齿轮，其齿廓由两段相错渐开线组成，两段渐开线中间以一段圆弧过渡曲线连接，齿顶渐开线与齿根渐开线呈分阶式布置[11]。双渐开线基本齿廓如图1所示，实线表示双渐开线齿轮基本齿廓，虚线表示普通渐开线齿轮基本齿廓。其中齿根渐开线BC与齿根过渡圆弧曲线AB在B点相切，与齿腰过渡圆弧曲线CD相交于C点，齿顶渐开线DE与齿腰过渡圆弧曲线CD在D点相切。 由于双渐开线齿轮在节点附近分阶，其节点前后不参与啮合，与普通渐开线齿轮相比，双渐开线齿轮齿根增厚，齿顶变薄。

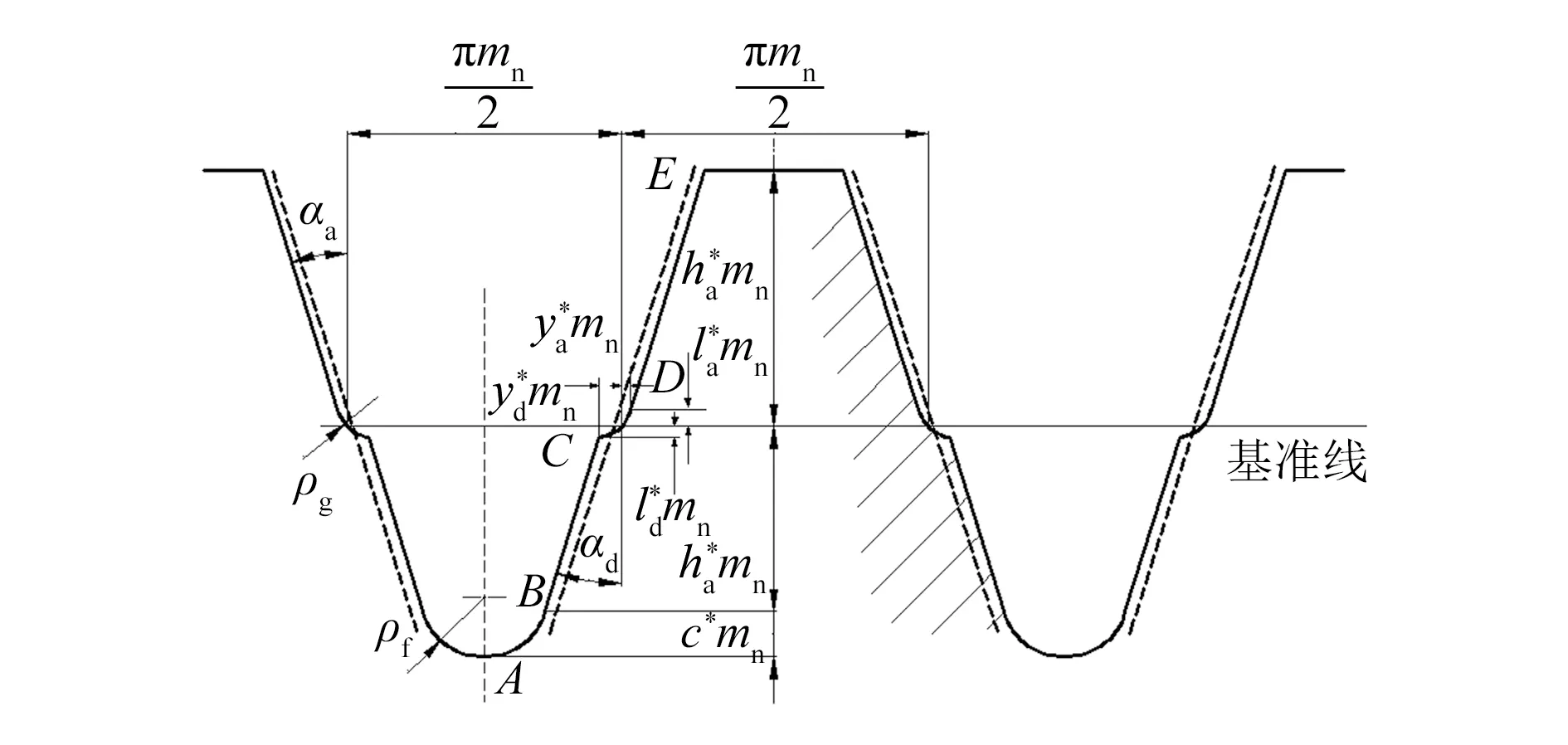
图1 双渐开线齿轮基本齿廓

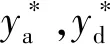
2 虚拟样机的建立

目前大多数研究者在对齿轮仿真时将齿轮模型默认为“刚体”进行研究，结果与实际存在较大误差。本文综合考虑双渐开线齿轮的弹性变形以及其非线性动力学特性，对齿轮模型进行柔性化处理，建立柔性体双渐开线齿轮虚拟样机。

操作流程为：

1)根据表1双渐开线齿轮齿廓参数和材料属性，建立双渐开线齿轮三维模型。

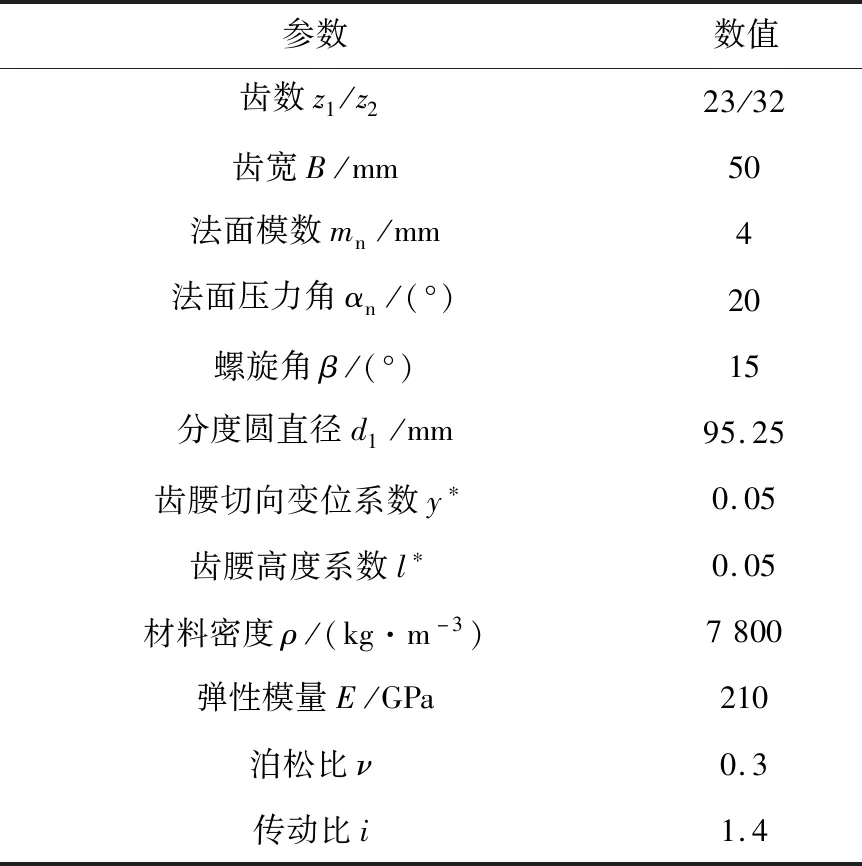
表1 齿廓参数和材料属性

2)将双渐开线齿轮三维模型导入ANSYS中进行模态分析，分析结果保存为MNF模态中性文件。

3)将MNF文件导入ADAMS中建立柔性体齿轮虚拟样机，如图2所示。

图2 双渐开线齿轮虚拟样机

3 接触力算法

3.1 基于ADAMS的法向接触力算法

为准确模拟齿轮实时啮合状态，对建立的虚拟样机添加碰撞接触。ADAMS中碰撞函数(Impact)是将轮齿的啮合接触等效为具有渗透深度的非线性弹簧-阻尼模型，齿轮法向接触力Fn的大小与齿轮的接触刚度和轮齿渗透量有关，表达式为[12]：

(1)

式中：K为接触刚度；δ为啮合点处法向变形量；n为碰撞指数；δmax为最大法向变形量；Cmax为最大接触阻尼：t为发生变形的时间；step为阶跃函数。

其中接触刚度K表征齿轮受力时抵抗变形的能力，表达式为：

(2)

(3)

(4)

式中：R为综合曲率半径；R1,R2为主、从动轮啮合点处曲率半径；ν1,ν2为主、从动轮材料的泊松比；E为综合弹性模量；E1,E2为主、从动轮材料的弹性模量。

本文所用齿轮材料为45钢，材料参数为：泊松比ν1=ν2=0.3；弹性模量E1=E2=210 GPa；碰撞指数n的数值一般为1.3～1.5，本文设为1.5；设最大阻尼击穿深度为0.1 mm；齿轮设计参数R1=47.623 mm，R2=66.258 mm。

3.2 接触力的理论计算

齿轮法向接触力可分解为周向、轴向、径向3个方向的接触力[13]。

周向接触力Ft：

(5)

式中：T1为主动轮传递转矩；d1为主动轮分度圆直径。

轴向接触力Fa：

Fa=Fttanβ

(6)

径向接触力Fr：

(7)

3.3 啮合激振频率

齿轮啮合激振频率f表达式为：

(8)

式中：n1为小齿轮转速。

4 动力学仿真及分析

4.1 虚拟样机的验证

通过对齿轮虚拟样机定义接触、设置接触碰撞参数、选择动力学方程求解算法以及施加驱动、负载等工况，完成齿轮动力学仿真的前处理。

对双渐开线齿轮主动轮施加转速1 500 r/min(9 000(°)/s)，从动轮施加转矩100 N·m，进行动力学仿真验证。为避免施加转速过高造成瞬时冲击，对齿轮虚拟样机添加step阶跃函数命令，使主动轮转速在0.2 s内逐步过渡到1 500 r/min，主、从动轮转速如图3所示。

由图3(a)可知，在0—0.2 s内双渐开线齿轮处于增速阶段，转速波动较大，0.2 s后主动轮转速恒定。由图3(b)可知，当主动轮转速恒定时，从动轮转速在一定范围内上下波动，波动原因是轮齿啮合过程中会产生啮合冲击等周期性激励，从而引起齿轮传动比波动。由表1中传动比可知，虚拟样机的部分仿真结果与理论计算值存在良好的一致性，说明建立柔性体双渐开线齿轮在一定程度上能反映齿轮的实际工况。

4.2 转速对比分析

由图3可知，传动比波动会引起齿轮转速波动，本文将双渐开线齿轮与同参数、同工况的普通渐开线齿轮转速波动进行对比，对比结果如图4所示。

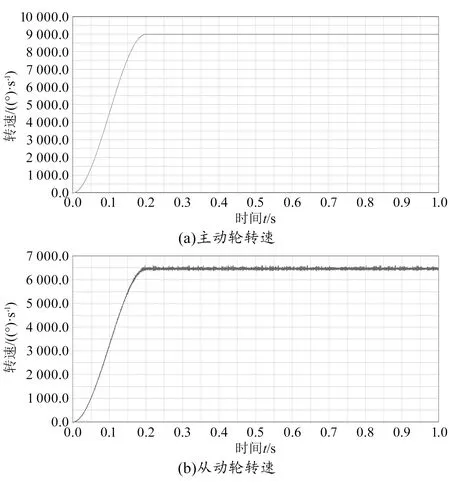
图3 双渐开线齿轮主、从动轮转速

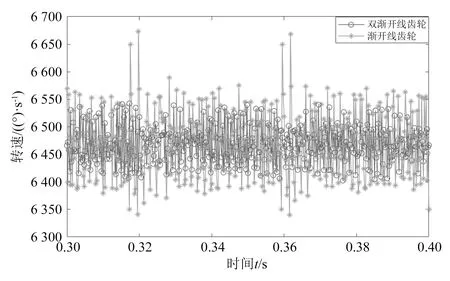
图4 转速波动对比分析

由图4可知，双渐开线齿轮与普通渐开线齿轮的转速均呈现出不规则的周期性波动，双渐开线齿轮的转速波动幅值明显小于同参数的普通渐开线齿轮，其转速波动较为平稳，普通渐开线齿轮存在转速瞬时增大现象，在一定程度上说明了双渐开线齿轮相较于普通渐开线齿轮传动更平稳。

4.3 齿面接触力分析

为进一步研究双渐开线齿轮的动态性能，将同参数、同工况(主动轮转速1 500 r/min、从动轮转矩100 N·m)下双渐开线齿轮与普通渐开线齿轮法向接触力进行对比分析，分析结果如图5所示。

由图5(a)、(b)可知，双渐开线齿轮与普通渐开线齿轮法向接触力均围绕某一定值上下波动，双渐开线齿轮法向接触力幅值变化较为平稳，普通渐开线齿轮接触力存在瞬时突变，这是由于齿轮瞬时啮合冲击造成的，普通渐开线齿轮法向接触力的波动幅值和最大值均明显高于双渐开线齿轮。通过对齿轮时域图进行傅里叶变换可得出齿轮的频谱图，由图5(c)、(d)可知，双渐开线齿轮与普通渐开线齿轮法向接触力的峰值均出现在理论计算激振频率的基频、二倍频、三倍频处，但变化规律不同，普通渐开线齿轮最大峰值(273.62 N)位于基频处，而双渐开线齿轮最大峰值(154.57 N)位于二倍频处，基频对双渐开线齿轮影响较小。双渐开线齿轮法向接触力最大峰值小于普通渐开线齿轮，在基频、二倍频、三倍频处普通渐开线齿轮波动峰数显著多于双渐开线齿轮，由此可知激振频率响应下双渐开线齿轮的振动冲击会低于普通渐开线齿轮。

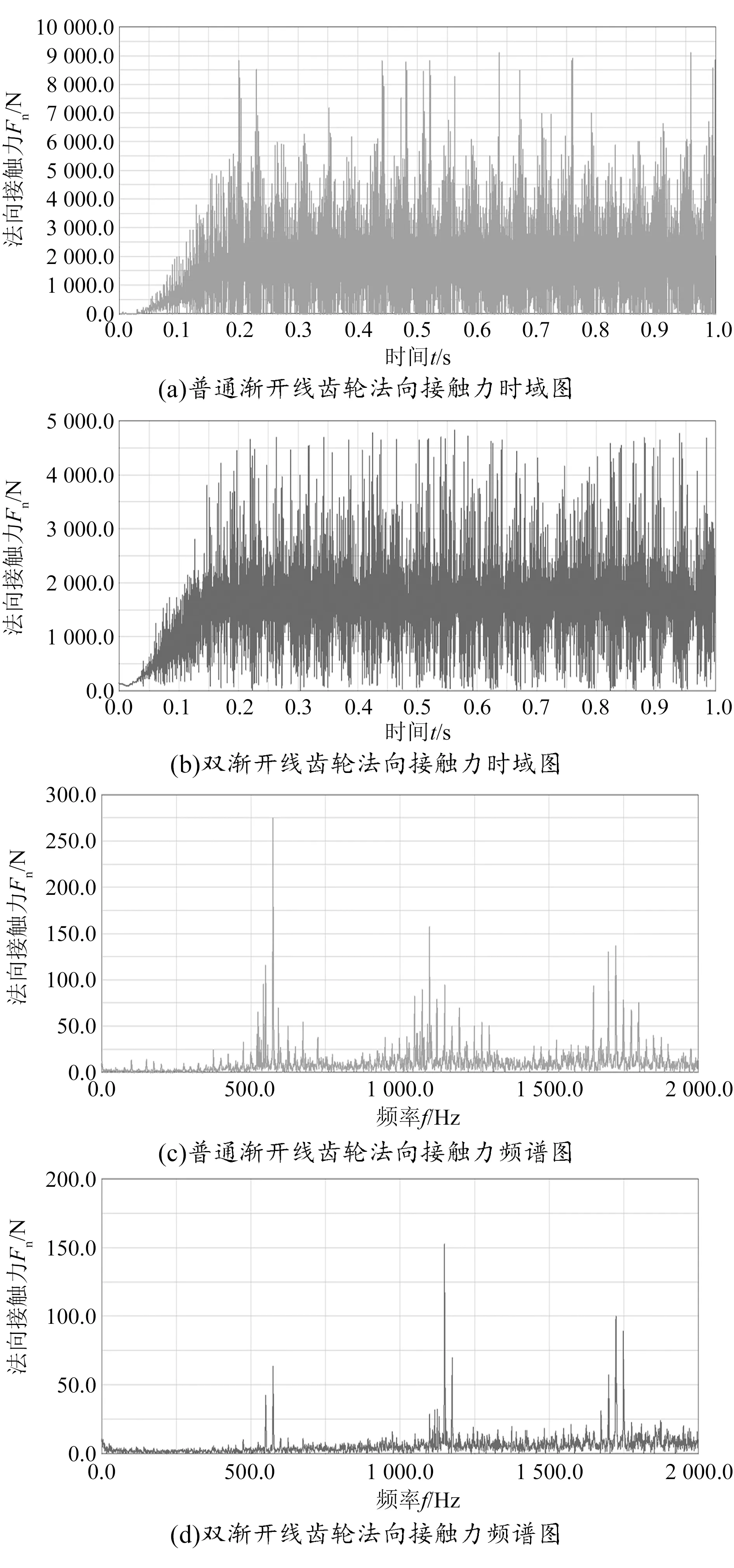
图5 法向接触力对比分析

为进一步研究双渐开线齿轮与普通渐开线齿轮在径向、轴向、周向的振动冲击情况，将双渐开线齿轮与普通渐开线齿轮3个方向的接触力进行对比分析，分析结果如图6所示。

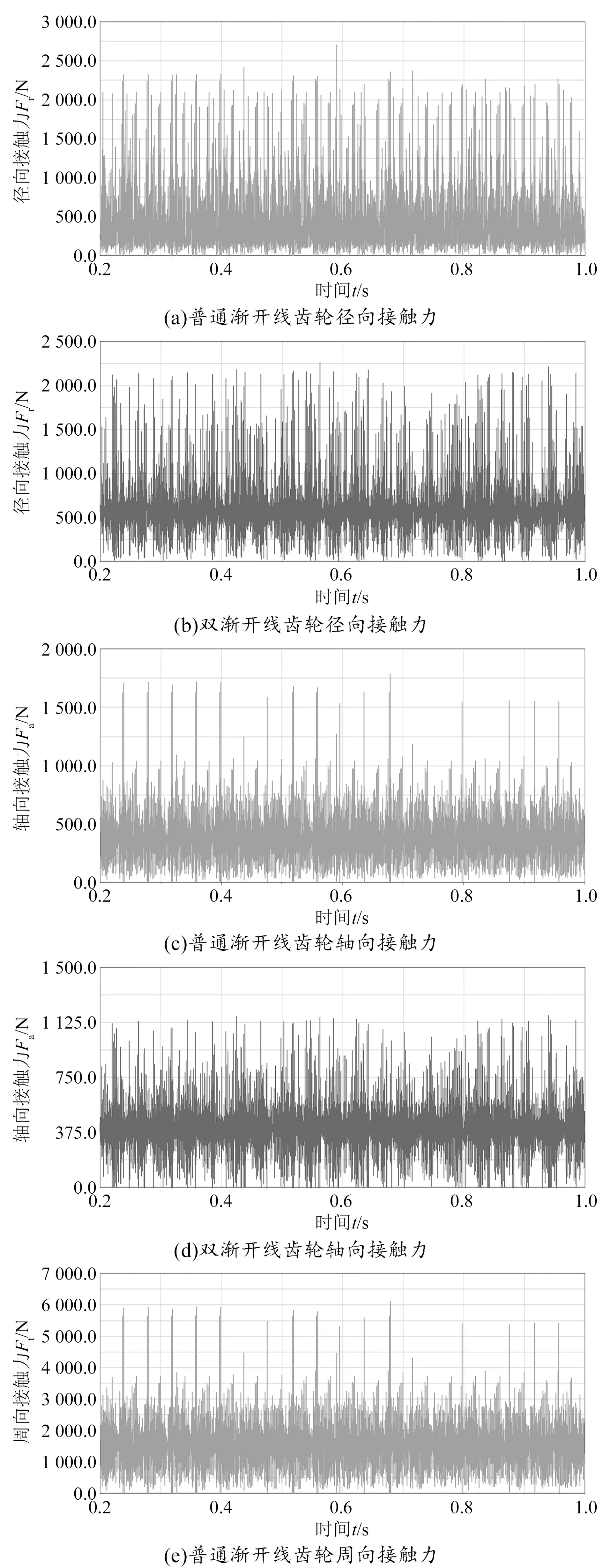
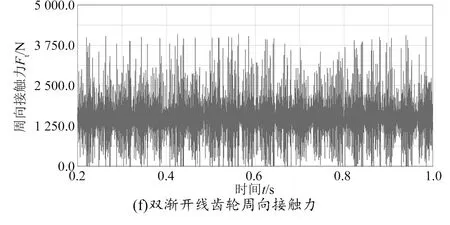
图6 径向、轴向、周向接触力对比分析

由图6(a)、(b)可知，双渐开线齿轮与普通渐开线齿轮径向接触力的变化规律存在一定差异，但二者的波动幅值和最大值相差不大。由图6(c)、(d)、(e)、(f)可知，双渐开线齿轮的接触力波动相对平稳，普通渐开线齿轮轴向、周向接触力存在明显的周期性瞬时突变，普通渐开线齿轮的轴向、周向接触力波动幅值和最大值均显著大于双渐开线齿轮，说明在传动过程中普通渐开线齿轮的轴向、周向冲击振动大于双渐开线齿轮，而长时间的冲击振动会对齿轮产生一定损伤，周期性的损伤积累更容易造成疲劳接触失效，由此可知，双渐开线齿轮的动力学特性在某种程度上要优于同参数的普通渐开线齿轮。

将双渐开线齿轮与普通渐开线齿轮径向、轴向、周向、法向接触力的动态仿真均值设为仿真值，并与理论值进行对比，发现接触力误差均在10%以内，验证了仿真结果的准确性，对比结果见表2。

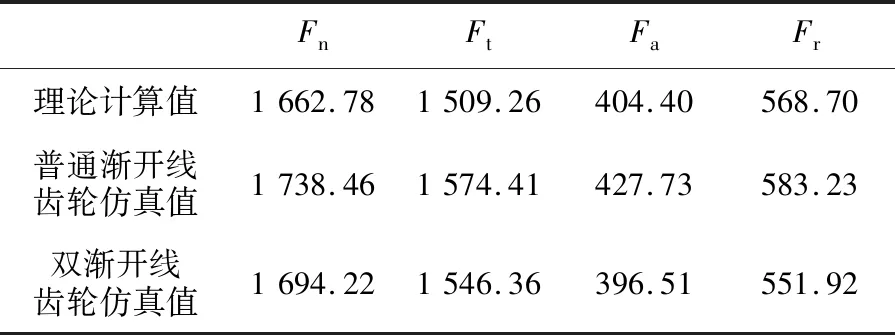
表2 接触力理论值与仿真值对比分析 单位：N

由上述分析可知，双渐开线齿轮与普通渐开线齿轮存在一定共性，对普通渐开线齿轮齿腰分阶，能在某种程度上改善普通渐开线齿轮的动力学特性。

4.4 齿腰分阶参数对法向接触力的影响

齿腰分阶参数是双渐开线齿轮区别于普通渐开线齿轮的重要特征参数，探究齿腰分阶参数对双渐开线齿轮动态性能的影响，不仅能得到齿面法向接触力的变化规律，还能明确齿腰分阶参数对改善齿轮动力学性能的重要性。

图7为齿腰高度系数l*=0.05时，双渐开线齿轮法向接触力随齿腰切向变位系数y*的变化情况。

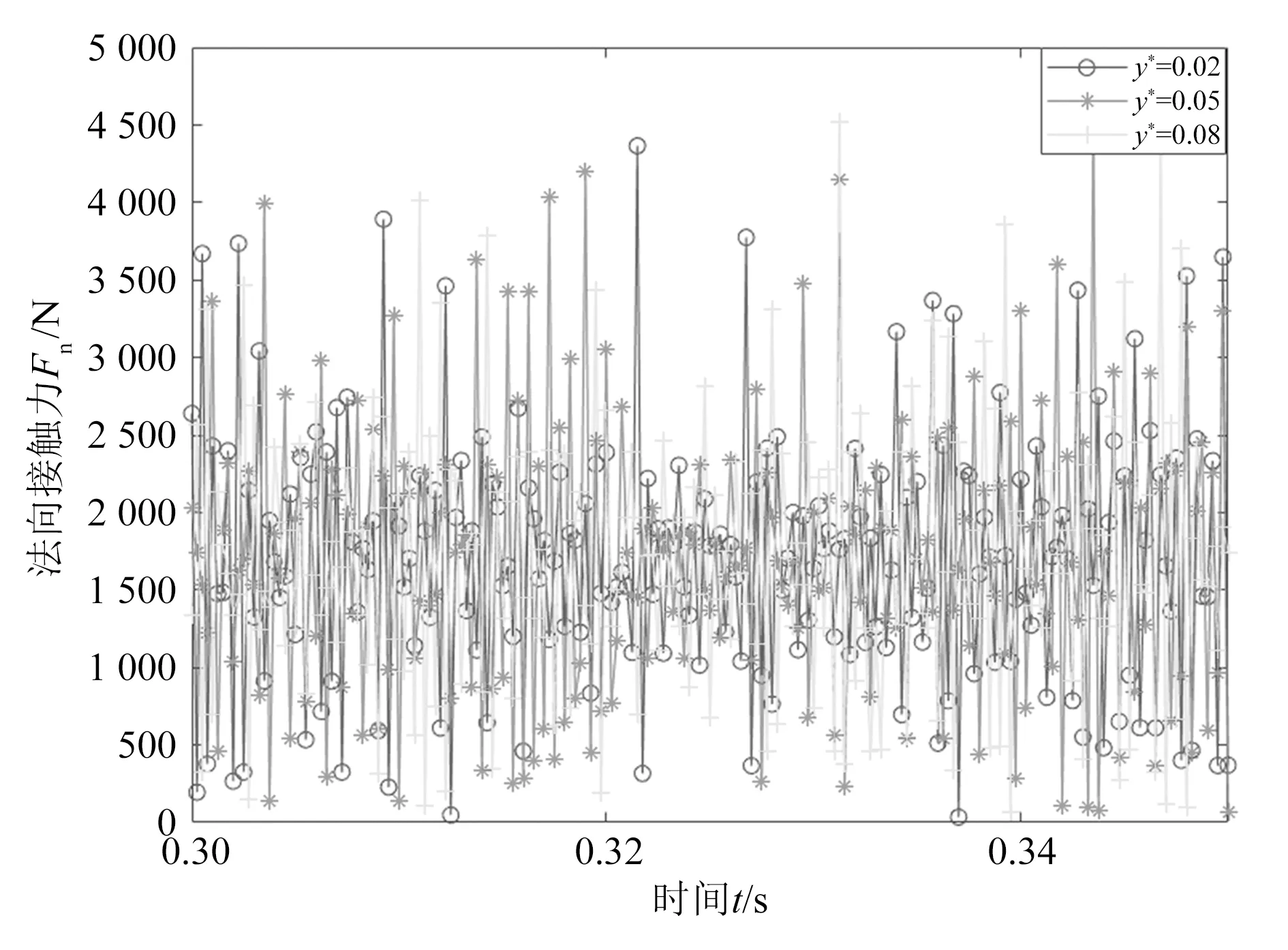
图7 切向变位系数对法向接触力的影响

由图7可知，改变切向变位系数会对双渐开线齿轮法向接触力变化规律产生一定影响，但影响较小，不同切向变位系数下法向接触力波动幅值相差不大，法向接触力最大值随切向变位系数的增大略微增大，这是由于切向变位系数y*对双渐开线齿轮齿面接触线长度影响较小，对齿轮受力影响不大。

图8为齿腰切向变位系数y*=0.05时，双渐开线齿轮法向接触力随齿腰高度系数l*的变化情况。

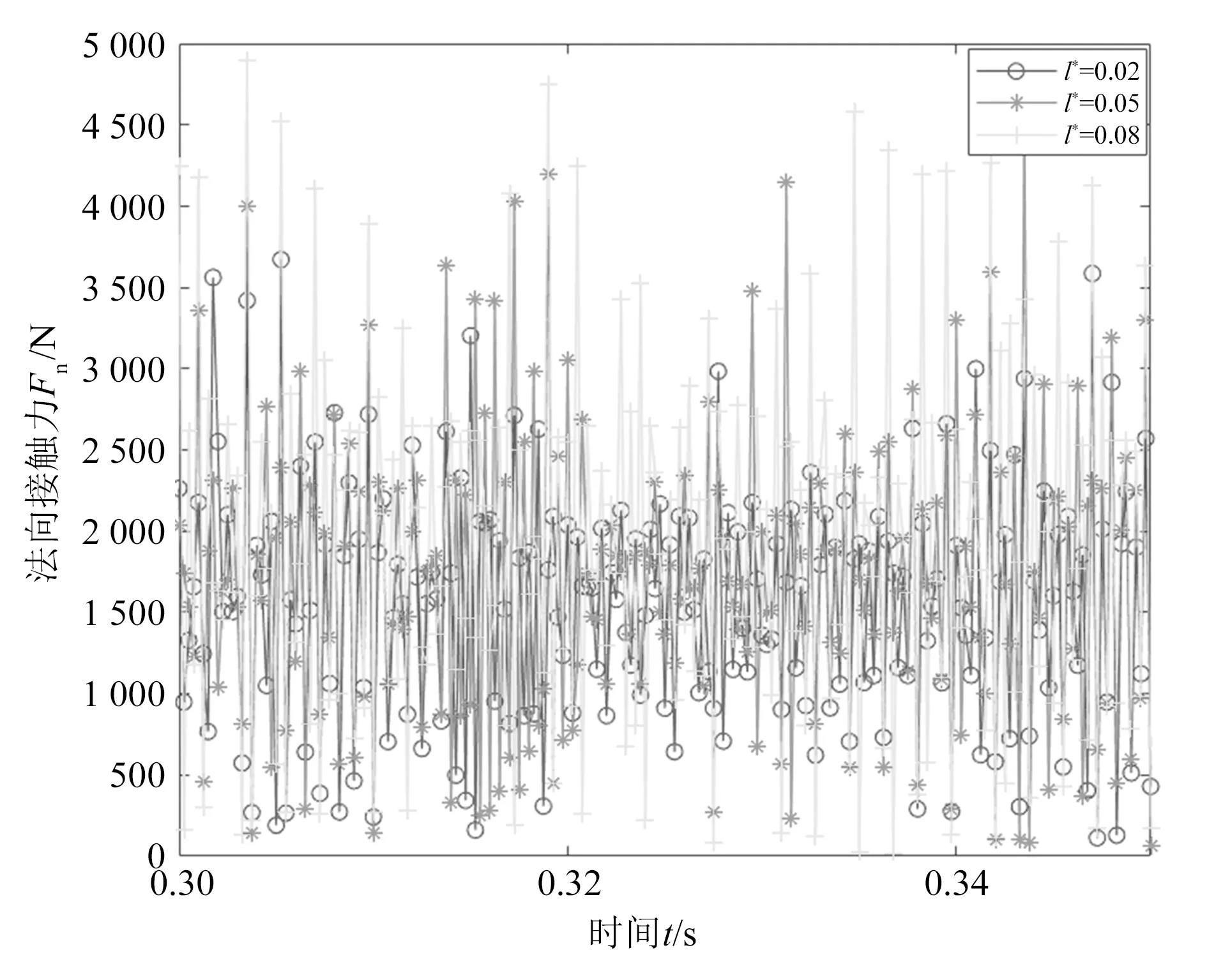
图8 齿腰高度系数对法向接触力的影响

由图8可知，齿腰高度系数对双渐开线齿轮齿面法向接触力变化规律影响较大，法向接触力的波动幅值和最大值均随齿腰高度系数l*的增大而增大，这是由于l*增大，导致双渐开线齿轮齿面损失重合度增大、接触线长度变短、单位线载荷增大造成的。通过对比发现，齿腰高度系数对双渐开线齿轮动态性能的影响明显大于切向变位系数。因此双渐开线齿轮在设计时应合理选择齿腰高度系数，避免不良现象发生的同时，还为进一步改善双渐开线齿轮的动力学性能提供了依据。

5 结论

本文通过对双渐开线齿轮的动态性能研究，得出以下结论：

1)同参数、同工况下双渐开线齿轮的转速、法向接触力的波动幅值和最大值均小于普通渐开线齿轮，激振频率附近双渐开线齿轮法向接触力最大峰值小于渐开线齿轮。

2)双渐开线齿轮的轴向、周向振动冲击小于同参数的普通渐开线齿轮。

3)双渐开线齿轮的动态性能和稳定性在一定程度上优于同参数、同工况的普通渐开线齿轮。

4)齿腰高度系数对双渐开线齿轮动态性能的影响大于齿腰切向变位系数，通过合理选择齿腰分阶参数能改善双渐开线齿轮的动态性能。