基于随机矩阵的PMU装置暂态脱机检测误差修正

马恩宁

(云南大理供电局变电修试所，云南 大理 671000)

为增强电力调度系统动态监测与分析的能力，电力公司采取在重点变电站或发电厂中安装同步向量测量装置(phase measurement unit，PMU)的方法，构建自身的实时动态监测系统，以便电力工作人员能够实时了解电力系统运行状态[1-2]。PMU是监测系统的核心，因此其必须具备高精度、低误差的计算和数据处理能力。PMU的测量可以分为幅值测量和相位角测量，PMU测量过程中会受到自身算法的影响而产生误差，从而导致分析结果出现错误，最终影响电力系统的整体运行效果[3-4]。

计算机的发展促进了算法的应用，在提升计算速度的同时也促进了电力系统的深层发展。其中随机矩阵与传统的数据算法相比，在检测微弱目标方面具有更好的性能，随机矩阵能够利用各个监测点噪声的独立同分布特点，实现多个PMU处理接收到的单一信号，完成对电力系统中弱信号的检测。因此，本文提出基于随机矩阵的PMU暂态脱机检测误差修正方法，用于检测弱目标信号，提高电力系统的运行效率。

1 检测误差修正

1.1 建立数学模型

由于一些客观因素的限制，PMU一般应用在主网中，但是电力系统分支数量多、结构复杂，因此低成本、大数量的PMU才能够满足配电网运行的需求[5]。用印刷线路板(printed circuit board,PCB)罗氏线圈来降低成本的PMU装置的结构如图1所示。

在配电网中，当某一信号的电压电流值能够被直接测量或间接计算出来，那么该信号即为可观测信号[6-7]，信号的可观函数Fj的表达式为：

Fj=ki-w2mi

(1)

式中：ki为信号的观测模态；w为电流观测影响指数；mi为电压观测影响指数。

将PMU配置在电力系统中，能够计算出对应信号点的幅值f与相位角θ，计算公式分别为：

f=Pxv·Fj

(2)

θ=fsin[2π(t/T+W)]

(3)

式中：Px为信号点的脉冲位移；v为信号点的波动参数；t为任意时刻；T为采样时间间隔；W为信号点的相位。

在没有条件限制的情况下，为了保证配电网的可靠性，需要对PMU进行配置优化，采用0-1整数规划法建立配置优化的数学模型[8]。0-1是整数规划的特殊情况，其决策变量仅有0-1变量，则构建配置优化的数学模型Qi为：

(4)

式中：cj为信号j上PMU的安装费用；I为电力控制信号；uj为PMU配置成本；aij为i，j信号的关联函数。对于PMU配置数学模型，本文采用割平面法进行求解，即在不考虑整数约束条件的情况下求出约束条件松弛的最优解χ：

(5)

式中：n为信号频率；η为最优约束参数。

当该解为非整数时，需要增加能去除非整数解的线性约束条件，保留整数可行域过程中得到的整数解，最终得到被切割多次后保留下来的全部整数解[9]。至此完成PMU配置数学模型的构建与分析。

1.2 误差修正

当建立的PMU数学模型经过优化配置后，能够在保证电力系统全局可观的同时[10-11]，保证PMU在暂态脱机状态下不会忽略弱信号的感知，可有效完成检测误差的修正。利用随机矩阵来处理PMU的实时数据，能够实现信号矩阵重构，增强弱信号强度。重构后的信号矩阵xti为：

(6)

式中：xnM为第n行第M列的元素。

设Xn=(xij)m×n是一个复随机矩阵，其中xij是独立随机变量并满足期望为0、方差为1的标准正态分布，随机矩阵的构建示意图如图2所示。

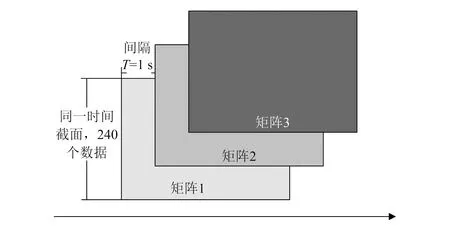
图2 随机矩阵构建示意图

在修正过程中，利用随机矩阵能够有效避免重复修正的情况。得到最新时间截面数据生成随机矩阵后，需要选择分析方法对其进行分析[12-14]，记录与每个最新的随机矩阵相应的统计量。

假设在电力系统中有n个接收端，每个PMU所探测的信号维度为M，那么在任意时刻t，所接收的信号可以构成二维矩阵：

(7)

在T个采样时间间隔下，在原始的数据矩阵中，只考虑M为2的情况，将上述矩阵的行向量进行标准化处理，得到误差修正表达式：

(8)

本文选用最大、最小特征值法对随机矩阵进行分析，该方法基于随机矩阵理论，通过多个PMU对接收到的信号进行处理，分别计算出最大最小特征值：

(9)

(10)

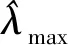
(11)

当修正后的误差大于允许范围时，比值大于1，则需要重新进行修正，直至修正后的误差在规定范围内。

采集到数据后，需要对k进行归一化处理，从而消除奇异样本数据导致的不良影响，以提高误差修正的精度。通过判断比值确定误差情况，直至修正后的误差在规定范围，完成误差修正。

2 实验

2.1 实验准备

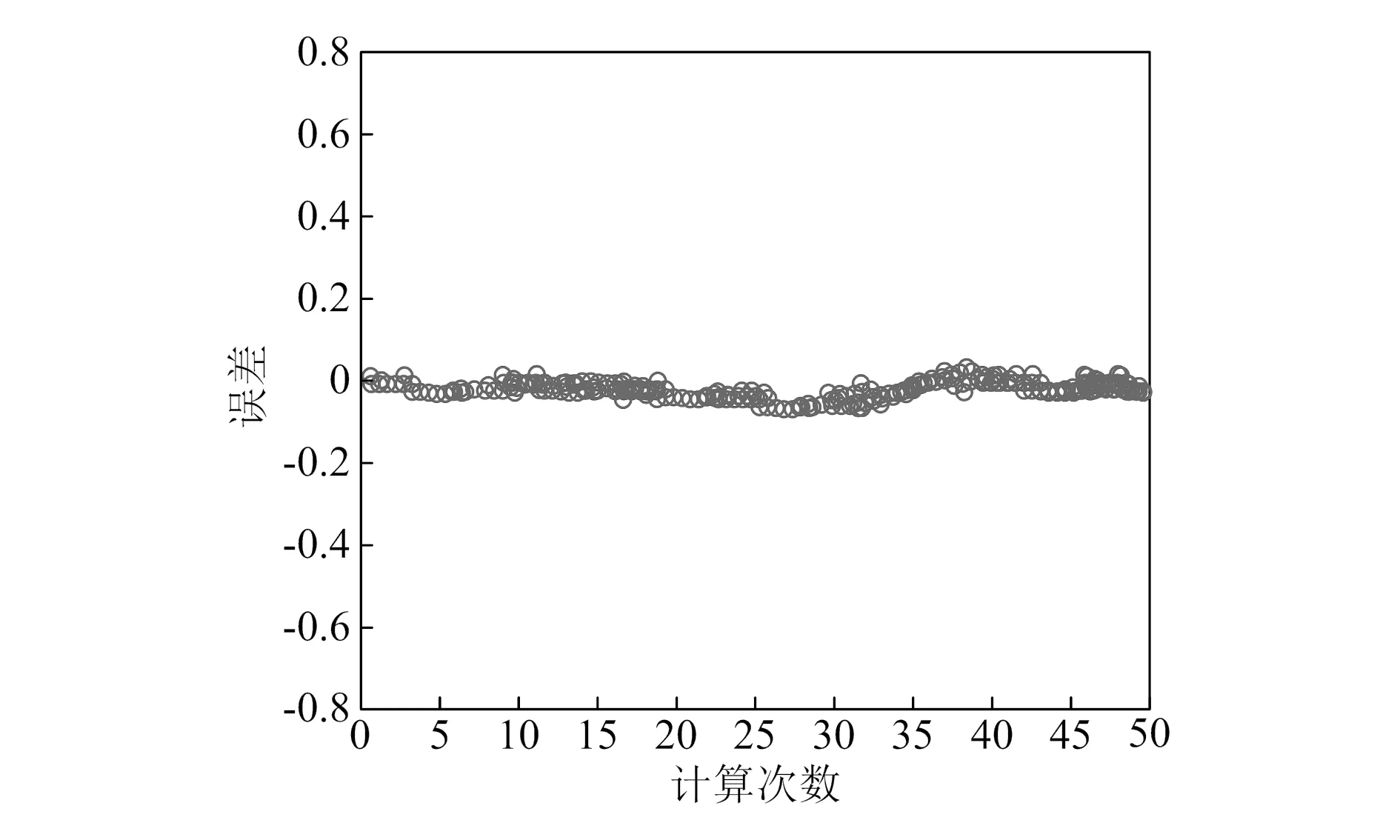
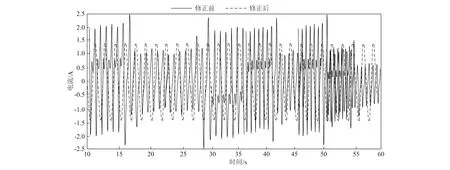
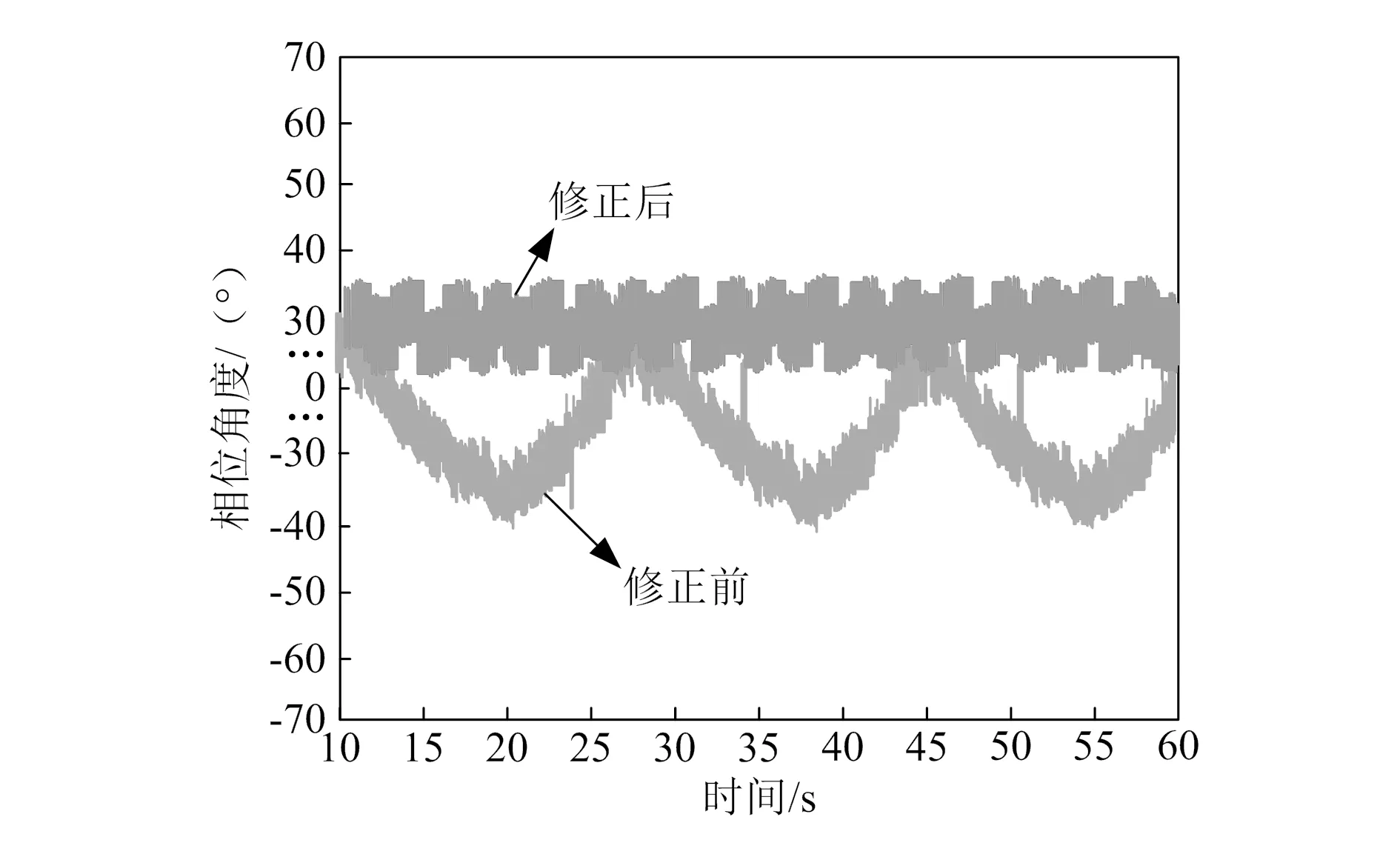
将本文所构建的矩阵模型应用到仿真的电力系统中，共有80个PMU同时进行三相电路的采样，其中每0.000 5 s为一个采样周期，采样时长共2.0 s，那么在同一个时间截面下，一共有240个数据，总计4 000×240个采样数据。选取滑动窗口的方式构建PMU采样信号的随机矩阵时，通常要求M×n维矩阵中M

为了验证本文所提的误差修正方法是否有效，需要设计测试实验进行验证。在调试PMU的过程中，需要用到数字万用表、示波器、Keil μVision4、串口调试助手、网络调试助手、J-Link仿真器等工具。实验室测试的主要目的是验证本文所提的误差修正方法的有效性，看修正后的检测精度是否达到要求。测试过程中主要使用RD-33便携式三相标准表，其综合误差为0.01%，配合BD-3D型多功能校验仪，综合误差为0.05%。将校验仪产生的三相交流电压、电流信号接入标准表和PMU暂态脱机监测的输入端，利用标准表测出的标准值，将各相电参量进行系数调标，完成调试后，采用6100A多功能三相标准功率源对本文方法的电压幅值、电流幅值以及电流电压间相位角等参量进行检测，以最后得到的结果作为参考来验证PMU的检测精度。测试平台如图3所示。

图3 实验测试平台

2.2 约束条件求解

约束条件最优解直接影响对数学模型的求解结果，因此需要对约束条件的求解误差进行验证，在50次实验条件下，本文所提方法的约束条件求解结果如图4所示。

图4 约束条件求解结果

分析图4可知，在多次计算中本文所提方法的约束条件最优解计算误差均在0附近小幅度波动，最大误差不超过0.1。由此说明本文所提方法能够准确求解数学模型，为有效的误差修正奠定基础。

2.3 误差修正

1)电压误差修正。

在三相电压幅值测试过程中，设置6100A多功能标准源的输出频率为50 Hz，标准电压信号为220 V，经过测试，得到的电压幅值误差修正结果如图5所示。

图5 电压误差修正结果

从图5中可以看出，用本文所提方法修正后的电压值为规定的220 V电压，且修正结果具有较高的稳定性，一直保持在220 V，由此可知本文所提方法具有较好的电压修正效果。

2)电流误差修正。

本文在电流测量中采用了高精度测量方式，设置标准源输出频率为50 Hz、电压为220 V，电流的变化范围为±1.5 A。得到的电流幅值修正结果如图6所示。

图6 电流误差修正结果

分析图中电流修正结果可得，在电流修正前，部分电流值波动超过标准范围，此种现象容易导致电力系统出现故障。而修正后的电流值始终在规定的标准范围内，说明本文所提方法能够有效修正电流误差，保证电力系统的稳定运行。

3)相位角误差修正。

设置多功能标准源的输出频率为50 Hz、电压为220 V、电流为1 A，标准相位角设定为30°，得到的相位角误差修正结果如图7所示。

图7 相位角修正结果

从图7可以看出，修正前的最大误差角度为70°，修正后最大误差角度为15°，说明本文所提方法虽然能够修正大部分的相位角误差，但相位角修正结果仍需进一步优化。

综上所述，在电压幅值、电流幅值、电流电压间相位角的修正测试中，经过本文所提方法修正后的各项误差均取得显著效果，证明该误差修正方法是有效的。

3 结束语

本文给出的PMU暂态脱机检测误差修正方法可以增强弱信号，为修正电压幅值、电流幅值及电流电压间相位角提供一定的技术支持。由于条件限制，此次研究仅在仿真平台收集了固定的采样周期与采样时间的数据，后续还需要在实例中扩大数据采集范围验证本文方法的可靠性。在未来的研究中，也需要考虑电网中存在谐波、低频振荡等扰动情况，以优化相位角修正的结果。