基于热力学涡旋压缩机涡旋盘的结构设计优化

陈洪辉

（广东吉洪茂医疗科技有限公司，广东 佛山 528303）

涡旋压缩机时通过动涡旋盘和静涡旋盘啮合来实现气体压缩。涡旋盘变形后，初始啮合间隙会发生改变，啮合间隙过大，会导致涡旋压缩机泄漏严重，而啮合间隙过小，则会发生干涉撞齿。因此，涡旋盘啮合间隙与涡旋压缩机的性能具有直接关系，影响到压缩机是否能够稳定运行。基于热力学来分析压缩机涡旋盘温度和热变形后各个位置的啮合情况，优化涡旋盘结构，能够有效地提升涡旋压缩机的性能。

1 涡旋压缩机的结构设计

1.1 动涡旋盘的设计

涡旋齿的结构参数包括：涡旋齿齿高h、齿厚t、节距Pt以及涡旋齿圈数n、涡旋盘直径D等。如图1。涡旋齿圈数n是指涡旋齿型线在涡旋盘上的圆弧长度。圈数过多会造成涡旋压缩机整尺寸过大，整机体积和重量也随之增加，圈数太少会使压力达不到设计值。在工程上涡旋齿圈数一般是根据生产实际中的经验值来选取，一般取值为2～5圈。表1为涡旋盘基本结构参数。

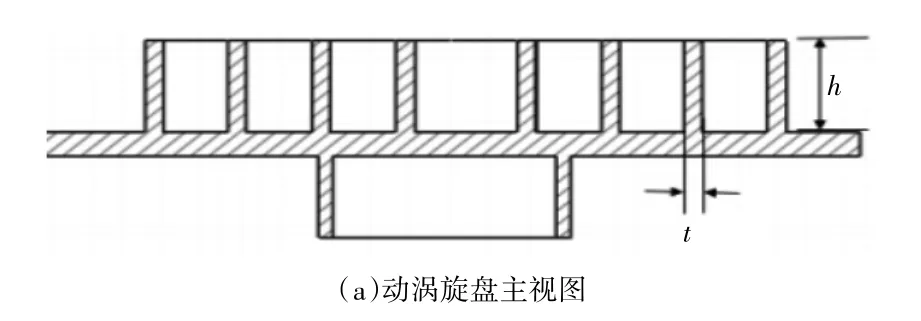
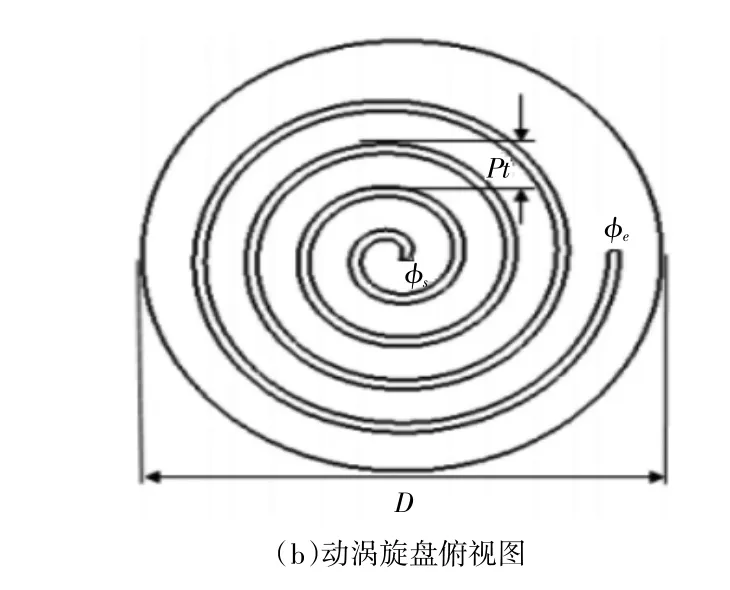
图1 涡旋齿结构参数示意图

表1 涡旋盘结构基本参数

根据设置的涡旋盘基本结构参数，对涡旋盘结构进行了设计。动涡旋盘的正面为涡旋齿，通过与静涡旋齿啮合实现气体压缩。动涡旋盘背面中心具有主轴轴承座，动涡旋盘通过与主轴过盈配合联接。在底板边缘，共有三个呈圆周分布的轴承座，其中设有偏心小轴。在偏心小轴的作用下，动涡旋盘进行偏心平移。主轴轴承座周边均匀分布有加强筋，可以增加涡旋盘底板强度。为了减少轴向泄漏，在涡旋齿的上部开有密封槽，并用聚四氟乙烯密封。

1.2 静涡旋盘的设计

静涡旋盘的前表面中心为涡旋齿，其结构参数与动态涡旋盘的结构参数相同。由于压缩机的吸入和排出需要，需要在涡旋盘上设计一个吸入和排出孔。在气体压缩过程中，压缩腔从涡旋齿的周边向内部逐渐移动，使排气孔位于涡旋齿的中心，靠近齿头。在齿啮合过程中，应形成两个对称的吸气腔。为了满足进气的需要，节省涡旋盘空间，在两个吸气腔之间的距离附近设置进风口[1]。为了提高压缩过程中各压缩腔的密封效果，在涡旋盘涡旋齿顶部和外缘设置密封槽。另外，在气体压缩过程中，由于外部工作产生的大量热量，涡流的温度会迅速升高，所以在静涡旋盘背部增加风冷系统，提高压缩效率，减少温度变化对涡旋盘应力和的影响。

图2 静涡旋盘几何模型

2 动、静涡旋盘温度场与结构变形仿真

2.1 动、静涡旋盘温度场仿真分析

为了获得动、静涡旋压缩机的温度场，必须计算涡旋压缩机的热力学过程。目前，国内外对压缩室内对流换热的研究已经取得了很多成果，但在分析压气机盘温度场时，温度边界条件过于简化。在稳态条件下，虽然涡旋盘上的温度不随主轴旋转角度而变化，但压缩腔内气体温度的周期性作用导致涡旋盘上的温度分布。因此，为了获得更合理的涡旋盘温度，提出了一种计算涡旋盘热边界的新方法。

2.1.1 涡旋盘热载荷分析与计算

在对温度场进行有限元分析时，有必要确定其热边界条件，因此，首先分析了涡旋压缩机涡旋盘的热负荷[2]。动涡旋盘上的热量主要来自工作腔中的压缩气体与涡旋盘表面之间的对流换热。除了与压缩腔中的空气进行对流换热外，静态涡旋盘还受到由后部风冷的对流换热，所以，提出了涡旋盘热边界计算时的假设：

（1）假定每个压缩腔内的气体状态参数相同。

（2）对于动涡旋盘，仅考虑与压缩腔内气体接触的涡旋齿表面的对流传热，其他涡旋盘的表面可视为绝热处理。

（3）对于静态涡旋盘，仅考虑与压缩腔内气体接触的涡旋齿表面的对流换热和外部冷却的对流传热，而静态涡旋盘上的其他表面被视为绝热处理。

2.1.2 建立有限元模型

为了避免关键部件因为网格退化导致的计算失真，忽略了动静涡旋盘的一些不必要的特性[3]。在进行有限元分析之前，必须将三维模型导入到ANSYS Workbench中。然后对于动、静涡旋盘进行网格划分，网格划分方式采用结构网格划分中的自由网格划分方法，将网格单元的最小尺寸设置为2.5 mm。网格采用十节点四面体高阶单元。内部中间节点被添加到四面体的每条边上，并使用高阶多项式进行插值。涡旋盘由铸造铝合金制成。材料参数可以在ANSYS中设置。铸造铝合金材料的特征参数见表2。

表2 压铸铝合金的材料特性参数

2.1.3 仿真结果

对动、静涡旋盘的有限元模型施加荷载，然后经过求解获得它们的温度场分布情况。如图3和图4所示。从图中可以看出，温度场分布从中心到外围逐渐减小，但温度分布不易观察到。为了详细分涡旋盘的轴向和径向温度分布，建立了以涡旋齿尾处为起点、弧长为横坐标、温度为纵标系的坐标系。从底部到顶部，每隔相同距离，并绘制六个不同的齿高。而动涡旋盘和静涡旋盘涡旋齿上的分布情况中，温度从头部到尾部逐渐降低，头部附近的温度变化迅速，尾部附近的温度变化缓慢[4]。

图3 动涡旋盘温度场云图

图4 静涡旋盘温度场云图

2.2 动、静涡旋盘结构变形仿真分析

通过热-结构耦合模拟，可以得到板的动态和静态结构变形。热-结构耦合可分为直接耦合和顺序耦合[5]。将温度场模拟结果作为热载荷直接加载到静力分析中，采用顺序耦合法模拟动、静态位移盘的结构变形。在温度场分析中，建立了涡流板的有限元模型。因此，将位移约束和静载荷约束添加到静力分析中。

求解动态和静态涡旋盘有限元模型，获得动态涡旋盘的整体变形。如图5和6所示，动涡旋盘的总变形从中心到边缘逐渐增加。这是因为位移盘后部的轴承孔与主轴之间存在干涉，从而限制了轴承孔的底面。因此，位移板只能沿轴承孔的周边向外延伸。同时，可以看出，在位移盘的中心，位移齿从下齿向上齿有明显的趋势。这主要是由于温度沿动涡旋盘高度移动。随着温度沿高度方向产生弯曲应力，涡流向外扩展。为了实现动涡旋盘位移在各个方向上的具体变形，建立了以尾齿位移和弧长为横坐标、位移为纵坐标的坐标系，分别提取了上齿位移的轴向位移和径向位移[6]。

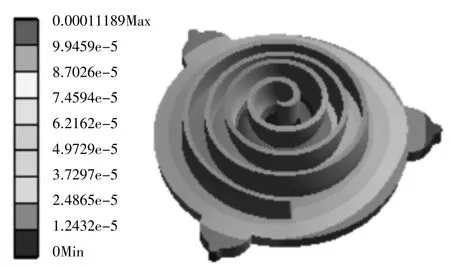
图5 动涡旋盘整体位移云图

在径向上，静涡旋齿顶的变形趋势呈周期性变化，但随着离心弧长的增加，变形量的数值逐渐减小。在轴向上，静涡旋齿的变形趋势与径向方向变形相似，但也呈现出周期性的不规则波动，然后变形逐渐减小。

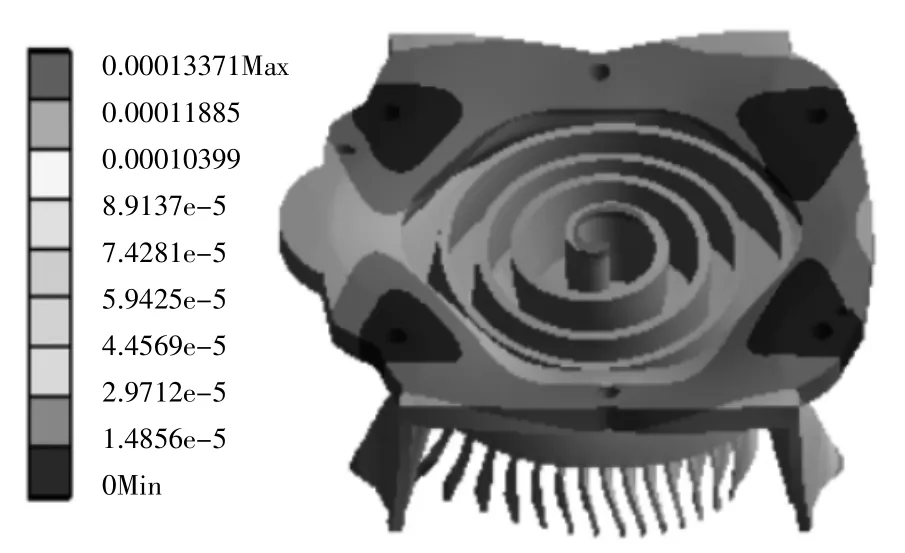
图6 静涡旋盘整体位移云图

3 涡旋齿厚度对压缩机排量的影响分析

为了解不同齿厚对压缩机排气性能的影响，分别模拟了齿厚为2 mm、3 mm、4 mm和5 mm时的结构变形，获得了不同齿厚的涡旋压缩机动、静涡旋盘重新建模，进行结构变形仿真分析。根据建立的变形分析数学模型，对仿真结果进行了处理，得到了不同齿厚动、静态滑动盘的径向和轴向变形。因为干涉分析的目的是获得啮合点处的齿位移畸变随延伸角的变化，而压缩机位移分析的目的是分析压缩机位移随主轴旋转角的变化。将动、静涡旋盘随涡旋展角变化的干涉值置换为对应主轴转角下的啮合点处的干涉值。当主轴旋转角度为0°时，涡旋压缩机的吸入室腔关闭，与网格点相对应的动、静涡旋齿内测的最终展角为1530°。当主轴旋转角度增大1°时，相关啮合点的最终扩张角减小1°，从而实现涡旋压缩机从吸气到排气过程中动、静涡旋齿啮合点处的径向干涉值随主轴转角的变化情况。如图7、8所示。

图7 动涡旋齿外侧与静涡旋齿内侧干涉情况

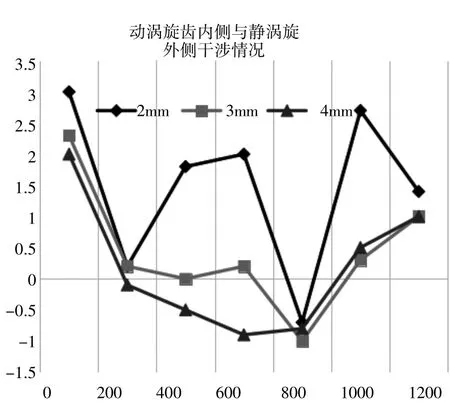
图8 动涡旋齿内侧与静涡旋齿外侧干涉情况

从图7、8中可以看出，齿厚的变化对于涡旋齿的干涉影响非常小，但是会对干涉值大小造成影响。随着齿厚的增加，在发生干涉的区域，静涡旋齿外侧和动涡旋齿内侧的干涉值会逐渐增加。根据压缩机排量计算数学模型，获得了不同齿厚下涡旋压缩机压缩腔的质量的变化曲线，了解齿厚变化对压缩机排量的影响，如图9所示。

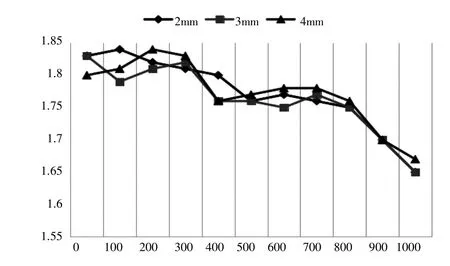
图9 不同涡旋齿厚度涡旋压缩机排量变化曲线

4 结语

基于涡旋压缩机开展热力学来优化涡旋盘结构，通过优化涡旋压缩机涡旋盘结构的基本参数，分析了涡旋压缩机涡旋盘单一结构参数和组合结构参数下的排量变化，表明涡旋齿厚度及涡旋盘底板厚度的变化都会对压缩机最终排量产生影响。