基于幅值调制的炮击振动实验室模拟方法

蔡涵翔 袁宏杰 徐俊

基于幅值调制的炮击振动实验室模拟方法

蔡涵翔1袁宏杰1徐俊2

（1 北京航空航天大学，北京 100083；2 中国航空综合技术研究所，北京 100028）

现有的炮击振动信号模拟方法基于平稳、高斯分布的振动，模拟了自功率谱密度等低阶统计特征。但炮击振动信号具有非平稳、非高斯特点，对于这类具有瞬态重复特性炮击振动信号的高阶特征模拟问题，基于目标峭度值与指数函数迭代计算指数参数值并生成调制信号，对平稳高斯信号进行幅值调制后生成炮击振动模拟信号。在实例验证中，通过对比炮击振动模拟信号与实测炮击信号的功率谱密度（PSD）、峭度值、疲劳损伤谱、冲击响应谱验证了方法的有效性。

炮击振动；峭度；近似模拟方法；指数函数；调制信号

0 引言

炮击振动响应具有时间短、量值高、具有重复性等特点[1]，模拟炮击振动的传统方法是基于PSD谱，利用随机加正弦方法生成时域信号[2]，该信号为平稳的高斯分布的信号、频域特征与实际炮击振动信号类似。但实际炮击振动信号具有瞬态冲击特性，其均方值随时间而变化，说明它是非平稳信号；其峭度大于3，说明它是超高斯信号。利用PSD谱对炮击振动信号进行模拟，仅仅能反映出均值、均方值等低阶统计量，而无法反映出其瞬态冲击特性和偏度、峭度等高阶统计量。同时，用高斯信号激励模拟非平稳非高斯激励，可能会得出比实际低的疲劳损伤估计[3]。

目前对于炮击振动信号的模拟方法[1,4,5]主要是基于均值、标准差等低阶特征，利用小波变换、自协方差矩阵等方法对炮击振动信号进行模拟,而对峭度等高阶特征考虑较少。在非高斯信号的模拟方法研究中[6-11]，多项式变换、幅值调制和相位重构等许多方法被提出，使模拟信号的峭度达到目标值。针对现有方法对峭度等高阶特征考虑不足的缺点，参考非高斯信号的模拟方法，本文基于幅值调制方法[12]和时域随机化方法，结合炮击振动信号重复瞬态冲击的时域特性，提出一种利用目标峭度值和指数函数生成调制信号，最终生成炮击振动模拟信号。并利用PSD谱、疲劳损伤谱和冲击响应谱验证方法有效性。

1 实测炮击振动的信号特征分析

通过实际测试得到炮击振动外场数据如图1，其采样频率为8192Hz，采样点为8192。

图1 实测炮击振动信号

1.1 功率谱密度（PSD）

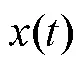
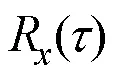
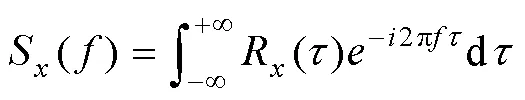
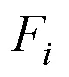
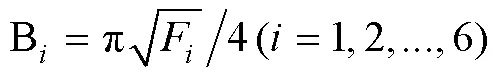
依据图2所示试验谱，采用正弦加随机方法（SOR），由宽带随机振动谱生成平稳随机信号，由正弦窄带峰生成正弦信号，二者叠加生成模拟炮击振动信号如图3所示，其PSD谱如图4所示，可以看出基于SOR的模拟炮击振动数据的PSD谱与试验谱较为符合。

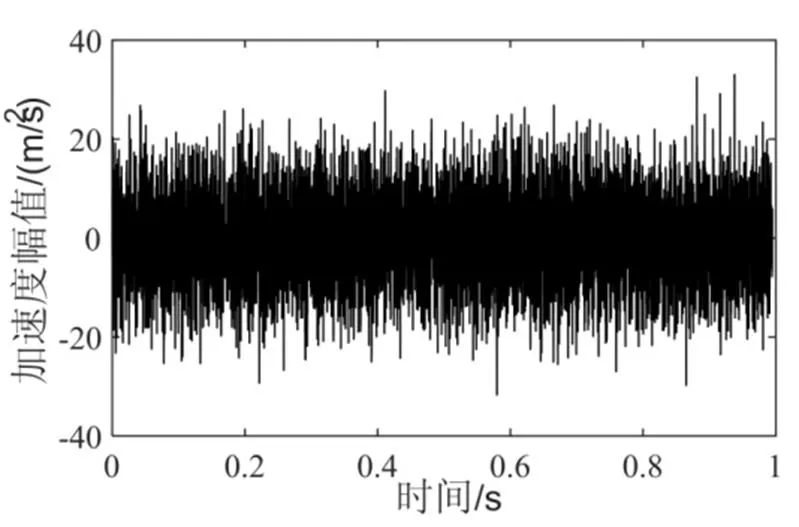
图3 模拟炮击振动信号(SOR)

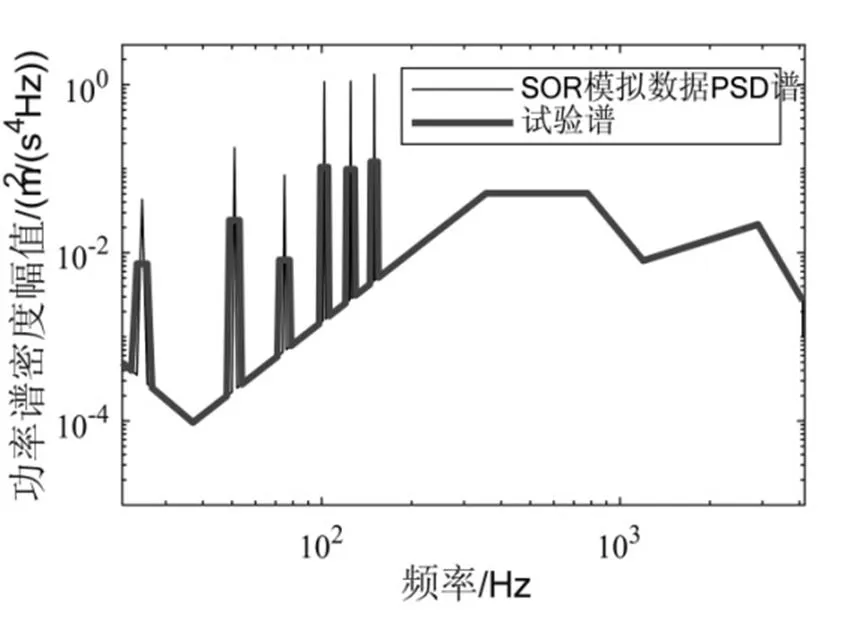
图4 模拟信号PSD谱及试验谱(SOR)

1.2 高阶特征

实际情况下，炮击振动信号等大多数实测信号幅值的PDF均不服从高斯分布，通常称之为非高斯信号。由于PSD只能表征信号标准差等低阶特征，工程上增加偏度、峭度等高阶特征来描述非高斯信号。长度为的离散幅值数据的偏度、峭度计算式为

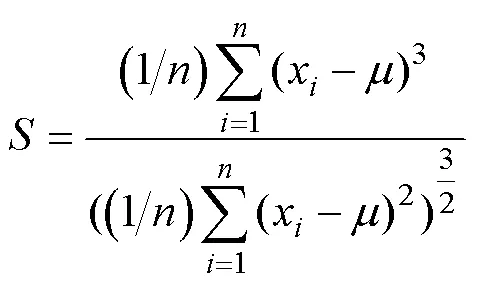
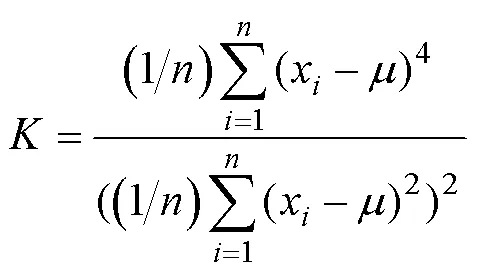
1.3 包络分析

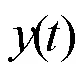
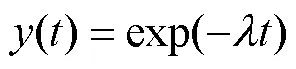
2 炮击振动信号模拟方法

依据第二章中所得实测炮击振动信号的PSD谱、峭度等特征作为模拟炮击振动信号生成依据。使用正弦加随机（SOR）方法生成平稳模拟信号；利用时域随机化方法生成目标长度的随机的平稳模拟信号；基于时域加窗方法[12]，利用指数函数产生窗函数，合成指定峭度的炮击振动信号。

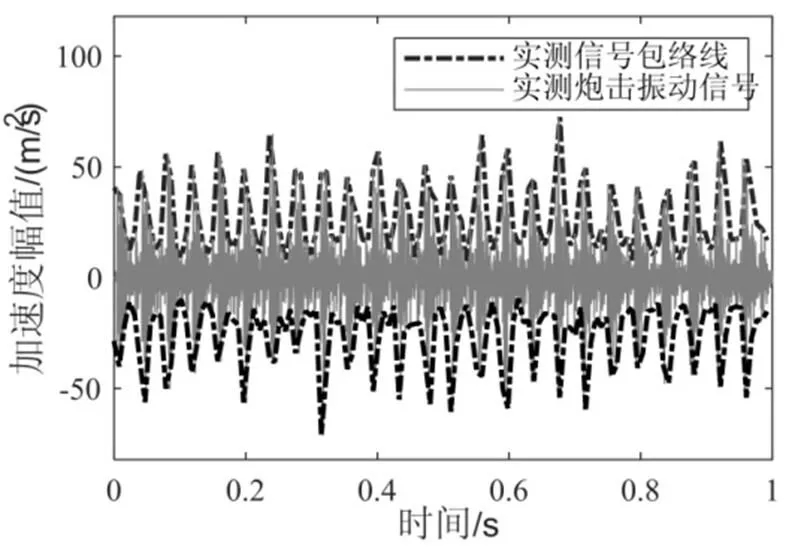
图5 实测炮击振动信号包络线

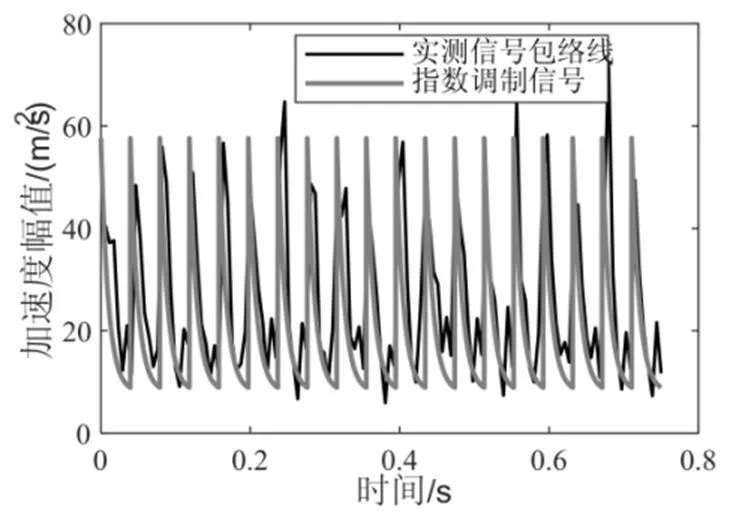
图6 指数函数与包络线

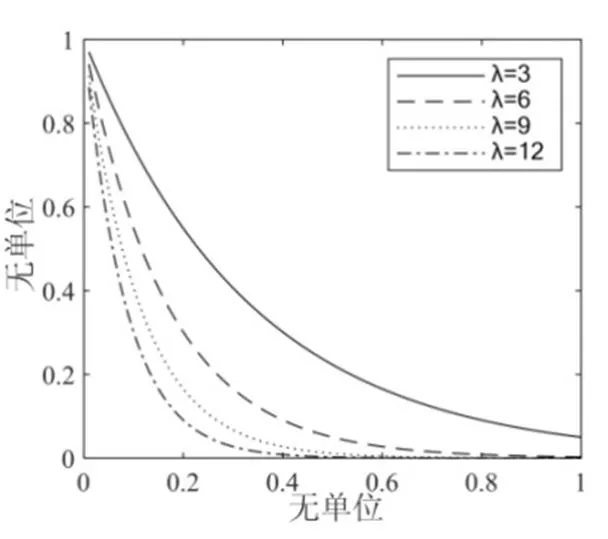
图7 不同参数下的指数函数图像

2.1 平稳模拟信号生成

2.1.1 正弦部分

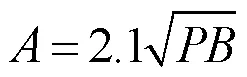
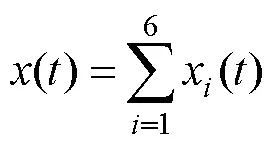
2.1.2随机部分

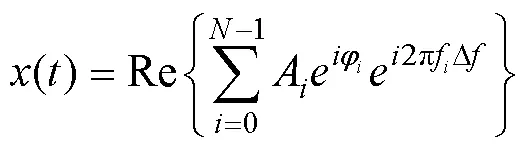
(11)

2.2 平稳模拟信号的时域随机化

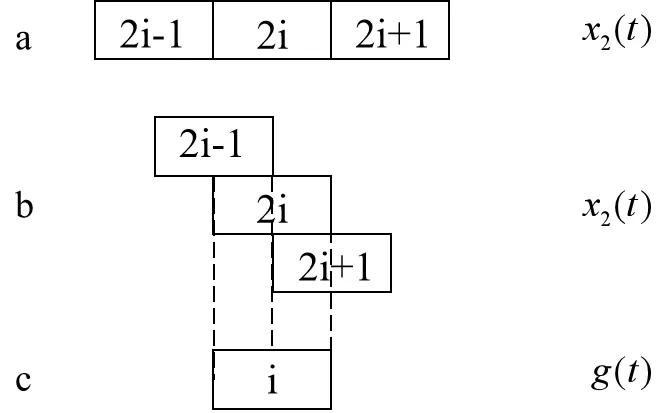
图8 信号叠加过程

2.3 生成窗函数

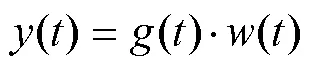
如图1所示，炮击振动信号在时域上具有如下特点：具有周期性，该周期与武器装备射速相关；具有脉冲冲击特性，单发炮击信号先有一个剧烈上升的冲击，随后快速衰减。根据1.3节中的包络分析结果，炮击振动信号的脉冲冲击特性与指数函数图像特征相吻合，故选取指数函数生成窗函数对平稳高斯信号进行调制。以炮击周期T为周期生成指数窗口，在第个周期上的窗函数为

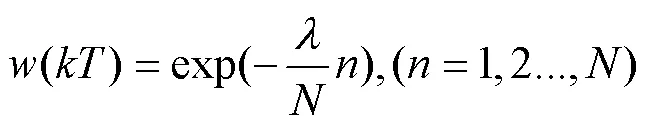
2.4 合成炮击振动信号

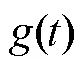
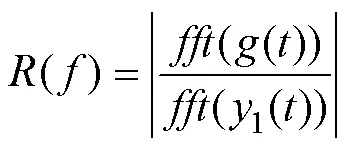
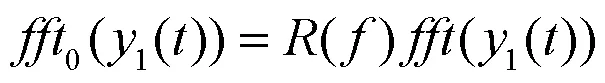
3 实例分析

3.1 实测数据特征

以图1所示实测炮击振动信号数据为例，该数据采样时间为1s，采样频率为8192 Hz，采样点数为8192，偏度值为0.061，峭度值为6.398，其PSD谱如图2所示，该数据显示其炮击频率为25 Hz。

3.2 平稳模拟信号生成

利用正弦加随机方法和时域随机化方法生成时间长度为10 s，数据点数为81920的平稳模拟信号如图9所示，其偏度值为0.022，峭度值为2.965，该信号的PSD谱如图10所示。

3.3 生成窗函数

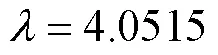
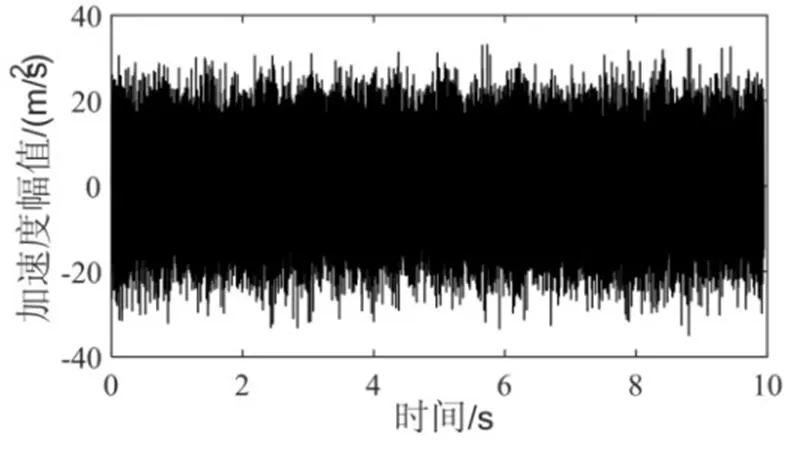
图9 平稳模拟信号

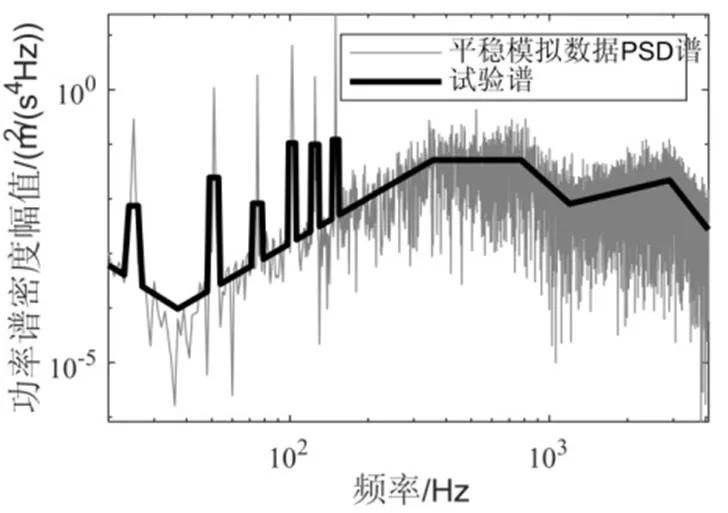
图10 平稳高斯信号的PSD谱与试验谱

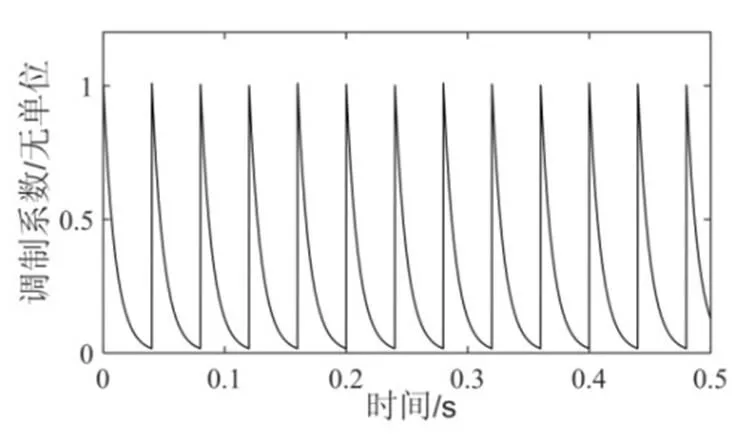
图11 窗函数

3.4 合成模拟炮击振动信号

基于时域加窗方法，将平稳高斯信号与窗函数相乘，得到模拟炮击振动信号如图12。其偏度值为0.013，峭度值为6.3983，与实测炮击振动信号峭度相近。其PSD谱如图13，可见模拟信号和试验谱较为接近。

3.5 疲劳损伤谱与冲击响应谱

除了PSD谱和峭度值外，还可以使用疲劳损伤谱（FDS）与冲击响应谱（SRS）来进一步评估模拟振动信号的有效性。FDS描述了在给定输入振动激励下疲劳损伤随固有频率变化的情况。图14为模拟炮击振动信号与实测炮击振动信号的FDS。SRS描述了系统在给定输入振动激励下最大响应随固有频率变化的情况。计算不同固有频率下单自由度系统加速度响应的最大值，即可绘制SRS。

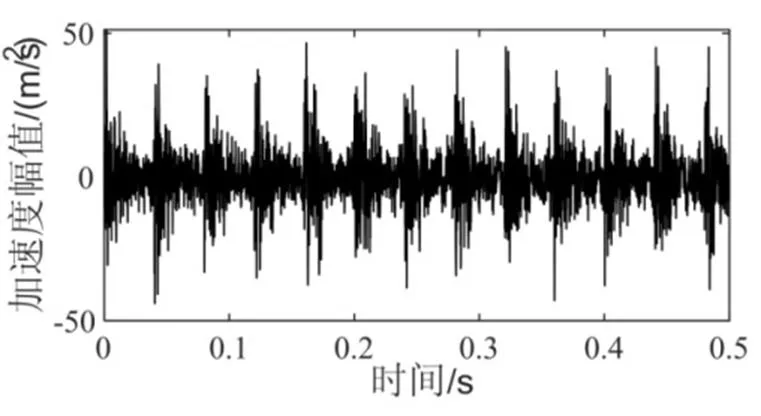
图12 模拟炮击振动信号

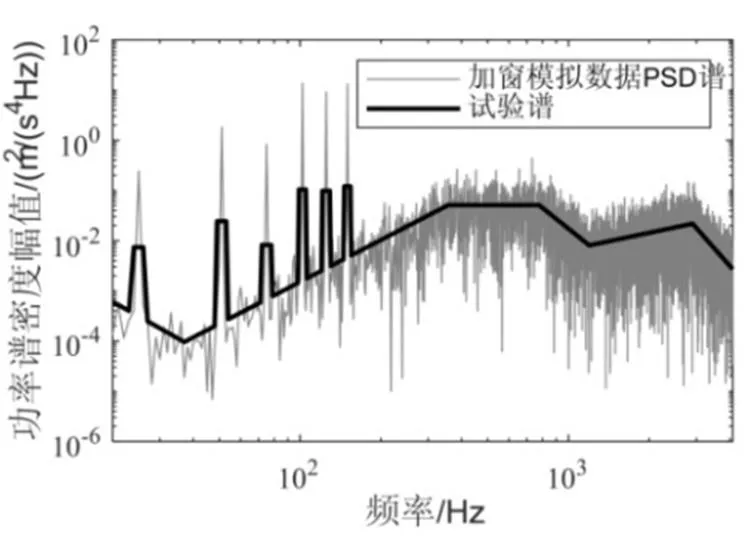
图13 模拟炮击振动信号PSD谱与试验谱

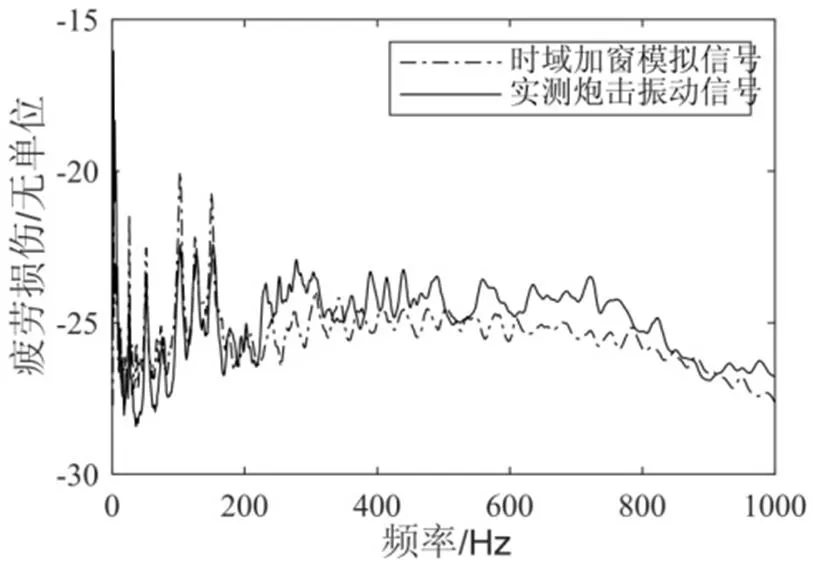
图14 模拟与实测炮击振动信号的疲劳损伤谱(FDS)

图15为模拟炮击振动信号与实测炮击振动信号的SRS。由图14、图15可以看出，模拟炮击振动信号与实测炮击振动信号的FDS与SRS均很接近。对数坐标下，二者误差平均值分别为3.44%和5.77%，验证了模拟炮击振动信号生成方法的正确性。

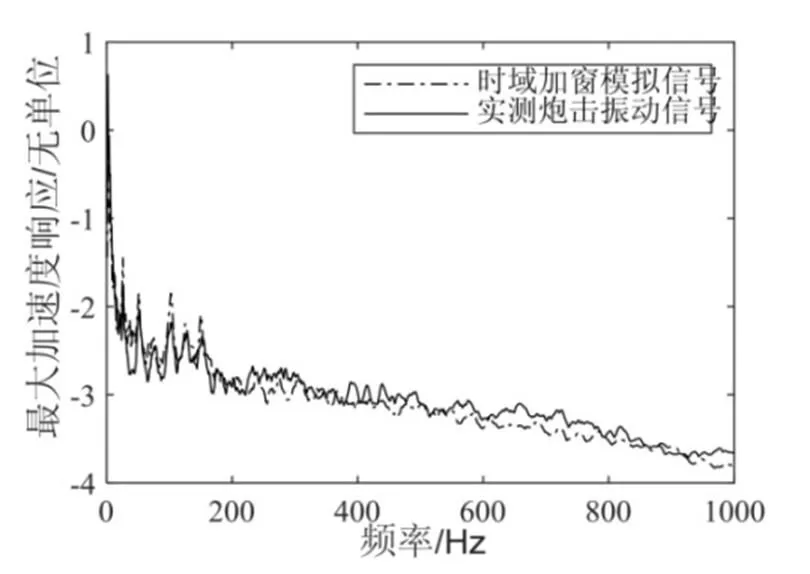
图15 模拟与实测炮击振动信号的冲击响应谱(SRS)

4 结论

本文提出基于时域加窗生成模拟炮击振动数据的方法，利用指数函数生成窗函数对信号进行幅值调制，采用迭代的方法寻找合适的指数参数确保模拟信号与实测信号具有相同的峭度。与目前采用的基于均值、方差等低阶特征的炮击振动信号模拟方法相比，时域加窗方法基于峭度这一高阶特征设计窗函数，使模拟信号在确保均值、方差等低阶特征符合要求的基础上实现对峭度的高精度、可控的模拟。实例验证中，模拟信号与实测信号具有相近的PSD谱和峭度值，二者FDS与SRS相近，验证了方法的正确性。本文提出的基于时域加窗的炮振数据模拟方法适用于具有重复瞬态冲击特性炮击振动的实验室模拟，通过对方法中窗函数的设计，可以将应用范围扩展到其它具有重复特性的非平稳振动模拟中。

[1] 徐明, 孙建勇. 飞机炮击环境分析及模拟方法研究[J]. 环境技术, 2002(2): 11-14. [XU Ming, SUN Jianyong. Research of airplane gunfire environment analysis and simulation method [J]. Environmental Technology, 2002(2): 11-14. ]

[2] DoD. Environment engineering consideration and laboratory test: MIL-STD-810G[S]. USA: Naval Publications and Form Center, 2008: 10.

[3] Palmieri M, Cesnik M, Slavic J, et al. Non-Gaussianity and non-stationarity in vibration fatigue [J]. International Journal of Fatigue, 2017, 97: 9-19.

[4] Smallwood D O. Characterization and simulation of gunfire with wavelets. 1998.

[5] Smallwood D O. Characterization and Simulation of Gunfire with Karhunen-Loeve Expansion[J]. Journal of the Iest, 2004, 47:47-50.

[6] Steinwolf A. Closed-loop shaker simulation of non-Gaussian random vibration. Part 1: Discussion and methods [J]. Test Engineering and Management, 2006, 68(3):10-13.

[7] Steinwolf A. Closed-loop shaker simulation of non-Gaussian random vibration. Part 2: Numerical and experimental results [J]. Test Engineering and Management, 2006, 68(5):14-19.

[8] Steinwolf A. Random vibration testing with kurtosis control by IFFT phase manipulation[J]. Mechanical Systems & Signal Processing, 2012, 28: 561-573.

[9] Xu F, Li C,Jiang T.On the shaker simulation of wind-induced non-Gaussian random vibration [J].Shock and Vibration, 2016(2):1-10.

[10] Ronghui, ZHENG, Huaihai, et al. Control method for multi-input multi-output non-Gaussian random vibration test with cross spectra consideration [J]. Chinese Journal of Aeronautics, 2017.

[11] 蒋瑜, 陶俊勇, 王得志, 等. 一种新的非高斯随机振动数值模拟方法[J]. 振动与冲击, 2012, 31(19): 169-173. [Jiang Y , Tao J Y , Wang D Z , et al. A novel approach for numerical simulation of a non-Gaussian random vibration [J]. Journal of Vibration and Shock, 2012, 31(19): 169-173.]

[12] Hale M T, Corporation T. Synthesis of a time history based on the sine-on-random prediction methodology defined in MIL-STD-810 Method 519[J].Journal of the IEST, 2017, 60(1): 31-41.

[13] GJB 150. 20A-2009. 中国人民解放军总装备部.军用装备实验室环境试验方法第20部分: 炮击振动试验[S]. 2009.

[14] 蒋瑜, 陈循, 陶俊勇. 基于时域随机化的超高斯真随机驱动信号生成技术研究[J]. 振动工程学报, 2005, 18(4): 4. [Jiang Y , Chen X , Tao J Y . Study on the generation of super-Gaussian and true-random drive signals using time domain randomization[J]. Journal of Vibration Engineering, 2005, 18(4): 4.]

[15] 吴家驹, 贺智国, 王璟南.非平稳随机振动与烈度控制[J]. 强度与环境, 2019, 46(2):6.[Wu JiaJu, He ZhiGuo, Wang JingNan. Non-stationary random vibration and intensity control [J]. Structure & Environment Engineering,2019, 46(2): 1-6.]

A New Laboratory Simulation Method of Gunfire Vibration

CAI Han-xiang1YUAN Hong-jie1XU Jun2

(1 School of Reliability and Systems Engineering, Beihang University, Beijing 100083, China; 2 China Aero-Ploytechnology Establishment, Beijing 100028, China)

The existing simulation method of gunfire vibration signal simulated the time domain characteristics and the low-order statistical characteristics such as mean and variance. While the signal’s high-order characteristics were ignored. To solve the high-order characteristic simulation problem of non-stationary, non-Gaussian gunfire vibration signals with transient repetitive pulse characteristics, the modulation signal was constructed by exponential function. The exponential parameter value was iteratively calculated based on the target kurtosis value to generate the modulation signal. The Gaussian signal was amplitude modulated to generate the gunfire vibration simulation signal. The effectiveness of the method is verified by comparing the power spectral density (PSD), kurtosis, fatigue damage spectrum and shock response spectrum of the simulated and measured gunfire vibration signals.

Gunfire vibration; Kurtosis; Approximate simulation method; Exponential function; Modulating signal

V414.3+3

A

1006-3919(2022)03-0052-07

10.19447/j.cnki.11-1773/v.2022.03.008

2022-03-02；

2022-05-23

蔡涵翔(1999―)，男，硕士生，研究方向：可靠性与环境试验；(100083)北京市海淀区学院路37号.