基于多通道自适应滤波算法的主动降噪试验

高博 张忠 魏龙 侯传涛 任方 秦朝红 郭静

基于多通道自适应滤波算法的主动降噪试验

高博 张忠 魏龙 侯传涛 任方 秦朝红 郭静

(北京强度环境研究所可靠性与环境工程技术重点实验室，北京 100076)

前馈自适应控制算法因其运算量小、容易实现、物理机理清晰等优点而在噪声主动控制中被广泛应用。目前工程中噪声主动控制的应用案例主要采用单通道噪声主动控制算法，多通道控制算法相较于单通道控制算法控制效果更好，但由于结构较复杂，工程应用较少。因此，本文对多通道自适应滤波算法进行改进，并通过试验验证其有效性，为多通道噪声主动控制系统的工程应用提供一种可行方案。

噪声主动控制；多通道Fx-LMS算法；离散状态空间方程；泄漏因子

0 引言

噪声控制技术分为被动控制与主动控制两种方式[1]。被动控制技术主要通过在结构表面铺设弹性阻尼材料达到吸声、隔声的效果，这种方法应用最广，对于中高频噪声具有较好的控制效果，但对低频噪声控制效果较差[2]。主动控制技术是利用声波干涉相消原理[3]，通过生成与噪声源振动频率与幅值相同、相位相反的声波，并与噪声源叠加，从而达到以声消声的目的。相较于被动控制技术，该方法更适合于低频噪声的控制，因而主动控制技术在汽车、船舶、航空、航天等领域越来越受到重视[4-6]。

控制算法是噪声主动控制研究的核心问题，它的优劣会从本质上决定了整个控制系统性能的好坏，其中，前馈自适应控制算法因其运算量小、容易实现、物理机理清晰等优点而在噪声主动控制中被广泛应用。自适应控制理论的研究始于20世纪50年代，Widrow和 Hoff在1959年发明了一种随机梯度算法——最小均方（Least Mean Square,LMS）算法，它结构简单易于实现，被广泛应用于自适应信号处理。在这之后，学者们便努力将其应用到主动控制中来，最终形成了滤波最小均方（Fx-LMS）算法。这是一种考虑次级通道的LMS算法，并被广泛用于噪声主动控制中[7-9]。近年来，在自适应主动控制领域，Fx-LMS算法也在不断发展进化之中，形成了如归一化Fx-LMS算法、变步长Fx-LMS算法、泄露Fx-LMS算法、符号Fx-LMS算法，动量Fx-LMS算法等，改进的方向集中于加快自适应迭代收敛速度，降低控制稳态误差等[10-12]。经典的单通道自适应滤波噪声主动控制系统如图1所示，其中控制系统部分以参考信号S和误差信号e为输入，以控制扬声器的控制信号为输出。当噪声源、控制扬声器与噪声控制点的个数不为1时，则参考信号、误差信号及控制信号的个数不为1，即得到多通道控制算法如图2所示。

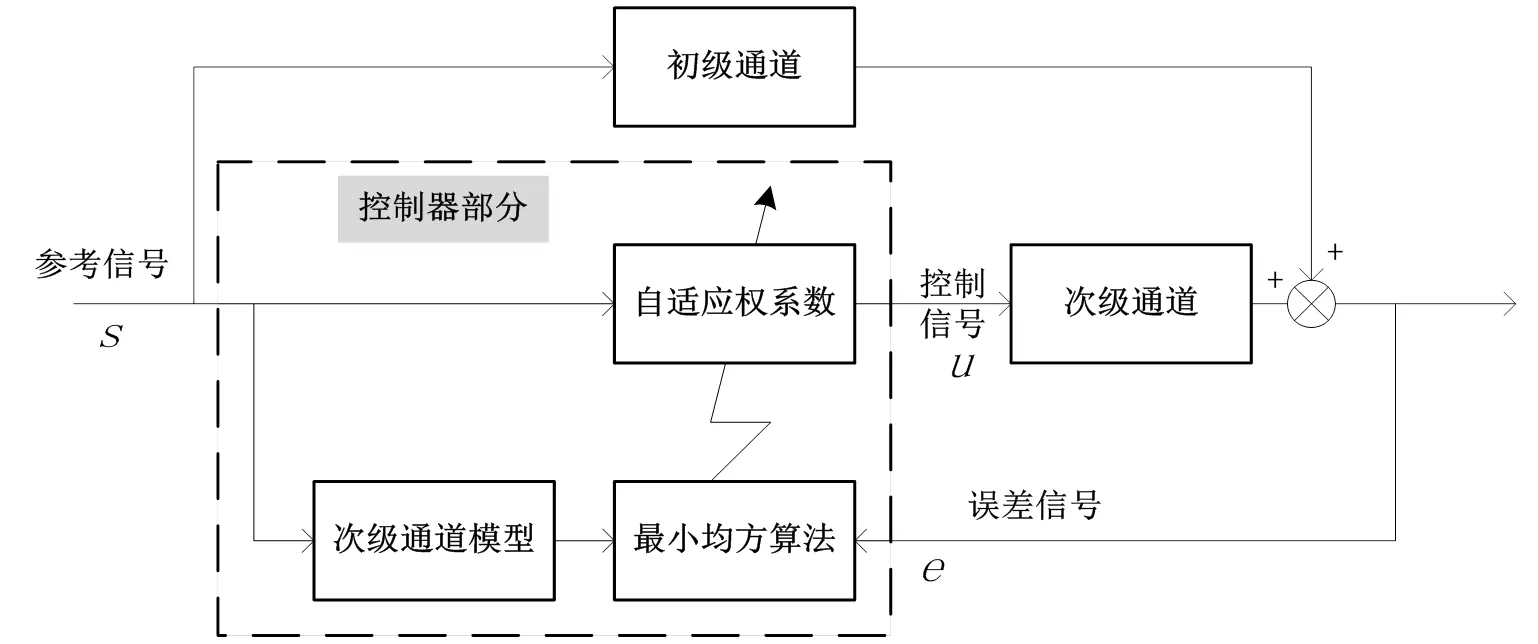
图1 前馈自适应滤波噪声主动控制系统框图

图2 多通道自适应滤波控制算法

对比图1与图2可以看出，当噪声源、控制扬声器与噪声控制点的个数增加时，控制算法的复杂度成倍增加，且算法形成后，噪声源个数、控制扬声器个数、噪声控制点个数均固定不可变，不利于工程使用。针对上述问题，本文对多通道自适应滤波控制算法进行改进，提出一种基于仿真平台的工程化的多通道控制算法，使得噪声源个数、控制扬声器个数、噪声控制点个数可灵活改变，为Fx-LMS算法的研究、多通道噪声主动控制系统的应用提供一种可行方案。

1 多通道自适应滤波控制算法实现

假设参考信号个数为I，控制扬声器个数为J，噪声控制点数为。*()表示变量*在第个时间步的值。则控制器实现方法如下。

1.1 参考信号合并

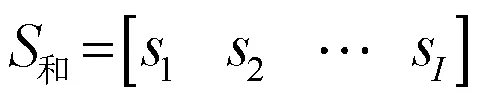
以I=2为例，在仿真平台中实现如图3所示

1.2 次级通道模型实现

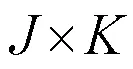
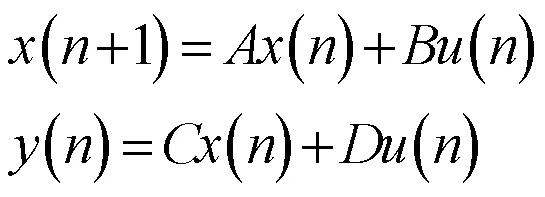
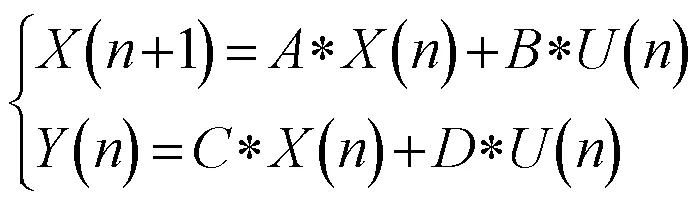
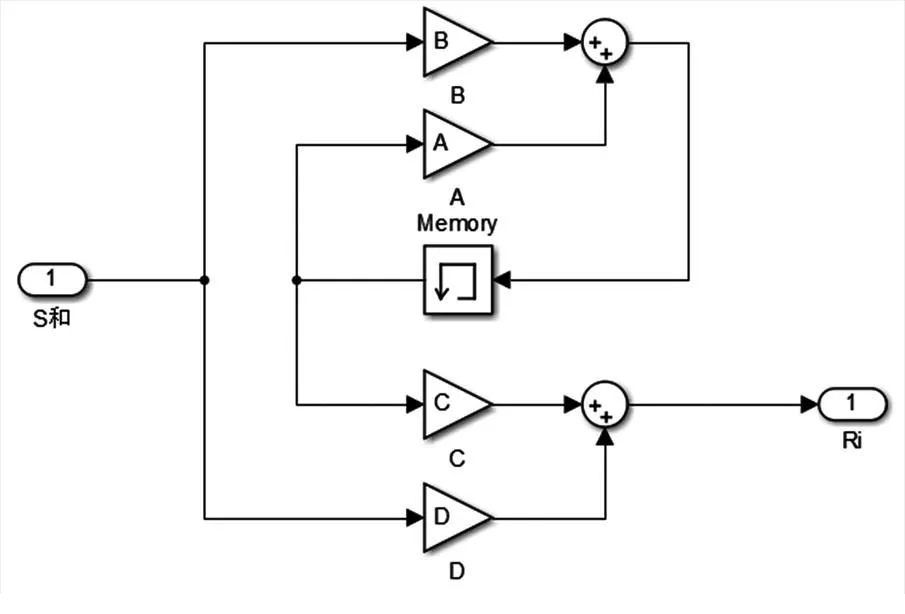
图4 离散状态空间方程

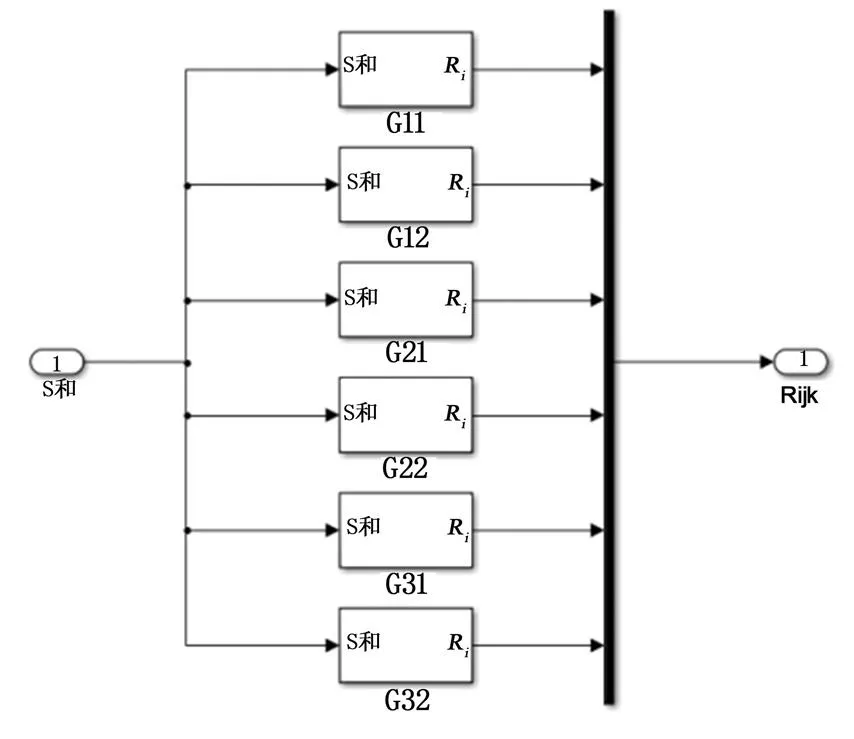
图5 次级通道滤波模块

以为输入变量矩阵，分别计算次级通道G的响应，得到滤波参考信号R=[12 ……I]。以=3，=2为例，次级滤波模块实现方法如图5所示。

1.3 自适应权系数更新方法

自适应权系数的迭代方法如式（4）所示，这里引入了泄漏因子并增加了权系数锁定开关，可增加系统稳定性，锁定开关可在控制效果接近最优之后，手动将权系数锁定为常值，避免持续迭代导致系统发散。

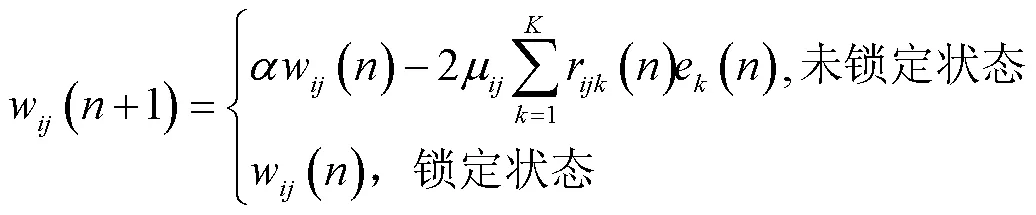
式中，mij为学习率。ek为第k个噪声控制点处的声压信号。权系数更新/锁定在仿真平台中实现方法如图6所示。

1.4 控制器输出计算方法

第个控制扬声器的控制信号可由式（5）计算获得。

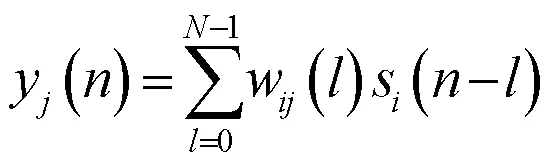
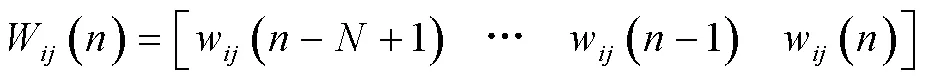
组合权系数的实现方法如图7图所示。

将s()组合为S()：需要注意S()的排序方式与权系数W()相反。

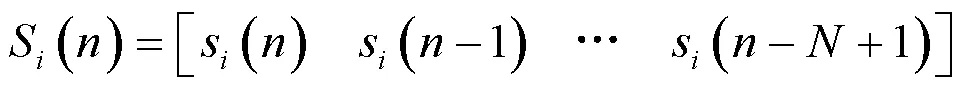
组合参考信号的实现方法如图8所示。

图8 组合参考信号

控制器输出可表示为

2 自由空间噪声主动控制试验验证

基于上述控制算法开展自由空间噪声主动控制试验验证，试验分为单通道控制试验和多通道控制试验。

2.1 单通道噪声主动控制试验

单通道噪声控制试验如图10所示，控制扬声器与噪声源音响相对放置，误差传声器位于二者之间中心位置。

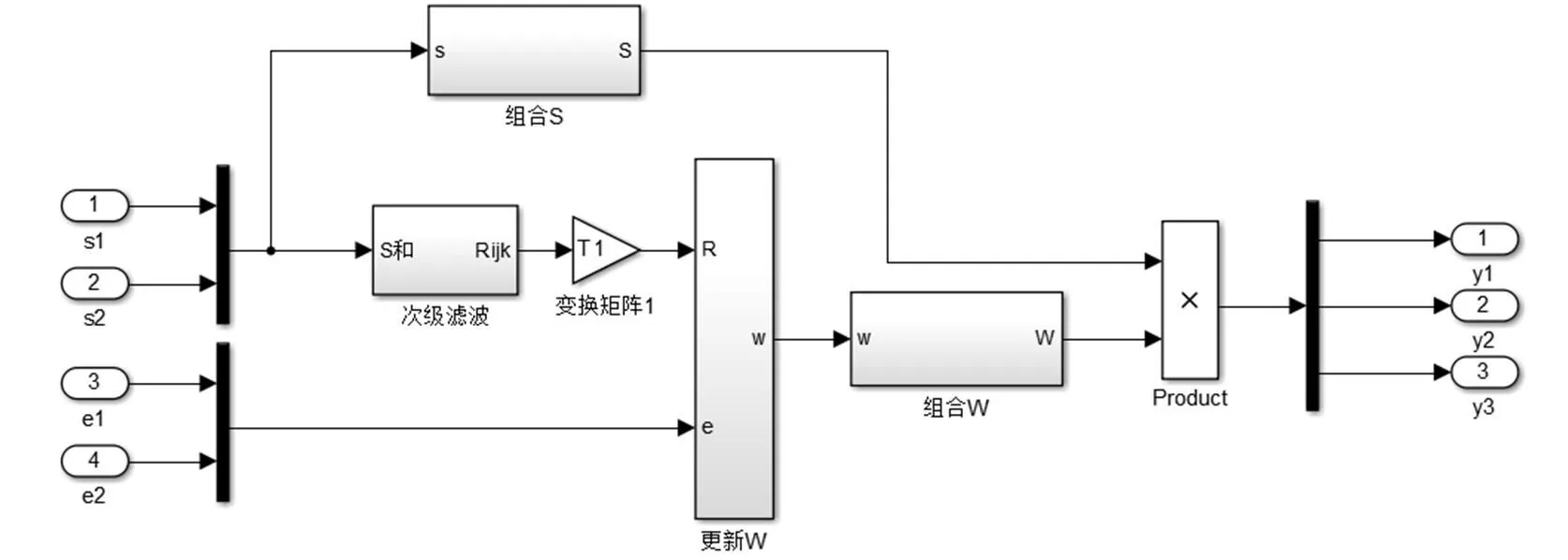
图9 改进的多通道自适应噪声主动控制算法

1-控制扬声器，2-噪声源音响，3-误差传声器，4、5、6-声场测量传声器

首先基于状态空间方法开展声场次级通道辨识，辨识得到的状态空间模型为6阶，辨识结果如图11所示，辨识精度达到99.99%。

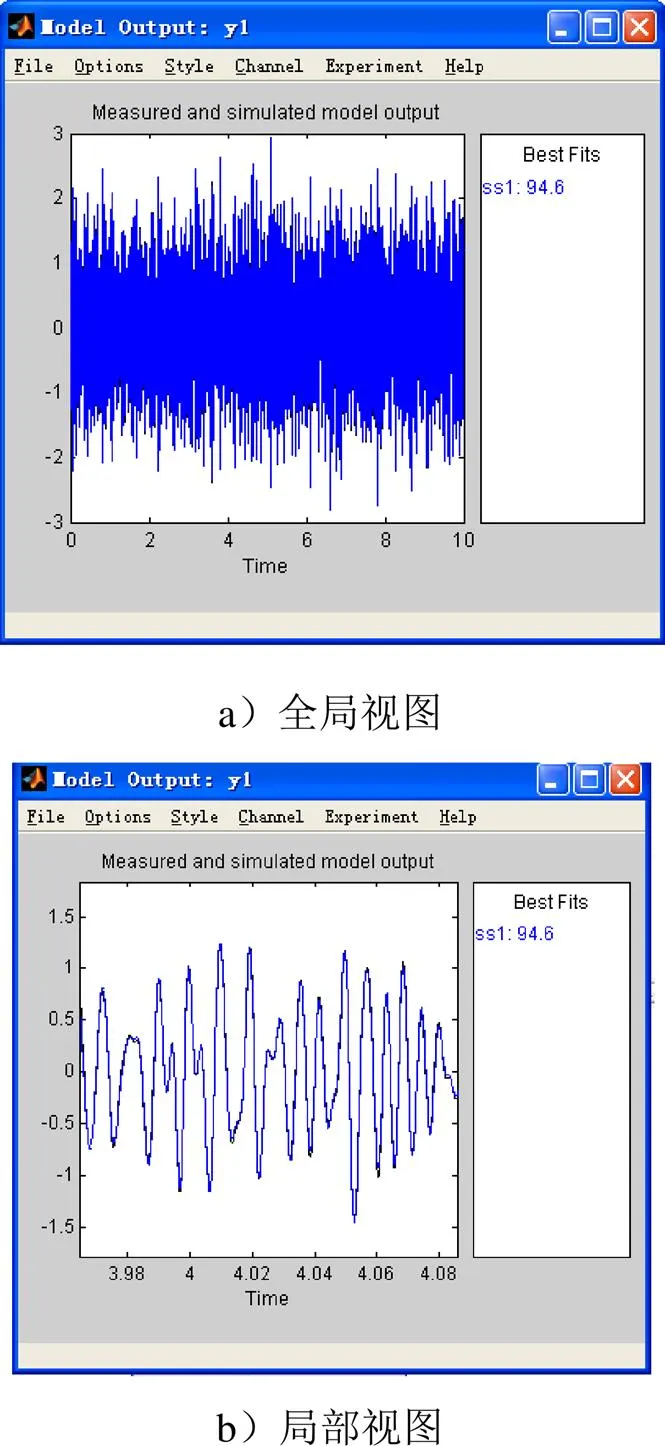
图11 模型预测对比

控制参数选用收敛系数=0.01，泄露系数=0.995，分别对120Hz、130Hz、150Hz、160Hz、170Hz正弦信号、100Hz～500Hz宽频信号进行了控制，结果如下所示，降噪效果明显，正弦信号降低超过6dB，宽频噪声环境降低3dB。

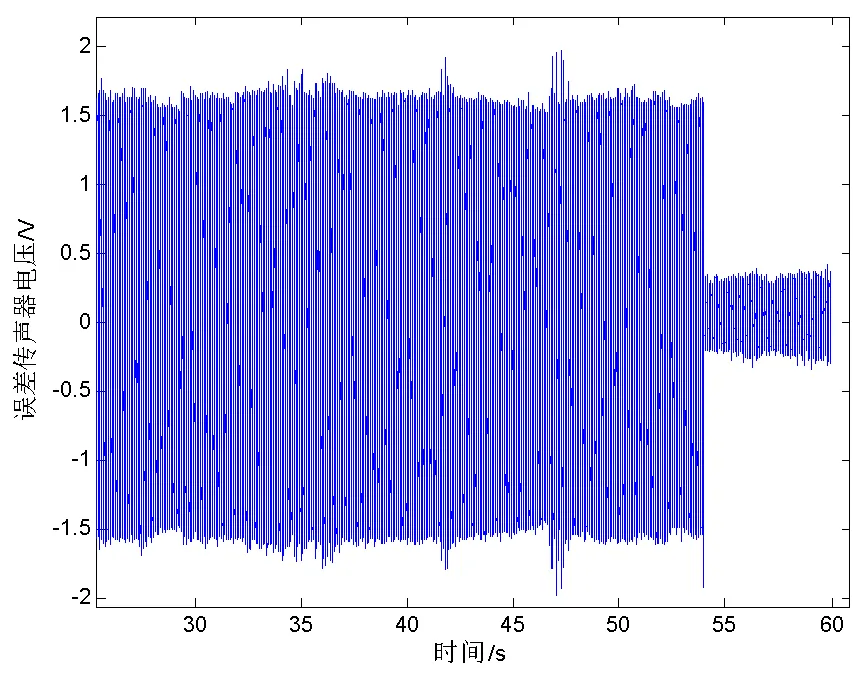
图12 正弦信号控制效果

图13 随机信号控制效果

2.2 多通道MIMO控制（2通道）

多通道MIMO控制如图14所示。

1-控制扬声器*2，2-噪声源音响*6，3-误差传声器*2，4、5、6-声场测量传声器

2个次级扬声器同向布置、音响与扬声器相对布置，其中噪声源1-1与误差传声器3-1相对，二者间次级通道设为原点传递11，同理得到1-2与3-2之间原点传递为22，1-1与3-2之间跨点传递12，1-2与3-1之间跨点传递为12。辨识采用单输入多输出辨识，通过两次辨识试验，获得上述4个次级通道模型。

通过现场调试发现，控制效果受原点传递H(=)参数影响较大，原点传递收敛系数=0.01，泄露系数均为a=0.995，分别以170Hz正弦信号、100Hz～500Hz宽频随机信号作为噪声源开展噪声主动控制，结果如下所示，降噪效果明显，正弦信号降低6dB以上，宽频噪声环境降低3dB以上。

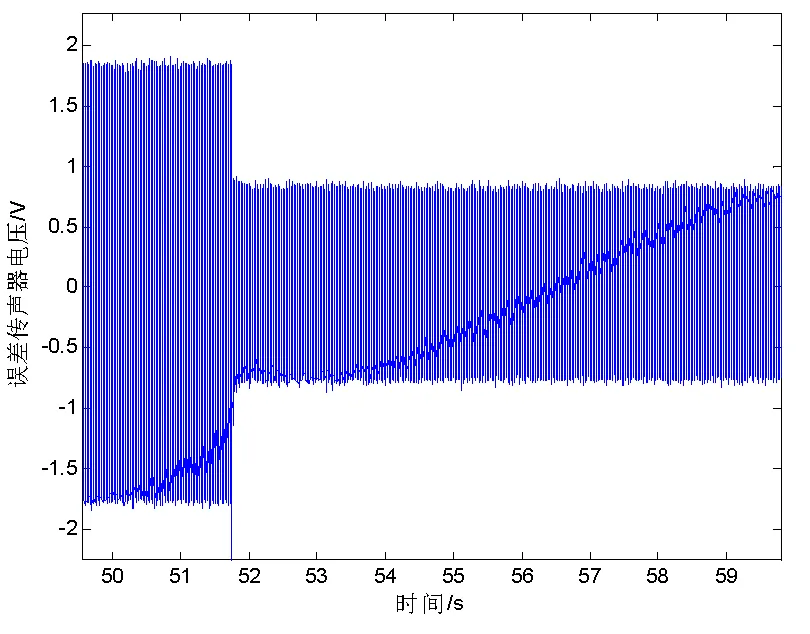
图15 正弦信号控制（3-1处声压）

图16 正弦信号控制（3-2处声压）

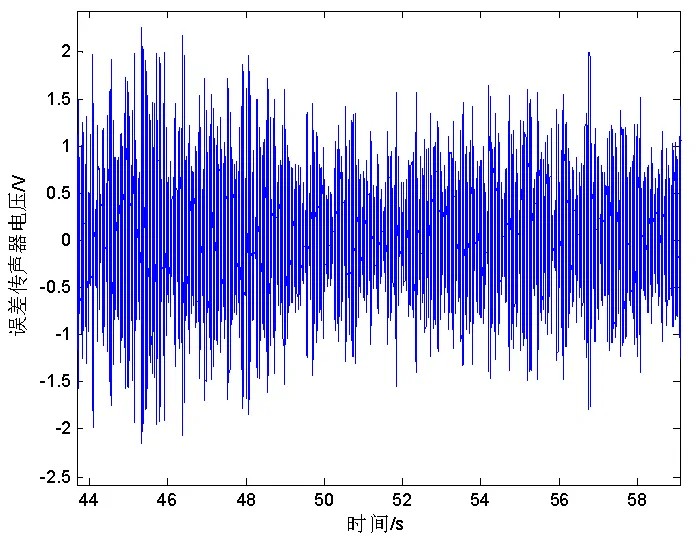
图17 随机信号控制（3-1处声压）

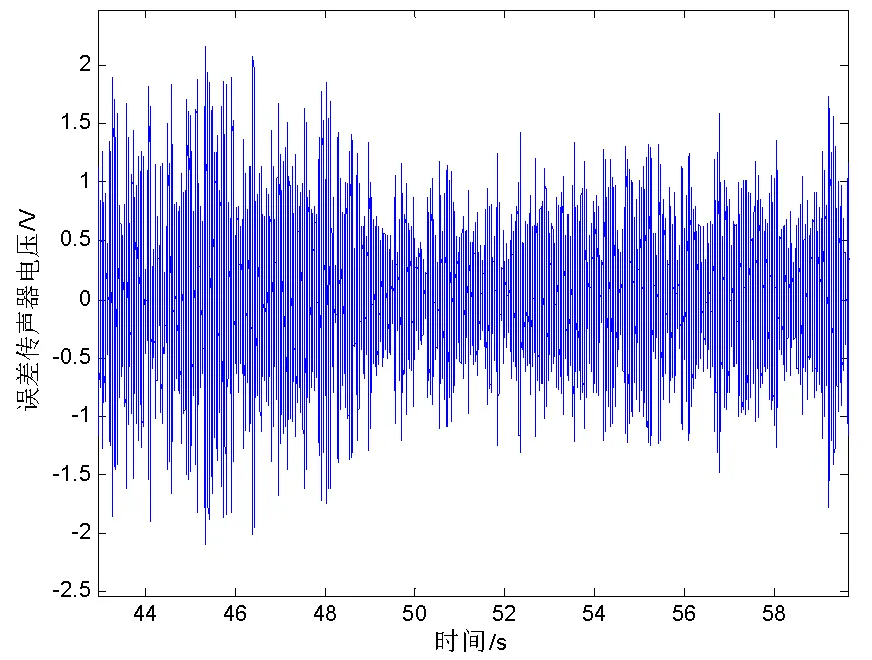
图18 随机信号控制（3-2处声压）

3 密闭空间噪声主动控制试验验证

圆筒内噪声主动控制采用MIMO控制，扬声器位于筒底部，将传声器安置于横梁支架上，分别与1、2次级扬声器对应，如图19所示。试验系统如图20所示。

1-控制扬声器*2，2-误差传声器*2

图20 密闭空间声主动控制试验

圆筒内噪声主动控制结果如图21、图22所示，分别对170Hz正弦信号、100Hz～500Hz宽频信号进行了控制，与自由空间MIMO控制结果相比，内声场信号已经不是纯正弦或宽频随机信号，在激励频率信号的基础上受到声辐射的干扰，将控制信号在控制频率范围内滤波进行分析，发现基于Fx-LMS的多通道MIMO控制方法降噪效果依然显著，舱内噪声正弦信号由128dB降为121dB，降低超过6dB，宽频噪声信号由128dB降为124dB，降低超过3dB。

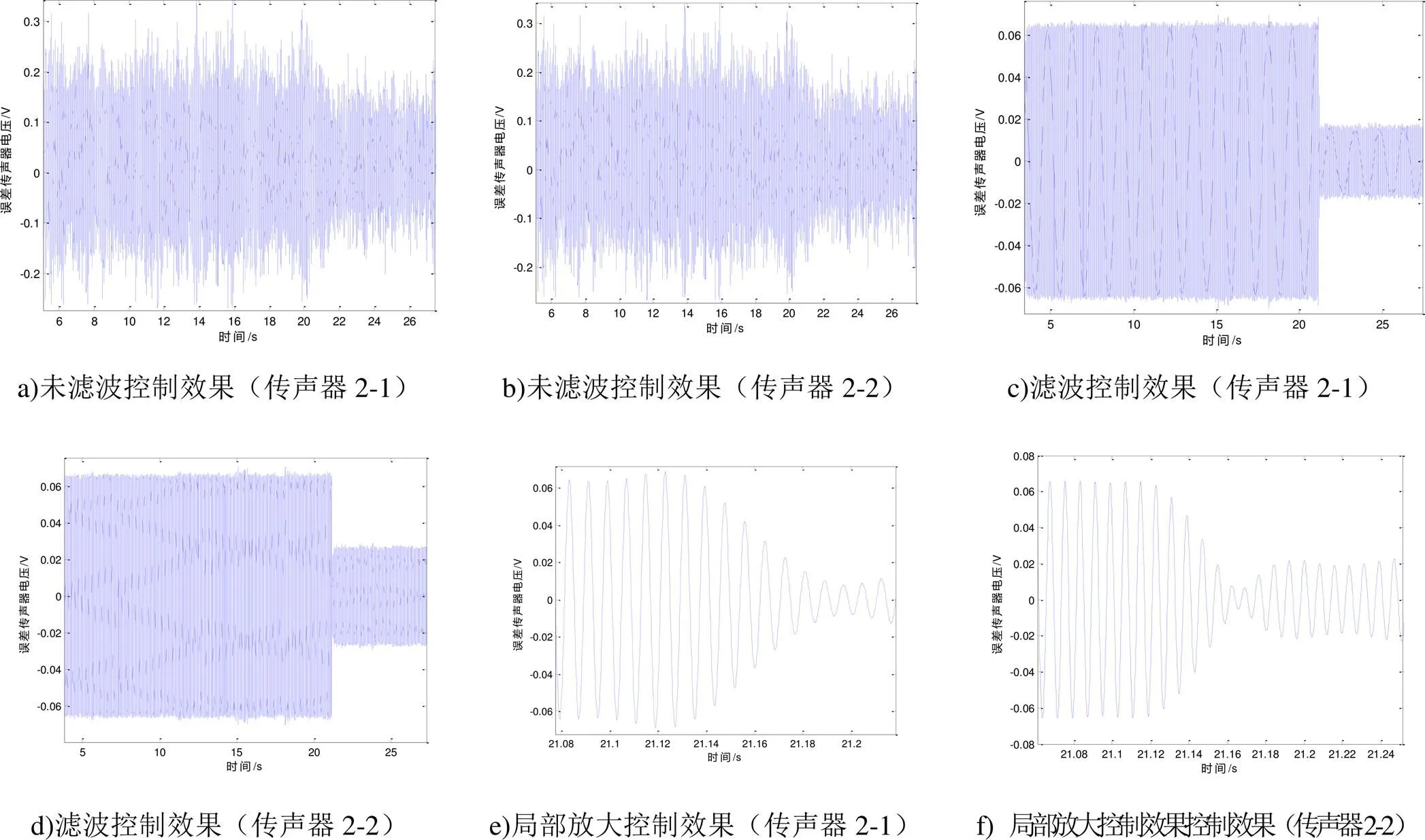
图21 正弦信号控制效果

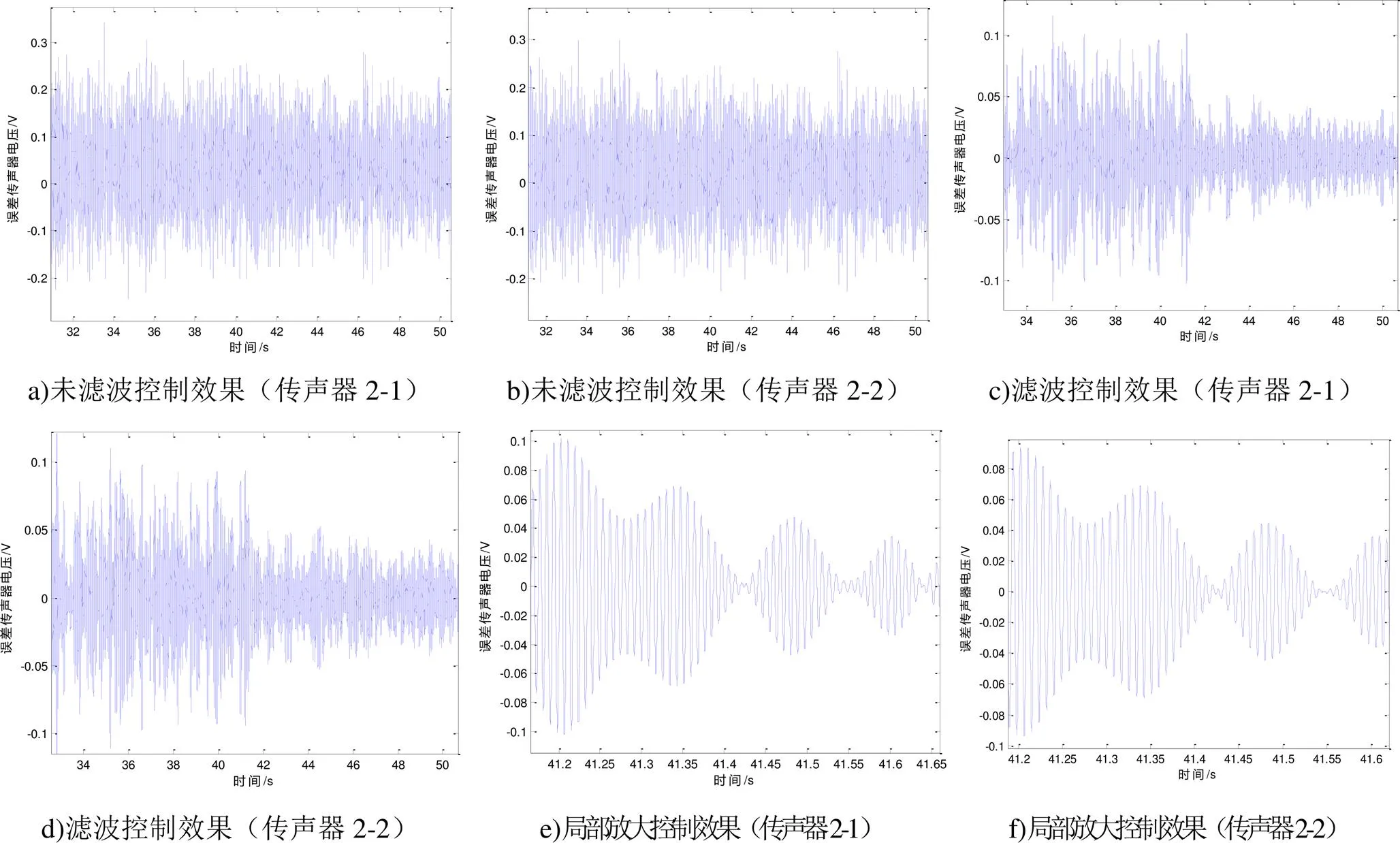
图22 随机信号控制效果

4 结论

本文针对多通道Fx-LMS算法进行了改进，提出一种可工程应用的多通道噪声主动控制算法，具体改进包括：1)对离散状态空间方程模型进行改进，使之具备并行计算多组响应的能力。2)增加了权系数锁定开关，在自适应权系数收敛后，可将其锁定为常值，从而增加了控制系统的稳定性。3)对算法整体进行了优化，使得改变少量参数，即可适用于不同噪声源数、控制扬声器数和噪声控制点数的噪声主动控制问题。4)本控制算法中大多数参数方便调节，因此，为多通道噪声主动控制的试验研究提供了便利条件。利用改进的控制算法开展了从单通道到多通道、从自由声场到密闭空间、从正弦噪声到随机噪声等一系列噪声主动控制试验，试验验证了该算法的有效性。

控制系统的控制参数（学习率、泄漏因子等）直接影响控制系统的稳定性、控制精度以及收敛速度，目前这些参数主要凭经验设置，通过手动调试获得合适参数值。但对于多通道控制系统而言，次级通道的增加导致控制参数增多，任何一个参数值不合理，都有可能影响控制的精度，甚至导致系统发散。因此对于多通道噪声主动控制系统，如何有效设置多个控制参数，将是后续研究的主要问题。

[1] 朱从云, 赵则祥, 李春广, 等. 噪声控制研究进展与展望[J]. 噪声与振动控制, 2007, (3): 1-8, 19. [Zhu Congyun, Zhao Zexiang, Li Chunguang, et al. Development and prospect of noise control research [J]. Noise and Vibration Control, 2007 (3): 1-8,19.]

[2] 任方, 张正平, 李海波, 等. 基于吸声材料的火箭整流罩噪声环境控制[J]. 固体火箭技术, 2016(6): 851-856. [Ren Fang, Zhang Zhengping, Li Haibo, et al. Noise control technology of launch vehicle fairing using sound-absorbing material [J]. Journal of Solid Rocket Technology, 2016(6): 851-856.]

[3] Lueg P. Process of silencing sound oscillation[P]. US. Patent 2043, 416: 1936.

[4] 齐江龙, 原凯, 陈雅曦, 等. 运载火箭整流罩降噪技术研究进展[J]. 导弹与航天运载技术, 2019, 39(4): 119-123. [Qi Jiang-long, Yuan Kai, Chen Yaxi, et al. Research progress on noise attenuation technology of launch vehicle fairing[J]. Missiles and Space Vehicles, 2019, 39(4): 119-123.]

[5] 常振臣, 王登峰, 周淑辉, 等. 车内噪声控制技术研究现状及展望[J]. 吉林工业大学学报(工学版), 2002, 32(4): 86-90.[Chang Zhenchen, Wang Dengfeng, Zhou Shuhui, et al. Research developments and prospects of noise control technology in vehicle [J]. Journal of Jilin University of Technology, 2002, 32(4): 86-90.]

[6] 闾晨光. 舰艇动力装置主动噪声控制技术研究[J]. 科技创新导报, 2014, 31: 50. [LV Chenguang. Research on active noise control technology of ship power plant [J]. Science and Technology Innovation Herald, 2014, 31: 50.]

[7] 陈磊. 数字信号处理技术在噪声频谱分析仪中的应用[D]. 西安电子科技大学, 2010.

[8] 刘日山. 封闭空间噪声自适应有源控制的研究[D]. 福建农林大学, 2009.

[9] 陈克安, 马远良. 自适应有源噪声控制——原理、算法及实现[M]. 西安: 西北工业大学出版社, 1993.

[10] Kuo SM, Kong X, GanWS. Applications of adaptive feedback active noise control system[J]. IEEE Transactions on Control Systems Technology, 2003, 11: 216-220.

[11] 赵斌. 自适应逆控制及其在有源噪声控制中的应用[D]. 燕山大学, 2002.

[12] 陈端石, 关元洪. 噪声主动控制研究的发展与动向[J]. 应用声学, 2001, 20(4): 1-5. [Chen Duanshi, Guan Yuanhong. Development of active noise control [J]. Applied Acoustics, 2001, 20(4): 1-5.]

Experiment of Active Noise Reduction Based on Multi-Channel Adaptive Filtering Algorithm

GAO Bo ZHANG Zhong WEI Long HOU Chuan-tao REN Fang QIN Zhao-hong GUO Jing

(Beijing Institute of Structure and Environment Engineering, Science and Technology on Reliability and Environmental Engineering Laboratory, Beijing 100076,China)

FXLMS adaptive control algorithm is widely used in active noise control because of its small amount of computation, easy implementation and clear physical mechanism. At present, the application cases of active noise control in engineering mainly use single channel noise active control algorithm. Compared with single channel control algorithm, multi-channel control algorithm has better control effect, but it is less applied in engineering due to its complex structure. Therefore, this paper improves the multi-channel adaptive filtering algorithm and verifies its effectiveness through experiments, which provides a feasible scheme for the engineering application of multi-channel noise active control system.

Active noise control; Multichannel FXLMS algorithm; Discrete state space equation; Leakage factor

V414

A

1006-3919(2022)03-0028-08

10.19447/j.cnki.11-1773/v.2022.03.005

2021-12-20；

2022-04-11

科技部国家重点研发计划（2021YFB3801700）;重点实验室基金（6142911180512）

高博（1992—），男，硕士，工程师，研究方向：动力学与控制；（100076）北京9200信箱72分箱.