考虑扭曲和膨胀耦合效应的复合材料基体细观失效准则研究

刘准 卞亚东 谭日明 赵曜 王聪伟

考虑扭曲和膨胀耦合效应的复合材料基体细观失效准则研究

刘准1卞亚东1谭日明2赵曜1王聪伟1

（1 中国运载火箭技术研究院，北京，100076；2 北京航天发射技术研究所，北京，100076）

为了更准确地表征基体扭曲和膨胀对复合材料失效的耦合影响，本文对跨尺度分析中的失效准则进行了改进。建立了代表不同纤维排布规律的单胞模型，并基于单向板试验数据，确定了T300/5228A复合材料组分的失效临界参数，说明了铺层角度较小时，单层内基体失效由扭曲主导，铺层角度增大，基体失效向膨胀主导转变。最后，对开孔层合板压缩进行了跨尺度分析，验证了本文失效定义方法及模型的有效性。

细观失效；复合材料；基体；扭曲；膨胀

0 引言

碳纤维增强树脂基复合材料具有比强度和比刚度高、可设计性好等优点，其使用量已经成为衡量现代飞行器结构先进性的重要标志[1]。仿真分析时，针对复合材料单层级的宏观方法计算效率较高，建立复杂结构模型相对容易，广泛应用在工程计算中[2]，但失效行为仅能根据单层级应力/应变定义。组分级的全尺寸细观模型对材料力学性能及失效行为的表征更加直接，但计算量巨大，很难在工程上推广。近年来，跨尺度分析方法逐渐发展起来，其核心是宏/细观应力/应变的转换和组分级的失效定义，该方法能够兼顾宏观模型的计算效率和细观模型的分析精度，是一种很有潜力的仿真手段[3-4]。

基于跨尺度分析方法，Iwai等人对复合材料长期寿命进行了研究[5]，Low等人对复合材料低速冲击失效机理进行了研究[6]，Li等人提出了一种基于细观应力的失效准则，并将其应用在开孔层合板拉伸失效分析中[7]，本人在此基础上，对不同偏轴角度的单向板力学性能进行了系统研究[8]。这些研究均表明了跨尺度分析方法在复合材料失效分析中的适用性和先进性。

为了表征复合材料组分在复杂应力状态下的失效行为，本文提出一种基于细观应力的基体失效准则。结合单胞模型，对准则中失效临界参数的确定方法进行研究，并建立T300/5228A开孔层合板跨尺度分析模型，结合试验数据进行对比分析。

1 跨尺度分析方法

基于细观应力的复合材料跨尺度分析可以概括为三个步骤：1）计算复合材料单层级宏观应力状态；2）将单层级宏观应力转换为纤维和基体中组分级细观应力；3）根据细观应力进行组分级失效定义。其中，复合材料宏观/细观应力转换是分析过程中的关键，通过定义放大矩阵建立对应关系，具体为

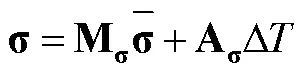
2 细观失效准则

在跨尺度分析中，通过公式（1）将单层级宏观应力转换为对应的组分级细观应力，利用细观失效准则对纤维和基体失效进行直接定义。其中，纤维失效可采用组分级最大应力准则定义[8]，而树脂基体为各向同性材料，却有不同的拉伸和压缩强度，这说明基体失效不仅和von-Mises等效应力sVM有关，还受体积应力不变量1的影响。基于此，不同学者提出了公式（2）中不同形式的基体失效准则。

Ha等人[9]提出了MMF（Micro-mechanics failure）失效准则，Raghava等人[10]和Bauwens[11]考虑了不变量间对基体失效不同程度的耦合影响，分别提出了von-Mises失效准则的改进形式。Sign等人[12]考虑了基体剪切性能和拉伸、压缩性能对失效的耦合影响，提出了有3个强度参数的MMF失效准则。对于树脂基体，拉伸、压缩性能主导了其抵抗膨胀失效的能力，剪切性能则主导了其抵抗扭曲失效的能力，3参数MMF失效准则本质上是考虑了基体扭曲和膨胀对失效的耦合影响。

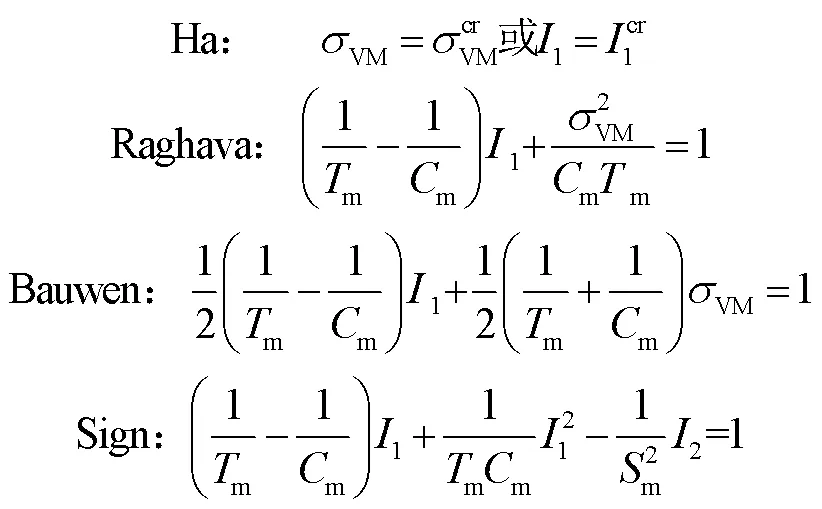
借鉴Sign等人修正失效准则的思想，本文提出公式（3）形式的工程化基体失效准则，当基体应力满足公式（3）时，出现损伤起始

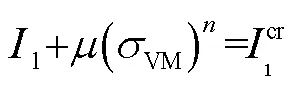
3 代表体积单元

公式（1）中机械应力放大矩阵和热应力放大矩阵可借助复合材料代表体积单元有限元模型（单胞模型）确定，考虑典型的纤维排布，本文建立三种单胞模型（正方形、六边形、钻石形），见图1。为了能够覆盖到纤维和基体中不同位置的损伤起始，在单胞模型中关键位置设置参考点，求得对应的应力放大矩阵，建立起宏观模型积分点处宏观应力状态和单胞模型不同参考点处细观应力状态的对应关系。

承载过程中，复合材料内每个代表体积单元具有相同的形变，相邻的代表体积单元没有分开或者重合以保证材料的连续性。由此，建立的单胞模型均采用周期性边界条件[13, 14]，即两个相对边界平面上成对的节点位移有如下关系

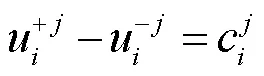
式中，代表了法向为j方向的边界平面上的一个节点沿着i方向的位移和为两个相对平面上的对应的一对节点位移，为常数，通过对单胞模型施加周期性边界条件，保证所有相对边界上的成对节点在相同方向上具有相同的位移。

4 应用与讨论

4.1 失效临界参数拟合

本文建立的基体细观失效准则考虑了扭曲和膨胀对其失效的耦合影响。对于承受不同偏轴角度载荷的复合材料单向板，其基体处于不同比例的多轴应力状态，扭曲和膨胀共同导致了基体失效。由此，根据单向板不同角度的偏轴强度来确定基体细观失效临界值能够更准确的定义基体失效行为。作者在文献[8]中针对典型复合材料T300/5228A单向板进行了不同偏轴角度的拉伸、压缩试验，结果见表1，随着偏轴角度的增大，强度逐渐降低。

当单向板承受角度为的偏轴载荷时，载荷坐标系绕Z轴旋转角度得到单向板宏观材料坐标系，见图 2，绕Z轴对应力边界进行转换，得到材料坐标系下的宏观应力状态。

表1 单向板偏轴试验结果

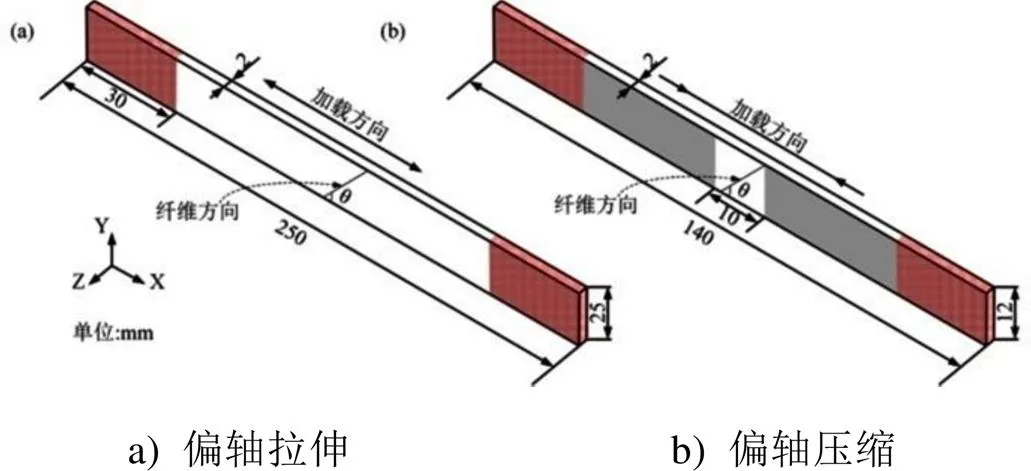
图2 复合材料单向板偏轴受载示意图

相对于单向板宏观材料坐标系，考虑代表体积单元细观材料坐标系在2-3平面内的随机性，将其绕1轴旋转任意角度，见图 3，将应力状态转换为单胞模型的力学边界条件。根据先后绕3轴、1轴旋转的坐标系转换公式，可得到偏轴角度时，单向板宏观应力边界和单胞模型应力边界的对应关系，见公式（5）。

图3 2-3平面内代表体积单元选取示意图

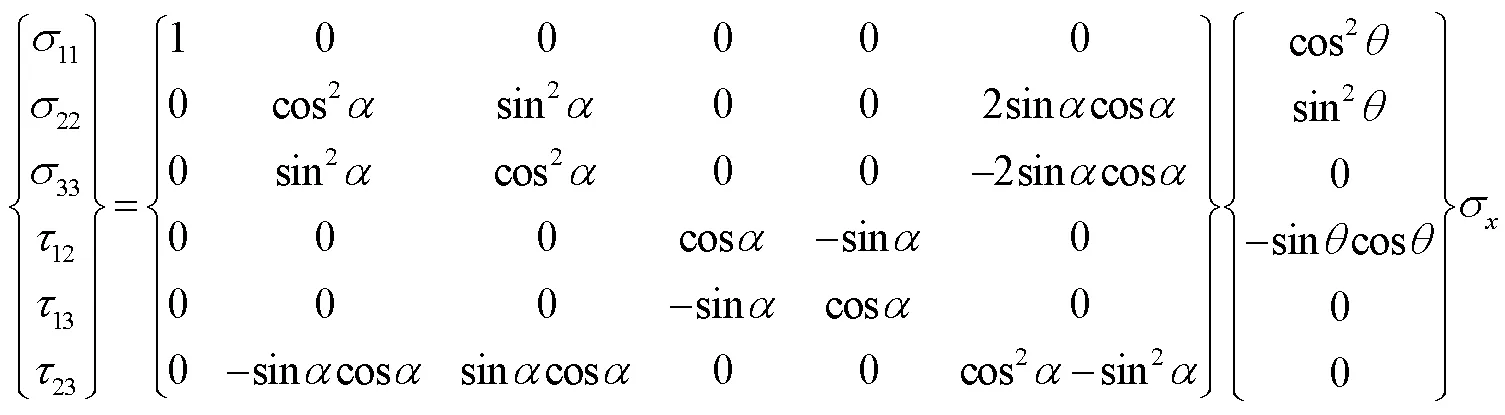
式中，σ为单向板偏轴受载的应力边界，当其等于偏轴强度时，求得的单胞模型应力边界即为基体失效时代表体积单元的受载状态，此时，基体中一个或多个参考点处的第一应力不变量1和von Mises等效应力svm满足公式（3），对应的单向板宏观模型积分点处发生了基体失效，据此可确定基体失效临界值。具体地，将根据公式（4）和单向板偏轴拉/压强度所确定的边界条件施加到3种单胞模型中，得到模型内第一应力不变量1和von Mises等效应力svm的分布。将单胞模型中积分点处的1和（svm）分布在直角坐标系中，数据边界应满足公式（3），即可通过最佳线性拟合确定5228A树脂基体适用的指数和对应的失效临界参数。=2时，3种单胞模型的计算结果见图4，2条直线确定了单胞模型在不同偏轴角度下的失效边界。当积分点上的（1，（svm）2）处在2条直线及坐标轴所围成的区域内部时，基体完好；当积分点上的（1，（svm）2）处在2条直线上时，该积分点处出现损伤。由此确定了基体失效准则

图4 基体细观失效参数拟合

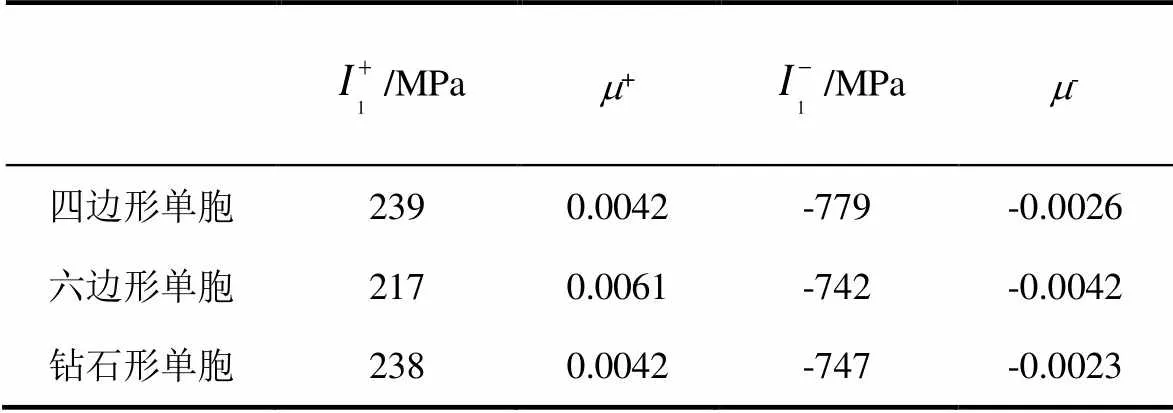
表2 基体5228A细观失效准则参数拟合结果

4.2 层合板跨尺度分析

针对铺层为[45/0/-45/90]4s的复合材料T300/5228A开孔层合板建立跨尺度分析有限元模型，结合本文提出的细观失效准则，对其压缩强度进行计算，并与文献[15]中试验结果进行对比。跨尺度分析模型原理如图5所示，仅对称截取开孔层合板54 mm长的一段建立模型以提高计算效率。模型利用ABAQUS建立，包含32个单层，使用实体单元C3D8R，利用本文提出的细观失效准则对基体进行失效定义，纤维失效定义和损伤演化方法参考文献[8]，整个分析流程通过编写子程序VUMAT实现。

图6所示为载荷最大时刻对应的层内损伤状态，在主承载的0°层内，孔边截面出现了横向贯穿损伤，在45°层内，由于剪切应力的作用，出现了非对称的基体损伤。下一时刻载荷突降超过了30%，开孔层合板整体失效。根据破坏载荷确定试验和计算的开孔层合板压缩强度分别为322.9MPa和309.0MPa。

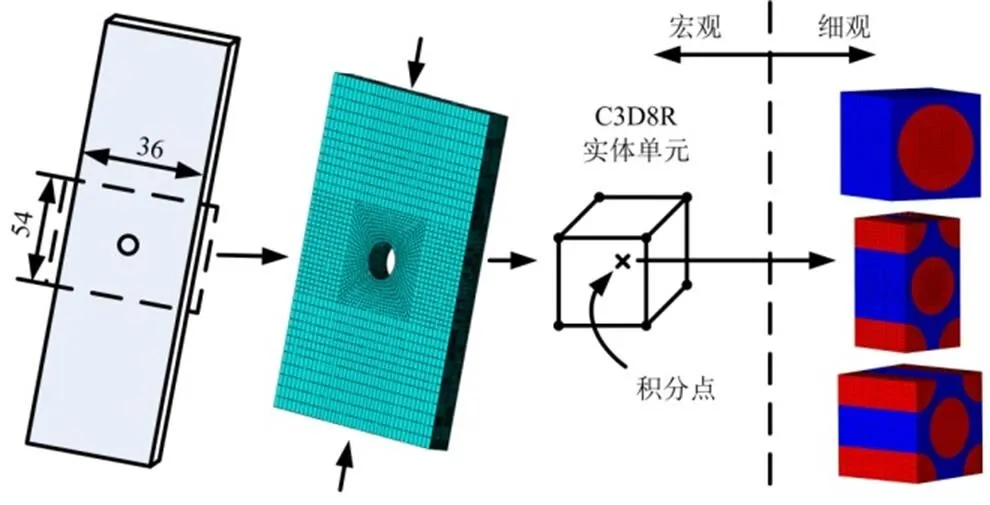
图5 开孔层合板压缩跨尺度分析

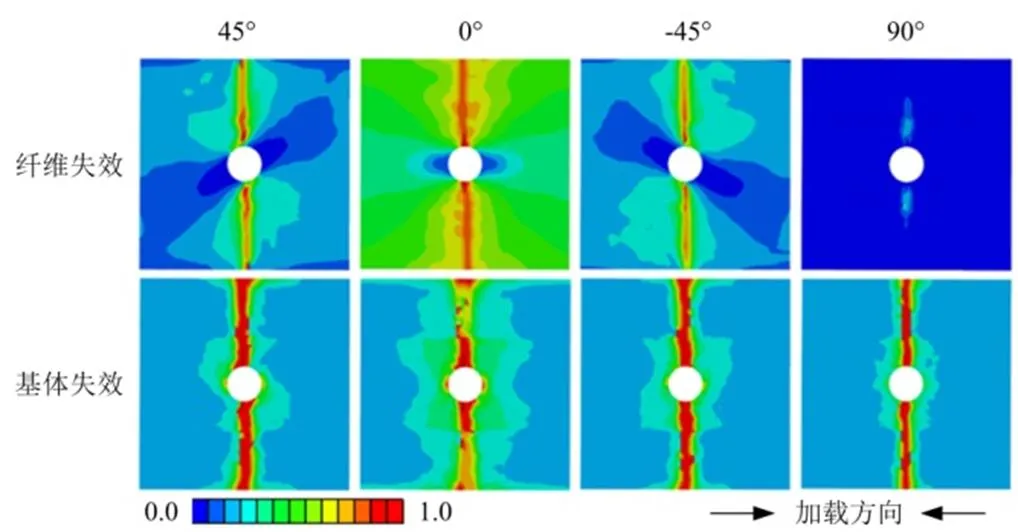
图6 最大载荷时刻层合板损伤情况

文献[15]研究表明，相较聚集铺层[454/04/-454/904]s，单层更薄的离散铺层[45/0/-45/90]4s开孔层合板相同厚度下层数更多，损伤容限性能更好，即在宏观上具有更长的损伤过程和更高的强度。本文模型虽然考虑了基体扭曲和膨胀的耦合，但未充分表征纤维/树脂界面的细观渐进损伤[16]、单层间的宏观渐进损伤及单层内纤维失效模式（扭结或脆断）对层合板损伤过程和强度的影响，导致预测强度偏低约4.3%。

5 结论

本文提出了一种基于细观应力的基体失效准则，建立了代表不同纤维排布规律的单胞模型，并考虑了其在2-3平面内选取的随机性。根据确定的模型参数，对开孔层合板压缩进行了跨尺度分析，并与试验数据进行对比研究。主要结论如下：

1）将单向板不同方向的偏轴强度转化为单胞模型的力学边界条件，对积分点处（1，(svm)）进行线性拟合，结果说明铺层角度较小时，单层内基体发生svm主导的扭曲失效，铺层角度增大，基体失效向1主导的膨胀失效转变。

2）对比开孔层合板压缩的跨尺度分析和试验结果，两者吻合较好，说明了细观失效准则及确定的失效临界参数能够有效表征复合材料组分失效行为，验证了模型的有效性。

[1] 马征. 国外下一代战斗机和高超声速飞机结构技术发展综述[J]. 强度与环境, 2021, 48(5): 15-21. [Ma Zheng. Overview of the structural technology development of foreign next-generation fighters and hypersonic aircraft[J]. Structure & Environment Engineering, 2021, 48(5): 15-21.]

[2] 姜封国, 裴廷瑞, 姜旭宏, 等. 复合材料加筋板高速冲击的损伤研究[J]. 强度与环境, 2021, 48(4): 12-17. [Jiang Fengguo, PEI Tingrui, Jiang Xuhong, et al. Study on damage of composite stiffened board under high-velocity impact [J]. Structure & Environment Engineering, 2021, 48(4): 12-17.]

[3] Jin K K, Huang Y, Lee Y H, et al. Distribution of micro stresses and interfacial tractions in unidirectional composites[J]. Journal of Composite Materials, 2008, 42(18): 1825-1849.

[4] Ha S K, Huang Y, Han H H, et al. Micromechanics of failure for ultimate strength predictions of composite laminates [J]. Journal of Composite Materials, 2010, 44(20): 2347-2361.

[5] Iwai K, Cai H, Nakada M, et al. Prediction of long-term fatigue strength of quasi-isotropic CFRP Laminates with a hole under compressive loading[J]. Science and Engineering of Composite Materials, 2010, 17(4): 227-241.

[6] Lou X, Cai H, Yu P, et al. Failure analysis of composite laminate under low-velocity impact based on micromechanics of failure [J]. Composite Structures, 2017, 163: 238-247.

[7] Li X, Guan Z D, Li Z S, et al. A new stress-based multi-scale failure criterion of composites and its validation in open hole tension tests[J]. Chin. J. Aeronaut. 2014, 27: 1430-1441.

[8] Liu Z, Guan Z D, Tan R M, et al. Multi-scale analysis of CFRP laminates with MMF3 criterion under different off-axis loading conditions, Materials , 2018, 11(11): 1-11.

[9] Ha S K, Jin K K, Huang Y. Micro-mechanics of failure (MMF) for continuous fiber reinforced composites [J]. Journal of Composite Materials, 2008, 42(18): 1873-1895.

[10] Raghava R, Caddell R M, Yeh G S Y. The macroscopic yield behaviour of polymers [J]. Journal of Materials Science, 1973, 8(2): 225-232.

[11] Bauwens. Yield condition and propagation of Luders’ lines in tension-torsion experiments on Poly (Vinyl Chloride) [J]. Journal of polymer science part a-2: polymer physics, 1970, 8(6): 893-901.

[12] Tsai S W. Strength & life of composites [M]. Composites Design Group, Department of Aeronautics & Astronautics, Stanford University, 2008: 6-29-6-51.

[13] Bouaoune L, Brunet Y, Moumen A E, et al. Random versus periodic microstructures for elasticity of fibers reinforced composites [J]. Composites Part B Engineering, 2016, 103:68-73.

[14] Zhang Y, Ellyin F, Xia Z. An unified periodical boundary conditions for representative volume elements of composites and applications [J]. International Journal of Solids and Structures, 2003, 40(8): 1907-1921.

[15] 刘准, 关志东, 黎增山, 等. 考虑时间和温度影响的复合材料开孔层板压缩失效分析[J]. 复合材料学报, 2017, 34(7): 1489-1495. [Liu Zhun, Guan Zhidong, Li Zengshan, et al. Time-temperature dependent failure analysis of open-hole composite laminates under compression loading[J]. Acta Materiae Composite Sinica, 2017, 34(7): 1489-1495.]

[16] 张叶凡, 梁耕源, 尹昌萍, 等. 纤维增强树脂基复合材料界面相容性研究现状[J]. 强度与环境, 2020, 47(3): 43-50. [Zhang Yefan, Liang Gengyuan, Yin Changping, et al. A Review on the interfacial compatibility of fiber reinforced resin matrix composites [J]. Structure & Environment Engineering, 2020, 47(3): 43-50.]

Research on the Micro-Mechanics Failure Criterion of CFRP Considering Coupling Effect of Matrix Distortion and Dilatation

LIU Zhun1BIAN Ya-dong1TAN Ri-ming2ZHAO Yao1WANG Cong-wei1

(1 China Academy of Launch Vehicle Technology, Beijing, 100076,China; 2 Beijing Institute of Space Launch Technology, Beijing, 100076,China)

Aiming to better explain coupling effect of matrix distortion and dilatation, the micro-mechanics failure criterion in multi-scale analysis of CFRP was modified. Representative volume element (RVE) models of three typical distributions of fiber and matrix were built. Based on the RVE models and test data of unidirectional laminates, critical values of T300/5228A constituents were determined. Results show that the dominant factor of matrix failure tends to be distortion instead of dilatation as ply angles increase. Furthermore, The failure of open-hole laminates under compression was studied with established multi-scale model, and the definition method of micro failure was verified.

Micro-mechanics failure; CFRP; Matrix; Distortion; Dilatation

TB332,V417+.4

A

1006-3919(2022)03-0008-06

10.19447/j.cnki.11-1773/v.2022.03.002

2021-09-13；

2022-02-19

国家重点基础研究发展计划(973计划)资助项目(2010CB631103)

刘准（1991—），男，工程师，研究方向：复合材料结构设计；（100076）北京9200信箱1分箱-1.