固体火箭发动机燃烧室轴向平均流速对声模态影响研究

刘陆广 侯凯宇 史晓鸣 夏鹏 李海东 高阳 李海波

固体火箭发动机燃烧室轴向平均流速对声模态影响研究

刘陆广1侯凯宇2史晓鸣1夏鹏1李海东1高阳1李海波3

（1上海机电工程研究所，上海，201109；2 上海航天技术研究院，上海，201109；3 北京强度环境研究所，北京，100076）

固体火箭发动机不稳定燃烧与发动机燃烧室声模态特性密切相关，降低燃烧室声模态频率与涡脱落频率之间的涡声耦合程度可以大大降低固体火箭发动机不稳定燃烧发生的概率。然而，目前关于发动机燃烧室声模态特性研究主要基于燃烧室内燃气介质静止状态，而没有考虑固体火箭发动机实际工作中燃气介质的流动特性。本文以大长径比固体火箭发动机不稳定燃烧现象为背景，通过理论推导与数值计算相结合的方法研究轴向平均流速对燃烧室模态频率的影响机理。研究结果表明，平均流速的存在不仅产生附加刚度项，而且产生系统附加阻尼项，从而改变了燃烧室声模态特性。

固体火箭发动机；不稳定燃烧；附加刚度；附加阻尼；平均流速

0 引言

随着导弹武器技术的发展，大推力、远射程军事需求的不断提高，固体发动机采用了大长径比、高装填、高能推进剂的设计。然而，在实际飞行过程中此类发动机容易出现燃烧不稳定，尤其是在工作末期。燃烧不稳定将造成固体火箭发动机推力及压强出现振荡，导致发动机壳体和其它构件振动，使飞行器可靠性降低，严重时将导致飞行任务失败[1-2]。目前，固体火箭发动机出现的不稳定大多属于轴向声不稳定，是推进剂燃烧室内流动过程和燃烧室声学特性共同作用的结果，成为了大长径比发动机研制过程中经常遇到的棘手问题之一[3-5]，其基本特征是燃烧室压力、燃速以发动机内燃烧室固有频率作周期或近似周期性的变化[6-9]，目前研究中通常将发动机燃烧室简化为一个封闭式容腔，采用声学方程描述压强振荡在容腔内传播和发展，针对该问题学术界目前开展了大量研究。

陈书明[10]等采用FE-SEA混合方法建立了燃烧室-平板-燃烧室混合模型，计算了在外部激励下燃烧室的响应声压级并与试验结果进行了对比，得到了典型平板的辐射效率；侯亮[11]等通过燃烧室结构耦合分析研究了机械结构的NVH问题，通过分析研究燃烧室及结构模态特性研究了工作噪声产生的机理，并给出了结构优化的指导意见；赵艳栋[12]等研究了双脉冲固体火箭发动机燃烧室压强振荡特性，重点关注了燃烧过程中燃烧室声振频率随燃面退移特性，研究结果表明：一级翼面装药燃烧室频率先减小后增大，二级内孔装药燃烧室频率则逐渐减小；杨向明[13]等研究了翼柱型装药固体火箭发动机燃烧室声场特性，建立了复杂装药结构固体火箭发动机燃烧室声场特性的计算模型，研究了有无喷管潜入段的翼柱型装药结构空腔的声振频率及小扰动频响特性，结果表明：不同位置扰动声压响应均出现在燃烧室固有频率段上；胡大宁[14]等研究了多种高装填、大长径比、翼柱型药柱固体火箭发动机不稳定燃烧现象，结果表明：不稳定燃烧取决于发动机的设计固有频率及发动机燃烧室内部声能的各种增益和衰减之间的消长关系，抑制不稳定燃烧的有效途径是改变燃烧室的固有频率和减少声能增益、增大声能损耗。秦朝红[15]等通过试验与仿真相结合的方式研究了声固耦合响应分析，得到了声场与结构场相互耦合效应下结构上的响应，以上研究结果表明，燃烧室声学特性是开展不稳定燃烧研究的基础。

然而，当前研究主要基于发动机内燃气介质静止状态开展，没有考虑真实发动机工作过程中内部燃气介质的流动特性，从而造成计算及试验结果较大的差距[13]。最近国内外研究学者开始关注发动机内燃气介质流动特性对燃烧室模态特性的影响，开展了一些理论方面的创新研究[16-19]。Vijaya[16]等采用WKB解分析研究了一维管道声腔考虑流速情况下的压力脉动特性，并将该分析结果应用到发动机不稳定燃烧问题，Wilson[17]采用曲线坐标系下特征值分析方法研究了平均流速下声学传递函数，Li[18]等基于WKB方法给出了环形燃烧声腔在平均流速概况下的解析解，并将该结果对欧拉数值解进行了对比，计算结果表明，低马赫数情况下解析解与数值解吻合较好，Saikumar[19]等采用半解析解方法研究了考虑平均流速情况下圆形管道的声学波动方程传播问题，计算结果表明，平均流速达到Ma=0.3情况时影响将非常明显，在平均流速较低情况下，静止状态与流动状态区别不大。真实固体火箭发动机工作过程中，非稳定燃烧通常发生在燃烧末端，此时，可以将发动机声腔等效为一维声腔，此时内部声场速度对系统动特性影响不可忽略因此，为了抑制大长径比固体火箭发动机不稳定燃烧问题，必须考虑发动机内燃气介质流动状态，给出考虑燃气介质流动状态下的燃烧室声模态特性，从而为精确抑制发动机不稳定燃烧提供数据支撑。本文通过理论推导及数值仿真相结合的方法研究了内部均匀流速对燃烧室声模态特性的影响。结果表明，平均流速的存在不仅改变了燃烧室声学系统的刚度特性，而且改变了系统的阻尼特性，从而改变了燃烧室声模态特性。

1 考虑平均流速控制方程推导

为了研究固体发动机燃烧介质流动对燃烧室模态特性的影响机理，将发动机燃烧室简化等效为一维圆柱结构，理论推导轴向流动速度对燃烧室模态特性的影响。

气体在管道内做一维流动，满足质量守恒连续方程

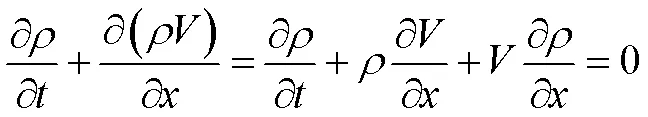
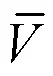
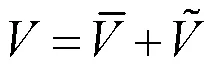
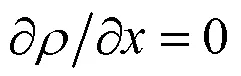
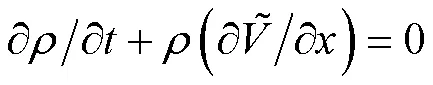
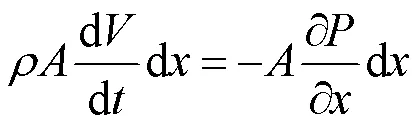
有轴向运动速度情况下，物质导数可以表示为式(5)

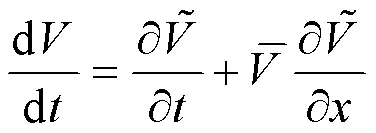
式(5)代入(4)得

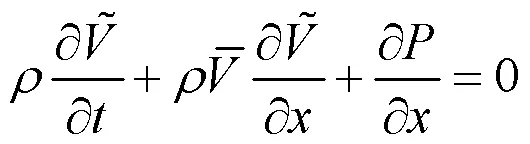
根据状态方程可以导出式（5）

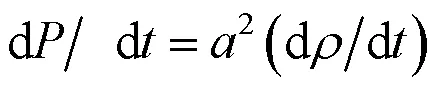
同理，在有轴向运动速度情况下，物质导数

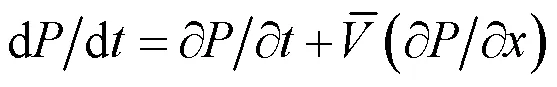
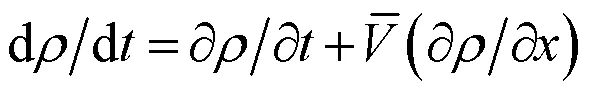
式(8)、(9)代入(7)得

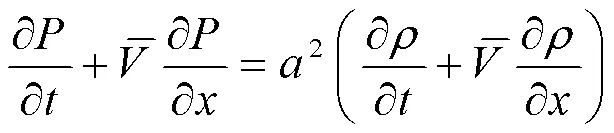
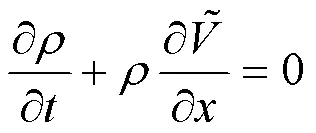
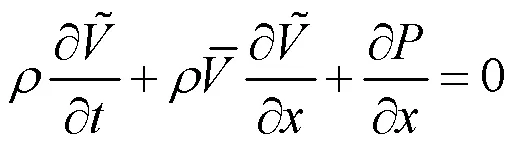
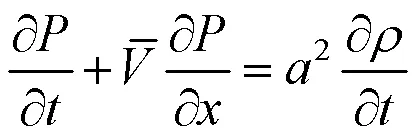
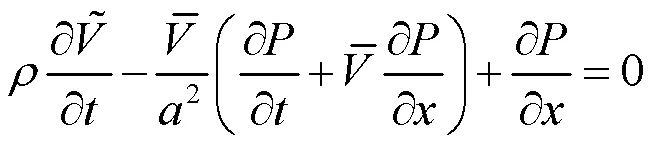
式(16)两边对求导得

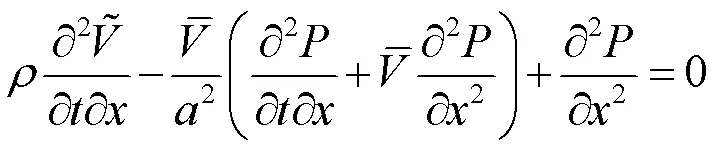
式(15)两边对求导得

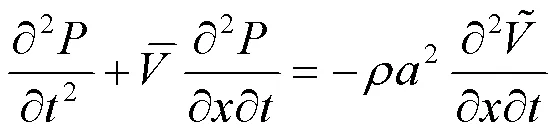
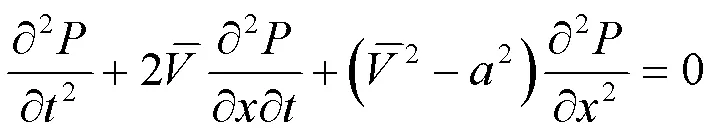
公式(19)即为考虑平均流速情况下一维声学控制方程。

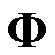
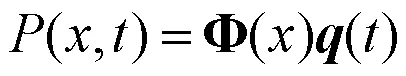
式中

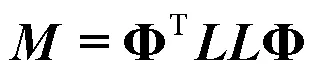
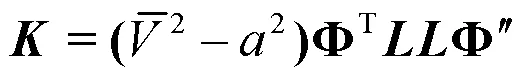
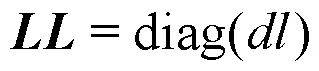
通过刚度矩阵及质量矩阵可以方便求解一维情况下考虑轴向平均流速时的燃烧室模态特性。根据以上推导结果可知，平均流速的存在不仅改变了燃烧室声学系统的刚度特性，而且改变了系统的阻尼特性，当平均流速达到当地声速时，燃烧室声学系统刚度将变为零，流速阻尼项与流速成2倍线性比例关系。

2 考虑平均流速效应差分求解

采用静止状态下满足边界条件的模态基函数对控制方程进行降阶求解。沿轴向状态均匀分为N个求解区域，N+1个差分节点。

根据获得的前10阶模态振型形成模态矩阵，实际求解中N取为30，沿轴向均分为30段，模态振型矩阵为30´10，采用泰勒展开生成振型矩阵的一阶导数及二阶导数矩阵。

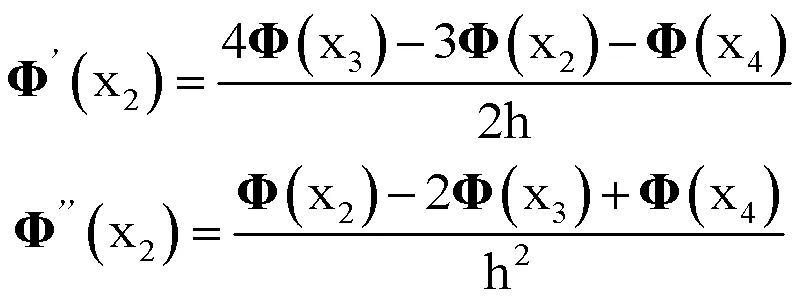
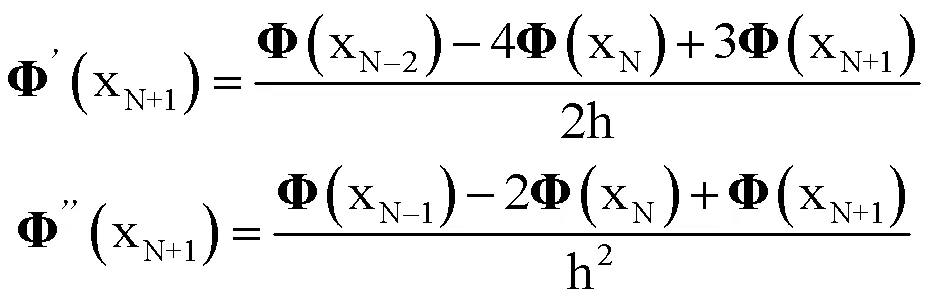
根据模态振型矩阵、一阶导数及二阶导数矩阵，通过左乘振型转置矩阵并沿轴向长度按单元划分积分求和从而形成对应的模态质量矩阵、模态刚度矩阵及模态阻尼矩阵。根据不同平均流速对阻尼及刚度的影响分析研究平均流速的存在对系统动特性的影响规律。

3 考虑平均流速效应试验研究

为研究平均流速对燃烧室声学系统模态特性的影响机理，首先开展了真实发动机声腔构型的试验研究，根据试验条件及能力研究了不同流速对真实发动机声腔模态频率的影响，考虑平均流速影响下的声腔模态测试系统如图1所示。

声模态测试系统组成如图2所示，声控制与采集仪产生电信号，经功率放大器后输入电动扬声器发声，激发燃烧室内的声学振荡，产生声场，采用传声器接收到的脉动压力信号，经传声器电源变换放大后输入到声控制与采集仪。在发动机声腔前后两端附近位置开设了气流加入装置及气流出口装置，用来产生流动声场。

图1 试验测试系统

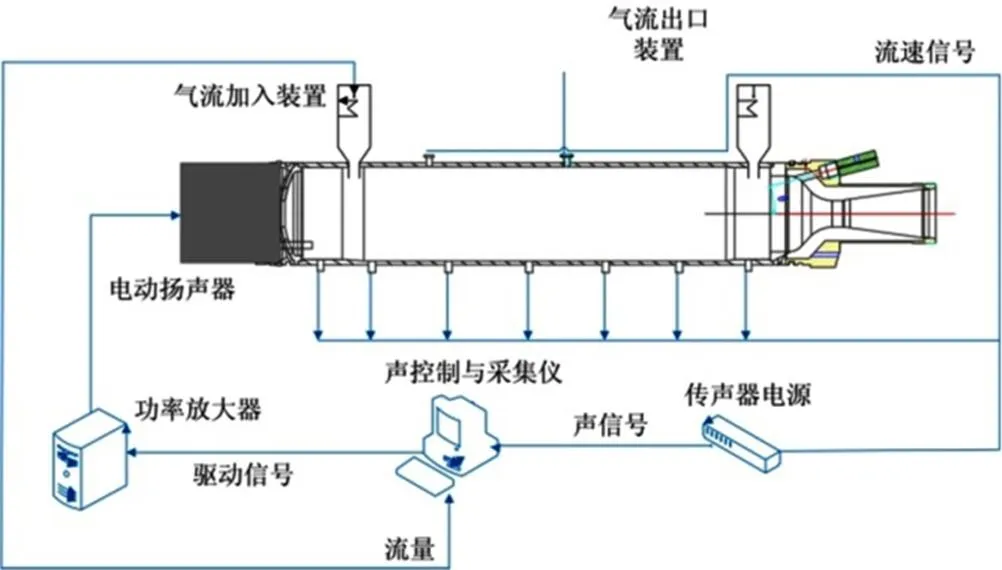
图2 试验测试原理图

传声器采用耐高温型传声器，可适用于后续高温下声场响应测试；在声腔轴线不同位置采用流速传感器测量加注情况下内部声腔气流速度，待流场稳定后开始测量。常温状态下，通过流量输入控制声腔内流速，依次使腔内流速达到几种不同速度0m/s、5m/s、10m/s、15m/s、20m/s及25m/s，待流速稳定后，施加白噪声激励，当信号稳定后，同时获取所有声测点位置处的时域、频域信息。流速云图分别如图3所示。

各流速工况下试验结果如表1所示，可以发现，随着流速的增加，各阶模态的频率值逐渐减小，该试验结果与理论推导结果一致。

表1 不同流速模态频率试验结果对比

4 考虑平均流速效应数值计算

在试验结果基础上开展了基于理论推导的数值计算，基于标准一维模型研究了平均流速对声腔模态频率特性的影响，根据理论推导分别考虑了平均流速附加刚度及附加阻尼的影响，研究了平均流速对声学系统控制方程中刚度矩阵及阻尼矩阵的影响及作用效果，从而揭示了平均流速存在对燃烧室声学系统频率影响的物理机理。

4.1 平均流速附加刚度对声模态影响分析

为了验证理论推导的正确性，首先开展了一维圆柱燃烧室模型常温常压下仅考虑平均流速刚度改变对系统模态特性的影响，模型长=1000mm。分别计算了不同速度下流速与燃烧室模态频率的关系，计算结果如图4所示。

图4 标准一维圆柱不同阶频率与平均流速关系（不考虑流速阻尼）

根据式(24)，随着平均流速的提高，系统刚度逐渐降低，当流速达到当地声速时，系统刚度降低至零。计算结果表明，考虑平均流速情况时，随着平均流速的提高，相同状态下燃烧室模态频率逐渐降低。静止状态下（平均流速为零）本文计算结果与如下标准一维声腔频率公式结果一致

式中，为声速、为长度、为模态阶数。

根据理论结果，首先开展了静止状态燃烧室声模态特性，在静止状态模型基础上，通过施加速度场方式计算研究了不同流速对燃烧室模态频率特性的影响规律。分别计算平均流速为100m/s、300m/s两个状态下燃烧室模态频率，不同流速下本文与有限元计算结果对比如表2所示。

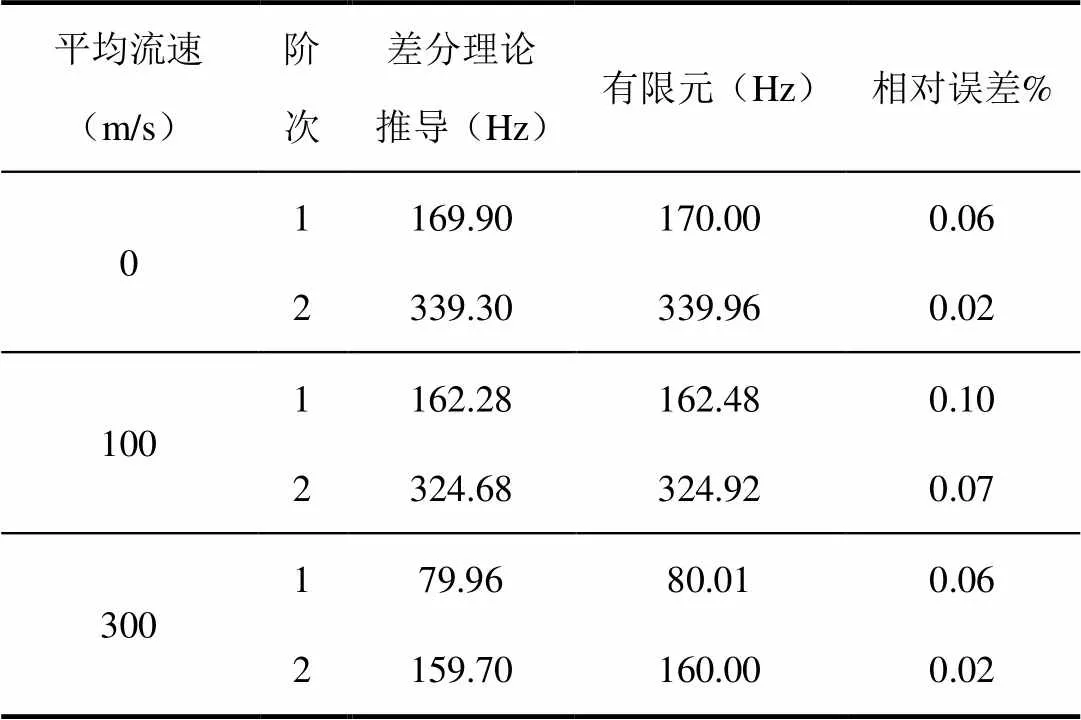
表2 不同流速燃烧室模态频率理论仿真结果对比

以上结果表明，本文方法与试验结果定性一致，与标准有限元模型结果基本一致，证明本文理论推导及数值计算的合理。考虑平均流速情况时，随着平均流速的提高，相同状态下燃烧室模态频率逐渐降低，当平均流速达到当地声速时，燃烧室声学系统刚度将变为零，从而造成系统各阶模态频率均趋向零。

4.2 平均流速附加阻尼对声模态影响分析

根据式(19)，平均流速的存在不仅改变了燃烧室声学系统的刚度，而且改变了燃烧室声学系统的阻尼。由于平均流速的存在，系统将产生一个与平均流速相关的阻尼项，且该阻尼项与流速呈正比，随着流速的提高，附加阻尼将线性增加。因此，工程中必须综合考虑平均流速所产生附加阻尼及刚度效应对燃烧室声学特性的共同影响。

考虑附加阻尼项后，不同阶燃烧室频率与流速之间的对应关系理论推导计算结果如图5所示。根据计算结果可知，平均流速所导致的附加阻尼项将进一步改变系统的频率特性，随着流速的提高，附加阻尼线性增加。在附加刚度及阻尼作用下，系统的频率变化与流速存在非线性关系。随着流速的提高，系统频率非线性快速降低，但考虑附加阻尼项后不同阶模态频率之间仍存在倍频关系。有无附加阻尼情况下系统频率与流速关系如图6所示。结果表明，考虑阻尼项后相同流速下系统模态频率将进一步降低。

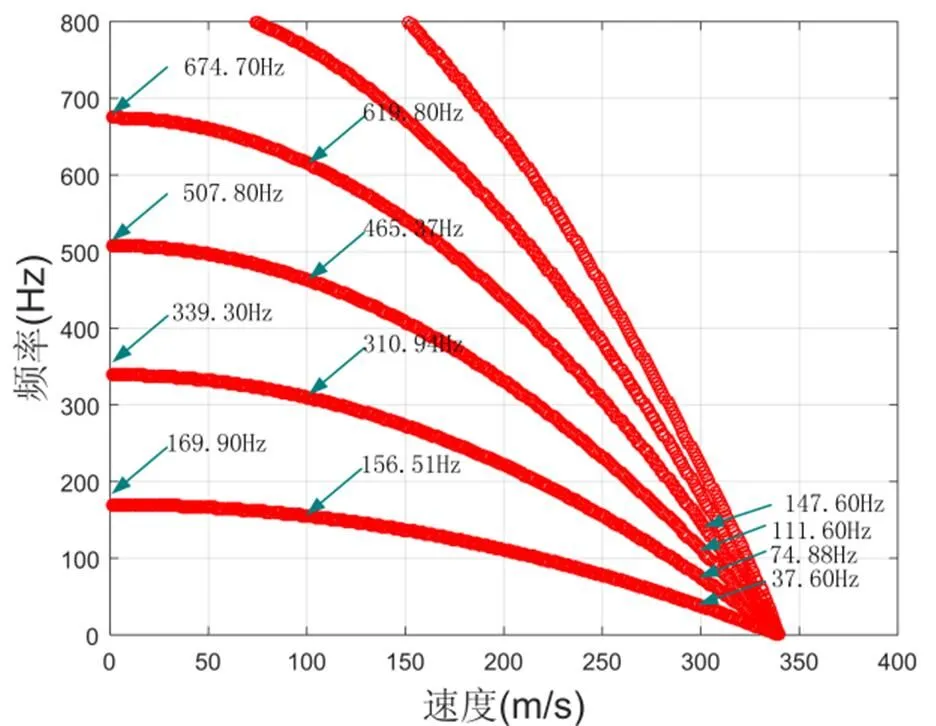
图5 标准一维圆柱不同阶模态频率与平均流速关系（考虑流速阻尼）

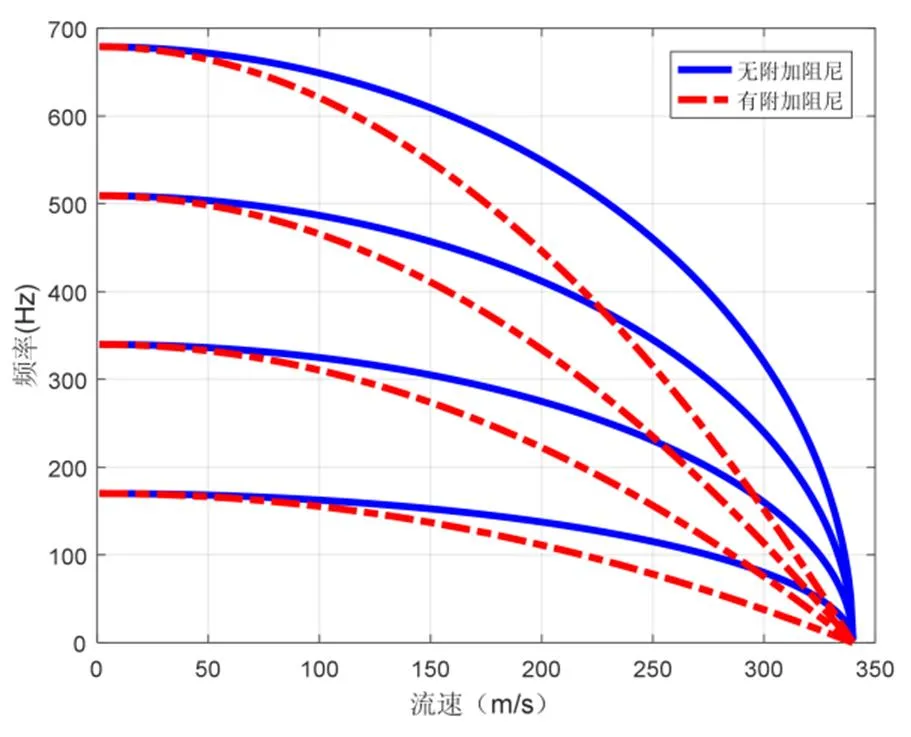
图6 有无附加阻尼系统频率与流速关系

为验证开展了有限元仿真分析，计算获得了不同流速下系统的频响特性，结果如图7所示。本文方法与有限元计算结果基本一致。随着流速的提高，在附加刚度及阻尼项作用下，系统基频将迅速降低。

根据以上计算结果可知，在考虑平均流速所产生阻尼特性情况下，平均流速的存在进一步改变了燃烧室模态的频率值，相对仅考虑刚度改变项，流速阻尼将进一步降低系统的频率，然而，相同流速下不同阶模态频率间仍存在严格的倍频关系。随着平均流速的提高，燃烧室模态频率降低，当平均流速达到当地声速时，所有阶燃烧室模态频率同样都将趋近于零。表3综合对比了理论计算与有限元计算结果对比，给出了不同流速下综合考虑附加阻尼及刚度效应后系统相对静止状态频率变化率，随着平均流速的提高，系统频率变化率明显提高，平均流速在100m/s以内时，频率变化率在10%以内，但当平均流速达到300m/s时，频率变化率达到了77.9%。

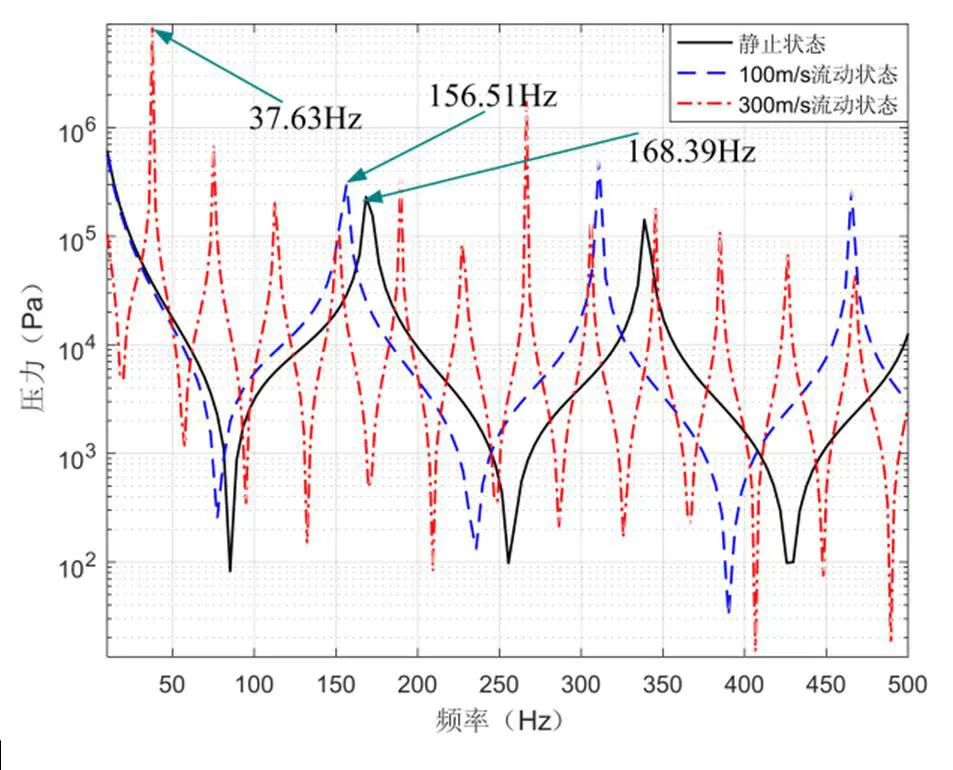
图7 不同流速下频响特性曲线

表3 不同流速燃烧室模态频率理论仿真结果对比

5 结论

发动机燃烧室声模态频率受到燃烧室内平均流速对刚度及阻尼的影响：1)平均流速的存在不仅改变了系统的刚度特性，而且改变了系统的阻尼特性。随着流速的提高，系统刚度逐渐降低，系统阻尼与流速呈正比，系统各阶模态频率逐渐降低，当流速达到当地声速时，系统各阶模态频率均将趋近于零；2)平均流速的存在虽然改变了系统各阶模态频率值，但标准一维模型各阶模态频率值之间仍然存在倍频关系；3)考虑内流速场对固体火箭发动机声腔模态特性的影响，为精确消除真实固体火箭发动机工作过程中声固耦合可能触发的燃烧不稳定问题提供了解决技术途径。由于真实发动机工作过程中内部流速及温度为非均匀分布的复杂物理场，而且，真实发动机内部声腔构型沿轴向存在截面变化特性。因此，后续结合试验结果将开展考虑非均匀物理场情况下实际发动机声腔模态特性。

[1] 张翔宇, 高波, 甘晓松,等. 飞行过载对固体火箭发动机不稳定燃烧的影响[J]. 宇航学报, 2019, 40(8): 972-976.[Zhang Xiangyu, Gao Bo, Gan Xiaosong, et al. Impacts of flight acceleration on combustion instability of solid rocket motor [J]. Journal of Astronautics, 2019, 40(8): 972-976.]

[2] 苏万兴, 李世鹏, 张峤, 等. 某固体火箭发动机工作末期不稳定燃烧数值研究[J]. 航空动力学报, 2013, 28(10): 2376-2383. [Su Wanxing, Li Shipeng, Zhang Qiao, et al. Combustion instability at end of burning in a solid rocket motor[J]. Journal of Aerospace Power, 2013, 28(10): 2376-2383.]

[3] 陈晓龙, 何国强, 刘佩进, 等. 潜入式喷管对燃烧室中压力振荡的影响[J]. 固体火箭技术, 2010, 33(3): 252-255. [Chen Xiaolong, He Guoqiang, Liu Peijin, et al. Effect of submerged nozzle on pressure oscillation in chamber [J]. Journal of Solid Rocket Technology, 2010, 33(3): 252-255.]

[4] 刘佩进, 齐宗满, 金秉宁, 等. 两种含铝复合推进剂压强耦合响应的实验对比[J]. 固体火箭技术, 2013, 36(1): 83-88.[Liu Peijin, Qi Zongman, Jin Bingning, et al. Experiment comparison of pressure coupled response of the aluminized composite propellants [J]. Journal of Solid Rocket Technology, 2013, 36(1): 83-88.]

[5] 吴毅, 胡博文, 孟惠. 某型固体火箭发动机低温燃烧不稳定现象分析[J]. 弹箭与制导学报, 2016, 36(4): 67-69. [Wu Yi, Hu Bowen, Meng Hui. Analysis of combustion instability in low-temperature ground test of a solid rocket motor [J]. Journal of Projectiles, Rockets, Missiles and Guidance, 2016, 36(4): 67-69.]

[6] 杨尚荣, 刘佩进, 魏祥庚, 等. 固体火箭发动机径向加质流局部稳定性分析方法研究[J]. 推进技术, 2013, 34(7): 925-931. [Yang Shangrong, Liu Peijin, Wei Xianggeng, et al. A Study of analysis method for hydrodynamic stabilities of solid rocket motors with side-induced flow[J]. Journal of Propulsion Technology, 2013, 34(7): 925-931.]

[7] 杨尚荣, 刘佩进, 魏少娟, 等. 考虑径向加质的固体火箭发动机内流场整体稳定性分析[J]. 固体火箭技术, 2013, 36(6): 727-730. [Yang Shangrong, Liu Peijin, Wei Shaojuan, et al. Biglobal stability analysis for the side-induced flow in solid rocket motors[J]. Journal of Solid Rocket Technology, 2013, 36(6): 727-730.]

[8] 王宁飞, 张峤, 李军伟, 等. 固体火箭发动机不稳定燃烧研究进展[J]. 航空动力学报, 2011, 26(6): 1405-1414.[Wang Ningfei, Zhang Qiao, Li Junwei, et al. Progress of investigation on combustion instability of solid rocket motors[J]. Journal of Aerospace Power, 2011, 26(6): 1405-1414.]

[9] 苏万兴, 李世鹏, 张峤, 等. 某固体火箭发动机工作末期不稳定燃烧航空动力学报[J]. 2013, 28(10): 2376-2383.[Su Wanxing, Li Shipeng, Zhang Qiao, et al. Combustion instability at end of burning in a solid rocket motor[J]. Journal of Aerospace Power, 2013, 28(10): 2376-2383.]

[10] 陈书明, 王登峰, 宋学伟, 等. 基于FE-SEA混合方法的燃烧室内部噪声预测[J]. 振动与冲击, 2010, 29(10): 236-238. [Chen Shuming, Wang Dengfeng, Song Xuewei, et al. In-car noise prediction based on hybrid FE-SEA model[J]. Journal of Vibration and Shock, 2010, 29(10): 236-238.]

[11] 侯亮, 杨维平, 蔡惠坤, 等. 基于燃烧室与结构模态分析的动力舱共振规避[J]. 中国工程机械学报, 2015, 13(5): 394-399. [Hou Liang, Yang Weiping, Cai Huikun, et al. Resonance avoidance of engine compartment based on acoustic and structural modal analysis[J]. Chinese Journal of Construction Machinery, 2015, 13(5): 394-399.]

[12] 赵艳栋. 双脉冲固体火箭发动机燃烧室压强振荡特性分析[D]. 北京: 北京理工大学, 2016.

[13] 杨向明, 刘佩进, 陈晓龙. 翼柱型装药固体火箭发动机燃烧室声场分析[J]. 宇航学报, 2008, 29(5): 1593-1597. [Yang Xiangming, Liu Peijin, Chen Xiaolong. Analyze of acoustic property with complicated grain shape in combustion chamber of solid rocket motor[J]. Journal of Astronautics, 2008, 29(5): 1593-1597.]

[14] 胡大宁, 何国强, 刘佩进, 等. 翼柱型药柱固体火箭发动机不稳定燃烧研究[J]. 固体火箭技术, 2010, 33(5): 502-506.[Hu Daning, He Guoqiang, Liu Peijin, et al. Study on combustion instability of solid rocket motor with finocyl grain [J]. Journal of Solid Rocket Technology, 2010, 33(5): 502-506.]

[15] 秦朝红, 任方, 王英诚, 等. 复杂结构全频段声振综合响应分析[J]. 强度与环境, 2017, 44(6): 8-14. [Qin Zhaohong, Ren Fang Wang Yingcheng et al. Vibro-acoustic analysis of complex structure in whole frequency band[J]. Structure & Environment Engineering, 2017, 44(6): 8-14.]

[16] Vijaya Krishna Rani, Sarma L Rani. WKB solutions to the quasi 1-D acoustic wave equation in ducts with non-uniform cross-section and inhomogeneous mean flow properties Acoustic field and combustion instability [J]. Journal of Sound and Vibration, 2018, 43(6): 183-219.

[17] Alexander G. Wilson. Calculation of Acoustic Transfer Functions for Smooth Ducts of Varying Cross Section and Non-Uniform Mean Flow using Eigen Analysis in General Curvilinear Coordinates [C]. AIAA/CEAS Aeroacoustics Conference, 2018:1-16.

[18] Jingxuan Li, Dongbin Wang, AS Morgans, Lijun Yang. Analytical solutions of acoustic field in annular combustion chambers with non-uniform cross-sectional surface area and mean flow [J]. Journal of Sound and Vibration, 2021, 50(6): 116-175.

[19] SR Yeddula, AS Morgans. A semi-analytical solution for acoustic wave propagation in varying area ducts with mean flow [J]. Journal of Sound and Vibration, 2021, 49(2): 11577.

The Study of Axial Mean Flow Velocity of Solid Rocket Motor Combustion Chamber on Acoustic Mode

LIU Lu-guang1HOU Kai-yu2SHI Xiao-ming1XIA Peng1LI Hai-dong1GAO Yang1LI Hai-bo3

(1 Shanghai Electro-mechanical Engineering Institute, Shanghai 201109,China; 2 Shanghai Academy of Spaceflight Technology, Shanghai 201109,China;3 Beijing Institute of Structure and Environment Engineering, Beijing 100076, China）

The unstable combustion of solid rocket motor is closely related to the acoustic modal characteristics of the combustion chamber，reducing the coupling between the combustion chamber and the vortex shedding frequency can greatly reduce the occurrence of unstable combustion. However, the present research are mainly based on the static state of the medium in the combustion chamber, the mean flow characteristic of the gas medium in the combustion chamber are not considered. This paper is based on the unstable combustion of solid rocket motor with large aspect ratio, through theoretical derivation and numerical simulation to research the mechanism and characteristics of axial mean flow velocity on chamber frequency. The results show that the existence of mean flow not only changes the stiffness characteristics of the combustion chamber, moreover, a damping term proportional to the mean flow velocity is also generated, thereby the acoustic modal characteristics of the combustion chamber is changed.

Solid rocket motor; Unstable combustion; Additional stiffness; Additional damping; Mean flow velocity

V435

A

1006-3919(2022)03-0020-08

10.19447/j.cnki.11-1773/v.2022.03.004

2022-02-14；

2022-05-09

刘陆广（1983—），男，博士，高级工程师，研究方向：飞行器总体设计；（201109）上海市闵行区元江路3888号.