新型零泊松比类蜂窝结构面内变形性能研究

廖学知 王洪波 李宝玉 赵晓宁

新型零泊松比类蜂窝结构面内变形性能研究

廖学知1王洪波2李宝玉1赵晓宁1

(1 中国运载火箭技术研究院, 北京 100076; 2 中国航天科技集团有限公司, 北京 100048）

飞行器实现智能变形的物质基础是结构具有出色的面内变形性能。本文基于零泊松比蜂窝结构的面内力学特性，结合波纹结构出色的变形能力，提出了以波纹结构替代蜂窝壁的新型零泊松比类蜂窝结构形式，并结合理论建模与仿真分析的方法对其面内变形性能进行分析。结果表明该结构面内变形性能相对于六边形蜂窝结构具有有效提升；采用较小的蜂窝角、壁厚比以及较大的波纹度有利于获得具有更小等效刚度和更大应变放大系数的结构。该结果可为一维伸缩变形结构的设计与优化提供相应参考。

零泊松比；蜂窝结构；波纹结构；力学性能；

0 引言

变形飞行器可针对不同的飞行任务和飞行环境，自适应改变自身气动外形，获得更优的飞行性能，因而成为飞行器发展的主要研究方向之一[1-3]。其中可变形结构一直是变形飞行器中材料与结构核心研究对象，为了适应结构的大变形，结构需要具有较低的面内刚度及较大的变形能力，以减小变形过程中对驱动力的要求并满足位移变化需求[4]。

蜂窝结构作为可变形结构的典型代表，依赖于自身的拓扑形式可呈现出不同的力学特性和泊松比效应，以满足各种变形需求，由于其具有轻质量以及可设计性强的优点，吸引了国内外众多工程技术人员研究。Gibson等[5]基于欧拉梁弯曲理论推导了六边形蜂窝面内弹性模量、泊松比和剪切模量，并研究了六边形蜂窝的屈曲和塑性力学性能。王颖坚[6]修正了Gibson理论模型，建立了更加准确的面内剪切模量理论公式。Evans等[7]建立了考虑六边形蜂窝壁弯曲变形、拉压变形和蜂窝壁夹角变化的面内弹性常数一般模型理论。富明慧[8]通过考虑六边形蜂窝壁拉压变形而对Gibson理论进行修改。在变形飞行过程中，采用零泊松比结构可实现以变展长为例的一维变形过程，且不影响弦长的变化，因此可简化变形翼的结构设计和控制系统的复杂度。刘卫东[9, 10]对零泊松比手风琴蜂窝结构的面内外等效模量进行了理论建模与参数分析。Chen[11]基于剪纸工艺研制了弯曲型零泊松比SILICOMB蜂窝样件，并对其刚度性能进行了研究。Gong[12]提出了一种四角星形零泊松比蜂窝结构，可实现两个正交方向的变形，且能在变形时保证整体结构曲率光滑。黄建[13]提出了一种将传统六边形蜂窝结构与薄板连接组装在一起的新型零泊松比构型，并建立了结构的等效弯曲模量的理论表达式。艾森[14]等以铝合金和钢材为基体材料，针对零泊松比蜂窝结构的非线性变形行为进行了研究。与蜂窝结构类似，波纹结构也具有各向异性的特点，其力学行为的等效模型已被广泛研究。Gong[15]将正弦型剖面波纹板的横向拉伸、弯曲刚度进行了理论建模。Winkler[16]等研究了不同波纹形状对波纹结构的等效刚度的影响。Bartolozzi[17]提出了用于表征波纹结构性能的一般解析公式，可适用于不同的波纹形状。本文为提高结构的面内变形性能，提出一种新型零泊松比类蜂窝结构，该结构使用波纹结构替代蜂窝斜壁，当波纹度为0时即可退化为六边形蜂窝结构。综合考虑结构的弯曲、拉伸变形，对新型零泊松比类蜂窝结构的面内等效弹性模量、等效刚度和应变放大系数进行了理论推导与有限元仿真，并与六边形蜂窝结构的现有理论解进行了性能对比；分析了结构参数对其变形性能的影响。获得的相关结论可为伸缩变形结构的优化设计、材料选型等提供重要支撑。

1 新型结构力学建模与仿真

1.1 新型零泊松比类蜂窝结构胞元

新型零泊松比类蜂窝结构胞元的几何构型如图1所示，其结构是在六边形蜂窝结构基础上，将倾斜胞壁转换为波纹结构，以获得更出色的面内变形性能；此外采用横梁连接各个独立胞元，使得该结构在纵向伸缩时，横向变形可忽略，因此呈现出典型的零泊松比特性，有利于一维伸缩变形。取其单胞结构进行分析，采用与蜂窝结构类似的参数定义方法，胞元倾斜壁直线长度为，直壁长度为，蜂窝角为，壁厚为；对于胞元斜壁定义波纹幅值为，此外定义壁高度为。

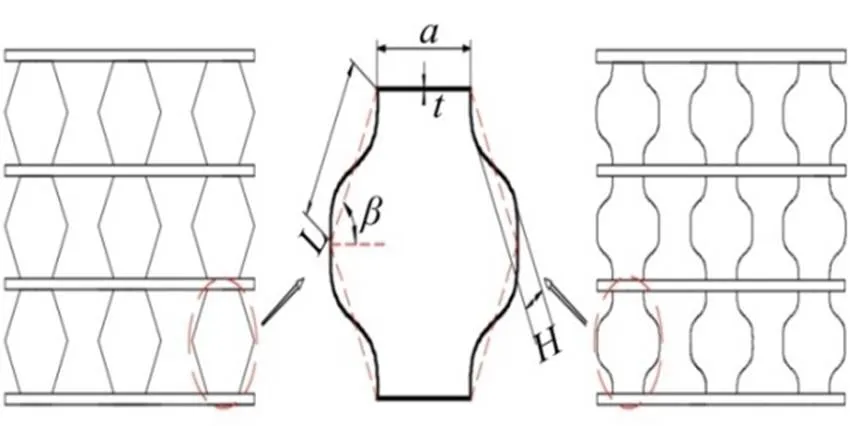
图1 新型零泊松比结构示意图

1.2 理论模型

面内变形能力主要取决于单胞元结构，而横梁主要用于构造零泊松比特性，因此可选取如图2所示最小特征单元进行分析。假设结构受纵向单向拉伸时，结构的变形主要由斜壁板的弹性变形引起。此外，由于结构的对称性，可选取波纹斜壁板OA作为最小特征研究对象。

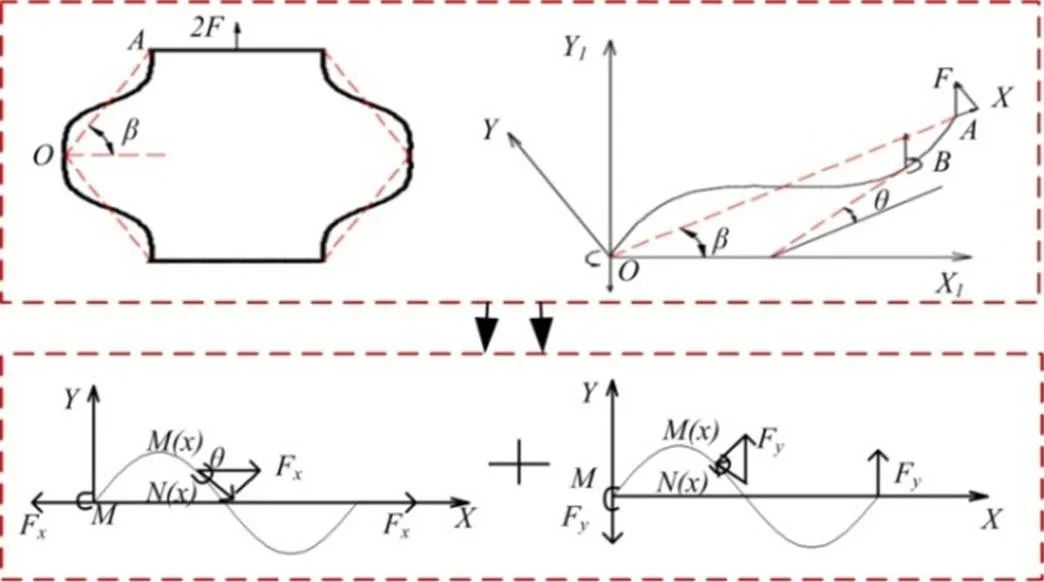
图2 结构纵向拉伸示意图

为方便对波纹斜壁板进行变形分析，沿斜壁方向建立如图2所示坐标系，在该坐标系下波纹斜壁板满足以下几何关系

对纵向外力进行分解，获得沿波纹壁延伸方向和垂直方向的力为

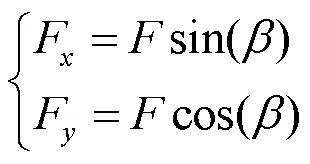
接下来分别对两种受力情况进行分析：首先对沿波纹壁延伸方向力引起的变形进行分析，选取任意截面，根据力平衡和力矩平衡可以得到截面上的受力如下

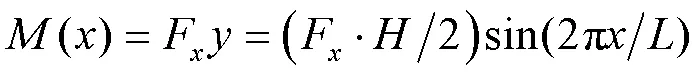
忽略剪切变形，仅考虑轴向和弯曲变形。由卡式第二定理得变形位移为

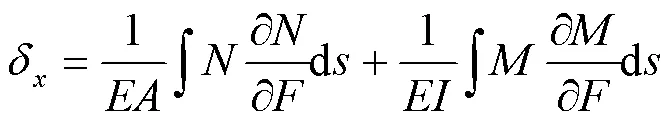
其中为材料弹性模量，和分别为截面面积和截面惯性矩。

根据结构的几何关系式（1）可得

联立等式（3）～（6），进一步可得

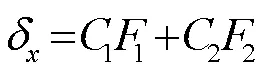
其中

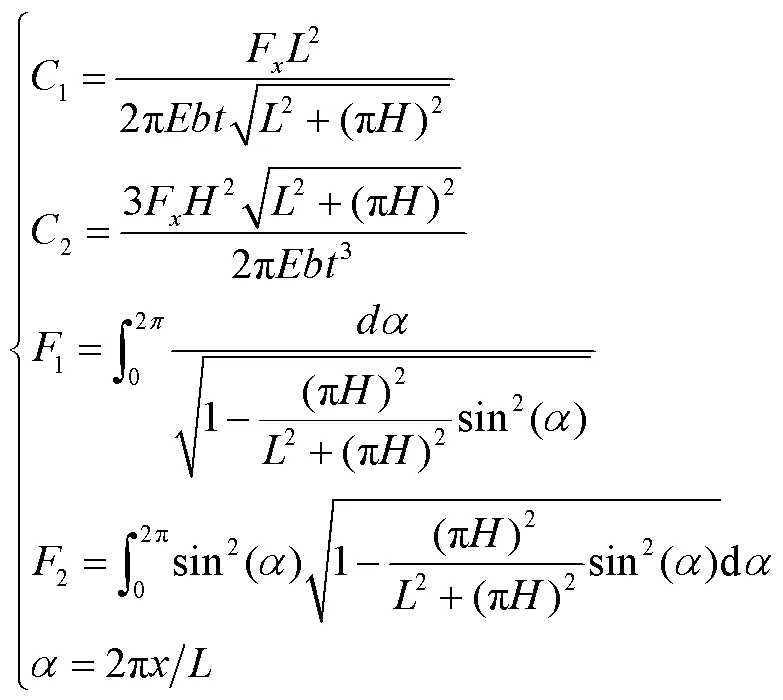
同理对垂直力引起的变形进行分析，选取任意截面，可得截面受力为

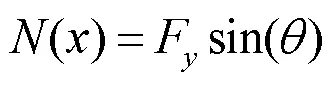
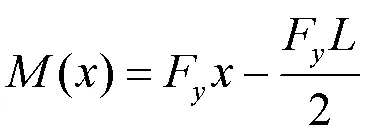
同样由卡式第二定理得变形位移如下

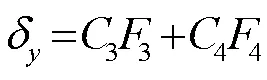
其中

根据坐标变换关系，可得纵向总位移如下

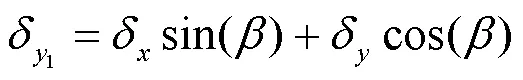
对于该新型结构，其面内等效弹性应力和应变如下

进一步可得无量纲等效弹性模量如下

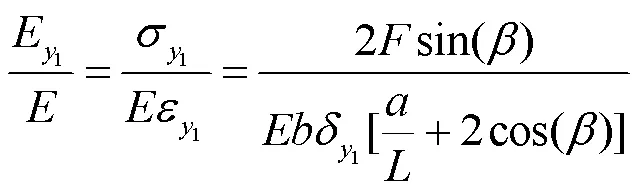
此外为衡量所需驱动力的大小，对等效刚度进行推导，得

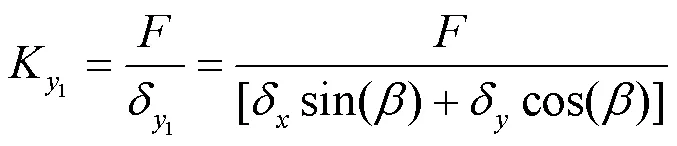
新型结构的面内变形主要是由于波纹斜壁的母体材料弹性应变随几何形状的累积而放大，而当蜂窝结构中的局部应变超过材料屈服极限时，则会发生塑性变形，影响结构的使用。因此除等效刚度之外，定义蜂窝等效应变和材料最大正应变之比为应变放大系数，以此来表征变形能力[18]。

对于单向拉伸时蜂窝材料，材料应变为

最大应变在弯矩最大处，可近似为波纹斜壁端点处

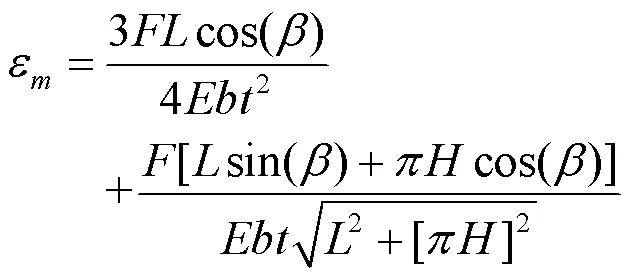
因此可得变形放大因子

1.3 单胞的数值模拟计算

有限元数值分析常用来对理论分析模型进行验证。本文采用Abaqus软件对结构的纵向拉伸刚度，以及应变放大系数的理论预测模型进行验证。有限元数值分析选取一个单胞元，考虑到壁厚相对较小，应用S4R壳单元进行模拟，分析模型如所示。本研究中尚不考虑材料的非线性，并采用各向同性材料进行数值模拟，材料弹性模量设置为200GPa和材料泊松比为0.3。边界约束及加载方式如图3所示，采用边界上的约束反力与位移的比值表征纵向拉伸刚度，采用等效应变值与材料最大应变值表征应变放大系数。

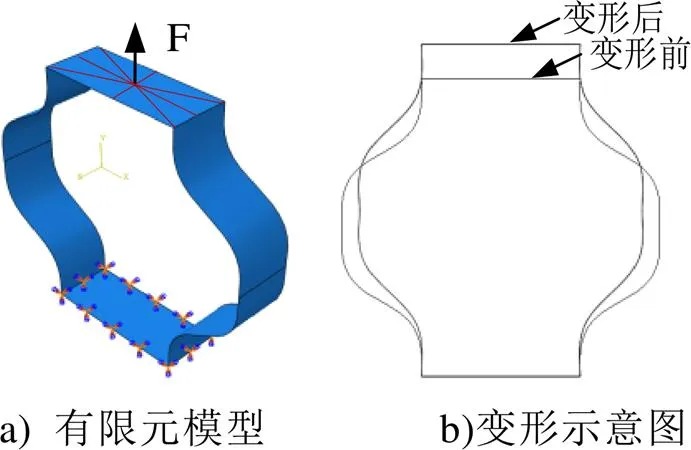
图3 有限元模型示意图

2 结果分析与讨论

2.1 理论解与有限元结果的对比

当波纹度/为0时，则可退化为六边形蜂窝结构。选取与文献[19]相同的几何参数，取厚度比为0.1，斜壁长、直壁长及壁高分别为10mm、10mm和4mm。本文无量纲等效弹性模量理论解与现有理论解及有限元结果的对比情况如图4所示。从图4中可以看出，三者结果高度吻合，验证了本文理论模型及有限元模型的正确性。

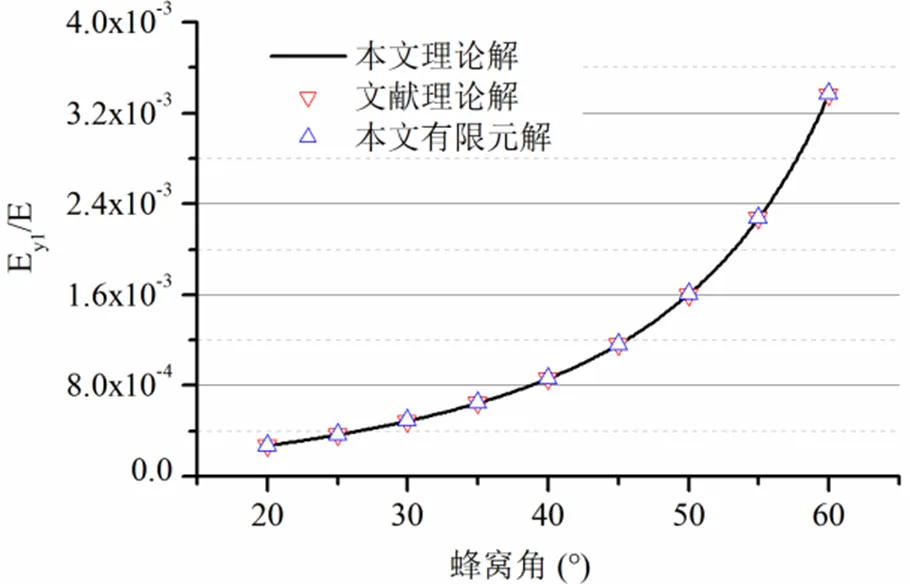
图4 无量纲等效弹性模量随蜂窝角的变化

2.2 波纹度对面内变形性能的影响

本文提出的新型零泊松比类蜂窝结构在波纹度/为0时，与传统六边形蜂窝结构一致。为验证本文新结构相比于六边形蜂窝结构性能的变化，对比了不同波纹度情况下，面内变形性能的变化规律。

以厚度比为0.02、0.04、0.08，高度比为0.4，蜂窝角为20°时的数据为例进行分析，结果如图5所示。可以发现在不同厚度比条件下，等效刚度均随波纹度的增大而降低，且随厚度比的增大而大幅增大；应变放大系数随着波纹度的增大而增大，随厚度比的增大而大幅降低。这是由于波纹度的增大，导致波纹壁更易产生弯曲变形，进而变形能力进一步提高。等效刚度降低，有利于结构的纵向伸缩变形能力，降低变形所需的驱动力；放大系数显著增大，有利于结构在失效前获得更大的变形范围。综合这两方面的指标可以发现波纹斜壁的引入使得新型结构面内变形能力得到显著增强。

此外，从图5中可以看出，理论等效刚度略高于有限元结果，应变放大系数低于有限元结果，这是由于理论推导过程未考虑剪切变形的影响。但平均误差均在8%左右，说明本文理论解与有限元仿真结果吻合程度较好，验证了理论公式在不同厚度比、波纹度条件下的有效性，以及有限元模型简化的合理性。

图5 变形性能随波纹度的变化（β=20°, a/L=1, b/L=0.4）

2.3 几何参数对面内变形性能的影响

利用所获得的理论模型研究结构几何参数对等效刚度及应变放大系数等面内变形性能指标的影响规律。通过上述理论推导，可以发现等效刚度及放大系数与直壁长度无关，因此不对其进行参数分析，在下述分析中均取直壁长度比为1。首先对不同波纹度下，等效刚度和放大系数随蜂窝角的变化规律进行研究。选取厚度比为0.01，高度比为0.4时的数据进行分析，其他厚度和高度下的变化趋势与此类似，值得注意的是当波纹度为0时该结构则退化为六边形蜂窝结构。结果如图6所示，可以发现等效刚度随蜂窝角的增大而增大，且变化速度也逐渐变大，这是由于蜂窝角的增大使得拉伸导致的变形逐渐凸显，而弯曲变形逐渐削弱所致。对于放大系数，其呈现出随着蜂窝角的增大而减小的变化趋势，并逐渐趋于平稳。综合两者的变化规律，可以发现在小蜂窝角、大波纹度条件下，结构变形以斜壁的弯曲变形为主，这有利于结构的面内变形。

图6 变形性能随蜂窝角的变化（t/L=0.1, b/L=0.4, a/L=1）

结构面内变形性能随厚度比的变化如图7所示，其中蜂窝角为20°，高度比为0.4。可以发现等效刚度随厚度比的增大而增大，放大系数随着厚度比的增大而减小，且波纹斜壁的引入显著提升了其面内变形性能。综合两者的变化规律，可以发现在小壁厚、大波纹度条件下，有利于结构的面内变形性能的提升。

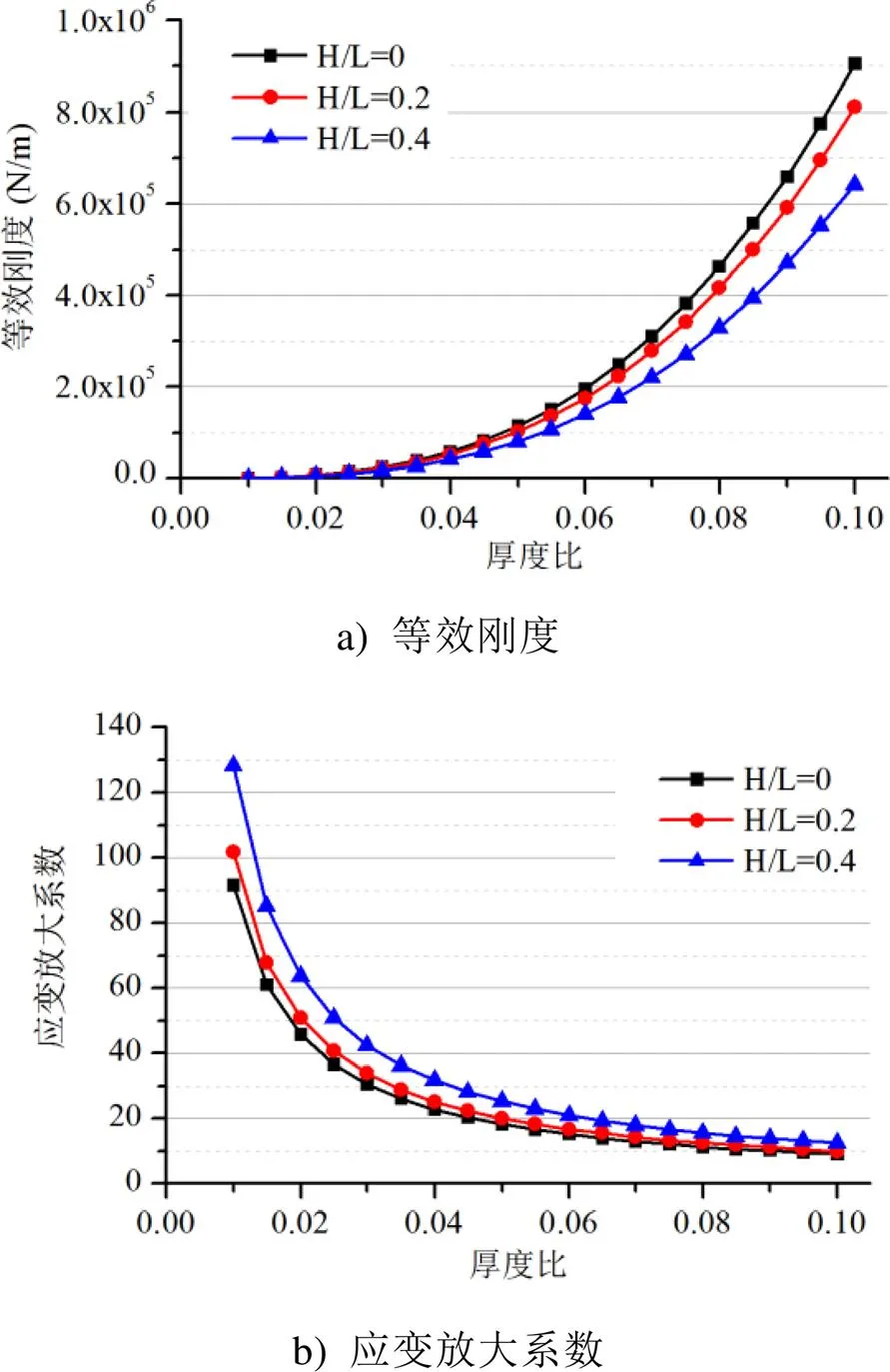
图7 变形性能随厚度比的变化（β=20°, b/L=0.4, a/L=1）

结构面内变形性能随高度比的变化如图8所示，其中蜂窝角为20°，厚度比为0.1。从图中可以发现等效刚度随高度比的增大呈现出线性增大的变化规律，而放大系数则与高度比无关。此外通过与波纹度为0时的结构进行对比，可以发现波纹斜壁使得等效刚度明显降低，而应变放大系数得到了有效提升。

图8 变形性能随高度比的变化（β=20°, t/L=0.1, a/L=1）

3 结论

本文对新型结构的面内变形性能进行理论计算，结合有限元仿真进行比较验证。通过与六边形蜂窝结构面内变形能力进行对比研究，以及结构参数化分析，得出以下结论：

1）在相同参数条件下相比于六边形蜂窝结构，波纹斜壁的引入使得新结构的等效刚度降低，应变放大系数增大，因此具有更为出色的面内变形能力；

2）纵向等效刚度随波纹度的增大而减小，随厚度比、蜂窝角的增大而增大，且与高度比呈线性正相关；

3）放大因子随波纹度的增大而增大，随厚度比、蜂窝角度的增大而减小，且与高度比无关。

后续将进一步考虑面板的影响，并对其他方向的力学性能进行深入研究，促进其工程实践的应用。

[1] 马征. 国外下一代战斗机和高超声速飞机结构技术发展综述[J]. 强度与环境, 2021, 48(5): 15-21.[Ma Zheng. Overview of the structural technology development of foreign next-generation fighters and hypersonic aircraft[J]. Structure & Environment Engineering, 2021, 48(5): 15-21.]

[2] 冷劲松, 孙健, 刘彦菊. 智能材料和结构在变体飞行器上的应用现状与前景展望[J]. 航空学报, 2014, 35(1): 29-45.[Leng Jingsong, Sun J, Liu Y J. Application status and future prospect of smart material and structures in morphing aircraft[J]. Acta Aeronautica et Astronautica Sinica, 2014, 35(1): 29-45.]

[3] 白鹏, 陈钱, 徐国武, 等. 智能可变形飞行器关键技术发展现状及展望[J]. 空气动力学学报. 2019, 37(3): 426-443.[Bai Peng, Chen Qian, Xu Guowu, et al. Development status of key technologies and expectation about smart morphing aircraft[J]. Acta Aerodynamica Sinica, 2019, 37(3):426-443.]

[4] 尹维龙, 石庆华. 变体飞行器蒙皮材料与结构研究综述[J]. 航空制造技术, 2017(17): 24-29.[Yin Weilong, Shi Qinghua. Review of material and structure for morphing aircraft skin[J]. Aeronautical manufacturing technology, 2017 (17): 24-29.]

[5] Gibson L J, Ashby M, Schajer G, et al. The mechanics of two-dimensional cellular materials[J]. Proceedings of the Royal Society of London, 1982, 382(1782): 43-59.

[6] 王颖坚. 蜂窝结构在面内剪力作用下的变形模式[J]. 北京大学学报(自然科学版), 1991(3): 301-307.[Wang Yinjian. Deformation models of honeycomb cell under in-plane shear[J]. Acta Scicentiarum Naturalum Universitis Pekinesis, 1991(3): 301-307.]

[7] Masters I G, Evans K E. Models for the elastic deformation of honeycombs[J]. Composite Structures, 1996, 35(4): 403-422.

[8] 富明慧, 尹久仁. 蜂窝芯层的等效弹性参数[J]. 力学学报, 1999, 31(1): 113-118.[Fu Minghui, Yin Jiuren. Equivalent elastic parameters of the honeycomb core[J]. Acta Mechanica Sinica, 1999, 31(1):113-118.]

[9] 刘卫东, 李红林. 零泊松比手风琴蜂窝等效模量[J]. 固体力学学报, 2018, 39(1): 100-112. [Liu Weidong, Li Honglin. Equivalent modulus of accordion honeycomb with zero Poisson’s ratio[J]. Acta Mechanica Solida Sinica, 2018, 39(1): 100-112.]

[10] Liu W D, Zhu H, Zhou S Q, et al. In-plane corrugated cosine honeycomb for 1D morphing skin and its application on variable camber wing[J]. Chinese Journal of Aeronautics, 2013, 26(4): 935-942.

[11] Chen Y, Scarpa F, Remillat C, et al. Curved Kirigami SILICOMB cellular structures with zero Poisson's ratio for large deformations and morphing[J]. Journal of Intelligent Material Systems and Structures, 2013, 25(6): 731-743.

[12] Gong X B, Huang J, Scarpa F, et al. Zero Poisson's ratio cellular structure for two-dimensional morphing applications [J]. Composite Structures, 2015, 134(15): 384-392.

[13] 黄建. 新型零泊松比蜂窝结构力学性能及其变弯度机翼应用研究[D]. 哈尔滨工业大学, 2018. [Huang Jian. Mechanical performances of a novel honeycomb design with zero poisson's ratio and its application in camber morphing wings[D]. Harbin: Harbin Institute of Technology, 2018.]

[14] 艾森, 郭瑜超, 聂小华, 等. 零泊松比蜂窝结构一维变形行为[J]. 南京航空航天大学学报, 2021, 53(4): 629-636.[Ai Sen, Guo Yuchao, Nie Xiaohua, et al. One-dimensional deformation behavior of a honeycomb structure with zero poisson's ratio[J]. Journal of Nanjing University of Aeronautics & Astronautics, 2021, 53(4): 629-636.]

[15] Gong X B, Liu L W, Scarpa F, et al. Variable stiffness corrugated composite structure with shape memory polymer for morphing skin applications [J]. Smart Materials and Structures, 2017, 26(3), 035052.

[16] Winkler M, Kress G. Influence of corrugation geometry on the substitute stiffness matrix of corrugated laminates [J]. Composite Structures, 2012, 94: 2827-2833.

[17] Bartolozzi G, Baldanzini N, Pierini M. Equivalent properties for corrugated cores of sandwich structures: A general analytical method [J].Composite Structures, 2014, 108: 734-746.

[18] 阚文广, 尹维龙. 可变形蜂窝结构设计与力学分析[J]. 哈尔滨工程大学学报, 2017, 38(9):1406-1412.[Kan Wenguang, Yin Weilong. Design and mechanical analysis of deformable honeycomb structures [J]. Journal of Harbin Engineering University, 2017, 38(9): 1406-1412.]

[19] Huang J, Gong X B, Zhang Q, et al. In-plane mechanics of a novel zero poisson's ratio honeycomb core[J]. Composite Part B Engineering, 2015, 89(15): 67-76.

Study on In-Plane Deformation Performance of a Novel Zero Poisson’s Ratio Quasi-Honeycomb Structure

LIAO Xue-zhi1WANG Hong-bo2LI Bao-yu1ZHAO Xiao-ning1

(1 China Academy of Launch Vehicle Technology, Beijing 100076, China;2 China Aerospace Science and Technology Corporation, Beijing 100048, China)

The structure with excellent in-plane deformation performance is the material base for smart morphing aircraft. Based on the zero Poisson’s ratio honeycomb structure and the corrugated structure, a new zero Poisson’s ratio structure is proposed in this paper, and its in-plane deformation performance is analyzed by theoretical and finite element modeling. The results show that the in-plane deformation performance of the structure is improved effectively compared with the traditional honeycomb structure. Smaller cell angle, wall thickness ratio and larger corrugation ratios are beneficial to obtain structures with smaller equivalent stiffness and larger strain amplification coefficient. The results provide a useful theoretical basis and technical support for the design and optimization of morphing structure.

Zero Poisson’s ratio; Honeycomb structure; Corrugated structure; Mechanical characteristic

TB332,V417+.4

A

1006-3919(2022)03-0001-07

10.19447/j.cnki.11-1773/v.2022.03.001

2021-10-15；

2022-03-14

国家自然科学基金（U20B200071）

廖学知(1996—)，男，博士研究生，研究方向：飞行器总体设计；（100076）北京9200信箱1分箱.