橡胶隔振器非线性动态特性计算方法研究
杜奕函 胡绍全 杜强
橡胶隔振器非线性动态特性计算方法研究
杜奕函 胡绍全 杜强
(中国工程物理研究院 总体工程研究所,四川 绵阳 621999)
通过正弦扫频试验对橡胶隔振器轴向非线性动态特性进行研究,发现橡胶隔振系统响应具有明显的激振频率相关性。建立了基于FVMS高阶分数导数模型的修正本构模型,并给出隔振系统动刚度和阻尼系数的计算方法,基于非线性最小二乘法原理结合扫频试验结果,识别得到中低频段和共振频段的模型参数,与试验结果比较,所建立的模型能够精确地描述橡胶隔振系统中低频段和共振频段动态特性随激振频率及位移幅值的变化规律,并预测出隔振系统的加速度响应及共振频段的出现,且在其他工况下也具有较好的预测结果,说明建立的模型能够精确地描述橡胶隔振器的轴向动态特性并具有一定的适用性及推广性。
橡胶隔振器;分数导数;非线性本构模型;动态特性
0 引言
振动隔离是工程上解决振动问题的常用手段[1,2]。橡胶材料具有超弹性、易变形等独特的物理和化学特性,常与金属部件结合,用于系统的振动隔离和减振降噪[3]。橡胶隔振器由于结构紧凑、工艺性好、成本低廉等特点,是目前应用最多的一类隔振器。橡胶隔振器的动态力学特性直接影响着隔振效果[4]。实验分析表明,橡胶隔振器的动态特性不仅与温度等条件有关[5,6],还与激振频率及激振位移幅值相关,呈现出明显的频率及幅值非线性。
隔振橡胶材料的粘弹性与其动态力学行为紧密相关,一般采用储能模量、损耗模量和阻尼系数来刻画橡胶隔振系统的动态力学特性[7]。传统的机械模型已被广泛用于描述橡胶隔振器的粘弹性,如Kelvin-Voigt模型、三参数Maxwell模型以及广义Maxwell模型等,这类模型比较直观,但需要辨识的参数多,计算量大[8,9]。在机械模型之后提出的分数导数模型因仅用少量参数就能描述材料的粘弹性以及能反映加载历程对橡胶材料动态特性的影响而备受关注,如分数导数KV模型、分数导数Zener模型以及五参数分数导数模型等[10-14],但这类模型均为最高阶次不大于1的低阶分数导数模型,往往需要改进模型才能较好地吻合实验数据,增加了模型的复杂程度和计算工作量。高阶分数导数模型(参数取不同值时最高阶次大于1)的提出[7,15,16],使得精确描述粘弹性非线性动态力学行为成为可能。然而国内外应用高阶分数导数模型对橡胶材料动态力学行为开展工作还相对较少。无论是使用传统机械模型还是分数导数模型,前人的工作多关注中低频段隔振系统的动态特性,鲜有人研究共振频段的动态特性变化规律。
本文以典型橡胶隔振器为研究对象,在宽频范围内进行轴向正弦扫频试验,分析其中低频段和共振频段的激振频率相关性。建立基于FVMS(fraction Voigt and Maxwell model in series)高阶分数导数模型的修正本构模型,并结合试验结果对模型参数进行识别,将计算结果与传统机械模型以及低阶分数导数模型计算结果进行比较,并进行多工况下动态力学特性的预测,验证所建立的模型能够比较精确地描述橡胶隔振器中低频段和共振频段的动态特性并具有一定的适用性及推广性。
1 橡胶隔振器扫频振动研究
1.1 振动系统的传递函数
当基础做正弦运动时,具有阻尼的多自由度系统的运动方程为
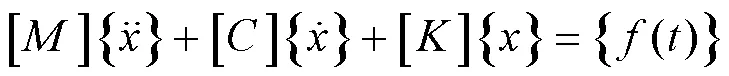
进行坐标变换
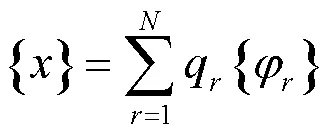
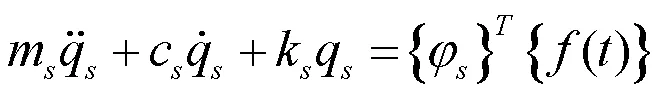

其物理意义为:在点作用单位力时,在点所引起的响应。上述函数关系与激振力的频率有关,称为传递函数,也就是机械导纳。虽然针对加速度、速度、位移的传递函数形式有所差别,但当基础做正弦运动时,三者相对于隔振系统的传递率是相等的[17]。
1.2 扫频试验研究
1.2.1振动参数的设定

1.2.2扫频试验布点
为研究橡胶隔振器轴向动态特性,隔振系统连接结构轴向振动试验方向示意图见图1。图2是试验使用的典型的橡胶隔振器结构图。其中隔振器使用的橡胶材料是三元乙丙橡胶和丁基橡胶的复合橡胶(型号:R-EP/IIR-S001),该隔振器的设计使用寿命是6年。
在安装板上对称布置4个加速度控制点,在试件上布置5个加速度测点,控制点及测点位置见图3和图4。

图1 轴向振动试验示意图

图2 典型的橡胶隔振器
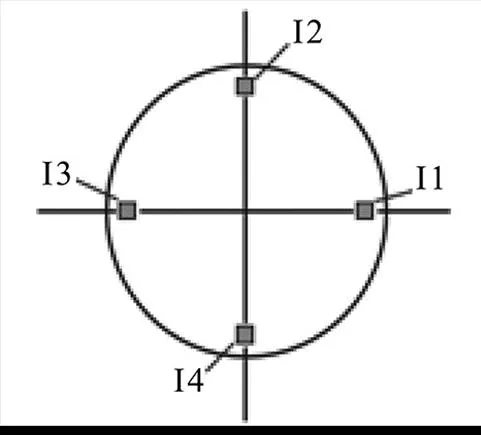
图3 安装板控制点位置
图4 试件测点位置
1.3 幅频响应曲线
在实验室室温条件下对橡胶隔振系统进行20Hz~300Hz范围的正弦扫频试验,扫描速率为1oct/min,振动量级为0.5g、2.0g、4.0g三种量级,采用四点平均控制。以测点A5的响应为例,得到橡胶隔振系统的加速度和振幅放大因子曲线如图5~图6所示。其他测点数据与图5、图6相似。
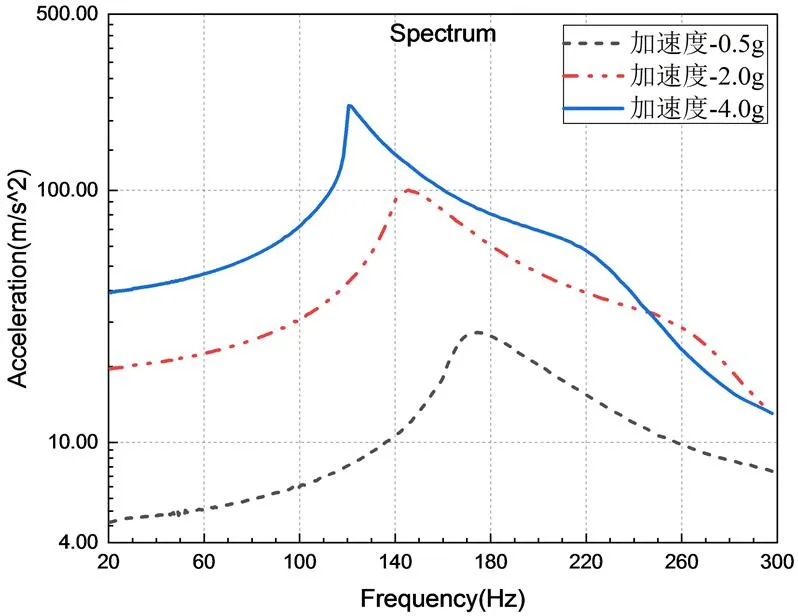
图5 加速度响应曲线
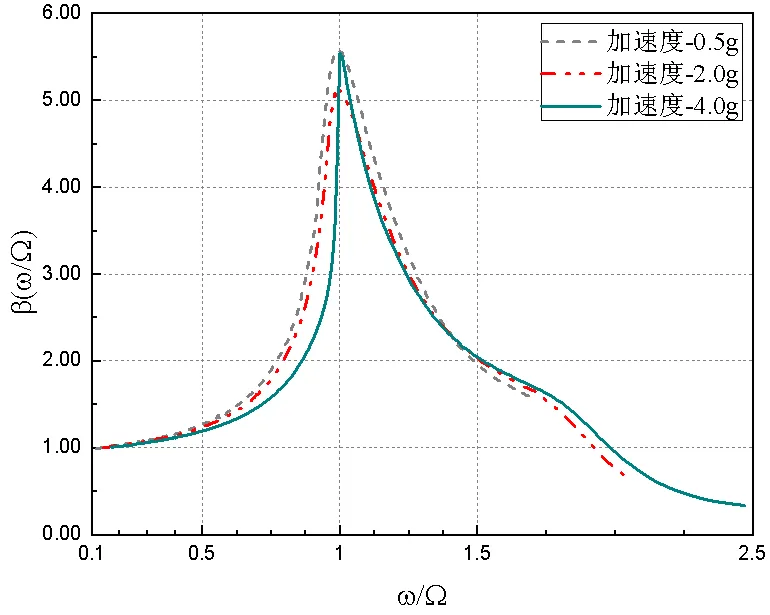
图6 振幅放大因子曲线
通过加速度响应曲线和放大因子曲线可以发现,在20Hz~300Hz频率范围内:1)在激振频率较低时,隔振系统的加速度响应基本等于振动量级,意味着位移响应也基本不变,由此可以得到在不同激振量级下隔振系统的刚度变化在低频基本保持一致;2)同一个频率点下,激振量级不同,激振位移幅值各不相同;3)随着激振量级的增加,振动系统的加速度响应也在增加,固有频率在逐渐减小。但从图6来看未见橡胶隔振系统呈现出明显的幅值非线性。表明橡胶隔振系统动态力学行为呈现出明显的频率非线性。温度条件对于橡胶隔振器的动态力学特性有一定影响[5,6,11],本文在进行试验时室温维持在23℃~25℃,在后续分析工作中暂不考虑温度因素的影响。
1.4 动刚度和阻尼系数的计算
1.4.1阻尼比
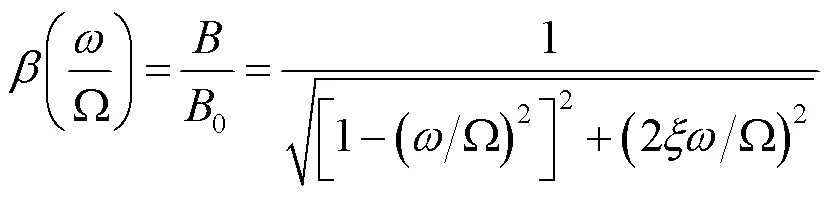
1.4.2 动刚度
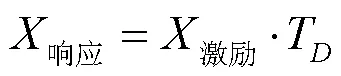
得到隔振系统响应位移如图7所示。已知激振量级、系统质量的情况下,可以计算出系统受到的激振力,并根据动刚度等于激振力与系统响应位移的比值关系
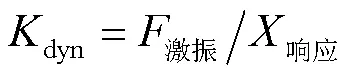
得到隔振系统动刚度随频率变化如图8所示。
选取频率点90Hz到240Hz为共振频段,在此频段之前为中低频段。从图7可以得到,在20Hz~300Hz频率范围内,对于正弦扫频试验,在振动量级一定的情况下,响应位移随着激振频率的增加而减小,在共振区附近出现极大值,经过共振区后随着频率的增加持续减小。图8说明在20Hz~300Hz频率范围内,振动量级一定时,隔振系统的动刚度在中低频段随着频率的增加而增加,到达共振区附近开始减小出现极小值,这很好地解释了共振区响应传递率出现极大值的原因,刚度减小,系统的变形增大,而后动刚度随着频率的增大持续增加。
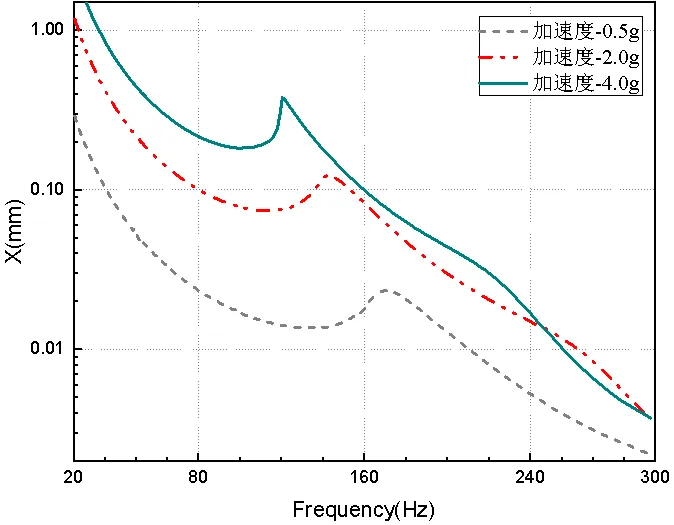
图7 不同振动量级隔振系统的响应位移
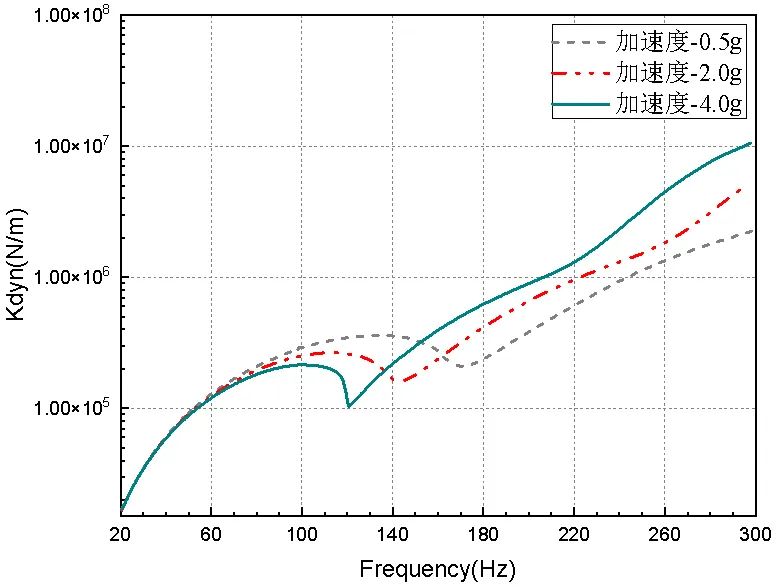
图8 不同振动量级动刚度随频率变化
1.4.3阻尼系数
根据1.4.1节计算出的阻尼比随频率变化如图9所示,又因为
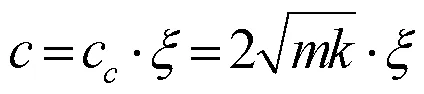
由此计算出隔振系统的阻尼系数如图10所示。
从图9可以得到,阻尼比在激振频率远离共振区域即在中低频率范围内,随着频率的增加而减小,在激振频率经过共振区时基本保持不变并出现不明显的极大值,之后随着频率的增加继续减小。
阻尼系数的变化与阻尼比类似。从激振频率较低时,响应位移产生,阻尼系数随着频率的增加而增加。当靠近共振区域时开始减小,经过共振区域出现极大值,这与隔振器响应位移变化趋势相符合,当系统振动以后,在响应位移逐渐减小时,高分子橡胶结构自身的摩擦力在减小导致阻尼系数减小。在高频段响应位移逐渐减小,此时阻尼已不再起主要控制作用。
综上所述,隔振系统的非线性特性表现为动刚度和阻尼系数呈现明显的激振频率非线性,本文采用高阶分数导数本构模型对动刚度和阻尼系数的非线性特性进行预测。
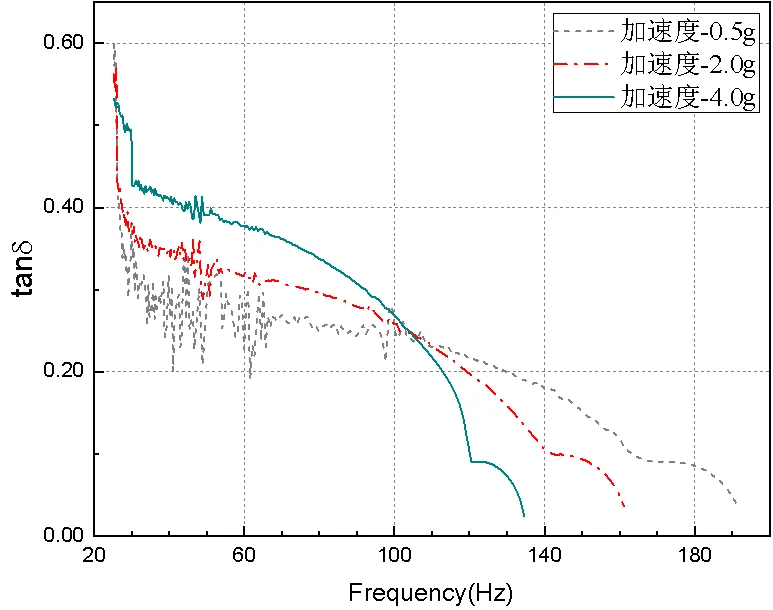
图9 不同振动量级阻尼比随频率的变化

图10 不同振动量级阻尼系数随频率的变化
2 高阶分数导数本构模型
本文通过分数导数Maxwell和分数导数KV模型串联得到的FVMS(fraction Voigt and Maxwell model in series)[7,15]高阶分数导数模型对隔振系统非线性力学行为做出描述及预测。
2.1 FVMS高阶模型
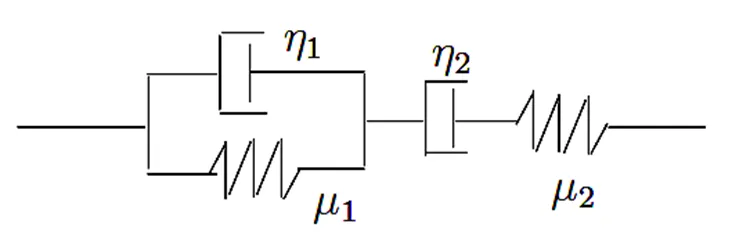
图11 FVMS高阶分数导数模型
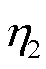
2.2 复刚度与阻尼系数推导
根据图11,结合应力应变串并联关系
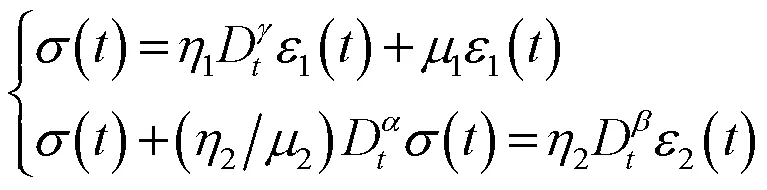
同时有
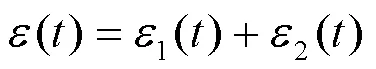
得到力-位移关系为

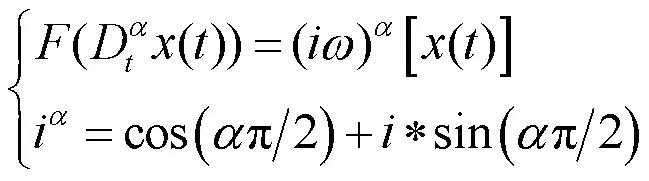
进行频域与时域的变换,分离实部与虚部可以计算得到动刚度实部、虚部和损耗因子,从而计算出隔振系统的动刚度,其过程稍显繁琐,本文不再赘述。复刚度与损耗因子表示为

阻尼比与材料力学损耗因子之间存在如下关系
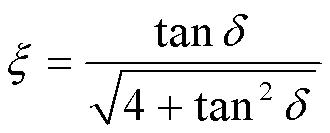
结合式(9)进而计算出隔振系统的阻尼系数。
3 橡胶隔振器动态特性分析
3.1 中低频段分析
3.1.1 模型修正与参数识别
激励频率在20Hz~60Hz范围内,隔振系统动刚度在不同振动量级下基本保持一致,90Hz以后开始接近共振区域,因此先选取振动量级0.5g,2g,4g三种工况下60Hz~90Hz试验数据进行参数识别。分数导数阶数基于非线性最小二乘法拟合初始参数如表1所示。

表1 中低频段分数导数阶数参数识别结果
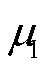
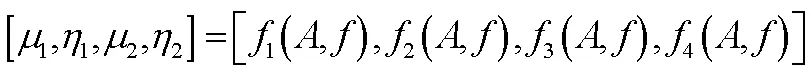
结合试验结果,使用二次多项式拟合各参数与振动量级、激励频率之间的关系
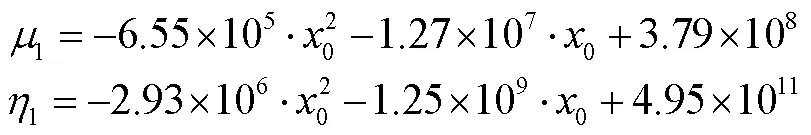
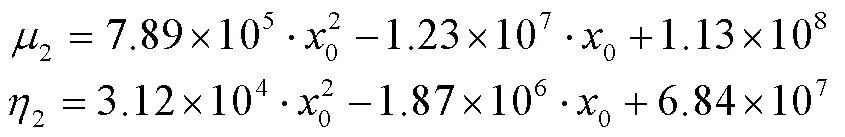
3.1.2中低频段不同模型计算结果对比
以振动量级0.5g正弦激励工况为例,将基于修正的FVMS高阶模型计算结果与其它模型计算结果进行对比,如图12~图15所示。
从图12~图15可以看出,传统的粘弹性模型和低阶分数导数模型只能在比较小的频率范围内与试验结果相接近,但在大部分频率区域,拟合结果与试验数据相去甚远。而基于修正的高阶分数导数模型可以在较宽频率范围内与试验结果相吻合,这充分体现了高阶分数导数粘弹性模型的优势,说明了利用FVMS高阶模型来预测粘弹性材料的动力学响应是比较精确的,有助于后续工作的开展。
3.1.3多工况中低频段预测结果
基于修正的FVMS高阶分数导数模型进行三种振动量级60 Hz~90 Hz频率范围正弦激励工况计算(取一半频率点),结果如图16~图17所示。
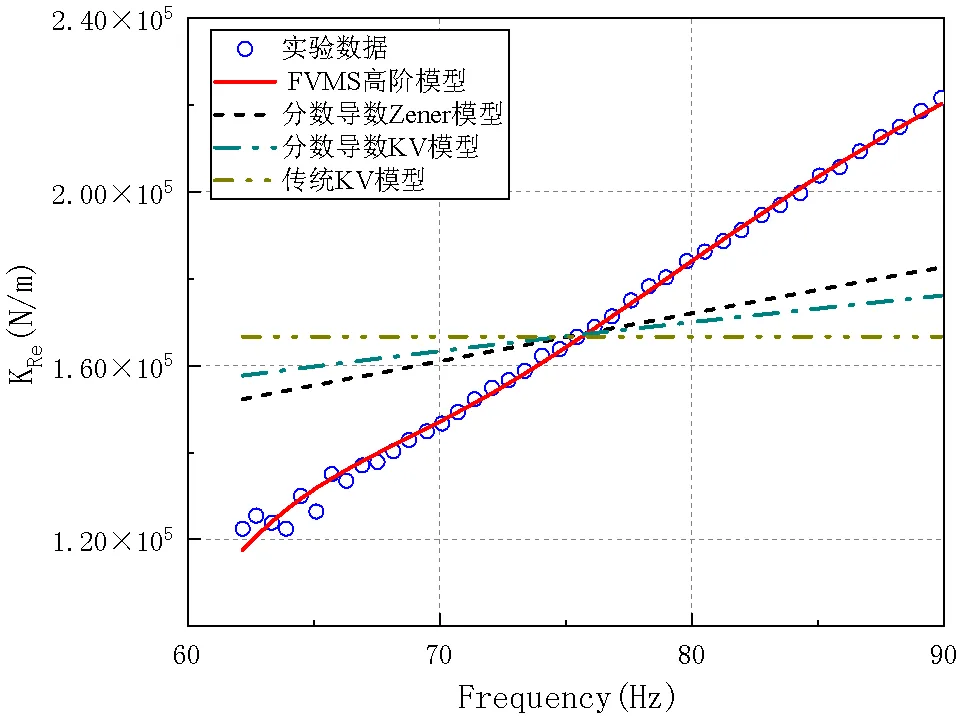
图12 振动量级0.5g动刚度实部预测值
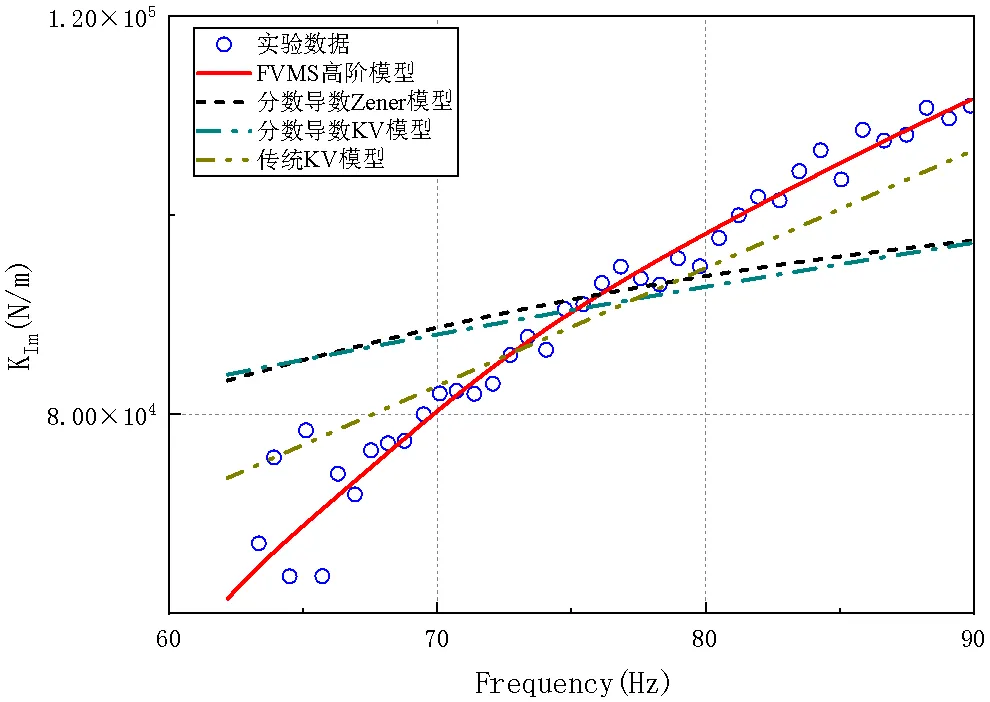
图13 振动量级0.5g动刚度虚部预测值
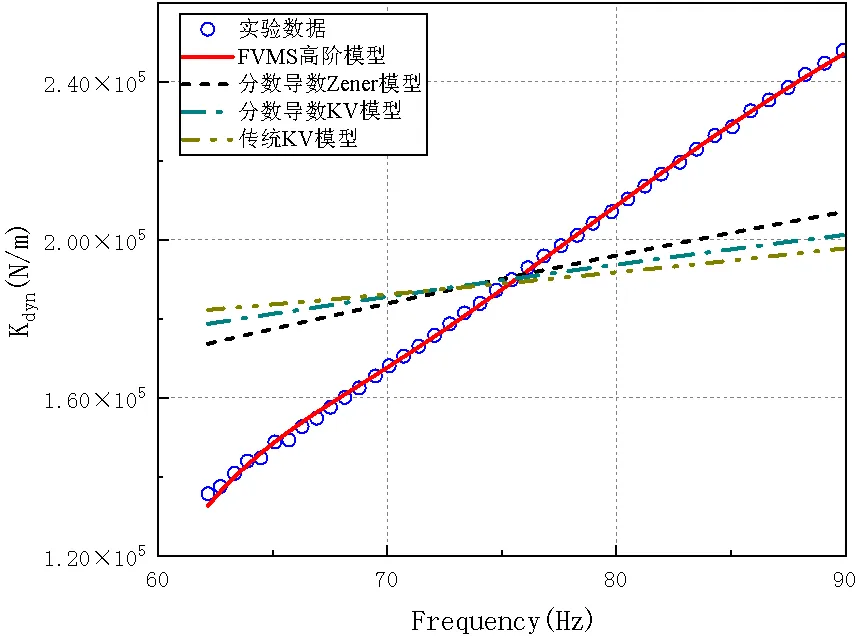
图14 振动量级0.5g动刚度预测值
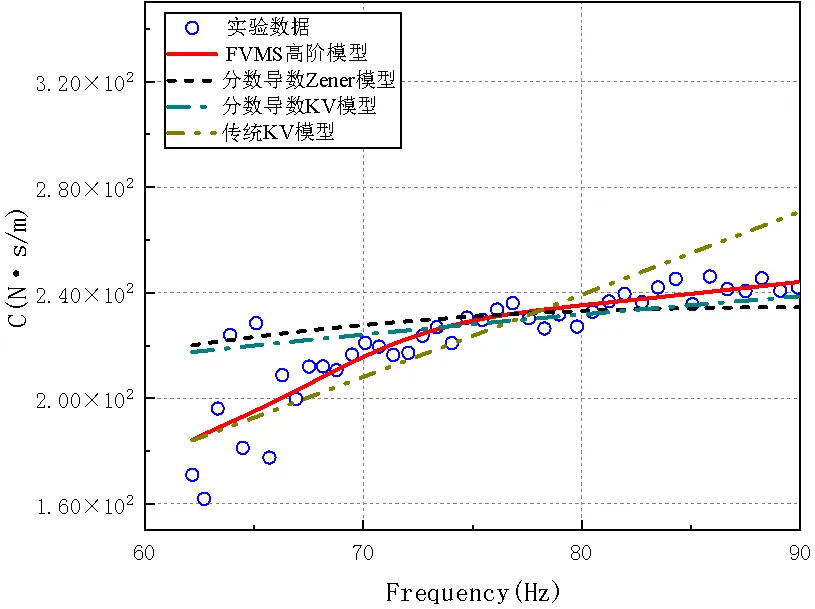
图15 振动量级0.5g阻尼系数预测值
从图16~17可以看出,修正的分数导数高阶模型对于预测三种工况中低频范围内的动态特性效果较好,能描述出动刚度和阻尼系数在中低频范围内随着激振频率增加的变化规律。动刚度预测结果比较精准,误差控制在5%以内,而阻尼系数计算的误差相较于动刚度偏大,这可能是由于预测动刚度实部、虚部精确度不够造成的。
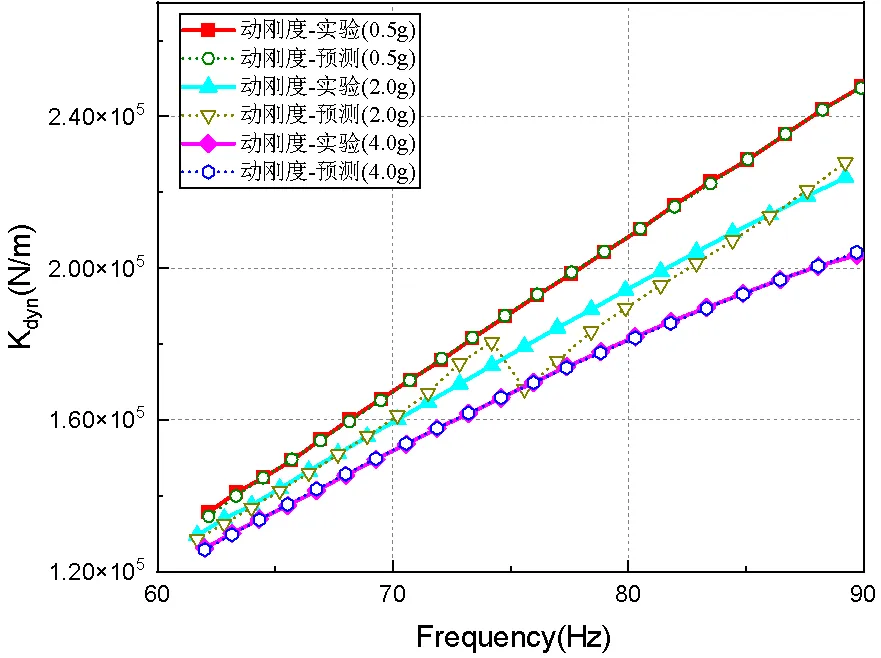
图16 中低频段多工况动刚度预测值
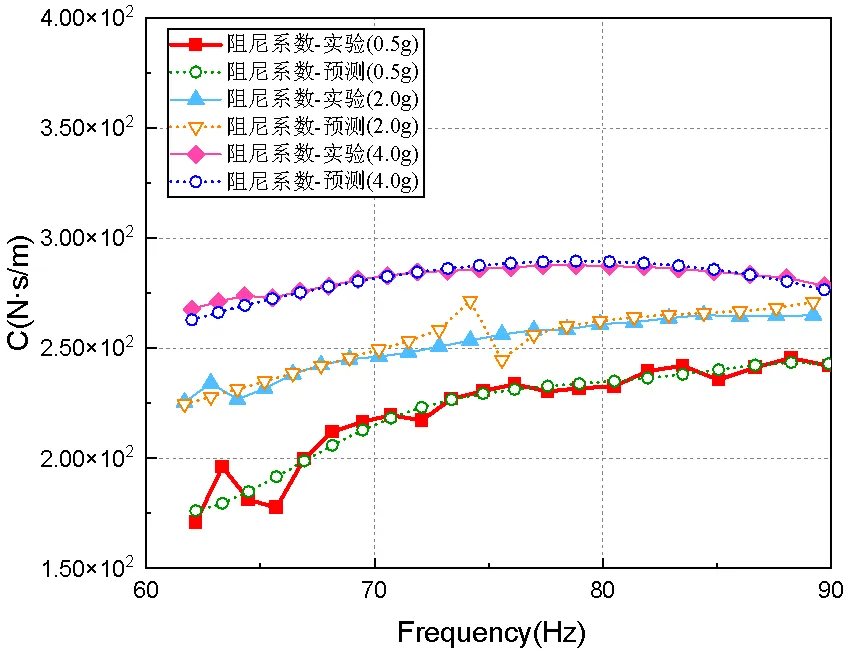
图17 中低频段多工况阻尼系数预测值
3.2 共振频段分析
共振区域的振动响应是造成振动危害的主要原因之一,预测出共振区域的动态特性变化对于振动危害的防护十分重要。
3.2.1参数识别
选取振动量级0.5g,2g,4g三种工况下共振频段试验数据进行参数识别。基于非线性最小二乘法拟合初始参数结果如表2所示。

表2 共振段分数导数阶数参数识别结果
共振段分数导数系数识别结果
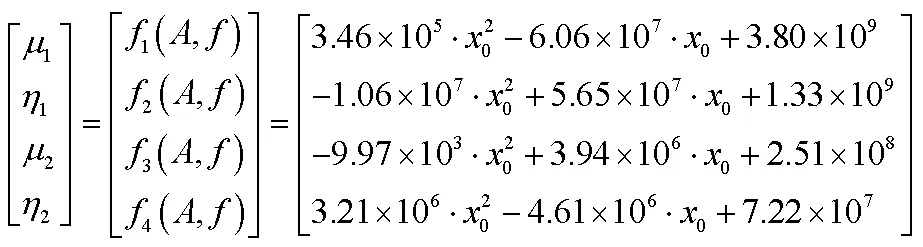
3.2.2共振频段动态特性预测结果
三种振动量级不同工况下的动刚度、阻尼系数计算结果如图18~图19所示。由图18~图19可知,在接近共振区域时,曲线较平滑,拐点较少,预测结果比较准确。在经过共振区域时,动刚度和阻尼系数出现拐点,预测结果有一定偏差。但计算曲线能较好地反映动刚度和阻尼系数在靠近共振段之前随频率增加/减小,在经过共振区域时出现极小/大值的现象,说明基于修正的FVMS高阶分数导数模型能较好地预测此类橡胶隔振器的动态特性并具有较高的预测精度。
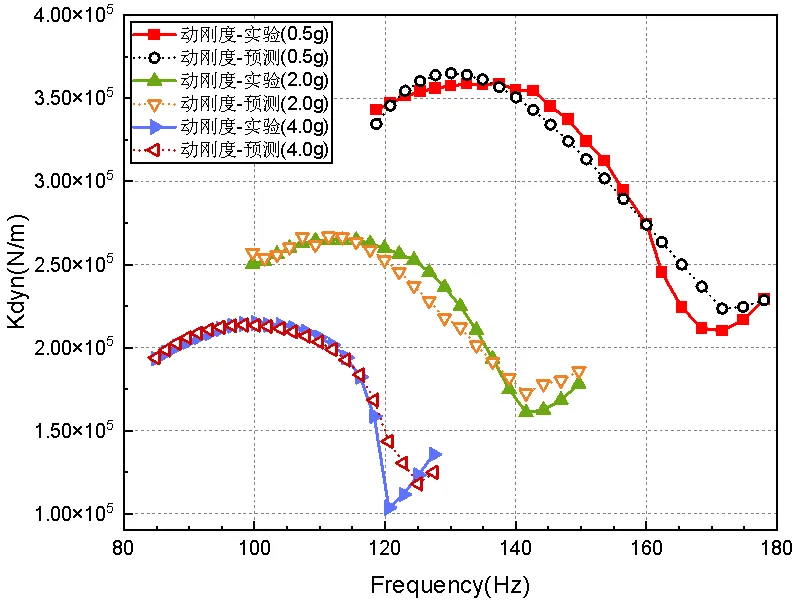
图18 共振频段多工况动刚度预测值
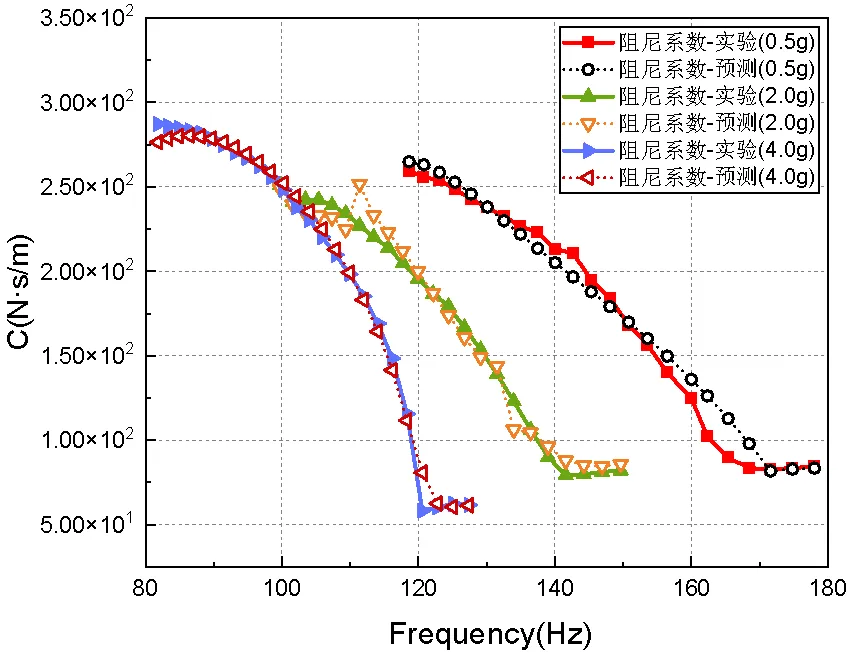
图19 共振频段多工况阻尼系数预测值
3.3 频响曲线预测
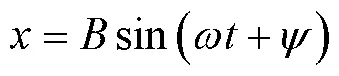
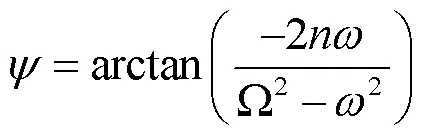
将之前计算得到的动刚度、阻尼系数带入(22)式,得到系统在0.5g、2.0g、4.0g三种振动量级下的加速度响应预测如图20所示。
图20 多工况系统加速度响应预测
Fig.20 Acceleration response prediction for multi-case systems
从图20可看出,前文计算的数据能够较好地预测出振动系统的加速度响应曲线,说明基于修正的FVMS高阶分数导数模型对于预测橡胶隔振器的系统响应具有较高的精度,并且能够反映振动系统共振区的力学特性及预测共振频段的出现。
3.4 模型其他工况预测
基于修正的FVMS高阶分数导数模型,以3.2节中三种工况下识别出的初始参数对橡胶隔振器在振动量级1.0g、8.0g工况下中低频段和共振频段的动态特性进行模型外推与内插验证计算,如图21~图22所示。从图21~图22可以看出所建立的模型对于其他工况的动态特性预测结果有一定误差,但整体精度较高,能够较好地描述出隔振系统的动刚度和阻尼系数随激振频率及激励位移幅值变化之间的关系,说明所建立的模型具有一定的适用性。并可以得到如图23所示的幅频响应曲线预测图。

图21 其它工况动刚度预测值

图22 其它工况阻尼系数预测值
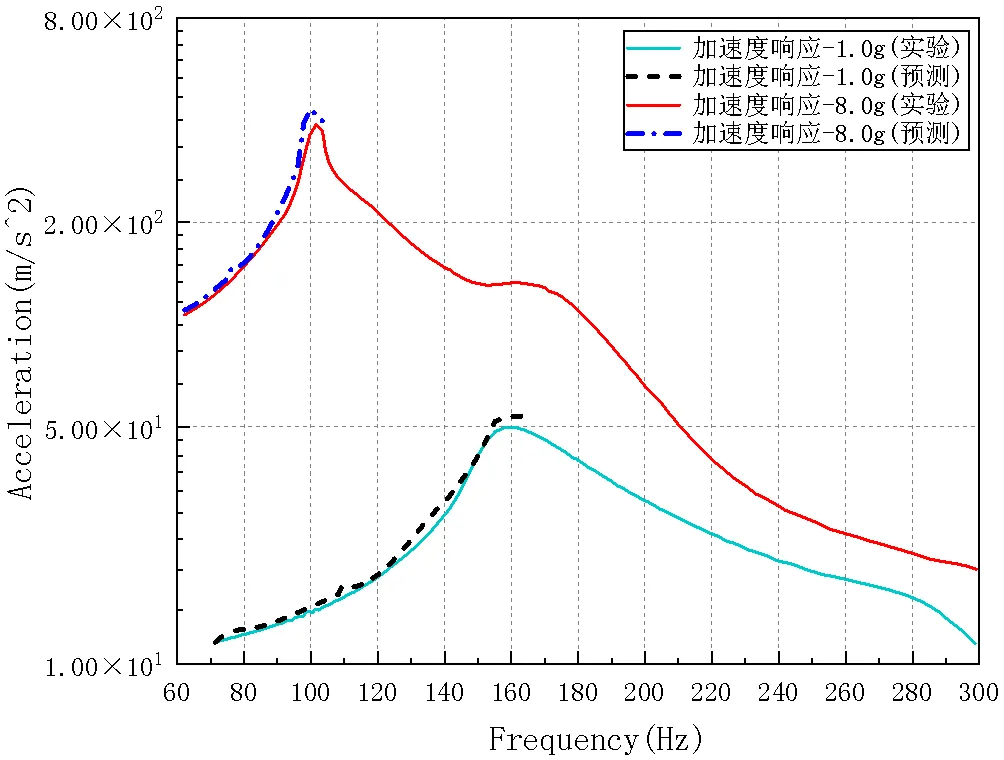
图23 其它工况系统响应预测
4 结论
1)以某橡胶隔振器为载体,构造典型隔振系统,通过正弦扫频试验发现隔振系统动刚度、阻尼系数与激振频率、激振位移幅值有关,其动态力学行为呈现出明显的频率非线性。
2)建立了基于FVMS高阶分数导数模型的修正本构模型,并给出了动态刚度和阻尼系数的计算方法,与传统的粘弹性本构模型及低阶分数导数模型进行对比,发现本文所建立的模型在中低频段、共振频段均具有较高的预测精度。在振动量级0.5 g、2.0 g、4.0 g三种工况下进行参数识别,所建立的模型能够较好地预测隔振系统动态特性随激振频率及位移幅值的变化规律。
3)基于模型计算得到的动态刚度及阻尼系数,解出了隔振系统的幅频响应曲线并与试验结果进行比较,发现所建立的模型及采用的计算方法能够较好地预测橡胶隔振器的加速度响应。
4)本文所建立的模型具有较高的整体预测精度及一定的适用性和推广性。
[1] 李东海, 赵寿根, 何玉金, 等. 正负刚度并联准零刚度隔振器的静态特性研究[J]. 强度与环境, 2017, 44(6): 31-36. [LI Donghai, Zhao Shougen, He Yujin, et al. Study on static characteristic of a quasi-zero-stiffness vibration isolator of positive and negative stiffness in parallel[J]. Structure & Environment Engineering, 2017, 44(6): 31-36.]
[2] 张佳琪, 熊学文, 周巍峰, 等. 基于被动隔振平台的振动主动控制研究[J]. 强度与环境, 2019, 46(4): 25-30. [Zhang Jiaqi, Xiong Xuewen, Zhou Weifeng, et al. Research on active vibration control based on passive vibration isolation platform[J]. Structure & Environment Engineering, 2019, 46(4): 25-30.]
[3] 周振凯, 徐兵, 胡文军, 等. 橡胶隔振器大变形有限元分析[J]. 振动与冲击, 2013, 32(5): 171-175. [Zhou Zhenkai, Xu Bing, Hu Wenjun, et al. Large deformation finite element analysis of rubber isolator[J]. Journal of Vibration and Shock, 2013, 32(5): 171-175.]
[4] 林松, 张鲲, 孙磊, 等. 橡胶隔振器动态特性的本构研究[J]. 振动与冲击, 2011, 30(3): 177-179, 210. [Lin song, Zhang Kun, Sun Lei, et al. Study on dynamic characteristics of rubber isolator [J]. Journal of Vibration and Shock, 2011, 30(3): 177-179.]
[5] 刘迪辉, 范迪, 欧阳雁峰, 等. 温度对橡胶隔振器力学性能的影响[J]. 噪声与振动控制, 2014, 34(3): 203-206. [Liu Dihui, Fan Di, OuYang Yanfeng, et al. Temperature effect on mechanical properties of rubber isolators [J]. Noise and Vibration Control, 2014, 34(3): 203-206.]
[6] 韦子祥, 邱中辉, 王旦, 等. 温度对橡胶隔振器刚度阻尼特性的影响[J]. 机械与电子, 2022, 40(2): 23-28. [Wei Zixiang, Qiu Zhonghui, Wang Dan, et al. Effects of temperature on the stiffness damping characteristics of the rubber vibration isolator [J]. Machinery & Electronics, 2022, 40(2): 23-28.]
[7] 赵永玲, 侯之超. 基于分数导数的橡胶材料两种粘弹性本构模型[J]. 清华大学学报(自然科学版), 2013, 53(3): 378-383. [Zhao Yongling, Hou Zhichao. Two viscoelastic constitutive models of rubber materials using fractional derivations [J]. Journal of Tsinghua University(Science and Technology), 2013, 53(3): 378-383.]
[8] 潘孝勇, 上官文斌, 柴国钟, 等. 橡胶隔振器动态特性计算方法的研究[J]. 振动工程学报, 2009, 22(4): 345-351. [Pan Xiaoyong, ShangGuan Wenbin, Chai Guozhong, et al. An investigation of calculation methods for the dynamic characteristics of rubber isolator [J]. Journal of Vibration Engineering, 2009, 22(4): 345-351.]
[9] 吴杰, 上官文斌, 潘孝勇. 采用超弹性-粘弹性-弹塑性本构模型的橡胶隔振器动态特性计算方法[J]. 机械工程学报, 2010, 46(14): 109-114. [Wu Jie, ShangGuan Wenbin, Pan Xiaoyong. Computational method for dynamic properties of rubber isolators using hyperelastic-viscoelastic-plastoelastic constitutive model [J]. Journal of Mechanical Engineering, 2010, 46(14): 109-114.]
[10] T Pritz. Five-parameter fractional derivative model for polymeric damping materials[J]. Journal of Sound and Vibration, 2003 (5): 935-952.
[11] 林松, 高庆, 李映辉, 等. 一种考虑宽温宽频宽动态位移的粘弹性本构模型[J]. 航空动力学报, 2007, 22(3): 431-438. [Lin Song, Gao Qing, Li Yinghui, et al. A viscoelastic constitutive model under broad temperature frequency and dynamic displacement [J]. Journal of Aerospace Power, 2007, 22(3): 431-438.]
[12] 唐振寰, 罗贵火, 陈伟, 等. 橡胶隔振器黏弹性5参数分数导数并联动力学模型[J]. 航空动力学报, 2013, 28(2): 275-282. [Tang Zhenhuan, Luo Guihuo, Chen Wei, et al. Parallel dynamic model of rubber isolator about five-parameter fractional derivatives [J]. Journal of Aerospace Power, 2013, 28(2): 275-282.]
[13] 赵永玲, 侯之超, 黄友剑, 等. 橡胶材料的一种5参数分数导数模型[J]. 振动与冲击, 2015, 34(23): 37-41.[Zhao Yongling, Hou Zhichao, Huang Youjian, et al. A fractional derivative model with five parameters for rubber materials [J]. Journal of Vibration and Shock, 2015, 34(23): 37-41.]
[14] Fanjing Meng, Jin Hui. Slope Shift Strategy for Automatic Transmission Vehicles Based on the Road Gradient[J]. International Journal of Automotive Technology, 2018, 19(3): 509-521.
[15] JG Liu, Xu MY. Higherorder fractional constitutive equations of viscoelastic materials involving three different parameters and their relaxation and creep functions [J]. Mechanics of Time-Dependent Materials, 2006, 10(4): 263-279.
[16] 高琦, 冯金芝, 郑松林, 等. 橡胶衬套高阶分数导数动力学模型的研究[J]. 汽车工程, 2019, 41(8): 872-879. [Gao Qi, Feng Jinzhi, Zheng Songlin, et al.A study on higher-order fractional derivative dynamic model of rubber bushing [J]. Automotive Engineering, 2019, 41(8): 872-879.]
[17] 程贺章. 金属橡胶的静态特性及其减振机理研究[D]. 哈尔滨工程大学, 2015. [Cheng Hezhang. Research on of static characteristics and vibration isolation mechanism of metal rubber material[D]. Harbin Engineering University, 2015.]
Study on Computing Method of Nonlinear Dynamic Characteristics of Rubber Isolator
DU Yi-han HU Shao-quan DU Qiang
(Institute of Systems Engineering, China Academy of Engineering Physics, Mianyang 621999,China)
The axial nonlinear dynamic characteristics of the rubber isolator are investigated by means of sinusoidal frequency sweep tests, and it is found that the response of the rubber isolation system has a significant excitation frequency dependence. A modified principal structure model based on the higher-order fractional derivative model of the FVMS is established, and the dynamic stiffness and damping coefficients of the vibration isolation system are calculated. The model can accurately describe the dynamic characteristics of the rubber isolation system in the low frequency and resonant frequency bands with the frequency and displacement amplitude, and predict the acceleration response of the vibration isolation system and the occurrence of the resonant frequency band, and also has good prediction results in other operating conditions, It shows that the model developed can accurately describe the axial dynamic characteristics of the rubber isolator and has certain applicability and extension.
Rubber isolator; Fractional derivative; Nonlinear constitutive model; Dynamic characteristics
TB535.1
A
1006-3919(2022)03-0036-09
10.19447/j.cnki.11-1773/v.2022.03.006
2022-02-19;
2022-5-20
国家自然科学基金面上项目(11872059)
杜奕函(1998—),男,硕士研究生,研究方向:结构动力学;(621999)四川省绵阳市919信箱419分箱.

