旋转失效卫星的运动观测及消旋接触方案设计
藏 悦,胡 权,张 尧,安 泉,王鸿博
(北京理工大学宇航学院,北京 100081)
0 引 言
失效卫星等空间非合作目标的在轨清除技术是缓解空间轨道资源紧缺、降低卫星在轨运行风险的重要手段。但是目标的非合作特性使得其状态信息难以获取,并且空间中的长期扰动导致其运动状态复杂未知。所以,非合作目标的在轨清除任务难度大、风险高。对一类快速旋转的失效卫星,为了安全有效地实施在轨清除,首先需要采取有效手段降低其旋转速度,以降低后续操作难度和风险。在针对快旋失效卫星的消旋研究中,机械臂接触式消旋具有操作精度较高、消旋作用较强等优点,应用价值较高,是目前研究的热点。但现有研究大多着力于分析碰撞接触带来的消旋效果和相应的动力学与控制问题,较少考虑开展接触消旋之前对旋转目标的信息测量与接触策略设计过程。然而机械臂在接触旋转失效卫星时,面临无效操作、意外碰撞等风险,通过视觉观测获取失效卫星的几何与运动等信息,并设计合理有效的消旋方法,能够有效降低接触风险、提高消旋效率,完善失效卫星在轨清除的操作环节。
视觉测量技术在非合作目标的运动辨识方面应用广泛。胡启阳等使用双目视觉,分别设计非合作目标的姿态测量和相对导航滤波器,实现了目标质惯量、运动状态和轨道参数的高精度辨识。郭新程等在近距离观测且目标运动模型已知的条件下,通过单目相机识别非合作翻滚目标的固有特征,结合卡尔曼滤波算法估计了目标的惯量比和运动状态。Dong等结合了光流算法和扩展卡尔曼滤波,用单目相机实现了静态和动态目标的位姿运动估计。郝刚涛等针对空间翻滚目标存在先验信息不足和模型不确定性等问题,提出一种基于视觉同步定位与建图的相对位姿估计方法,但该方法计算量大,不便于实时解算。以上研究都结合滤波方法,求解了各时刻相机与目标之间的相对位姿,但对于快速旋转目标,在消旋方法设计阶段更加注重对目标角速度的辨识,而不必持续求解相对位姿。寇鹏等对高速翻滚空间目标的雷达散射截面序列进行了形态学运算和经验模态分解,并结合本征模态函数谱分析和非参数检验分组求秩,获得了较高精度的目标翻滚周期,相比滤波求解相对位姿,所求参数更加简明,计算量较小。
为了安全地实现接触式消旋,还需要结合目标几何外形,设计机械臂接触方法。许多学者从分析操作目标特性和机械臂运动规划的角度,研究了运动目标的消旋和抓捕方法。Lampariello等依据长时间仿真结果,分析旋转目标上抓捕点的运动规律,在确保机械臂工作空间能覆盖捕获点运动区域的基础上,有针对性地进行机械臂非线性运动规划。Xu等对旋转目标的捕获问题,提出了抓捕区域的概念并设计了双机械臂的接近轨迹,使末端作动器垂直接触抓捕区域并形成双臂合抱,成功捕获了旋转目标,相比抓捕目标上固定点,合抱方式提升了抓捕效率。Peng等在估计目标的运动和惯量后,分析了旋转目标中心体两侧的抓捕点运动轨迹,并据此规划了双臂协同捕获操作的运动轨迹,以实现对旋转目标的有效捕获。以上研究大都分析了目标上预设抓捕点或区域的运动规律,并据此开展机械臂运动规划,但对于无法预设接触点的非合作目标,则需要分析目标表面的运动包络,选取适宜接触的区域,以设计合理的接触消旋方法。
本文以旋转失效卫星为消旋目标,在对目标序列观测图像的处理中,提出了一种双重光流约束的特征点运动跟踪识别方法,用于求解失效卫星的旋转角速度、分析适宜接触区域,并服务于接触式消旋操作的方案设计。首先,建立服务航天器与失效卫星组成的消旋系统并给出视觉测量模型,通过双目视觉持续观测旋转失效卫星。基于光流法与立体视觉原理,设计迭代式双重光流约束算法,获取目标表面特征点的运动轨迹。通过对轨迹的频域分析求解失效卫星的角速度,并结合特征点的空间运动规律给出失效卫星表面适宜接触区域。在约束双臂接触消旋时间的条件下,给出完成消旋的接触强度需求,为机械臂接触式消旋操作的任务规划和控制系统设计提供参考。
1 旋转失效卫星的接触消旋系统模型
在本研究中,服务航天器上安装有两部七自由度机械臂,可在接近旋转失效卫星后执行接触消旋操作。接触消旋系统如图1所示。服务航天器的基座上安装有双目立体视觉测量装置,在机械臂开展消旋操作之前观测目标,获取目标的几何外形和运动状态,用于设计接触消旋方法,并作为测量装置辅助执行消旋操作。
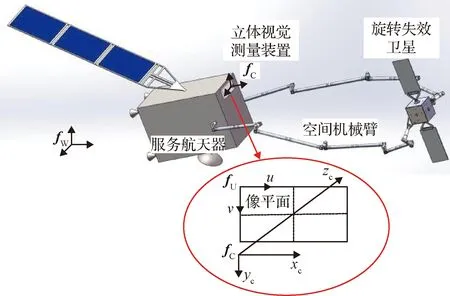
图1 旋转失效卫星接触消旋系统Fig.1 The contact-detumbling system for a rotating failed satellite
视觉测量模型描述了相机图像与现实世界中物体的转换关系,用于从图像中还原现实世界物体的几何与运动。采用传统的小孔透射相机模型,定义世界坐标系{},相机坐标系{}和像素坐标系{},惯性空间中的某一观测点P在世界坐标系下的坐标(,,)与相机坐标系下的坐标(,,)以及在像素坐标系中的坐标(,)之间的关系为

(1)


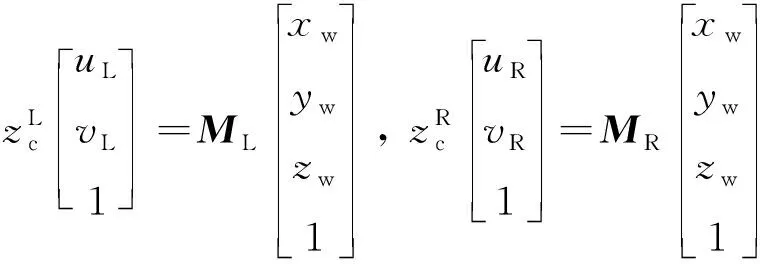
(2)
式中:和分别表示左右相机的投影矩阵。
联立左右相机的观测方程,可根据像素位置坐标解得观测点在世界系下的三维位置坐标。
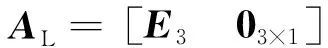
2 旋转失效卫星特征点跟踪识别
在观测非合作的旋转失效卫星时,由于无法预测图像中识别特征点的分布与位置,难以求解相对姿态,但通过对相同特征点的运动跟踪能够间接获知目标的运动。KLT算法(Kanade-Lucas-Tomasi tracking)是一种常用的基于光流的观测目标跟踪算法,该算法通过寻找帧间图像中特征角点灰度差平方和最小的偏移量,实现了相同特征点的匹配。
在双目持续观测的条件下,本文依据KLT算法,设计了一种双重光流约束的特征点运动跟踪识别方法,具体步骤如下:
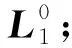


(4) 判断是否继续观测,在继续观测的情况下,读取新一帧(第帧)双目相机图像;

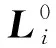

重复第(4)至(7)步,直到达到预设观测时长,即完成总帧数帧的观测后,停止视觉观测。观测流程如图3所示。
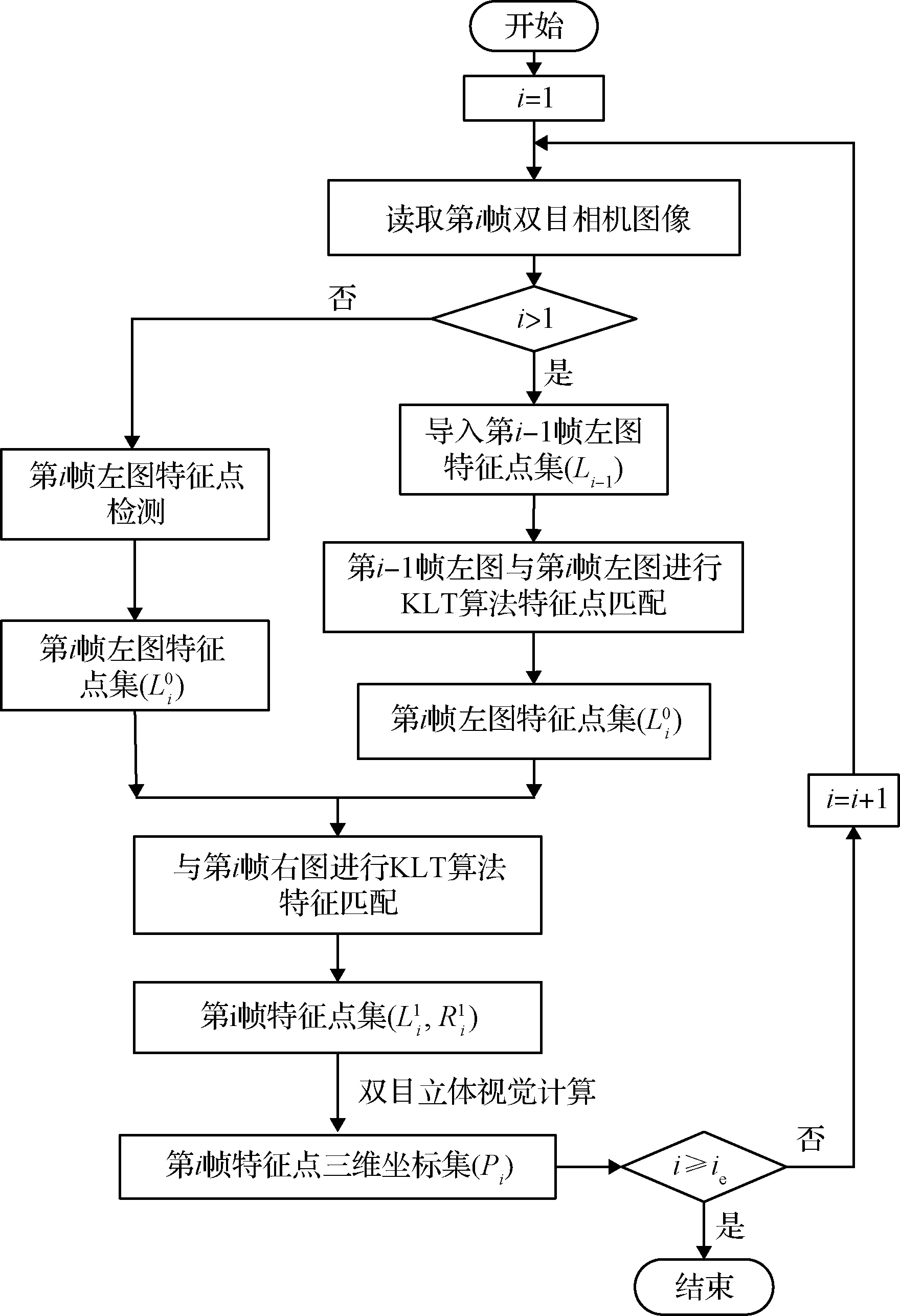
图2 稳定跟踪识别特征点的三维坐标集求解流程Fig.2 Solving process of 3D coordinate set for stable tracking and identifying feature points
在稳定跟踪识别特征点的三维坐标集求解过程中,每一轮迭代两次使用KLT算法进行特征点匹配,即双重光流约束。第一次匹配筛选出时间序列上前后两帧图像中能够稳定跟踪识别的特征点,表征特征点在视野中的稳定存在;第二次匹配则使用同一时刻的双目图像,筛选出能够得到三维位置信息的特征点对的集合,并依据已知的双目相机参数,求解特征点的三维位置坐标集。重复上述步骤,便可得到具有时间标签的稳定跟踪识别特征点的三维坐标序列,即特征点运动轨迹。
为验证所提特征点跟踪识别算法的有效性,在实验室条件下搭建地面物理仿真系统。将带有两个太阳帆板的立方体目标视作待观测的失效卫星,并将其置于单轴恒定速率转台上,采用ZED双目相机观测其运动,相关参数见表1。
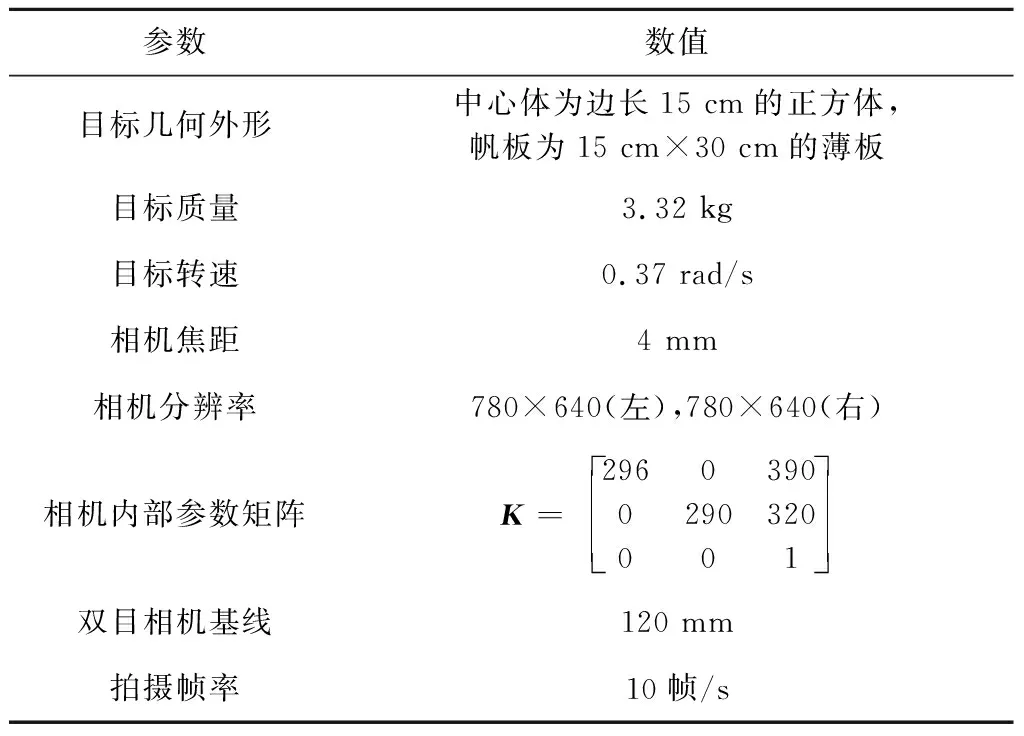
表1 地面物理实验参数Table 1 Ground-based physical experiment parameters
在持续观测100 s过程中,部分特征点因目标旋转而被遮挡,导致稳定跟踪识别的特征点个数逐渐衰减,从第一帧图像的=998衰减至第1000帧图像的=8,在第3, 150和400帧的左相机图像中,稳定跟踪识别的特征点分布情况如图3。由于目标旋转运动同时改变了图像中目标的状态和目标上相同位置的光照情况,使得特征点的跟踪识别受到较大扰动,在前30帧中的观测中特征点数量衰减较快,此后仍然能被稳定跟踪识别的特征点则相对相机具有相对稳定的运动状态和光照条件,其轨迹对目标运动状态的分析具有重要作用。

图3 稳定跟踪识别特征点分布变化Fig.3 The distribution of feature points that can be stably tracked and identified
绘制能够稳定跟踪识别超过50帧的210个特征点轨迹如图4,轨迹阶梯状分布并呈现扇形,反映出目标的运动包络和旋转轴所在位置。此外,卫星旋转轴附近区域的特征点点迹分布密集,存在大量能够长时间稳定跟踪识别的特征点,形成的轨迹基本处于同一平面上,共有31个特征点能够稳定跟踪识别超过500帧图像,放大图展示了其中3个特征点的轨迹,可知轨迹大致呈螺旋状,反映出目标近似单轴旋转的运动状态。
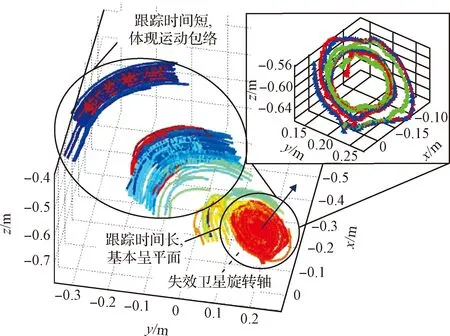
图4 稳定跟踪识别特征点轨迹Fig.4 Trajectories of feature points that can be stably tracked and identified
总体而言,跟踪时间较短的特征点点数更多,所形成的轨迹更能反映出目标的几何外形与运动包络,而能够长时间跟踪的特征点,其轨迹则更加有利于分析目标的运动形式。
实验中用于双目相机图像处理和特征点轨迹记录的上位机配置有主频为2 GHz的Ryzen 5处理器、频率2400 Hz的8 GB内存,处理1000帧图像共计用时114.5 s。其中,第一帧图像需要对全图进行特征点识别,用时0.35 s,之后每帧图片的处理中,由于采用本文所提的双重光流约束的特征点运动跟踪识别方法,减小了图像处理的计算量,每帧图片处理的平均用时可缩减到0.11 s,计算效率较高,可应用于工程实践中。
3 旋转失效卫星的角速度测量
失效卫星在长期运动演化后,由于存在能量耗散,通常绕最大惯量主轴稳定旋转,且角速度基本保持不变。本研究中认为失效卫星处于这一运动状态,依据稳定跟踪识别特征点的轨迹,求解目标绕最大惯量轴的角速度。
从图3和图4可知,稳定跟踪识别的特征点在目标上的分布随时间变化且难以预判,但是在目标旋转的作用下,特征点大致呈匀速圆周运动并形成近似圆弧的轨迹。曲线拟合的方法虽然能够获得特征点的运动半径与目标旋转角速度,但容易受观测精度和图像处理随机误差的影响,难以保证求解的准确性。因此以特征点到左相机的距离,即特征点位置矢量的模||为输入信号,采用快速傅里叶变换(Fast Fourier transform, FFT)方法分析||的频谱特征,从而求出目标旋转的角速度。该方法受单个特征点坐标的影响较小,可以提高求解的准确性。
记离散时域信号的采样序列长度为,采样周期为=1,则信号及其对应的频谱为:
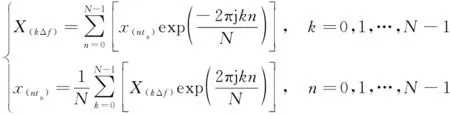
(3)
式中:频率的分辨率为Δ=;j为虚数单位。
视觉观测精度受到相机分辨率约束,并且部分跟踪识别的特征点轨迹在空间中的运动半径较小,可能引入较大的轨迹坐标观测误差,例如导致轨迹只有部分弧段或形状杂乱。在这类误差较大的特征点的||信号中难以提取出有效的频率信息,需要剔除。如图5所示,对于任选的两个特征点,特征点1的位置矢量的模变化幅度过小且没有明显的周期性变化,而特征点2虽然稳定跟踪时间较短,但其位置矢量的模表现出良好的周期特性,参考价值较高。为了提高目标角速度的求解精度,计算中剔除||变化幅度小于平均变化幅度的轨迹。

图5 特征点到左相机的距离Fig.5 Distance between the feature point and the left camera
采用FFT方法对特征点||变化幅度超过均值的各条特征点轨迹进行频谱分析。以第个特征点||信号的频谱分析为例,如图6,采用圆圈与三角标记出特征点||信号振幅||的极大值点,所对应的频率是信号中的主要频率。第个特征点||信号的频率与旋转失效卫星角速度之间满足=2π。记振幅||最大的频率为该特征点的有效频率(三角标记)。图6所示特征点轨迹的有效频率为0.059 Hz,对应目标角速度为0.371 rad/s。

图6 某一特征点位置矢量模的频谱特征Fig.6 Spectral characteristics of the module of position vector of a feature point
以3σ准则剔除角速度中的显著误差,并将其余角速度的均值作为失效卫星角速度的最终估计结果。如图7所示,在所给地面物理实验中,采用频谱分析获得了23个有效的角速度(星形标记),经过筛选共有14个可信度较高的角速度结果,它们的均值为=0.334 rad/s(实线),与失效卫星的真实角速度=0.370 rad/s(虚线)相比,角速度测量的绝对误差为0.036 rad/s,相对误差为9.55%。
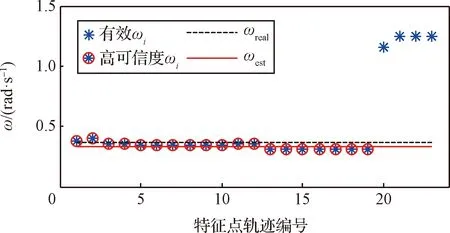
图7 地面物理实验目标角速度测量结果Fig.7 Target rotation angular velocity estimation under ground-based physical experiments
为了对比不同计算方法下,对失效卫星角速度求解的计算效率和精度,输入相同的特征点轨迹信息,分别使用本文设计的基于FFT的频谱分析方法、粒子群优化算法和圆周运动拟合的方法求解角速度,结果如表2所示。粒子群优化方法以轨迹上任意一点为起点,通过后续点与起点间距离的变化规律优化求解目标角速度,计算过程较为复杂,用时最长,通过10次求解结果可知,角速度的求解性能不稳定,可能达到很高精度,但也可能有较大误差。用圆周运动拟合的方式与本文所提FFT频域分析方法相对比,失效卫星角速度的求解精度相近,但圆周运动拟合方式计算用时较长,且精度与拟合算法参数设置有关,为达到较高的求解精度,需要针对不同算例调整算法参数。而FFT频域分析方法不需要额外参数调整,对旋转目标轨迹特性的分析具有一定的普适性,同时计算用时相对较少,整体求解性能最优。
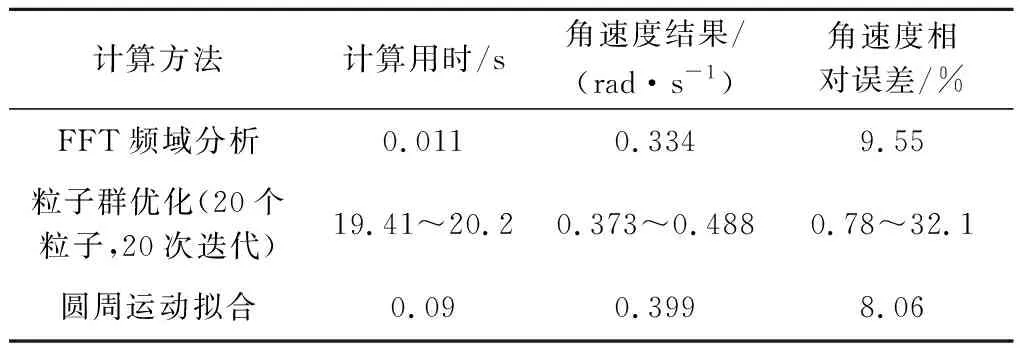
表2 目标运动周期检测方法性能对比Table 2 Performance comparison of target motion period detection methods
4 消旋接触方案设计
通过视觉测量获取消旋目标的几何构型与运动信息后,可以有针对性地选取要接触的区域并分析消旋需求,从而指导机械臂的运动规划和实施接触操作。本节依据稳定跟踪识别特征点的轨迹和失效卫星的运动状态,分析消旋目标上适宜接触的区域,给出双机械臂的接触构型,并在约束消旋操作时间的情况下分析接触强度需求。
对第2节所得的特征点点迹进行曲面拟合,得到失效卫星的运动包络,如图8所示。根据实验数据,本算例中,失效卫星旋转轴单位矢量在世界系的分量列阵为=[0.015 0.516 0.856]。在失效卫星旋转轴附近,运动包络曲面的曲率较小,并且附近存在大量能够长时间稳定跟踪识别的特征点,形成了最为密集的点迹,表明该区域在目标运动时保持空间朝向基本稳定,因此容易在该区域实现稳定接触,适宜选为接触区域。此外,识别到的特征点的全部点迹呈现出平缓微凸的运动包络,这表明当接触位置距离旋转轴较远时,机械臂仍然能够较为安全地抵近目标表面,碰撞风险较小。相反,当运动包络呈现凹的形态,则要求机械臂尽可能以贴近旋转轴的状态靠近目标,规避与目标的意外碰撞。
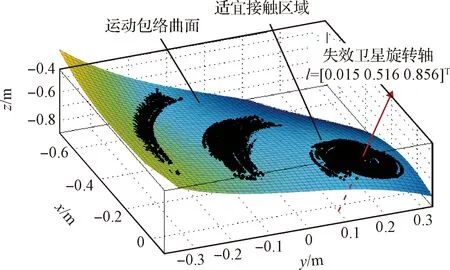
图8 旋转失效卫星运动包络曲面Fig.8 Motion envelope surface of the rotating failed satellite
依据双目立体视觉原理观测目标的几何外形,失效卫星主要由立方形中心体和两侧太阳帆板组成,中心体边长约0.18 m,两侧帆板的端部之间的距离约为1.09 m。目标表面适宜接触的区域沿旋转轴方向对称分布,如图9。为了在操作中更好地保持服务航天器的平衡,以及避免接触后推走漂浮的目标,设计采用双机械臂同步操作,从两侧对称地接触目标两侧的适宜接触区域。同时为减小机械臂与目标意外接触的风险,设计机械臂末端作动器的期望姿态平行于目标旋转轴,垂直接触目标。
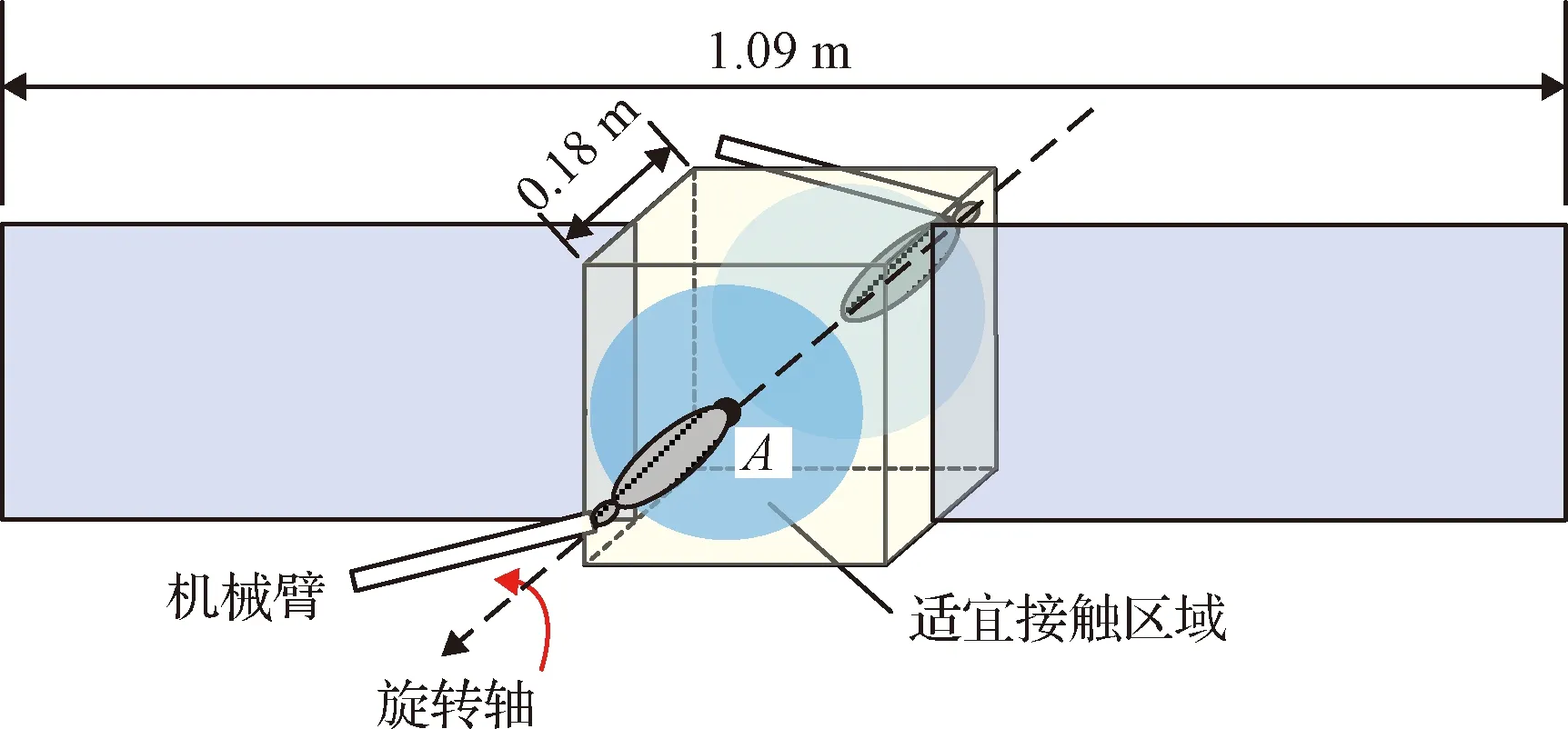
图9 双臂接触构型Fig.9 Configuration of the dual-arm robot during contact
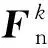
接触力矩在失效卫星旋转轴方向的投影为负,记该投影的模长为,是起到消旋作用的有效力矩。当给定最长消旋时间为,应有:

(4)
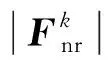

(5)
不同种类卫星的密度有所不同,卫星平台的平均密度约为150~300 kg/m,将所观测的失效卫星视为卫星平台,则目标质量约为4.2 kg,绕最大惯量轴的惯量约为=0.143 kg·m。在=20 s的情况下,双臂消旋力矩沿目标旋转轴方向投影的模应不小于0.0024 N·m。
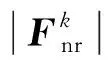
5 结 论
本文针对旋转失效卫星的接触式消旋任务,采用双目视觉测量,提出一种双重光流约束特征点迭代跟踪方法,获得了目标上稳定跟踪识别特征点的轨迹,并采用FFT方法进行轨迹频域分析,求解失效卫星的旋转角速度。在地面物理仿真中,目标旋转角速度求解的相对误差为9.55%,兼具求解准确性和快速性。结合对失效卫星的几何结构观测和运动包络拟合,给出了目标表面适宜接触区域和双机械臂的对称垂直接触构型。在约束接触消旋时间的条件下,给出了机械臂末端的力输出能力需求,可为消旋任务中机械臂操作和控制器设计提供参考。

