基于刚体自由转动的连续推力消旋方法研究

卿金瑜，武海雷，师 鹏，赵育善

(1. 北京航空航天大学 宇航学院，北京 100191；2. 上海航天控制技术研究所，上海 201109)

0 引言

随着航天事业的不断发展，人类每年都会向太空发射大量的航天器[1-4]，以满足各种航天任务的需要。与此同时，太空中因故障或寿命失效的航天器及长年积累的太空垃圾越来越多，对在轨航天器的安全运行构成了严重威胁。为解决这一问题，在轨主动移除(active debris removal)失效航天器和空间碎片已迫在眉睫。而主动移除技术的关键是实施在轨捕获，由于失效航天器在空间中可能存在转速过快的问题，这就给捕获带来了巨大挑战。若是能在捕获前对目标进行消旋处理，降低其转速，将有利于后续抓捕和回收。

国内外许多学者开展了与非合作目标在轨服务相关的研究[5-7]，但消旋技术尚处在发展阶段。按照消旋力矩是否与目标接触可将消旋分为接触式和非接触式两种方法。接触式方法主要有机械臂消旋和粘附式消旋，适用于较大目标的快速消旋，机械臂消旋是利用其末端执行器与非合作目标相接触而产生的力矩消旋，而粘附式消旋则是将纳米卫星直接附着在目标上，通过自带的发动机产生力矩消旋；非接触式消旋主要有气动消旋、静电消旋和电磁消旋等，由于无需与目标相接触，减小了碰撞的危险，可在安全距离外降低目标转速。文献[8]提出了利用减速刷消旋的方法，该方法适用于单轴自旋目标，但在实施消旋前需要服务航天器进行复杂绕飞。文献[9-10]提出了利用空间绳系机器人消旋的方法，该方法可在线辨识目标质量及惯性参数，能够快速稳定目标姿态，但在防止系绳缠绕方面还有待研究。文献[11]提出了利用库仑力静电消旋的方法，该方法可在安全距离外提供毫牛级的消旋力直至消旋完成，但不适合较大质量目标的消旋，另外在消旋过程中的充放电控制算法还有待研究。为此，本文提出一种简单、直接的附着式连续小推力消旋方法，在目标合适的位置附着纳米卫星，利用纳米卫星自带的动力装置对目标转速进行衰减。本文通过分步消旋的策略来研究空间目标的消旋，首先探讨了轴对称目标的消旋方法，然后在轴对称目标消旋方法的启发下，研究了更为普遍的一般目标消旋方法，得到了消旋步骤。最后通过仿真验证了消旋方法的有效性。

1 目标在空间中的运动

失效卫星或空间碎片在空间中自由运动，在摄动力、光压等的长期作用下最终将趋向于自由翻滚状态，绕其最大惯量主轴旋转。在本体坐标系下，通常可将其看作自由旋转的刚体，满足欧拉方程

(1)

式中：坐标系x，y，z为中心主轴坐标系；ωx，ωy，ωz为相对于惯性参考系的角速度在坐标系x，y，z上的分量；Jx，Jy，Jz分别为质点系对x，y，z轴的转动惯量。

2 目标的消旋

2.1 轴对称目标的消旋

消旋是通过对消旋目标施加适当的外力矩，衰减或停止目标转动的动作。设目标质量以本体坐标系的z轴为对称分布，关系为[12]

(2)

由式(2)可得

(3)

因此空间中轴对称目标的运动满足式(3)。通常情况下，消旋目标绕最大惯性主轴的旋转速度最快。从式(3)可看出，方程组的第3个方程独立于其他2个方程，因此考虑首先消除绕最大惯性主轴(z轴)方向的旋转速度。对z轴施加与角速度方向相反的力矩Mz，这时欧拉方程变为

(4)

由式(4)的第3式可得

(5)

通过给定初始值，由式(5)可求得使ωz减小到0所用的时间。

在消旋过程中ωz不恒为0，由式(4)前2式可得

(6)

则有

(7)

式(7)表明：在对最大惯量主轴进行消旋的过程中，绕x轴，y轴转动的总能量不变，始终为一常值，C1可由给定的初始角速度值求得。可以发现，先对最大惯量主轴进行消旋不会消耗发动机多余的燃料。因此，该消旋方法是一种较好的消旋方式。

当ωz衰减为0或小量时，停止施加Mz，式(3)变为

(8)

式(8)中不存在耦合关系，分别对x，y轴施加力矩Mx，My便可消旋，于是有

(9)

由式(9)可得

(10)

给定初始条件，由式(10)可得到对x，y轴消旋所用的时间，至此整个消旋过程完成。

2.2 一般目标的消旋

设Jz>Jy>Jx，受轴对称目标消旋方法的启发，同样考虑先对z轴施加控制力矩Mz，则式(1)可表示为

(11)

由式(11)前2式左右交叉相乘，整理可得

(12)

由于ωz不恒为0，则式(12)的解为

(13)

对式(13)积分，整理可得

(14)

式中：C2为与初始条件相关的常数。由式(14)可知，当只有Mz作用时，ωx和ωy满足椭圆约束关系。若Mz与ωz始终反向，Mz作负功，ωz变化的总趋势是减小的。

下面研究ωx，ωz的变化规律，由式(11)中第1，3式左右交叉相乘，整理可得

(15)

其中：Mzωz≤0。由式(15)可得两组解

(16)

ωy≡0

对式(16)第1组解两边积分，可得

(17)

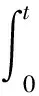
决定。P1为单调递增，当P1>0时，焦点位于ωx轴上，当P1<0时，焦点位于ωz轴上。

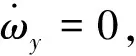
(18)

(19)

这时，消旋过程简化为：在z方向作用Mz直至ωz=0。

接着研究ωy、ωz的变化规律，由式(11)中第2，3两式左右交叉相乘，整理可得

(20)

可得到两组解

(21)

对式(21)中第1式两边积分，可得

(22)

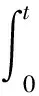
决定。P2为单调递减，椭圆越来越小，ωy和ωz同时趋于0，结合式(17)可知，此时ωx趋于一固定值，且该值的大小与式(22)所表示椭圆的1/2长轴值相等。当ωy和ωz趋于0时，停止作用Mz，在x方向作用Mx，直至ωx趋于0，完成整个消旋过程。

(23)

(24)

这时，消旋过程同样简化为，在z方向作用Mz直至ωz=0。

3 仿真

轴对称目标的消旋过程较为简单，这里不再给出仿真算例。假设空间中有1颗失效卫星，已知该星的主转动惯量Jx=9.2 kg·m2，Jy=11.7 kg·m2，Jz=18.2 kg·m2，则经过观测，测得卫星的初始角速度为ωx=2.1 rad/s，ωy=-3.4 rad/s，ωz=5.7 rad/s。

对z方向施加控制力矩

Mz=-0.2sign(ωz)N·m

然后当ωy和ωz趋于0时，撤销z方向的控制力矩，同时对x方向施加控制力矩

Mx=-0.2sign(ωx)N·m

当ωx=0时，消旋完成。

第1步，对z轴施加控制力矩

Mz=-0.2sign(ωz)N·m

仿真时间700 s，消旋过程如图1所示。

图1显示了失效卫星旋转速率整体变化趋势，图1中a为消旋过程的局部放大图，图中ωy和ωz之间的类椭圆约束关系清晰可见，与2.2节推导的方程相符。图2～4分别显示了单个方向上角速度的变化规律，随着时间的变化，各个方向上的角速度都达到了预想状态。大约在683 s时，ωz减小到0附近，ωy减小到13.57 mrad/s附近，ωx趋于一固定值，该值的大小与式(22)所表示的椭圆的其中一个半长轴值相等。ωy未趋于0是由于施加的外力矩值过大造成，考虑实际情况，13.57 mrad/s的转速已能满足工程实践需要，这里不在进一步对ωy进行消旋处理。

图1 旋转速率整体变化趋势Fig.1 Changing trend of rotation rate

图2 ωx旋转速率响应Fig.2 Rotation rate response of ωx

图3 ωy旋转速率响应Fig.3 Rotation rate response of ωy

图4 ωz旋转速率响应Fig.4 Rotation rate response of ωz

第2步，在683 s时，停止作用Mz，同时对x轴施加控制力矩Mx=-0.2sign(ωx)N，仿真时间200 s，消旋过程如图5、6所示。图5为失效卫星整体旋转速率变化趋势，图6为各分量随时间变化过程图，两幅图中可以清楚看到ωx不断减小，ωy和ωz也在很小的范围内变化，大约在176 s，ωx减小到0附近，此时停止施加外力矩，消旋完成。

图5 旋转速率整体变化趋势Fig.5 Changing trend of rotation rate

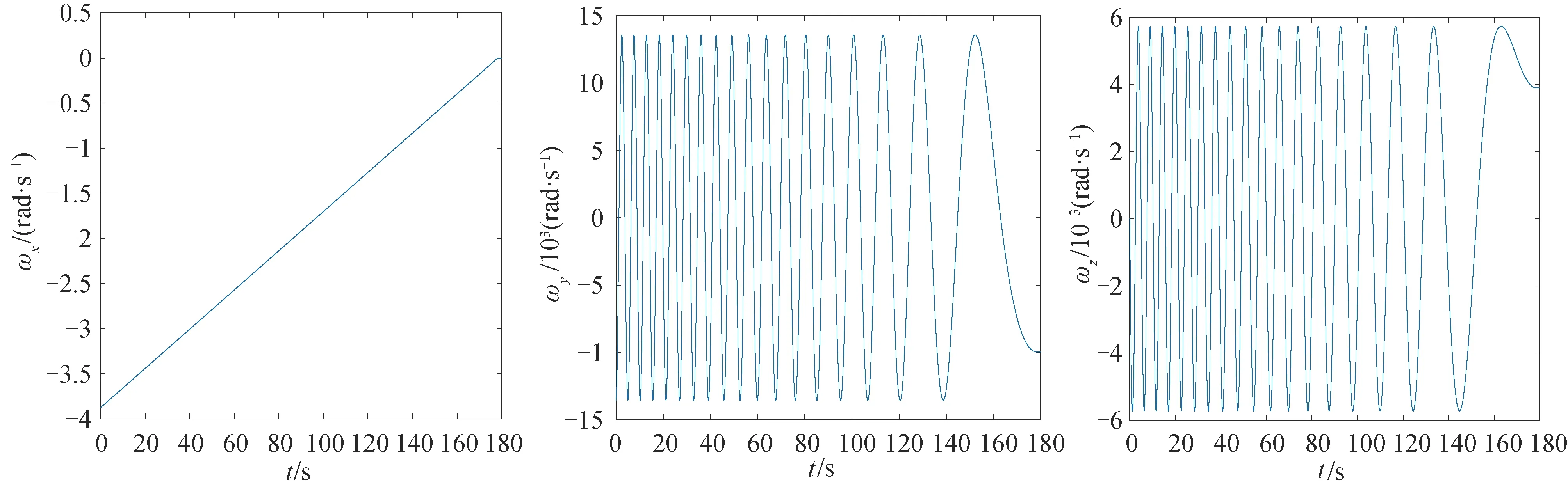
图6 各分量响应Fig.6 Response of each component

4 结束语

本文针对空间中失效卫星或空间碎片的消旋问题，探讨了轴对称目标和一般目标的消旋过程，得到了消旋步骤。通过给定的消旋顺序和方向作用控制力矩，消旋目标能有效降低旋转速度，实现消旋目的。通过仿真算例对该方法的可行性进行了校验，校验结果与预期一致。相较于其他消旋方法，该方法更为简单直接，且对控制系统的要求较低，更易实现。研究对惯性参数识别技术依赖较大，目前精度较高的识别方法主要还是接触式识别，但有的目标难以直接接触，因此后续可在非接触式目标惯性参数估计方面展开研究。

[1] ANDREW M L, RICHARDS M G, HASTINGS D E. On-orbit servicing: a new value propositionfor satellite design andoperation [J]. Journal of Spacecraft and Rockets,2007, 44(4): 23-28.

[2] 张森, 石军, 王九龙. 卫星在轨失效统计分析[J]. 航天器工程, 2010, 19(4): 41-46.

[3] 李岩, 党常平. 空间在轨服务技术进展[J]. 兵工自动化, 2012, 31(5): 79-82，86.

[4] 闫海平, 和宇硕, 冯月, 等. 失效卫星再利用系统方案设想[J]. 航天器工程, 2014, 23(5): 12-17.

[5] 崔乃刚, 王平, 郭继峰, 等. 空间在轨服务技术发展综述[J]. 宇航学报, 2007, 28(4): 805-811.

[6] STAMM S, MOTAGHEDI P. Orbital express capture system:concept to reality[C]// Spacecraft Platforms and Infrastructure,Albuquerque: SPIE, 2004: 78-91.

[7] 曹喜滨, 李峰, 张锦绣, 等. 空间碎片天基主动清除技术发展现状及趋势[J]. 国防科技大学学报, 2015, 37(4): 117-120.

[8] NISHIDA S I, KAWAMOTO S. Strategy for capturing of a tumbling space debris [J]. Acta Astronautica, 2011, 68(1): 113-120.

[9] WANG D, HUANG P, MENG Z. Coordinated stabilization of tumbling targets using tethered space manipulators [J]. IEEE Transactions on Aerospace and Electronic Systems, 2015, 51(3): 2420-2432.

[10] HUANG P, ZHANG F, MENG Z, et al. Adaptive control for space debris removal with uncertain kinematics, dynamics and states [J]. Acta Astronautica, 2016, 128: 416-430.

[11] BENNETT T, SCHAUB H. Touchless electrostatic three-dimensional detumbling of large axi-symmetric debris [J]. The Journal of the Astronautical Sciences, 2015, 62(3): 233-253.

[12] 赵育善, 师鹏. 航天器飞行动力学建模理论与方法[M]. 北京:北京航空航天大学出版社, 2012: 44-48.