薄板光学反射面面形变形驱动器集成设计

孙小庆，王智磊，杨斌堂，夏 昂，赵发刚

(1. 上海交通大学 机械系统与振动国家重点实验室，上海 200240； 2. 上海卫星工程研究所，上海 200240)

0 引言

为了提高光学载荷的集光、分辨能力，光学载荷成像系统的口径变得越来越大，如MOIRE卫星的口径达到了20 m[1-2]。随着口径的增大，空间特殊环境所带来的负面影响越来越明显，于是主动光学技术应运而生。主动光学技术实质上是通过实时控制镜面周围驱动器的输出来调整面形精度的[3]。目前，电机式、液压式等传统驱动方式已在大型地面天文望远镜中得到了应用[4-5]。如：李国平等[6]利用步进电机驱动减速器、精密丝杆型式及高精度的杠杆缩放机构，实现了高精度、大行程的微位移驱动器；张丽敏等[5]设计了由步进电机驱动谐波减速器、带动丝杠传动组成的驱动器，该驱动器行程达10 mm。尽管采用此类传统驱动方式能实现较大行程，兼具一定精度，但由于此类驱动器体积、质量较大，以及附加传动部件存在间隙等因素，限制了其在空间领域的进一步应用。因此，以压电陶瓷、GMM (巨磁致伸缩材料)等智能材料为作动机理的新型微精密驱动技术得到了重视。针对不同需求研制不同行程的新型驱动系统也成为了当前主动光学领域研究和应用的热点。如:YUAN等[7]针对光学跟踪镜设计了以压电陶瓷为主动作动的驱动系统，该系统能够实现较大的偏转角度；JING等[8]在压电陶瓷驱动器的基础上设计了2轴光学扫描机构，实现了光学镜面约50 mrad的偏转。压电陶瓷驱动器工作电压通常为几十甚至上百伏，且价格昂贵，为航天领域的应用带来了一定负担[9]；SUN等[10]针对航天微振动控制设计了以磁致伸缩材料为作动、结合放大机构的驱动平台，行程已近毫米级，通过对驱动器进行了闭合导磁回路磁轭设计，有效避免了漏磁对外界的影响；ZHANG等[11]对磁致伸缩驱动器进行了集成化设计，实现了在0～130 Hz内140 μm的位移稳定输出。整体来看，压电陶瓷驱动结构简单、整体尺寸相对较小，通过电压直接驱动材料自身产生形变、无中间能量转换环节，减小了因传递、转换过程中的能量损耗。而磁致伸缩驱动需要通过励磁线圈产生磁场，进而驱动材料自身产生形变，在此过程中能量存在一定损耗。磁致伸缩驱动相比压电驱动驱动效率较高，而且可以在低电压下驱动，这样就减轻了压电陶瓷驱动需配置变压器等设备的负担。另外，磁致伸缩驱动的低频性能更好，输出力也更大，更适合空间环境下对光学形面的主动面形调整。

本文在结合某光学载荷薄板反射面形面变形控制的基础上，提出了一种基于GMM的微位移精密驱动系统。研究了大型柔性太阳翼扰动对敏感载荷的影响，给出了驱动器的整体结构设计，通过采用闭合磁路设计，减小了漏磁对空间其它器件的影响，优化了柔性位移放大机构，建立了驱动器动力学模型，并采用模糊自适应PID控制对驱动系统进行闭环控制仿真。

1 影响因素及分析

光学载荷入轨后，微重力环境、空间辐射、热振动、微振动等因素会引起光学载荷形面的变形，进而降低光学系统成像质量[12]。大型柔性太阳翼因冷热交变产生的热致微振动所带来的光学形面的周期性变形作为关键干扰因素尤其需要引起重视。考虑到该载体航天器结构的复杂性，进行详细的理论建模具有相当难度。因此，在地面相关实验数据的支撑下利用有限元仿真软件ANSYS对其进行了合理简化。简化时，注意保留舱体主骨架的完整从而确保微振动传递路径的完整，主骨架为蜂窝夹心结构，可以利用shell63单元进行模拟；其次，对于较大的舱内载荷，通过mass21节点单元的方式进行等效，并通过刚性约束建立节点与舱体臂对应节点的耦合。载荷根据文献[13]中对太阳翼进出地影产生的热颤振分析，可等效为如下干扰力矩模型

(1)

式中：d为热颤振的绕动力矩；Ai为颤振扰动幅值；pi为第i阶颤振频率；φi为初相位，可当作[0，2π]内均匀分布的随机变量。

依据前期实验对太阳翼关键工况下热颤振载荷数据的统计分析，结合有限元仿真技术进行结构瞬态动力学研究，得到光学形面处的振动响应，并对6个自由度的振动响应进行后处理分析。图1为沿x方向的振动响应结果，不难看出，太阳翼热颤振将会引起光学形面位置处沿x方向的振幅，振幅约为1.5×10-4mm，频率为0.08 Hz。

图1 沿x方向振动响应Fig.1 Vibration response along x axis

表1为6个自由度方向上的振动响应结果。由表1可得：热颤振将主要影响y轴与z轴方向上的振动响应，产生的线位移为0.25 mm，同时最大角位移为3.5×10-5rad。由于光学形面精度要求较高，该量级的干扰必须进行主动补偿。

表1 光学形面处振动响应结果统计

2 巨磁致伸缩驱动器集成设计

2.1 巨磁致伸缩驱动原理及整体集成设计

GMM为在室温和低磁场下能产生很大磁致应变的稀土金属化合物，其形状和长度会随外界磁场变化而改变，典型材料为Terfenol-D，成分为TbDyFe。巨磁致伸缩驱动就是利用GMM具有的磁致伸缩效应，来实现微精密作动的一项技术。通常利用励磁线圈对磁致伸缩棒施加磁场，通过控制电流大小改变磁场强度，磁致伸缩驱动器产生预期的位移或力。根据对面形影响因素的分析，本文以最大输出位移为设计指标[14]，提出了磁致伸缩驱动器的总体结构示意图，如图2所示。

图2 磁致伸缩驱动器整体方案及驱动器剖视图Fig.2 Overall scheme and section view of magnetostrictive actuator

由图可见：本文提出的整体方案主要由磁致伸缩驱动器、柔性位移放大机构以及柔性铰链组成。其中，磁致伸缩驱动器主要由输出杆、预紧螺母、直线轴承、Terfenol-D棒、励磁线圈、内磁轭、导磁端盖、外磁轭、套筒、导磁柱、预紧碟簧组成。考虑到低轨卫星有效载荷对空间磁场相当敏感，需对磁致伸缩驱动器进行磁屏蔽。所以，磁致伸缩驱动器采用了闭合磁路设计，闭合磁路由内磁轭、外磁轭、导磁圆柱、导磁端盖、磁致伸缩棒组成。线圈通电后，磁感线将通过内外磁轭以及导磁圆柱、导磁端盖组成闭合磁路，既为磁致伸缩棒提供稳定的磁回路，又能有效降低漏磁。由于Terfenol-D棒只在一定偏置磁场和预应力下才能达到较好输出效果，为简化设计，偏置磁场采用了给螺线管提供持续恒定电流的方式来实现，并通过控制电流来实现磁场强度的精确控制。预应力的施加主要通过输出杆、预紧碟簧及预紧螺母组成的预压组件实现，通过调节预紧螺母的旋转角度来设定最佳预应力。

在工作时，设定最佳偏置磁场(向线圈输入直流电流I1)和预应力，此时磁致伸缩棒伸长，再向线圈输入幅值为I2的交流电流，总电流为I1±I2，在该交变磁场作用下，磁致伸缩棒将在Δl位置处做周期性上下往复运动。由于线圈与磁轭的设计已有较成熟的理论，本文根据驱动系统能量损耗最小的设计原则，综合得到磁致伸缩驱动器的关键参数，见表2。

2.2 柔性放大机构优化

由于所设计的驱动器难以弥补面形受扰时较大的变形，因此本文提出了利用柔性位移放大机构与磁致伸缩驱动器结合驱动的方案。柔性放大机构(见图3)既要考虑其应实现所需的放大比，又需考虑柔性环节强度、柔性放大机构整体固有频率等因素。为使柔性机构具有较强的抵抗外部负载的能力、较小的转动刚度，将目标函数[15]设为

(2)

约束条件为

(3)

表3 柔性位移放大机构参数

图3 柔性位移放大机构Fig.3 Flexure hinged displacement amplifier

3 巨磁致伸缩驱动器性能仿真

3.1 磁致伸缩驱动器动力学建模

本文设计的巨磁致伸缩驱动器等效动力学模型如图4所示。图中：Kr，Cr，Mr，Kl，Cl，Ml，u，F，F′分别为Terfenol-D棒的等效刚度系数、等效阻尼系数、等效质量、预载弹簧的刚度、阻尼、预载弹簧与输出杆的质量、磁致伸缩驱动器的输出位移、GMM棒的输出力、输出端受到的外部作用力。

图4 巨磁致伸缩驱动器等效动力学模型Fig.4 Equivalent dynamic model of actuator

磁致伸缩材料的线性压磁方程[16-17]为

ε=σ/Er+dH

(4)

式中：ε为GMM棒的轴向应变；σ为GMM棒的轴向应力；Er为GMM棒的弹性模量。

B=d′σ+μMH

(5)

式中：d′为磁致伸缩轴向压磁系数；B为GMM棒截面的磁通量密度；μM为GMM棒的相对磁导率；H为GMM棒所处的平均磁场强度，工程应用中通常可表示为[18]

(6)

式中：N为线圈匝数；δ为磁回路系数，根据所设计的驱动器形状，可取2；lr为GMM棒的长度。

由于ε=u/lr，σ=-F/Ar，则驱动器输出位移可表示为

u=uσ+ua=-F/Kr+d′Hlr

(7)

若考虑Terfenol-D棒的质量与阻尼，则式(7)可改为

(8)

在驱动器输出端，根据牛顿第二定律，得

(9)

联立式(8)、(9)得磁致伸缩驱动器的整体动力学方程，为

(10)

式中：Me为等效载荷,Me=Mr+Ml；Ce为磁致伸缩驱动器的等效阻尼,Ce=Cr+Cl；Ke为磁致伸缩驱动器的等效刚度,Ke=Kr+Kl；u′为驱动器的位移输出。设计的柔性放大机构的固有频率远大于磁致伸缩驱动器正常工作的输出频率，根据优化结果，可视柔性放大机构能稳定输出4倍于驱动器输出的位移。

联立式(6)、(10)进行拉氏变换，得到驱动器的输出位移和输入电流间的传递函数，为

(11)

根据该驱动器输出位移与输入电流间的传递函数，利用MATLAB对驱动器性能进行仿真。所设计的驱动器相关参数为：Me=1.15 kg，K=31.8 kN/m，C=5.15 kN·s/m，Kr=30 MN/m，N=1 000匝。绘制驱动器的理论传递函数伯德图(见图5)，可得驱动器固有频率约为800 Hz，这将保证驱动器在中低频形面补偿时具有稳定的输出，避免自身共振的影响。

图5 理论传递函数伯德图Fig.5 Bode diagram of transfer function

3.2 磁致伸缩驱动器驱动及隔振性能仿真

3.2.1 模糊自适应PID算法

针对所设计的新型驱动器，控制策略的选择对最终输出性能有很大影响。本文考虑采用模糊自适应PID控制，其控制原理如图6所示。图中：e为系统误差，e=yd-y；yd为最佳期望值(desired value)。

图6 模糊自适应PID控制原理图Fig.6 Control block diagram of fuzzy adaptive PID algorithm

该系统包含1个双输入三输出的模糊控制器，利用模糊控制对PID控制器进行三参数实时非线性调整，系统能达到较好的动态与静态性能[19]。若kp0，ki0，kd0为初始参数，则利用该控制算法得到的模糊PID参数为

(12)

表4 kp的模糊控制规则表

3.3.2 性能仿真

为进一步验证驱动器的闭环性能，利用动力学模型搭建SIMULINK仿真框图，并利用模糊自适应PID算法进行闭环定位控制。驱动器期望幅值为250 μm、频率为1 Hz，正弦输出跟踪情况如图8所示。由图可见：该驱动器能很好实现期望的位移，最大误差小于1 μm。

图7 模糊推理输出曲面Fig.7 Fuzzy inference output surface

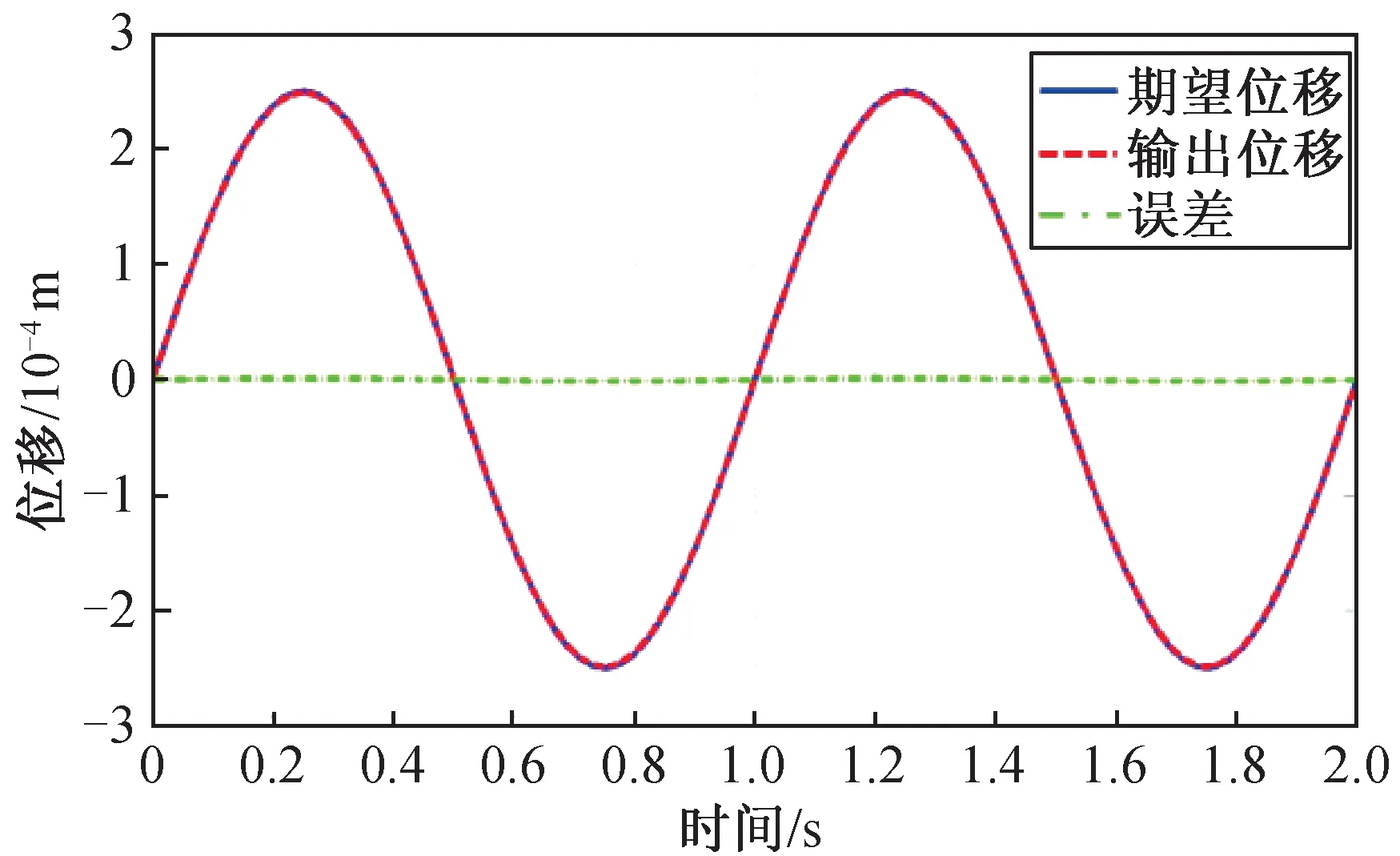
图8 驱动器正弦输出响应Fig.8 Sinusoidal output response

图9为驱动器三角波输出响应。由图可见，通过闭环控制实现对三角波的精密跟踪，最大误差同样小于1 μm。结果表明：通过模糊自适应PID控制，设计的驱动器能达到预期的输出位移，并且保持了较高的定位精度。

图9 驱动器三角波输出响应Fig.9 Triangle wave output response

针对空间环境下持续存在的微振动影响，设计的驱动器还可用来对微振动进行主动控制。考虑航天器产生的微振动分别以典型的谐波扰动和随机扰动传递至驱动器底端，同样利用该控制算法进行隔振仿真。由于中、高频谐波扰动主要来自于控制力矩陀螺等高速运转部件工作产生的振动，因此将干扰以多谐波复合形式施加于航天器系统，经驱动器主动控制后，结果如图10所示，干扰位移从160 μm衰减到20 μm，实现了87.5% (-18.1 dB)的隔振效果。图11为驱动器对均方根值为18 μm的随机扰动的隔振作用，经主动隔振后干扰位移均方根值减小到51 μm，实现了72% (-11.1 dB)的隔振效果，表明设计的驱动器具有一定的隔振效果。结合上述仿真结果，本文所提出的磁致伸缩驱动方案能较好实现对较大位移的精密输出和控制，所设计的驱动器不仅可用来进行面型变形补偿，还可用来进行微振动主动控制。

图10 谐波干扰下的隔振效果图Fig.10 Vibration isolation effect under harmonic disturbance

图11 随机干扰下的隔振效果Fig.11 Vibration isolation effect under random disturbance

4 结束语

本文对薄板光学形面变形驱动器进行了系统性的分析与设计，利用有限元仿真分析了大型柔性太阳翼对敏感载荷的影响。提出了以磁致伸缩驱动和柔性放大机构联合作动的驱动系统方案。对磁致伸缩驱动进行了闭合磁路设计，有效减少了漏磁；对柔性放大机构优化，得到了关键结构参数。建立了驱动器动力学模型，并基于模糊自适应PID算法进行闭环控制仿真，开展了微振动主动控制研究，结果表明：设计的驱动器能实现幅值为250 μm、频率为1 Hz的输出跟踪，最大误差小于1 μm；对多谐波复合干扰实现了87.5% (-18.1 dB)隔振效果，对随机扰动实现了72% (-11.1 dB)隔振效果。本文设计的磁致伸缩驱动与传统压电类驱动相比，具有更长的输出行程、更高的输出精度，并具有一定的微振动隔振能力。由于磁致伸缩材料本身具有磁滞效应，隔振效果仍有提升空间，今后将从机构设计和控制的角度进一步提升系统的隔振能力。另外，考虑到航天工程应用对电磁环境的苛刻性以及系统结构尺寸的限制，本文的方案还有进一步优化与集成设计的空间，如磁致伸缩驱动磁轭结构的厚度、形状优化，以及散热设计等问题，亟待下一阶段进行解决。

[1] 张月. 打破传统光学系统设计概念的首个折叠式空间望远镜[J].航天返回与遥感， 2013(6): 98.

[2] 刘韬.美国向“弹性和分散”军事空间体系转型探析[J].科技导报， 2014, 32(21): 76-83.

[3] 张玉方, 李国平. 用于薄镜面主动光学的音圈力促动器设计[J].光学精密工程， 2013, 21(11): 2836-2843.

[4] 咸奎成, 彭福军. 大尺寸空间薄膜结构形状控制研究[J].噪声与振动控制， 2009, 29(6): 97-104.

[5] 张丽敏, 张斌, 杨飞， 等.主动光学系统力促动器的设计和测试[J]. 光学精密工程， 2012, 20(1): 38-44.

[6] 李国平, 苗新利. 一种微位移促动器的设计和检测[J].光学精密工程， 2005, 13(3): 332-338.

[7] YUAN G, WANG D H, LI S D. Single piezoelec-tric ceramic stack actuator based fast steering mirror with fixed rotation axis and large excursion angle [J]. Sensors and Actuators: A，2015, 235: 292-299.

[8] JING Z J, XU M L, FENG B.Modeling and optimization of a novel two-axis mirror-scanning mechanism driven by piezoelectric actuators [J]. Smart Mater. Struct, 2015, 24(025002): 1-12.

[9] 邵亮, 杨德华, 陈昆新， 等. 光学天文望远镜用微位移驱动器机构研究综述[J]. 天文学进展， 2009, 27(1): 70-79.

[10] SUN X Q, YANG B T, ZHAO L,et al. Optimal design and experimental analyses of a new micro-vibration control payload-platform[J].Journal of Sound and Vibration, 2016, 374: 43-60.

[11] ZHANG H, ZHANG T L, JIANG C B. Magnetostrictive actuators with large displacement and fast response [J].Smart Mater. Struct, 2012, 21(055014): 1-7.

[12] 鲁锷, 颜昌翔, 吴清文， 等. 空间光学遥感器环境适应性设计与试验研究[J].中国光学与应用光学， 2009, 2(5): 364-376.

[13] WIE B, LIU Q. Classical and robust H∞ control redesign for the Hubble space telescope [J]. Journal of Guidance,Control,and Dynamics, 1993, 6(16): 1069-1077.

[14] 赵龙. 基于超磁致伸缩驱动微振动主动隔振平台的设计研究[D]. 上海：上海交通大学， 2014.

[15] SUN X Q, YANG B T.A new methodology for developing flexure-hinged displacement amplifiers with micro-vibration suppression for a giant magnetostrictive micro drive system [J]. Sensors and Actuators A: Physical, 2017, 263: 30-43.

[16] 顾仲权， 朱金才， 彭福军, 等. 磁致伸缩材料作动器在振动主动控制中的应用研究[J]. 振动工程学报， 1998， 11 (4)： 381-388.

[17] CLARK A E. Magnetostrictive rare earth-Fe2compounds, ferromagnetic materials[M]. Holland：North-Holland Pub, 1980.

[18] BRAGHIN F, CINQUEMANI S, RESTA F. A model of magnetostrictive actuators for active vibration control [J]. Sensors and Actuators A: Physical, 2011(165): 342-350.

[19] 高常春, 张孟伟. 车载光电设备主动隔振平台支撑结构设计及模糊PID控制[J]. 机械设计与制造, 2012(3)： 179-181.