卫星集群网络仿真建模与路由算法性能分析
陈 庆,张锦绣,韩 飞
(哈尔滨工业大学 卫星技术研究所,黑龙江省 哈尔滨 150001)
0 引言
空间信息网络是一类以多种空间平台(平流层气球、卫星等)为载体,实时获取、传输并处理空间信息的综合性网络系统,具有独特的空间位置优势与社会发展需求[1]。卫星集群网络可承担空间信息网络骨干节点功能,其设计理念是围绕多颗卫星智能化协同工作展开,使其能承载更加复杂多变的空间任务[2]。卫星集群具有空间结构灵活、数据共享、工作协同、服务智能等特点,其相关技术研究既可为空间信息网络中卫星平台的建设提供技术借鉴,又可开拓新的卫星任务工作体系,构建以小型化卫星网络为主体的低成本且高效的卫星协同工作模式。
目前,卫星集群研究正处于初始阶段,在仿真验证与评估技术、网络协议设计与优化技术、多星协同控制技术、自适应任务决策技术等方面面临着诸多难题[2]。当前卫星集群的网络仿真平台普遍采用基于网络仿真软件NS-2和OPNET的卫星星座设计模式[3-4],但卫星集群网络的拓扑不同于卫星星座,其网络服务需求与卫星星座存在很大区别[2],因此现有仿真平台难以满足卫星集群网络仿真的需求。同时,卫星集群网络相关技术的研究主要集中于网络拓扑控制算法、网络容量研究、任务资源调度等[5-7],尚未有针对卫星集群网络路由协议的文献研究。
本文从仿真验证与评估技术角度出发,基于网络仿真软件NS-3和卫星场景分析软件STK搭建一个多功能的卫星集群网络仿真平台,并对典型的移动自组网路由协议进行仿真,分析卫星集群网络路由协议设计与优化的思路。
1 卫星集群网络与路由算法
1.1 卫星集群网络
作为空间信息网络天基平台的发展方向之一,基于星间链路协同工作的卫星集群技术已被广泛关注。由于侧重点不同,学术界对卫星集群的定义存在差异,但普遍将其同卫星星座和卫星编队飞行的概念区分。为方便后续讨论,结合文献[8-9]将卫星集群定义如下:在一定范围内相伴飞行,可协同工作的,能承载多类空间任务的多颗卫星构成的系统。卫星集群是对卫星编队的功能扩展,集群内各卫星除编队任务工作需求外没有严格的相对运动构型要求。另外,单个卫星集群也可作为一个“卫星个体”参与到卫星星座的构建中。
卫星集群网络示意如图1所示,包括群内网络和群间网络。其中:群内网络为单个卫星集群内基于星间链路(如射频链路、光链路等)构成的信息交互网络,集群内卫星由于部分空间任务协同工作需求需要进行信息交互、资源共享;群间网络为多个卫星集群基于星间链路组成的更大时空跨度的协同工作网络。

图1 卫星集群网络示意图Fig.1 Schematic diagram of satellite cluster network
集群内各卫星在一定范围内相互绕飞,其通信网络拓扑相较于卫星编队和卫星星座具有明显的动态变化特性,且网络内部数据交互更频繁。因此,本文主要针对卫星集群群内网络的路由性能进行分析。
1.2 典型的移动自组织网络路由算法
由于无人机集群网络、移动传感器网络[10-13]的拓扑结构特征与集群卫星网络相似,因此将其中3种典型的移动自组织网络(mobile ad-hoc network, MANET)路由协议应用到卫星集群网络中,并检验其网络性能变化。
1) 链路状态优化路由协议 (optimized link state routing protocol, OLSR)。该协议为一类表驱动路由算法,通过“Hello”和拓扑控制消息感知链路状态,并将这类状态信息传输到网络中所有节点。网络中单个节点利用网络链路拓扑信息,并结合最短路径算法计算下一跳路由节点信息。
2) 目标序列距离矢量路由 (destination-sequenced distance vector routing,DSDV)。该协议为一类表驱动路由算法,网络中任一节点更新并维护着自身到达各个目的节点的路由信息,降低了传输路径构建过程中的时延,但同时由于路由表周期性更新,增加了各节点的能量和带宽消耗。
3) 自组网按需距离矢量路由(ad-hoc on-demand distance vector routing,AODV)。该协议为一类按需路由算法,其在源节点需要发送数据且没有存储到目的节点的有效路由时,才在网络中发起路由查找过程,找到合适的传输路径。
2 卫星集群网络仿真平台
卫星集群网络仿真平台主要面向单个卫星集群网络和多个卫星集群构建的综合网络,可验证路由算法、拓扑控制算法、任务调度协同策略等卫星集群网络相关技术的应用性能。目前,主流的开源网络仿真软件为NS-2,OMNET++,NS-3等。本文选用三维运动模块扩展性更好的NS-3作为卫星集群网络仿真环境搭建的基础,并结合商用卫星仿真软件STK用于卫星场景显示,实现仿真平台搭建。该仿真模型同当前主流基于NS-2的卫星集群网络仿真模型相比,能准确模拟多星相互绕飞运动,且其组网通信协议具有更好的扩展性与通用性,从而有助于卫星集群网络的数据传输性能全面,分析准确。
卫星集群网络仿真平台主要由卫星运动模块、STK显示部分和卫星集群生成模块构成,如图2所示。图中:卫星运动模块负责提供仿真中卫星位置和速度的数据;STK显示部分主要通过导入仿真中生成的各卫星的运动轨迹数据对卫星集群的仿真场景进行三维显示;卫星集群生成模块负责依据给定参数随机生成符合要求的卫星集群网络。
2.1 卫星运动模块与STK显示
卫星运动模块是用来模拟卫星集群中的各个卫星节点在仿真过程中的位置和速度变化。卫星运动模块功能划分如图3所示。图中,在NS-3软件的标准移动模块(Mobility model)的基础上,加入具有卫星特性的参数预处理模块、轨道机动模块、轨道动力学模块。


(1)
式中:μ为地球引力常数;r为卫星的地心距;Re为地球平均半径;J2和J3为摄动系数。
考虑到卫星集群一般位于较低轨道,易受大气阻力的影响,因此在式(1)的基础上还加入了大气阻力模型。大气阻力产生的卫星加速度变化量为
(2)
式中:CD为阻尼系数;A为卫星的迎风面积;m为卫星质量;ρ为卫星所处位置的大气密度;vr为卫星速度;ev为卫星的速度方向矢量。
本文结合式(1)和式(2),基于NS-3软件内部的Mobility model模块,搭建了适用于NS-3仿真的卫星运动模型,使由Node container类定义的移动节点均可配置该模型。该卫星运动模型仅适用于卫星集群群内和群间网络,而且适用于行星际通信网络、空间信息网络等以卫星为运动节点的通信网络[14]。
为直观观察仿真过程中卫星的运动情况,仿真平台还支持实时仿真模式。该模式基于NS-3内部的实时仿真模块和STK的Connect接口,通过配置NS-3的Simulator implementation type属性,在仿真过程中将各颗卫星的位置和速度数据以TCP/IP socket的形式发送给STK,从而驱动STK显示窗口的卫星集群实时运动。
2.2 卫星集群生成模块
卫星集群生成模块依据双星编队飞行动力学模型,在给定的卫星构建相对运动坐标系以及给定的卫星集群范围R随机生成指定数量的卫星。本仿真平台中采用的卫星相对运动模型为忽略各项摄动力作用的HILL方程,其公式为
(3)
式中:n为参考卫星的瞬时间角速度。依据式(3)可得卫星相对运动位置和速度随时间的变化关系,仿真平台采用分区枚举的方法,筛选出在给定范围内的卫星参数(相对位置和速度),在一定时间内使卫星相对位置满足x2+y2+z2≤R2。通过坐标系转换,将所生成的各卫星参数转化为地心惯性系下的数据,导入卫星运动模块,作为各卫星运动的初始参量。
2.3 仿真流程
基于NS-3的非实时模式下的卫星集群网络仿真流程包括以下步骤。
1) 卫星集群仿真节点初始化。利用NS-3软件中的Node container类定义了指定数目的卫星节点,将参考卫星的平均轨道要素及卫星运动模型配置到卫星节点对象中。再结合卫星集群生成模块随机生成仿真所需的其余卫星的初始位置与速度数据。
2) 网络仿真环境配置。将各颗卫星的通信协议模型配置为MANET中常用的TCP/IP和Ad-hoc (IEEE 802.11)框架,并将星间传输模型设置为适用于自由空间通信的Friis传输模型,忽略宇宙背景辐射的影响,并配置卫星的发射功率为30 dBm,接收灵敏度为-90 dBm,传输速率为2 Mbit/s。
3) 星间任务数据生成模型定义。配置仿真所需的任务数据。任务数据采用UDP的数据传输模式,默认数据包大小为512 B,依据卫星集群不同的工作状态,制定了2类数据生成模式:一是当卫星处于协同控制模式时的少量数据交互(低延时、低误码率);二是当卫星处于任务数据回传模式时的大量数据交互,如卫星完成对地观测任务后将图像数据传输到它星进行处理并传回地面的过程。
4) 卫星集群网络性能分析。结合NS-3软件内部的流监测模块(Flow monitor)、时延统计模块(Delay-jitter-estimation)等网络性能分析模块,将卫星集群网络仿真过程中的各项关键数据保存到不同CSV文件,以对路由算法的各项性能进行进一步分析与研究。
3 性能仿真与分析
3.1 性能指标与仿真场景
仿真实验采用了3种性能评价指标。
1) 端到端平均延时。数据报文在发送卫星和接收卫星IP层之间传输所耗费的平均时间。该指标直接影响卫星集群协同工作性能,平均延时过大会导致姿态协同等控制算法精度降低,同时延长任务有效数据的传输时间,增大数据丢包的概率。
2) 分组交付率。卫星在一定时间内接收的数据报文数目和发送数目之间的比值。该指标反映了网络传输的稳定性,较低的分组交付率表明大部分数据在传输过程中未能正常到达接收卫星,严重影响多星协同工作的性能,甚至导致整个卫星集群网络无法正常工作。
3) 归一化路由开销。卫星网络中发送的路由控制报文数同接收的数据报文数之比。该指标反映了网络的拥塞程度,较高的路由开销会阻碍网络中的关键数据传输,导致数据丢包或者平均延时增加。另外,卫星集群网络结构动态变化剧烈时,路由信息的维护开销会明显增加,致使数据传输出现局部拥塞。
卫星集群中参考卫星轨道参数见表1。仿真实验参考了卫星编队轨道设置[15],以表1中的2颗卫星为参考,用卫星集群生成模块在R=30 km的范围内随机生成额外14颗卫星,从而构建了包含16颗卫星的仿真场景。卫星集群仿真场景中包含8个通信对,均在仿真开始后100 s时依次发送数据。网络中每颗卫星的发射功率为30 dBm,传输速率为2 Mbit/s,天线模型为理想全向天线。卫星最大通信距离为10 km。网络中数据包生成模型采用CBR数据源,每个卫星节点生成速率为每秒4个数据包,单个数据包大小为512 B,队列缓存上限为50个数据包。考虑到卫星运动具有周期性,该卫星集群绕地球1圈的时间约为5 554 s,因此将仿真时间周期设为6 000 s,略长于卫星运行周期,以观察单个周期内的各路由算法随卫星相对运动引起的性能变化。仿真结果均为10次仿真结果的平均值。

表1 卫星集群中参考卫星轨道参数
3.2 仿真平台有效性验证
为确保卫星集群网络仿真平台数据来源的准确性,对卫星集群建模中自定义的卫星运动模块的精度进行验证。图4为所构建的卫星集群模型和卫星仿真软件STK在各方向位置上的结果对比。
由图4可见,单颗卫星在400 km轨道绕地球运行1圈后,各方向上的绝对位置偏差均不超过5 m,这表明基于NS-3软件构建的卫星集群运动模块与生成模块具有非常高的精度,能确保仿真过程中卫星运动数据的有效性。仿真结果还显示OLSR算法在网络拓扑变化剧烈时性能最稳定,同理论分析期望的结果一致。

图4 基于NS-3的卫星集群各方向上的 位置偏差(同STK比较)Fig.4 Position deviations in each direction of satellite cluster based on NS-3 (compared to STK)
3.3 结果分析
1) 卫星运动特性
卫星集群的运动特性直接影响到网络中路由算法的性能,所以本文对卫星集群的运动特性进行简要分析。图5为Sat2和Sat1之间相对位置和相对速度随时间变化趋势。图中,Sat2围绕Sat1在相对距离[6,23] km的范围运动,速度区间为[6.7,17.7] m/s,和地面无人机网络的相对运行速度相近[10],进一步说明卫星集群的网络性能分析可采用MANET路由算法进行参考。综合分析仿真中所有卫星的相对位置和相对速度可知,当卫星集群的分布范围在30 km3的运动空间时,星间相对运行速度在[0, 25] m/s区间变化。

图5 Sat2和Sat1之间相对位置和相对速度随时间变化趋势Fig.5 Trends of relative position and velocity from Sat2 to Sat1
由图5可知:当仿真时间约为1 000 s时,相对速度和相对位置的变化曲线的波峰和波谷相继出现,导致此时星间的相对角速度较大。考虑到实际中卫星天线的方向角,此时星间通信链路连接时间较短,性能降低;当仿真时间约为3 000 s时,星间相对角速度较小,但较大的星间距离会造成星间链路不稳定甚至断开,同样影响星间通信性能。因此,在实际设计路由算法时,搭建星间链路的时间窗口应尽量选择相对距离和相对速度均较小时,如图中[0, 1 000] s或[5 000, 6 000] s。
2) 路由协议性能分析
比较不同路由协议的分组交付率、平均时延和归一化路由开销随卫星集群网络拓扑变化的影响。网络中每个通信对的发包速率为4 Packet/s。
Sat9到Sat1的数据分组交付率随仿真时间的变化趋势如图6所示。由图可知,当仿真时间为[2 000, 3 000]s时,AODV和DSDV算法的分组交付率急剧减小,而OLSR算法变化较小。这是因为此时星间相对距离超过了最大星间通信距离,且卫星集群网络拓扑变化为非连通拓扑,使AODV和DSDV算法无法发现合适的路由路径,而OLSR算法具备链路状态感知特性,能及时发现不稳定的链路并切换,确保卫星集群网络通信的稳定。当仿真时间为[1 000, 2 000] s和[5 000, 6 000]s时,OLSR和DSDV算法的分组交付率略低于AODV算法,存在数据丢包。

图6 不同仿真时间区间内的分组交付率性能Fig.6 Performance of packet delivery rate in different simulation time intervals
图7为平均延时随仿真时间的变化趋势。由图7可知:3种路由算法的平均时延变化趋势同星间相对距离一致,OLSR算法在整个仿真过程中的平均时延最小,且时延抖动最小。当仿真时间在[1 000, 3 000] s时,2颗卫星相对距离增加,3种算法平均时延也相应增加,表明路由路径中的跳数在增加。但当OLSR算法的时延增加到90 ms时,开始呈下降趋势,而DSDV、AODV算法的时延则继续增大。当仿真时间在[2 000, 3 000] s时,由于拓扑动态变化加剧,DSDV算法需维护一些无用路由信息,致使此时的时延最高。当仿真时间在[3 000, 4 000] s时,网络连通性开始恢复,AODV算法的平均时延最高,这是因为AODV算法反应式的路由策略导致在网络拓扑更新后依旧使用时延较高的路由路径,可见其算法的滞后特性明显,不适用于拓扑构型急剧变化的卫星集群网络。
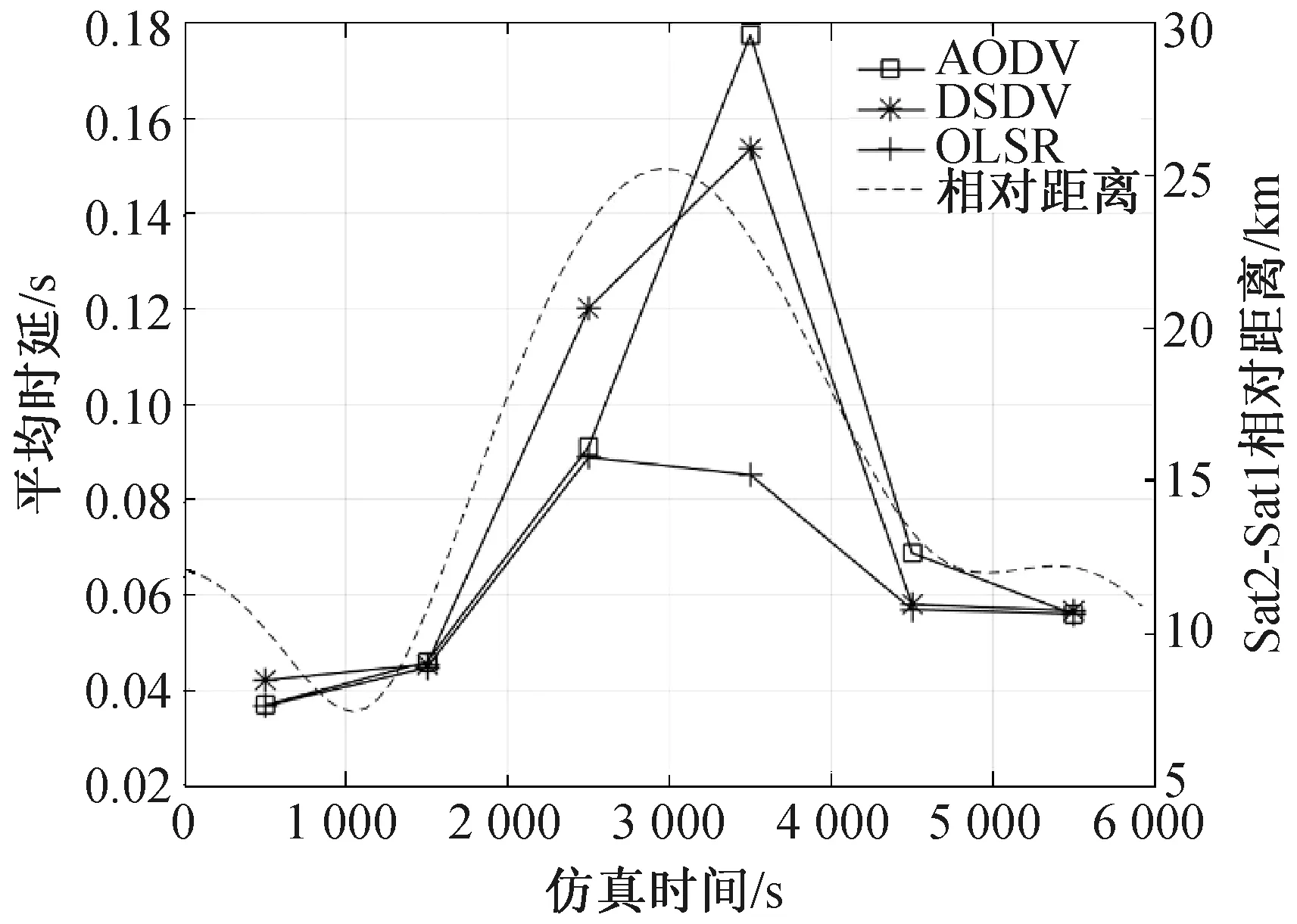
图7 不同仿真时间区间内的时延性能Fig.7 Performance of average delay in different simulation time intervals
图8为不同仿真时间区间内归一化路由开销随仿真时间的变化趋势。由图8可知,OLSR算法的归一化路由开销和相对距离波动变化均最小,AODV、DSDV算法在仿真中变化剧烈。这是由于OLSR算法的MPR分簇机制只需MPR节点周期性广播路由更新,从而当网络拓扑剧烈变化时,仍保持较低的路由开销。
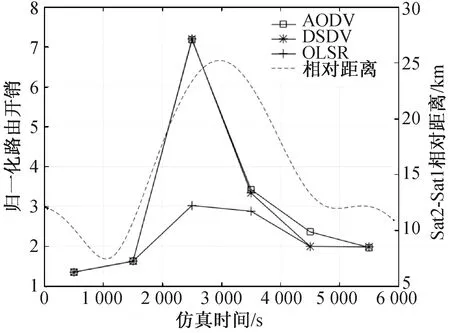
图8 不同仿真时间区间内的归一化路由开销性能Fig.8 Performance of normalized routing load in different simulation time intervals
从上述仿真结果可见:卫星集群网络拓扑的动态变化(星间相对距离的周期性变化)会严重影响部分路由算法的性能。AODV算法由于其反应式路由生成策略使其在卫星集群网络仿真中性能最差。OLSR算法在仿真中受拓扑变化的影响较小,其MPR分簇拓扑相较于AODV、DSDV算法的平面拓扑更能适应星间的周期性相对运动。OLSR算法的链路状态感知机制能及时发现网络中链路的变化,最快切换到稳定的路由路径,从而保证仿真过程中的分组交付率、时延、路由开销等性能。但OLSR算法在网络拓扑稳定时,存在数据丢包现象,这会影响星间协同任务的稳定执行,因此该算法需要优化以适用于卫星集群网络。
4 结束语
本文基于NS-3和STK软件搭建了卫星集群网络的综合性仿真平台,将AODV、DSDV和OLSR这3种路由算法应用在卫星集群网络中,从分组交付率、时延、归一化路由开销三方面分析了构建适用于卫星集群网络路由算法的思路。结果表明:具备链路状态感知和分簇机制的表驱动OLSR算法通过主动感知并切换通信链路,使其在3种路由算法中拥有最优的网络性能。因此,在研究适用于卫星集群网络的路由算法时,可参考OLSR算法中的MPR分簇和链路状态感知机制,同时将卫星相对运动预报模型和负载预测模型融入拓扑分簇和链路感知过程,使网络通信切换更稳定,确保星间协同工作时稳定与正确数据传输。为对卫星集群网络性能进行更准确的仿真。后续将完善基于NS-3和STK的卫星集群网络仿真平台,构建更合理的空间任务通信数据模型,完善星间通信协议模型,使其更符合星间通信的环境。
[1] 李德仁, 沈欣, 龚健雅, 等. 论我国空间信息网络的构建[J]. 武汉大学学报(信息科学版), 2015, 40(6): 711-715.
[2] 王敬超, 于全. 基于分布式星群的空间信息网络体系架构与关键技术[J]. 中兴通讯技术, 2016, 11(4): 9-13.
[3] 杨力, 李静森, 魏德宾, 等. 一种高动态卫星网络的拥塞控制算法[J]. 宇航学报, 2014, 35(8): 953-960.
[4] 方维维, 姚雪宁, 王文瑞, 等. 分布式星群网络中基于联系图的路由技术研究[J]. 北京交通大学学报, 2017, 11(5): 17-23.
[5] CHEN Q, ZHANG J, HU Z. A topology control strategy with reliability assurance for satellite cluster networks in earth observation [J]. Sensors, 2017, 17(3): 445.
[6] ZHANG W, ZHANG G, DONG F, et al. Capacity model and constraints analysis for integrated remote wireless sensor and satellite network in emergency scenarios [J]. Sensors, 2015, 15(12): 29036-29055.
[7] 陈菲, 路长厚, 潘伟, 等. 微型卫星集群系统协同任务下的目标分配研究[J]. 宇航学报, 2010, 31(5): 1374-1380.
[8] 党朝辉. 航天器集群边界建模与控制方法研究[D]. 长沙: 国防科学技术大学, 2015.
[9] 董云峰, 王兴龙. 卫星集群概念研究[J]. 航天器工程, 2012, 21(4): 83-88.
[10] 马林华, 张嵩, 茹乐, 等. 航空高动态网络链路感知OLSR路由算法[J]. 北京航空航天大学学报, 2016, 42(7): 1326-1334.
[11] 董思妤, 张洪, 王路. 无人机自组网OLSR路由协议的优化[J]. 军械工程学院学报, 2017, 29(2): 67-70.
[12] 王顶, 赵颐轩, 马娟. 无人机网络环境下AODV协议的优化[J]. 计算机测量与控制, 2013, 21(6): 1580-1583.
[13] 张禄林, 李承恕. MANET路由选择协议的比较分析研究[J]. 电子学报, 2000, 28(11): 88-91.
[14] WANG R, DAVE V, REN B, et al. Interplanetary overlay network (ion) for long-delay communications with asymmetric channel rates[C]//IEEE International Conference on Communications. IEEE, 2011: 1-5.
[15] 张志刚. 系绳式InSAR卫星系统动力学建模与展开控制研究[D]. 哈尔滨: 哈尔滨工业大学, 2016.

